Pure Mathematics
Vol.05 No.06(2015), Article ID:16327,7
pages
10.12677/PM.2015.56037
The Determination of the Number of Real Solutions of the Two Equations
Yanan Zhou
Yangtze College, East China Institute of Technology, Fuzhou Jiangxi
Received: Oct. 20th, 2015; accepted: Nov. 9th, 2015; published: Nov. 12th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, by determining the number of real solutions to the two equations, we can know that there is no real solution for the equations (1.a) in real numbers, and there are four solutions for the equation (1.b).
Keywords:New Elimination Method, The Number of Real Solutions of the Nonlinear Algebraic Equations

两个方程组实数解个数的判定
周亚南
东华理工大学长江学院,江西 抚州
收稿日期:2015年10月20日;录用日期:2015年11月9日;发布日期:2015年11月12日

摘 要
本文主要是对两个方程组的实数解的个数的判定,可知方程组(1.a)在实数范围内没有实数解,方程组(1.b)在实数范围内有四个解。
关键词 :新消元法,非线性代数方程组实数解组的个数

1. 介绍
寻找一元高次方程的求根公式是十八、十九世纪许多数学家的主要工作,为此付出辛勤努力的有卡尔达若、费拉里以及拉格朗日、阿贝尔和伽罗华等人,卡尔达若以三次方程求跟公式著名,以及后来的费拉里的四次方程的求根公式,随后人们在寻找五次及五次以上方程的求根公式,直到两个世纪后才有拉格朗日提出置换群(部分解决了一元高次方程问题),再随后阿贝尔给出了一元五次方程不可能有求跟公式的证明,最终由伽罗华创立的群论彻底解决了此问题,高于五次的一元高次方程没有求跟公式,从而引发了数学的一场革命性工作,开创了群论。由伽罗华理论我们可以知道非线性代数方程组同样不存在实根求解公式。一元高次方程的实数解个数的判定问题,早在19世纪初,数学家斯图姆就给出这一问题的解答,通常称为斯图姆定理。2014年初,周亚南在文献[1] 中给出了一种将多元高次方程组转变为一个一元高次方程式的新消元方法,在这里大胆猜想这个一元高次方程式的实数解的个数即为原方程组的实数解的个数。本文将通过文献[1] 中的消元法证明两个二元非线性代数方程组的实数解的个数,并证明二元高次方程组通过文献[1] 中的消元法后得到的一元高次方程组的实数解得个数即为原方程组的实数姐的个数。其中两个二元方程组如下:
 (1.a)
(1.a)
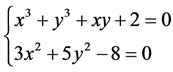 (1.b)
(1.b)
对比方程组(1.a)、(1.b),可知方程组(1.a)、(1.b)仅有一个符号上的区别,即方程组(1.a)中的数字8在方程组(1.b)中变为了-8。用上面的方法可知方程组(1.a)在实数范围内没有实数解组,而方程组(1.b)在实数范围内存在4组解。
2. 一些引理
引理1:如下的复数域内的一元高次多项式(2)
 (2)
(2)
在这里 角不能为零,不存在这样的实数
角不能为零,不存在这样的实数 ,
, (其中
(其中 ,
, 以及
以及 不全为零)满足方程组(2)
不全为零)满足方程组(2)
证明:当 时,可知方程式(2)变为下面的方程式:
时,可知方程式(2)变为下面的方程式:
 (3)
(3)
由于 角不能为零,
角不能为零, ,
,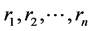 以及
以及 不全为零,故不存在实数
不全为零,故不存在实数 ,
, 以及
以及 角满足上面的式子(3)。同理,依次类推当
角满足上面的式子(3)。同理,依次类推当 时也不存在实数
时也不存在实数 ,
, 以及
以及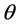 满足
满足 时的方程式等,依次类推可知引理1正确。
时的方程式等,依次类推可知引理1正确。
引理2:对于二元非线性代数方程组来说,假设其方程组的解有如下的结构
 (4)
(4)
则方程组的解有四种结构。
证明:当 时,可知方程组的解的情况如下
时,可知方程组的解的情况如下
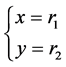 (4.1)
(4.1)
当 时,可知方程组的解的情况如下
时,可知方程组的解的情况如下
 (4.2)
(4.2)
当 时,可知方程组的解的情况如下
时,可知方程组的解的情况如下
 (4.3)
(4.3)
当 且其中一个为零时,可知方程组的解的情况如下
且其中一个为零时,可知方程组的解的情况如下
 或者
或者 (4.4)
(4.4)
从而证明了二元非线性方程组存在着四种结构,令 从(4.1)到(4.4)可知仅由(4.1)(4.2)满足
从(4.1)到(4.4)可知仅由(4.1)(4.2)满足 为实数,且由引理1可知,二元非线性代数方程组不存在(4.2)这样的解,故可知二元非线性代数方程组通过文献[1] 中的消元法消元后所得到的方程式的实数解的个数即为方程组的实数解的个数(把引理1,引理2进行推广是本文的后续工作)。这里有一个猜想:
为实数,且由引理1可知,二元非线性代数方程组不存在(4.2)这样的解,故可知二元非线性代数方程组通过文献[1] 中的消元法消元后所得到的方程式的实数解的个数即为方程组的实数解的个数(把引理1,引理2进行推广是本文的后续工作)。这里有一个猜想:
猜想1:所有的多元多次非线性代数方程组均不存在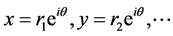 这样的解,其中
这样的解,其中 是实数且均不为零,且
是实数且均不为零,且 。
。
3. 方程组实数解个数的判定
3.1. 方程组(1.a)实数解个数的判定
首先对方程组(1.a)进行实数解个数的判定,为了能够很好的说明情况,我们在不引用引理1和引理2的情况下证明下面的命题时,即在引理1与引理2不成立的条件下去求解方程组(1.a)的实数解的个数,可知方程组(1.a)不存在实数解,其证法如下:
步骤1:第一步:令 ,并将其代入方程组(1.a)中可以得到下面的方程组
,并将其代入方程组(1.a)中可以得到下面的方程组
 (5)
(5)
将方程组(5)中的两个式子相除,可以得到下面的方程式(6)
 (6)
(6)
由方程组(6)可以得到下面的方程(4)
 (7)
(7)
由方程组(5)中的式子 可以得到下面的方程(8)
可以得到下面的方程(8)
 (8)
(8)
由方程式(7)、(8)可以得到下面的方程式(9)
 (9)
(9)
由方程式(9)可知不存在实数 ,使
,使 满足方程组(1.a)。
满足方程组(1.a)。
步骤2:第二步:令 ,应用新的消元法,即文献[1] 中的消元法将
,应用新的消元法,即文献[1] 中的消元法将 代入到方程组(1.a)中可以得到下面的方程组
代入到方程组(1.a)中可以得到下面的方程组
 (10)
(10)
用文献[1] 中的消元法(其过程略,详情文献[1] ),可以得到下面的一个方程式
 (11)
(11)
可知方程式(11)没有实数解,故可知方程组(1.a)没有实数解。对于多元非线性代数方程组当最终消元后得到的方程式有实数解时,在猜想1成立的条件下,方程式所得到的实数解的个数即为方程组的实数解的个数(在此可以用斯图姆定理进行求解)。
3.2. 方程组(1.b)实数解个数的判定
通过应用文献[1] 中的方法对方程组(1.b)进行消元后得到下面的方程式:
 (12)
(12)
由引理1和引理2可知方程式(12)的实数解的个数即为方程组(1.b)的实数解的个数,应用斯图姆定理构造斯图母序列或者应用Matlab对方程式(12)进行实数解个数的判定可知方程式(12)有四个实数解,本文后面附录一些程序目的为了验证此方法的合理性,通过附录6.2和附录6.3可以很好的验证此种方法的合理性。
4. 一些问题和猜想
问题2:是否可以将二元二次推广到二元多次,或者可以将二元二次推广到多元多次。
问题3:如果猜想1不正确是否可以对非线性代数方程组进行分类,如对二元多次的非线性代数方程组进行分类,或者以某种方法进行分类。
问题4:对文献[1] 中的算法进行算法复杂度方面的计算,并与现有的算法进行对比,如吴方法等进行对比,并说明其优缺点。
问题5:能否把文献[2] 中的方法推广到负数域内,这样可以扩大其数学的分支面,同样可以形成另一个数学分支。
问题6:可否对文献[1] 中的算法实现硬件方面和软件程序方面的应用,即可否实现一种应用方面的产品,如计算机什么的进行商业应用价值。
文章引用
周亚南. 两个方程组实数解个数的判定
The Determination of the Number of Real Solutions of the Two Equations[J]. 理论数学, 2015, 05(06): 259-265. http://dx.doi.org/10.12677/PM.2015.56037
参考文献 (References)
- 1. 周亚南. 非线性代数方程组的一种数值解法[J]. 应用数学进展, 2014, 3(2): 91-97. http://dx.doi.org/10.12677/AAM.2014.32014
- 2. 周亚南. 由一类对称非线性方程组的条件解所引发的理论[J]. 理论数学, 2014, 4(5): 179-196. http://dx.doi.org/10.12677/PM.2014.45027
附录
方程组(1.a)、(1.b)以及方程式(12)的解的情况(用Matlab实验所得)。
方程组(1.a)的Matlab实验数据
[x,y] = solve('x^3 + y^3 + x * y + 2 = 0','3 * x^2 + 5 * y^2 + 8 = 0')
x =
−1.0351956239716983230999345349078 − 1.0860797567679840078400005971515*i
0.57012563333777067911661184816044 + 1.1930730013057078478572981835961*i
0.76112262221287501240437531832626 + 1.0545936668206501167625078829654*i
0.57012563333777067911661184816044 − 1.1930730013057078478572981835961*i
−1.0351956239716983230999345349078 + 1.0860797567679840078400005971515*i
0.76112262221287501240437531832626 − 1.0545936668206501167625078829654*i
y =
0.50427347604380860022260324419036 − 1.3377324783897099964899871991625*i
0.39031529888074811678752393904095 − 1.0456185075575501098759552850326*i
−0.40116772229297776964170613059973 + 1.2005079957156981869312119384451*i
0.39031529888074811678752393904095 + 1.0456185075575501098759552850326*i
0.50427347604380860022260324419036 + 1.3377324783897099964899871991625*i
−0.40116772229297776964170613059973 − 1.2005079957156981869312119384451*i
方程组(1.b)的Matlab实验数据
[x,y] = solve('x^3 + y^3 + x * y + 2 = 0','3 * x^2 + 5 * y^2 – 8 = 0')
x =
−0.018557488306377930765383674844933
−1.3791854051715946272956791522842
0.67386847923004636710492632418466
−1.1789432646077132131965463352524
1.2474614710067670704973940506774 − 1.525282130199689092396405396633*i
1.2474614710067670704973940506774 + 1.525282130199689092396405396633*i
y =
−1.2648293844533559016406341800081
−0.6772802749947754224284529078064
−1.1521895519488582572935294768927
0.87524606100322696808352921280336
1.6029476278284602540079647285835 + 0.7122119238855857834077677169977*i
1.6029476278284602540079647285835 − 0.7122119238855857834077677169977*i
方程式(12)的Matlab实验数据
[k,y] = solve('−101 * k^6 + 72 * k^5 + 183 * k^4 – 16 * k^3 + 305 * k^2 + 200 * k−3 = 0','y = 0')
k =
2.0363584413885872284353601749585
0.014671930091502621724308510708936
−0.58485904345360447933030990356465
−1.3469849418760954992519728954924
0.29684245048916149985487141313045 − 1.0834395539835687600011836108365*i
0.29684245048916149985487141313045 + 1.0834395539835687600011836108365*i
y =
0
0
0
0
0
0