Pure Mathematics
Vol.06 No.02(2016), Article ID:17141,8
pages
10.12677/PM.2016.62014
Application of CVaR Metric in Extreme Value Theory
Jing Yao1, Yongming Li2
1Department of Mathematics, Guangxi Normal University, Nanning Guangxi
2Department of Mathematics, Shangrao Normal College, Shangrao Jiangxi

Received: Feb. 27th, 2016; accepted: Mar. 9th, 2016; published: Mar. 16th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Since the last half a century, with the globalization and diversification of economy, the financial risk measurement has gradually been concerned by the financial and economic scholars. After the 1990s, the new risk management tool, VaR (value at risk) measurement method has been developed gradually, which can measure risk value scientifically, accurately and comprehensively, and it is welcomed in the international financial community, but in extreme event, the accuracy of VaR is less than that of CVaR (conditional value at risk). This paper is intended to study the application of CVaR measure in extreme value theory.
Keywords:Extreme Value Theory, VaR, CVaR

CVaR度量在极值理论中的应用
姚竟1,李永明2
1广西师范学院数学科学学院,广西 南宁
2上饶师范学院数学系,江西 上饶

收稿日期:2016年2月27日;录用日期:2016年3月9日;发布日期:2016年3月16日

摘 要
近半个世纪以来,随着经济的全球化和多元化,金融风险的度量逐渐受到金融界以及经济学者的关注。90年代后,新型风险管理工具VaR(在险价值)测量方法逐步发展起来,以它能够科学、准确、综合的度量风险值而倍受国际金融界的青睐。但在极端事件发生期,VaR的度量准确性不如CVaR(条件在险价值)。本文意在研究CVaR度量在极值理论上的应用。
关键词 :极值理论,VaR,CVaR

1. 引言
本自20世纪70年代以来,金融市场的不稳定性日益明显,金融危机时有发生,例如1930年西方发生的经济大萧条及其金融危机、2008年9月15日爆发的并引发全球经济危机的金融危机等,这些事件给人类社会的发展和进步提出了严峻的考验。金融风险大小、风险评估以及风险控制等是金融工程中的重要研究课题。究竟应该如何度量金融风险的大小呢?风险价值是一种度量风险大小的工具,近年来受到国内外金融资产管理者的关注。如所周知,金融资产交易过程中呈现出显著的不确定性,金融资产的确定性关联失效。出现了金融资产收益序列的尖峰、厚尾现象,以及交易数据不确定。这种情况下VaR模型很难精准衡量风险值。VaR实质上是用收益分布的单一分位数表示,用以描述某一概率保证不超过它,但不能表示当超出VaR极端情况发生时期的期望损失程度。而CVaR(条件风险价值)却可以衡量,CVaR是一种一致性风险测度指标,在投资组合优化中有很大的应用潜能,但在金融领域内的实际应用研究尚未成熟。Tyrrel Rockafellar和Stanislav Uryasev在网上发布名为Optimization of Conditional Value-at-Risk的文章 [1] ,首先给出了条件风险价值CVaR对于组合优化的风险计量技术,在该篇文章里定义了CVaR的基本概念,即损失超出VaR条件期望。继该篇文章之后,Fredrik Andersson, Helmut Mausser等(2001) [2] 进一步讨论了CVaR的约束问题,探讨了信用风险优化问题。CVaR正处于研究的初期阶段,国内关于CVaR的研究才刚开始。国内早期更多的是对CVaR的理论综述。2008年后研究的学者增多,研究力度加强,成果日益丰硕。早几年代表的有陈剑利,李胜 [3] 在2004年给出CVaR风险度量模型在投资组合中的运用;曲圣宁,田新 [4] 研究了投资组合风险管理中的VaR模型的缺陷以及CVaR模型;霍玉琳,何春雄 [5] 研究了GARCH模型下的极值一致风险度量。随着经济发展,CVaR用于经济管理方面不断增加,有余星,孙红果,陈国华 [6] 探索了基于CVaR的融入期权的投资组合模型问题;黄鹂,魏岩 [7] 研究了基于CVaR模型投资组合保险的绩效实证等等。
极值理论(EVT)是处理与概率分布的中值相离极大的情况的理论,最早由提出Gumbel分布的Emil Julius Gumbel阐述。常用来分析概率罕见的情况,如百年一遇的地震、洪水等,在风险管理和可靠性研究中时常用到。本文结合极值理论和CVaR来研究金融市场的风险值。
2. 极值理论
预备知识
定义1:一致性风险测度的定义
θ为可测集,定义映射: ,
,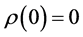 。当同时满足下面的条件时,
。当同时满足下面的条件时, 称为致性风险测度:
称为致性风险测度:
1) 单调性: ,
, ,
,
2) 次可加性:X,Y; ,
,
3) 正齐次性: ,
,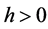 ,
, ,
,
4) 传递性: ,
, ,
,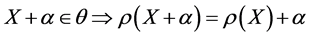 。
。
VaR不满足一致性测度公理的性质,CVaR和ES(Expected Shortfall)恰好能弥补VaR的不足。Acerbi (2002) [8] 给出当收益X的分布函数F(X)连续时,CVaR和ES等价。
设 表一资产在某整段时间内的n个时间段市场价格序列,定义
表一资产在某整段时间内的n个时间段市场价格序列,定义 为第t个时间段对数回报率。假设
为第t个时间段对数回报率。假设 是一个严平稳相依时间序列,其边际分布函数为
是一个严平稳相依时间序列,其边际分布函数为 ,给定
,给定 ,则在
,则在 置信水平下的VaR的值为:
置信水平下的VaR的值为:

定义VaR样本分位数估计为:

CVaR(损失超出VaR条件期望)值为:
 (1)
(1)
极值分布的理论统称为极值理论,主要研究随机样本和随机过程机制中的概率值和统计推断。用极值理论估计CVaR时,只需考虑对尾部的近似表达,更有效避开模型风险。本文用POT (Peaks over Threshold)模型估计CvaR。我们规定收益序列取的相反数(即加上负号)可转化为损失序列。
2.1. 极值分布
假设变量序列 ,是损失序列,分布函数为
,是损失序列,分布函数为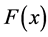 。Gumbel,Frechet,Weibull分布分别为极值渐近分布的三种表现形式,为方便统计应用,Jenkinson (1995)给出了广义极值分布模型,广义极值分布(GEV分布);
。Gumbel,Frechet,Weibull分布分别为极值渐近分布的三种表现形式,为方便统计应用,Jenkinson (1995)给出了广义极值分布模型,广义极值分布(GEV分布);
 (2)
(2)
其中 是形状参数,α是尾部参数,
是形状参数,α是尾部参数, 。当
。当 时,
时, 是Frechet分布;当
是Frechet分布;当 时,
时, 是Weibull分布;当
是Weibull分布;当 时,
时, 是Gumbel分布。我们主要研究Frechet分布。
是Gumbel分布。我们主要研究Frechet分布。
假设u为门限损失值,称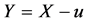 为超量损失,当Y > 0$的条件超限分布
为超量损失,当Y > 0$的条件超限分布 为:
为:
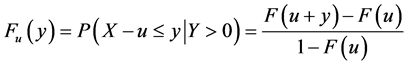
则有
 (3)
(3)
在1975年,Pickands首次介绍了广义Pareto分布,它含有两个参数 。GPD的分布函数为:
。GPD的分布函数为:
 (4)
(4)
其中 是尺度参数,
是尺度参数,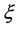 是形状参数。当
是形状参数。当 时,
时, ;当
;当 时,
时,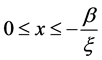 ,当
,当 时广义Pareto是厚尾分布。
时广义Pareto是厚尾分布。
2.2. 极值CVaR的计算
由Pickand提出当u足够大时,条件超限分布 近似于广义Pareto分布。即
近似于广义Pareto分布。即

构造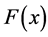 的尾部估计表达式:若
的尾部估计表达式:若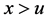 ,由(3)式可得:
,由(3)式可得:
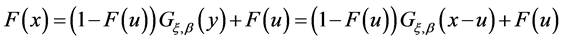 (5)
(5)
对 估计需要分以下几步进行:
估计需要分以下几步进行:
A1:找到合适的阈值u。
A2:估计广义Pareto分布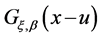 的参数
的参数 采用极大似然估计。
采用极大似然估计。
A3:估计 。
。
A4:估计尾部及分位数。
将A1~A4代入(5)得到 的尾部估计
的尾部估计
 (6)
(6)
其中 表示经验分布在u的取值,n为样本点总数,
表示经验分布在u的取值,n为样本点总数, 为样本中超出门限值得数目。
为样本中超出门限值得数目。 时,定义VaRp为在p的概率水平下的风险价值
时,定义VaRp为在p的概率水平下的风险价值

虽然VaR被广泛采用,但它不满足次可加性,且没有涉及到尾部风险的问题,然而CVaR恰好能够弥补这些缺陷。Acerb和Tasche给出了概率水平为 的ES积分表示方法:
的ES积分表示方法:

其中q(p)表示对应概率水平为p的分位数,他们还证明了在 连续的条件下ES和CVaR是等价的,故有:
连续的条件下ES和CVaR是等价的,故有:

3. 实证分析
本文意在研究恒生股指的风险和收益,我们收集了恒生指数的原始数据 ,
, 表示第t天的实数收盘价,我们定义每天对数收益率为:
表示第t天的实数收盘价,我们定义每天对数收益率为: ,数据样本从2006-01-04到2015-09-13 (数据来源:通信达),共2390个样本点,本文用R语言来实现GPD参数的极大似然估计和CVaR的计算。
,数据样本从2006-01-04到2015-09-13 (数据来源:通信达),共2390个样本点,本文用R语言来实现GPD参数的极大似然估计和CVaR的计算。
表1给出了样本数据的部分基本统计量,可知峰度(Kurtosis)大于3,即样本数据存在厚尾现象,偏度(Skewness)大于0表示图形右偏,即有右厚尾现象。即该时间段恒生股指的日对收益序列不服从正态分布,而是服从帕累托分布。
图1,图2分别为Hill图和QQ图,用于判断序列是否为正态分布,同时帮助确定阈值。
从图3~图5可以看出样本序列服从帕累托分布,其中图3经验分布函数图;图4简单均值剩余图,图形呈现向上的直线,说明有厚尾现象,且可知阈值在0.02左右以上;图5估计极值指标。
图6和图7是两个GPD相关图形:图6估计GPD参数图,GPD有两个参数,其中分布的形状参数 都大于0,表示不同指数的左右胖尾程度是不同的。但
都大于0,表示不同指数的左右胖尾程度是不同的。但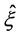 越大(
越大( ),尾部就越大,那么发生极端事件的概率就更大;图2是GPD高分位数尾估计图,表明该样本序列的GPD尾估计小于0.07。
),尾部就越大,那么发生极端事件的概率就更大;图2是GPD高分位数尾估计图,表明该样本序列的GPD尾估计小于0.07。
表2给出了同等条件下VaR度量风险的值和CVaR的度量值,从数值上对风险做出来客观的描述,CVaR值都比相应VaR值大,从简单的数字可以看出CVaR风险度量对于风险的描述更加准确。置信水平越小CVaR度量方法的优势越明显。综上可知,恒生股指序列存在尖峰厚尾现象,预度量该股的风险值,可用CVaR测度估计。
Table 1. Basic statistics
表1. 基本统计量

Figure 1. Hill diagram
图1. Hill图

Figure 2. QQ diagram
图2. QQ图

Figure 3. Empirical distribution function
图3. 经验分布函数图

Figure 4. Simple average remaining figure
图4. 简单均值剩余图

Figure 5. Estimate extreme value index
图5. 估计极值指标
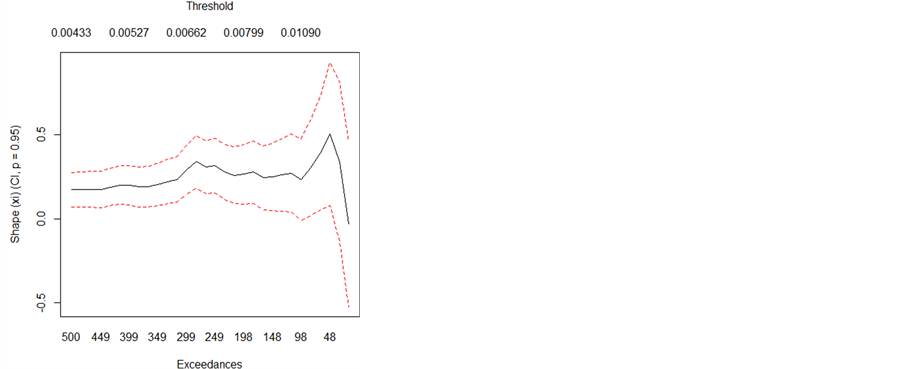
Figure 6. Parameters estimated GDP figure
图6. 估计GPD参数图

Figure 7. GDP higher median estimated figure
图7. GPD高分位数尾估计图
Table 2. Risk measurement
表2. 风险度量值
4. 总结
本文在研究超限分布为GPD分布时,利用极值理论并结合R语言,选择恒生股指2390个样本点作
为研究的对象,之所以选择恒生股指,一是它从1994年至今能够反映股票的性质,二是其他学者大多数研究上证或沪深,而笔者又想知道其他的股票是不是也能试用。极值理论是描述经验分布尾部的一个工具,不需拟合整个序列的分布,其基础理论是基于次序统计量的渐近分布理论。金融市场的极端现象频繁发生,用极值理论分析金融市场的波动和度量其风险是一个发展必然趋势。分析数据是否存在尖峰厚尾现象,采用极值理论估计CVaR的值不需要对整体分布建模,仅需考虑对尾部的分析表达,计算出CVaR的值。这是极值方法的优势,如果用正态分布或者其他分布,那序列分布的尾部难以拟合的好,那对风险的评估就存在极大的误差。极值理论在尖峰厚尾情况下估计CVaR的优点,使得极值理论近年得到了广泛的应用,其在金融风险管理中的前景也是不可估量的。
文章引用
姚 竟,李永明. CVaR度量在极值理论中的应用
Application of CVaR Metric in Extreme Value Theory[J]. 理论数学, 2016, 06(02): 95-102. http://dx.doi.org/10.12677/PM.2016.62014
参考文献 (References)
- 1. Rockafellar, T. and Uryasev, S. (2000) Optimization of Conditional Value-at-Risk. Jouranl of Risk, 2, 21-41.
- 2. Andersson, F., Mausser, H., Rosen, D. and Uryasev, S. (2001) Credit Risk Optimization with Conditional Value-at- Risk Criterion. Mathematical Programming, 89, 273-291. http://dx.doi.org/10.1007/PL00011399
- 3. 陈剑利, 李胜. CVaR风险度量模型在投资组合中的运用[J]. 运筹与管理, 2004(1): 95-99.
- 4. 曲圣宁, 田新. 投资组合风险管理中的VaR模型的缺陷以及CVaR模型[J]. 统计与决策, 2005(10): 18-20.
- 5. 霍玉琳, 何春雄. 研究了GARCH模型下的极值一致风险度量[J]. 金融经济, 2006(2): 152-154.
- 6. 余星, 孙红果, 陈国华. 基于CVaR的融入期权的投资组合模型[J]. 数学的实践与认识, 2014(1): 11-14.
- 7. 黄鹂, 魏岩. 基于CVaR模型投资组合保险的绩效实证[J]. 金融理论与实践, 2015(4): 98-103.
- 8. Acerbi, C. and Tasche, D. (2002) On the Cohe-rence of Expected Shortfall. Journal of Banking and Finance, 26, 1487- 1503. http://dx.doi.org/10.1016/S0378-4266(02)00283-2
