Modern Physics
Vol.4 No.05(2014), Article
ID:14061,4
pages
DOI:10.12677/MP.2014.45011
Chaos Structured by First Order Differential Circuit
1Electrical Engineering School of Guangxi University, Nanning
2Dongguan University of Technology, Dongguan
Email: *gxuhbh@163.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Aug. 1st, 2014; revised: Aug. 13th, 2014; accepted: Aug. 19th, 2014
ABSTRACT
Chaos is the most universally common form of bounded nonlinear function. It commonly exists in the various subject areas of nature. Chaos is the universal term of variously bounded nonlinear aperiodic oscillation. This paper proves that the first order differential circuit which is constituted by mixing of three harmonic sources with different frequency also can produce chaos. It sufficiently explains that the extensiveness of chaotic functions exists in nature. The main harmonic components in the differential equations can be solved by using the harmonic balance principle and power balance theorem. Their correctness of solving results can be verified by phase portrait plotted by simulation. In last century, the era when chaos theory was first published, chaos was considered as a singular attractor in a lot of literatures. The recognition is obviously unilateral and wrong. In fact, people can also make a completely opposite conclusion, the motional trajectory of phase point will neither diverge to be infinite nor converge to stable limit cycle. The phase point freely and arbitrarily wandering in phase space is ordinary and universal motional form, but it is non-random. Chaotic phase portraits on which trajectories are not repeated are pervasive phenomenon. The constant periodic oscillation which continuously repeats original orbit is an individual and special motion form.
Keywords:Chaos, Frequency Domain, Power Balance, Nonlinear Coupling, Harmonic, Phase Portrait

一阶微分电路构成的混沌
黄炳华1*,刘慧杰2,梁永清1
1广西大学电气工程学院,南宁
2东莞理工学院,东莞
Email: *gxuhbh@163.com
收稿日期:2014年8月1日;修回日期:2014年8月13日;录用日期:2014年8月19日

摘 要
混沌是有界非线性函数最一般的普遍形式,它普遍的存在于自然界的各个学科领域。混沌是各种各样有界非线性振荡的统一术语。本文证明三个频率不同谐波源混频构成的一阶微分电路,也可以产生混沌。它充分说明混沌函数存在的广泛性。该微分方程能够用谐波分析法和功率平衡定理求出它的主谐波解。并用仿真软件画出相图,验证求解结果的正确性。在上世纪混沌理论刚刚出现时,很多文献认为是奇异吸引子,这种认识显然是片面的。事实上,人们也可以做出一个完全相反的结论,相点的运动轨道既不发散趋于无穷,也不收敛为稳定极限环。相点自由任意的游荡在相空间不是随机的,是正常一般的运动形式。轨线不重复的混沌相图是无处不在的普遍现象,轨线不断重复的等周期振荡才是特殊的个别现象。
关键词
混沌,频域,功率平衡,非线性耦合,谐波,相图

1. 引言
在混沌理论诞生前,除了直流电源以外,人类无法构造一个非周期的激励源,因而习惯的将周期函数视为普遍性的函数,非线性系统出现的极限环是一个闭轨,相点的运动始终在这个轨道上不断重复,似乎是非常完美的动态形式,一旦离开这个完美的图像,就被人类认为是奇异的,这种认识显然是很值得商酌的。难道自然界物体运动,或电荷运动表现为电压电流变化的时间过程,都要那么完美才是正常普遍的吗?事实上,相轨线不重复的相图,应该是自然界的普遍普通现象,完美的闭合周期轨是特殊的个别现象。
当今很多文献,一旦提出新的混沌系统,就要用散度为负论证混沌吸引子的存在[1] -[6] 。其实如果吸引子存在散度必为负,但散度为负吸引子未必存在。用功率平衡理论分析非线性电路与混沌,为研究非线性振荡开辟了另一个途径,而混沌是非线性振荡的普遍形式。
本文介绍包含有三个频率不同激励源的混频电路,构成一阶微分方程,网络中只有耗能的正性电阻,不能诞生自激振荡。用频域平衡定理与电路定律求出三个主谐波,在相互耦合的情况下,证明每一频率成份的复功率各自守恒。并用谐波分析法印证求解结果的正确性。在一定的仿真时间内仿真相图是混沌解。画出的相图验证主谐波解是数值仿真解的主体基本部份。又印证了频域功率平衡定理的正确性[7] -[14] 。
自然界的振荡解包含两种类型,一类是周期性信号,如果一个信号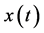 ,对任意的
,对任意的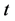 存在有一个非零正值
存在有一个非零正值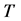 使(1)成立,式中
使(1)成立,式中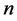 为正整数,则
为正整数,则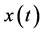 是周期性信号。
是周期性信号。
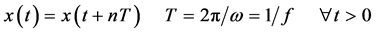 (1)
(1)
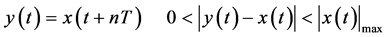 (2)
(2)
另类是非周期振荡性信号,这类信号虽然不满足(1),但有持续振荡特性,而不是单调变化的。动态变量反复振荡变化,在相图表现为相点在有限范围内游荡,而其轨线永不重复,或者说在仿真时间内,相点的循环轨道始终不重复。它满足(2),即经过一定间隔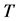 后,函数值不等于原来的
后,函数值不等于原来的 而是
而是 ,两者之差的绝对值小于信号绝对值的最大值
,两者之差的绝对值小于信号绝对值的最大值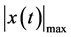 。式(2)是对持续非周期振荡一个初步,粗略,大体的定义,其含意是如果坐标原点是不稳定平衡点,相点围绕原点不停的游荡,而游荡的轨线又不重复。在经过一个间隔
。式(2)是对持续非周期振荡一个初步,粗略,大体的定义,其含意是如果坐标原点是不稳定平衡点,相点围绕原点不停的游荡,而游荡的轨线又不重复。在经过一个间隔 后,质点或电荷的运动形式不会那么完美的重复原来的过程,它的瞬时值
后,质点或电荷的运动形式不会那么完美的重复原来的过程,它的瞬时值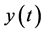 会在原来值
会在原来值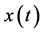 的上下波动,其波动量
的上下波动,其波动量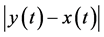 小于
小于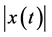 的最大值,保持持续振荡的特性。
的最大值,保持持续振荡的特性。
存在于自然界各学科领域动态变量 的变化规律,在线性系统大多是周期性的。在电路领域里,在科学技术历史的长河中,习惯的将周期函数视为普遍性的函数,即使在非线性电路中,人类也只能探索,研究,定性分析出现周期轨的相图,例如极限环,哈密顿环等。在这种习惯的支配下,人类长期以来认为周期函数是动态变量的普遍性函数。一旦在仿真时间内出现非周期解,就认为奇异,在上世纪中叶混沌现象的出现,就被认为是奇异吸引子,这是对自然界客观真理认识的颠倒。人类认识自然的过程,总是由简单到复杂。例如首先认识线性而后认识非线性。首先认识周期性而后认识非周期性。本文例证说明,动态变量的变化过程,在仿真时间内没有周期性,但有持续的振荡特性,满足式(2)就是一个混沌函数。
的变化规律,在线性系统大多是周期性的。在电路领域里,在科学技术历史的长河中,习惯的将周期函数视为普遍性的函数,即使在非线性电路中,人类也只能探索,研究,定性分析出现周期轨的相图,例如极限环,哈密顿环等。在这种习惯的支配下,人类长期以来认为周期函数是动态变量的普遍性函数。一旦在仿真时间内出现非周期解,就认为奇异,在上世纪中叶混沌现象的出现,就被认为是奇异吸引子,这是对自然界客观真理认识的颠倒。人类认识自然的过程,总是由简单到复杂。例如首先认识线性而后认识非线性。首先认识周期性而后认识非周期性。本文例证说明,动态变量的变化过程,在仿真时间内没有周期性,但有持续的振荡特性,满足式(2)就是一个混沌函数。
非线性振荡有周期态与混沌态之分。但用数值仿真画出相图时,因为处理的全部是有理数,因而严格的说,全部是周期解。如果所取仿真时间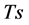 大于振荡周期
大于振荡周期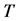 ,振荡表现为周期态;如果
,振荡表现为周期态;如果 ,在
,在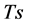 时间内显示是非周期的。混沌事实上是具有充分或无限长的振荡周期
时间内显示是非周期的。混沌事实上是具有充分或无限长的振荡周期 。是一个很普通的有界非线性函数,混沌是人类认识自然的又一次飞跃。历史上很早以前,人类就已经发现自然界存在寄生振荡的现象,显示屏上一片混乱。究竟是周期振荡或者是混沌振荡,恐怕是很难分清的。
。是一个很普通的有界非线性函数,混沌是人类认识自然的又一次飞跃。历史上很早以前,人类就已经发现自然界存在寄生振荡的现象,显示屏上一片混乱。究竟是周期振荡或者是混沌振荡,恐怕是很难分清的。
2. 用相量法求多谐波成份的耦合解
本文使用的符号说明如下:用下标 表示相量,下标
表示相量,下标 表示幅值,
表示幅值, 表示实部
表示实部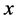 表示虚部,文中的虚数单位采用电工学的符号
表示虚部,文中的虚数单位采用电工学的符号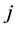 ,角频率记为
,角频率记为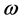 或
或 。以变量
。以变量 为例,
为例, 表示
表示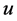 的
的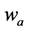 谐波分量的瞬时值,
谐波分量的瞬时值,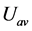 表示
表示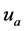 的相量值,
的相量值, 表示幅值;又如非线性支路电流用
表示幅值;又如非线性支路电流用 表示瞬时值,
表示瞬时值,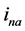 表示
表示 的
的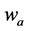 谐波分量,
谐波分量,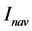 表示
表示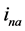 的相量,
的相量,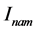 表示幅值,
表示幅值,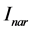 表示实功成份,
表示实功成份,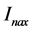 表示虚功成份,各值关系如式(3)。
表示虚功成份,各值关系如式(3)。
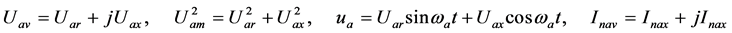 (3)
(3)
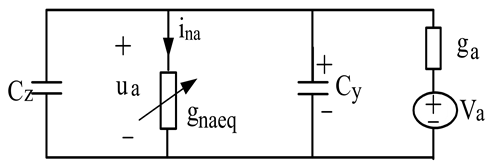
例1电路如图1,图中包含三个频率不同谐波源,画出三个分部网络如图2,其中图2(a)表示仅含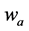 谐波的分部网络;图2(b)表示仅含
谐波的分部网络;图2(b)表示仅含 谐波的分部网络;图2(c)表示仅含
谐波的分部网络;图2(c)表示仅含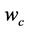 谐波的分部网络。但三个谐波相互之间有非线性耦合,表现在
谐波的分部网络。但三个谐波相互之间有非线性耦合,表现在 谐波的分部网络的
谐波的分部网络的 包含有另两个谐波电压
包含有另两个谐波电压 的贡献,余类推。也就是说三个分部网络不能独立求解后迭加;而必须共同联合求耦合解。
的贡献,余类推。也就是说三个分部网络不能独立求解后迭加;而必须共同联合求耦合解。
2.1. 非线性支路的耦合关系
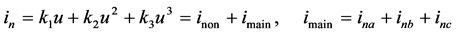 (4)
(4)
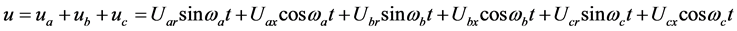 (5)
(5)
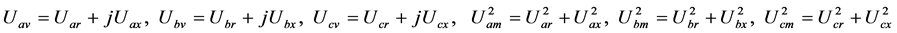 (6)
(6)
压控非线性电导 的伏安关系如式(4),设
的伏安关系如式(4),设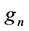 的控制电压包含
的控制电压包含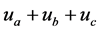 三个主谐波,其瞬时值如式(5),相量值和幅值如式(6)。以(5)代入(4),可得出
三个主谐波,其瞬时值如式(5),相量值和幅值如式(6)。以(5)代入(4),可得出 包含有众多谐波,其中
包含有众多谐波,其中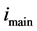 代表主谐波,
代表主谐波,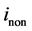 代表非主谐波。
代表非主谐波。
 (7a)
(7a)
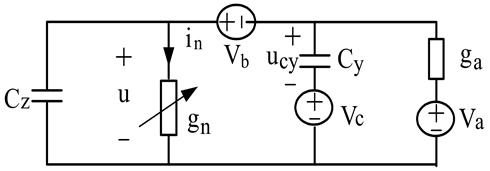
Figure 1. Mixing circuit
图1. 混频电路
 (a)
(a) (b)
(b) (c)
(c)
Figure 2. (a) Only contain Va; (b) Only contain Vb; (c) Only contain Vc
图2. (a) 仅含Va;(b) 仅含Vb;(c) 仅含Vc
 (7b)
(7b)
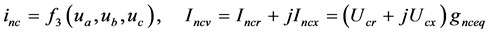 (7c)
(7c)
 (8a)
(8a)
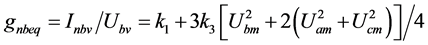 (8b)
(8b)
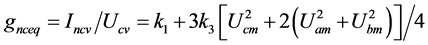 (8c)
(8c)
在本例证的计算中暂时忽略非主谐波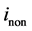 的影响,设
的影响,设 ,只考虑主谐波的计算。程序coupl.nb解出三个谐波电流
,只考虑主谐波的计算。程序coupl.nb解出三个谐波电流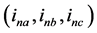 与三个谐波电压
与三个谐波电压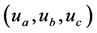 的关系如式(7)。
的关系如式(7)。
三个主谐波的电流相量与同谐波电压相量同相位,其中比值 ,
,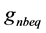 ,
, 称等效基波电导是实常数如式(7)和(8),它体现了三个分部网络是相互耦合关联的,不是分成相互无关的三个孤立部分。
称等效基波电导是实常数如式(7)和(8),它体现了三个分部网络是相互耦合关联的,不是分成相互无关的三个孤立部分。
2.2. 用相量法求三个主谐波
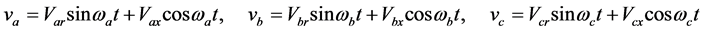 (9a)
(9a)
 (9b)
(9b)
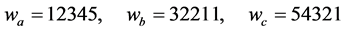 (10a)
(10a)
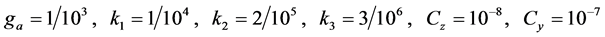 (10b)
(10b)
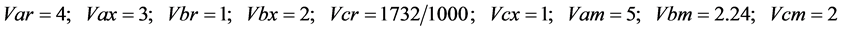 (10c)
(10c)
 (11a)
(11a)
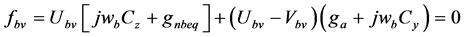 (11b)
(11b)
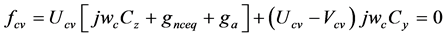 (11c)
(11c)
三个激励源的瞬时值,相量值与幅值如式(9);各元件的参数如式(10),用相量法列出三个分部网络图2(a)~(c)节点电压 的三个电流平衡方程如式(11)。其求解变量是相量
的三个电流平衡方程如式(11)。其求解变量是相量 ,
,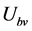 ,
,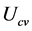 包含有六个未知实数,三个方程的实部与虚部必须各自等于零,因而可以建立6个实数平衡等式,解出6个未知实数,程序phase.nb解出的结果列如表1。
包含有六个未知实数,三个方程的实部与虚部必须各自等于零,因而可以建立6个实数平衡等式,解出6个未知实数,程序phase.nb解出的结果列如表1。
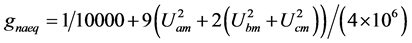 (12a)
(12a)
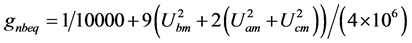 (12b)
(12b)
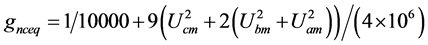 (12c)
(12c)
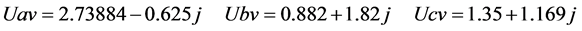 (13)
(13)
以Table 1/A的激励值为例,以式(10)的参数代入式(8)可求出式(12),以(6)与(12)代入(11),即可求出三个主谐波的相量值如式(13)。网络中电压电流相量值全部求出后,可用图2的三个分部网络,验证各支路的实功与虚功的总和各自为零。
表1. 例1的主谐波解
3. 用谐波分析法求主谐波解
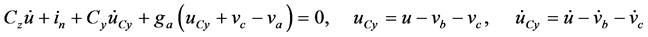 (14)
(14)
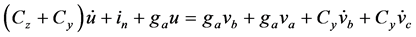 (15)
(15)
由电路图1的KCL与KVL可列出(14)经整理得式(15),这是一阶微分方程,用谐波平衡原理求式(15)中的变量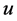 ,设
,设 包含谐波的主要成份如式(5),程序harmo.nb可求出三个主谐波的数据列如表1,和相量法程序phase.nb求出的结果是一致的。
包含谐波的主要成份如式(5),程序harmo.nb可求出三个主谐波的数据列如表1,和相量法程序phase.nb求出的结果是一致的。
电路图1表面上看起来,有两个电容 与
与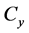 ,事实上只有一电容电压是独立状态变量,因为两个电容电压和两个电压源
,事实上只有一电容电压是独立状态变量,因为两个电容电压和两个电压源 形成回路。故最后形成一阶方程如式(15)。在图1,
形成回路。故最后形成一阶方程如式(15)。在图1,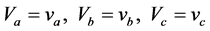 。
。
分析非线性方程(15)的解,可以参考参照线性理论,近代线性电路理论,将线性微分方程的完全解分成零输入解与零状态解。但比较经典的是分为齐次解与特解两部份,用这种分解方式类比式(15)会更合适,按这种分解方式,其中一部份是和起始状态有关的齐次解或称自由分量(或自然响应),这是令式右边激励源为零的解。另部份是方程的特解或称强迫解,它取决于方程右边的激励项,和起始状态无关,线性方程的完全解是两部份解的线性迭加。而非线性方程(15)的解应该是这两部份解的非线性耦合。
然而关于非线性方程自由分量的解析解是求不出来的,因为它是耦合解的一部份,显然不可能单独求出来。为了分析它的物理意义,我们令式(15)的右边激励项为零,得出式(16)并用数值仿真求出它的相图,显然是一条趋于零的渐近曲线如图3,式(16)对应于非线性的一维状态方程。
 (16)
(16)
谐波分析法和相量法只能求进入稳态的强迫响应,故求解的程序phase.nb与harmo.nb中不引入起始条件。图3的自由分量是无法用谐波分析法和相量法求出的。因为电路没有负阻没有自持的自激振荡,只有耗散的正性电阻,因而自由分量最终要衰减为零,故有时又称暂态响应,受迫解有时又称稳态响应。
以Table1/A的激励值为例。可做出下列三个稳态相图:作图语句做 万点,取最后的2%相点作为进入稳态的相图,显然到最后阶段自由分量或称暂态响应已完全消失,剩下的必然是稳态响应。
万点,取最后的2%相点作为进入稳态的相图,显然到最后阶段自由分量或称暂态响应已完全消失,剩下的必然是稳态响应。
① 激励源只保留 ;另两个激励源为
;另两个激励源为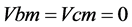 ;其
;其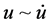 平面相图如图4,在一个激励源的驱动下,进入稳态的相图显然是一闭合的周期轨。本文相图3至相图14,横坐标表示
平面相图如图4,在一个激励源的驱动下,进入稳态的相图显然是一闭合的周期轨。本文相图3至相图14,横坐标表示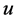 ,纵坐标表示
,纵坐标表示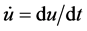 。
。
② 激励保留 ;
;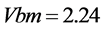 ;另
;另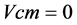 ;其
;其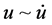 平面相图如图5,从直观而言已无法辩明相图是周期态或混沌态,有的文献称拟周期态。
平面相图如图5,从直观而言已无法辩明相图是周期态或混沌态,有的文献称拟周期态。
③ 三个激励源为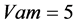 ;
;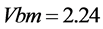 ;
;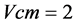 其
其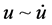 平面相图如图6,直观而言已很明显是一
平面相图如图6,直观而言已很明显是一

Figure 3. 
图3. 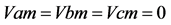
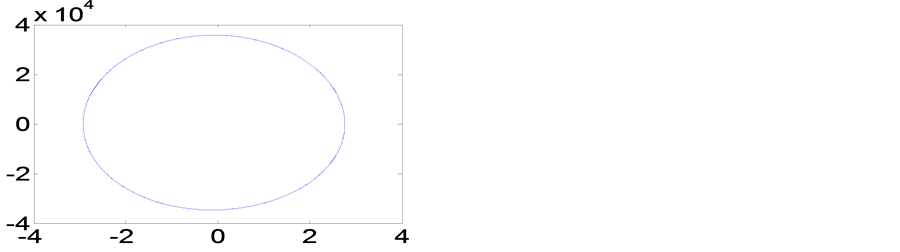
Figure 4.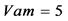 ,
, 
图4.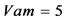 ,
,
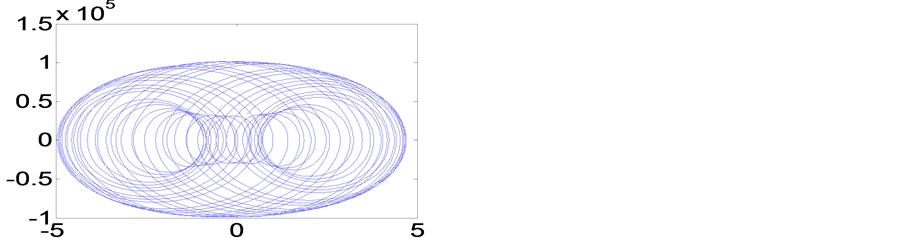
Figure 5.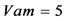 ,
, 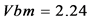 ,
, 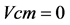
图5. ,
, ,
,

Figure 6.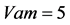 ,
,  ,
, 
图6.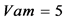 ,
, ,
,
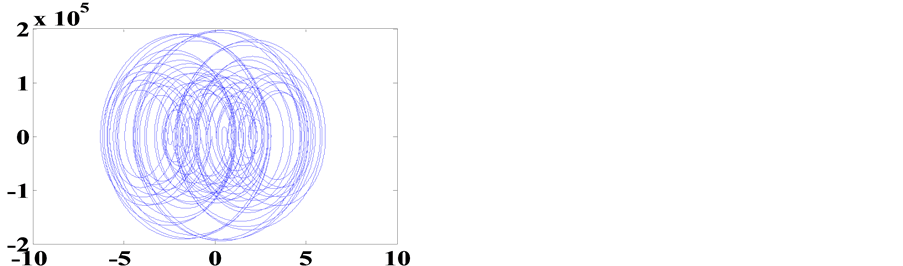
Figure 7. Plot (u(n96:n98), u1(n96:n98))
图7. 画96%至98%的相图

Figure 8. Plot (u(n96:n0), u1(n96:n0))
图8. 画96%至100%的相图

Figure 9. Phase portrait of Table 1/A
图9. 表1/A的相图
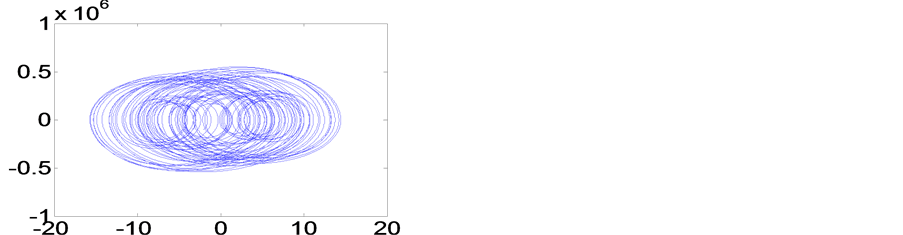
Figure 10. Phase portrait of Table 1/B
图10. 表1/B的相图
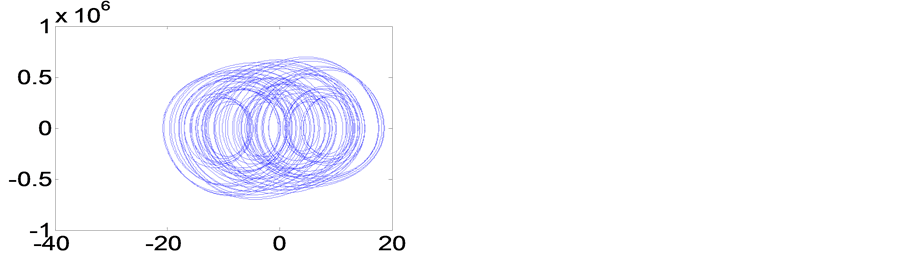
Figure 11. Phase portrait of Table 1/C
图11. 表1/C的相图
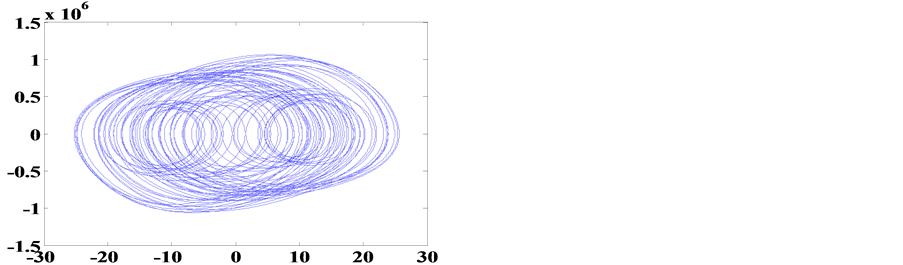
Figure 12. Phase portrait of Table 1/D
图12. 表1/D的相图
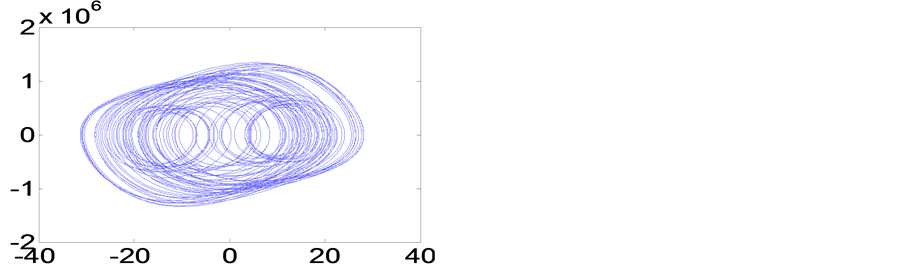
Figure 13. Phase portrait of Table 1/E
图13. 表1/E的相图

Figure 14. Phase portrait of Table 1/F
图14. 表1/F的相图
个混沌函数了,由此说明多谐波在非线性电路的混频会产生混沌。
为了追究为什么一阶非自治微分方程会诞生混沌?可以将式(15),化成不显含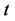 的自治方程。记
的自治方程。记 ,
,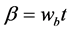 ,
,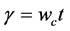 。图4对应的二维自治状态方程如式(17)。图5对应的自治三维状态方程如式(18)。图6对应的自治四维状态方程如式(19)。
。图4对应的二维自治状态方程如式(17)。图5对应的自治三维状态方程如式(18)。图6对应的自治四维状态方程如式(19)。
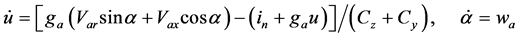 (17)
(17)
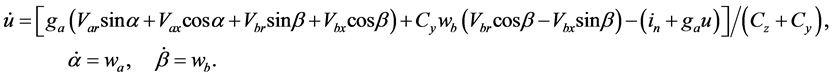 (18)
(18)
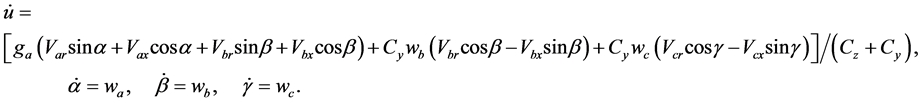 (19)
(19)
以上情况说明,用频域分析方法研究混沌可以得出有价值的结论,这是时域分析方法无法做到的。当加入混频的谐波成分越多,产生混沌的可能性越大,混沌的轨线越多越稠密,相图越复杂。直观判断相图的混沌态或周期态,是在定义一定仿真观察时间内判定的。当只有一个激励源驱动非线性电路时,不管非线性特性多么复杂,电路中诞生的各谐波必然是激励频率的整数倍,相图必然是一个闭合的周期轨,它的解可用Fourier级数表示。当两个激励源驱动非线性电路时,会产生混频与变频,相图是周期态或混沌态,从直观而言已分不清了,当三个激励源混合驱动时,直观观测已是很明显的混沌态了。
4. 用仿真相图求证一阶微分电路的混沌态
此处说的混沌态指的是在一定有限观察仿真时间内,相图是非周期的。
4.1. 画 万点的最后阶段并没有完成一个周期
万点的最后阶段并没有完成一个周期
以Table 1/A的激励值为例。取零起始状态,作图语句做 万点,取最后的96%至98%相点画相图7。再取最后的96%至100%相点画相图8。可以发现后者相图的相轨线比前者稠密得多,从98%到100%相点的阶段,轨线并没有重复而仍在增加。说明画到400万点的最后阶段并没有完成一个周期,是混沌的。
万点,取最后的96%至98%相点画相图7。再取最后的96%至100%相点画相图8。可以发现后者相图的相轨线比前者稠密得多,从98%到100%相点的阶段,轨线并没有重复而仍在增加。说明画到400万点的最后阶段并没有完成一个周期,是混沌的。
4.2. 取最后的98%至100%相点画表1各数据的全部相图
取起始状态为零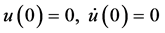 ,画最后的98%至100%相点的相图;然后再取起始状态为非零
,画最后的98%至100%相点的相图;然后再取起始状态为非零 ,也画最后的98%至100%相点的相图,可以发现两者是完全相同的。图9~图14横坐标的最大值,与表1的maxu是相当接近的,说明用相量法或谐波平衡法求出的主谐波解,能近似代表数值仿真解的主体基本部份。图6与图9相同。
,也画最后的98%至100%相点的相图,可以发现两者是完全相同的。图9~图14横坐标的最大值,与表1的maxu是相当接近的,说明用相量法或谐波平衡法求出的主谐波解,能近似代表数值仿真解的主体基本部份。图6与图9相同。
4.3. 取最后98%至100%相点画表1/A的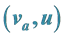 与
与 的相图
的相图
在三个激励源的共同驱动下,随着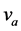 的变化,另两个因变量
的变化,另两个因变量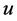 与
与 的变化情况如图15与图16,式(15)包含的三个激励源是已知的动态量(不是因变量是已知量),如果以
的变化情况如图15与图16,式(15)包含的三个激励源是已知的动态量(不是因变量是已知量),如果以 组成一个三维的相空间,也可画出一条空间曲线
组成一个三维的相空间,也可画出一条空间曲线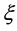 ,其参数式如(20),当
,其参数式如(20),当 时
时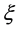 是有界的,它的变化规律受式(15)的约束。激励源
是有界的,它的变化规律受式(15)的约束。激励源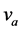 幅值5伏是不变的,当动态量
幅值5伏是不变的,当动态量 在±5伏范围内变化时,空间曲线
在±5伏范围内变化时,空间曲线 显示另两个因变量
显示另两个因变量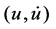 的变化情况。
的变化情况。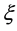 在三个平面的投影如相图9,图15,图16。同理也可画出随着
在三个平面的投影如相图9,图15,图16。同理也可画出随着 在±2,24伏的范围内变化,或
在±2,24伏的范围内变化,或 在±2伏的范围内变化,另两个因变量
在±2伏的范围内变化,另两个因变量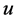 与
与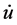 的变化情况,并用
的变化情况,并用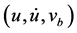 或
或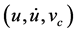 组成另两个三维的相空间,画出另两条空间曲线。
组成另两个三维的相空间,画出另两条空间曲线。
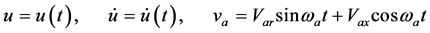 (20)
(20)
和典型的三维连续混沌系统如Lorenz方程或蔡氏电路比较,描写这两个动态系统的微分方程如式(21),其解析解如式(22)是一条空间曲线的参数式,无法求出它的具体形式。当今可以用数值仿真画出其相图,这就是混沌,它是三个动态变量相互关系的非线性函数。有一些能写出具体表达式被收入数学手册的空间曲线,是三变量函数的特殊形式,其空间图形有较明显的规律。恰恰是写不出表达式的混沌函数,才是三变量函数的普遍形式。其空间曲线的变化并非随机无规律的,这条空间曲线的变化规律受式

Figure 15. Plot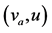 of Table 1/A
of Table 1/A
图15. 表1/A的 相图
相图
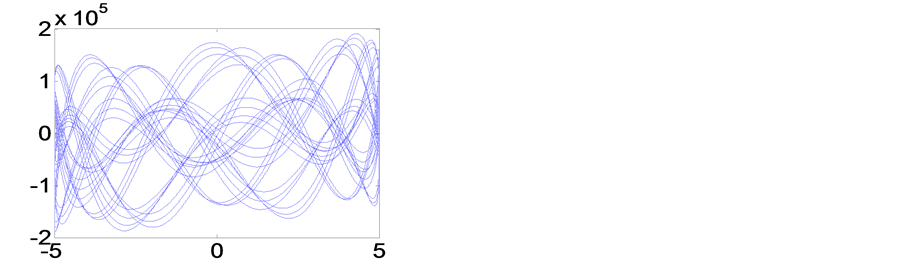
Figure 16. Plot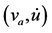 of Table 1/A
of Table 1/A
图16. 表1/A的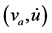 相图
相图
(21)的约束。此处用三维直角坐标的空间曲线表示三个动态变量的相互函数关系,其有关的定义,概念,推理和结论可以推广到多维的欧氏空间。
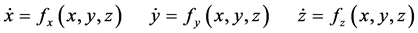 (21)
(21)
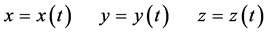 (22)
(22)
非线性动态系统的解,传统习惯于用时间函数 表示
表示 随时间
随时间 的变化过程,但这不是唯一的方式,特别是当
的变化过程,但这不是唯一的方式,特别是当 的表达式解不出来的时候。近代的电路与系统理论,也可以用相图来显示两个动态变量相互间的非线性函数关系,作为方程的求解结果。在两个变量构成的直角坐标相平面上,画出相点连续运动的相轨迹,也就是两变量相互间的关系曲线。同理,也可在动态系统中,选取合适的三个动态变量组成一个三维的相空间,三个变量相互间的非线性函数关系,可以用一条空间曲线来描写,这就是三维的相图。对于
的表达式解不出来的时候。近代的电路与系统理论,也可以用相图来显示两个动态变量相互间的非线性函数关系,作为方程的求解结果。在两个变量构成的直角坐标相平面上,画出相点连续运动的相轨迹,也就是两变量相互间的关系曲线。同理,也可在动态系统中,选取合适的三个动态变量组成一个三维的相空间,三个变量相互间的非线性函数关系,可以用一条空间曲线来描写,这就是三维的相图。对于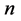 个变量可以组成
个变量可以组成 维相空间。
维相空间。
如果用替代变量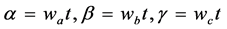 ,将式(15)化成二维,三维,四维的方程如式(17)(18)(19),则当
,将式(15)化成二维,三维,四维的方程如式(17)(18)(19),则当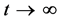 时,变量
时,变量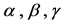 不是有界的,但
不是有界的,但 是有界的如相图4,图5,图6。做包含
是有界的如相图4,图5,图6。做包含 的相图,和画时间波形两者比较起来。例如画
的相图,和画时间波形两者比较起来。例如画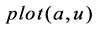 和画
和画 ,可以发现两者的纵轴均表示
,可以发现两者的纵轴均表示 ,说明波幅的变化两者是相同的,横轴
,说明波幅的变化两者是相同的,横轴 或
或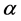 的尺度被展缩一个比例系数
的尺度被展缩一个比例系数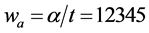 。纵轴的变化量相同,横轴的尺度被压缩一万倍的数量级,其轨线的密集度会使得显示范围一片兰色。因此要有一定作图技巧,才能显示出两个图是一致类似的。
。纵轴的变化量相同,横轴的尺度被压缩一万倍的数量级,其轨线的密集度会使得显示范围一片兰色。因此要有一定作图技巧,才能显示出两个图是一致类似的。
我们说混沌可以用一条三维(或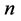 维的欧氏空间)有界空间曲线,来描写变量间的非线性函数关系。其中,动态变量是指含有界能源系统中的物理变量,在电路网络是指各种电变量,不包含
维的欧氏空间)有界空间曲线,来描写变量间的非线性函数关系。其中,动态变量是指含有界能源系统中的物理变量,在电路网络是指各种电变量,不包含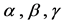 ,这三个数学上的替代变量,它不是系统的物理变量,它的物理意义是时间
,这三个数学上的替代变量,它不是系统的物理变量,它的物理意义是时间 的尺度展缩,当
的尺度展缩,当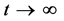 时,它显然不是有界的。
时,它显然不是有界的。
5. 关于混沌理论
大多数文献认为,混沌理论起源于1963年提出的Lorenz方程,随后研究混沌的文献不断拥现如雨后春笋,也有文献认为20世纪科学将永远铭记三件事相对论,量子力学与混沌,它在整个科学中的作用相当于微积分在18世纪对数理科学的影响,混沌和分形成为20世纪末21世纪初的学科前沿,它激起对非线性科学的广泛关注与研究[15] [16] 。此后,关于混沌的论述广泛出现在各个学科领域,但至今没有一个统一的定义,较著名的定义有李天岩–约克定理。各文献的介绍有共同共识的论点,也有分歧的论点见解不尽相同,混沌的性质多种多样更是各说不一,也有一本文献介绍多种定义的。并没有综合成一个常规完整的理论与统一严格的定义。
用频域的方法研究混沌是本文有价值的贡献,文中在例证电路图1的基础上,有以下几点结论与当前有些文献介绍的混沌理论是不同的。
① 不少文献认为混沌是奇异吸引子。我们认为相点运动轨迹的有界性不一定是吸引子,其相图的复杂性并不等于奇异,是很普通的自然现象。无损耗电路受外界因素干扰,使相点运动偏离原来的轨道,没有收敛的能力没有吸引性,此类混沌不是吸引子。从全局而言不会发散趋于无穷是有界的,从微小局部而言混沌轨线对邻近相点没有吸引性是不稳定的。诞生混沌的一阶微分电路图1,说明混沌态是普遍广泛存在的,周期态是个别特殊的,闭合周期轨的相图是混沌态的退化形式。
②用空间曲线描写混沌,事实上就是用相图显示系统中各量之间的函数关系,组成三维或n维空间的坐标变量,在电路网络中除了取状态变量(如例1中的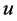 )外,还可取非状态变量(如例1中的
)外,还可取非状态变量(如例1中的 ),也可取系统中已知的动态量(如例1中的
),也可取系统中已知的动态量(如例1中的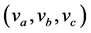 )。
)。
③ 有文献认为确定性系统可能诞生随机性结果,本文认为混沌是微分方程确定性的解。相图是根据微分方程理论画出来的,只要微分方程的理论没有被推倒,混沌函数可以用唯一的相图来描写的结论恒成立。一个微分方程包括起始条件,只对应一个相图。不可能有两个相图,因而混沌方程的解是唯一确定的。
④ 混沌的非周期性,这是当今学术界的共识,但要注明一点,按照数学理论的严格分析,只要是数值仿真,其处理的全部是有理数,因而其画出的仿真相图全部都是周期态,不过周期很长很长。在定义有限的观测时间内,画出的相图可以有周期态与非周期的混沌态之分。只要承认在仿真时间内的混沌是非周期的,那么随着仿真时间的延长,轨线会不断延长和增加而显得更加稠密,当空间曲线的平面投影相图,在轨线的充满性遍历性已达到不能分清线条的程度,混沌仍表现为还没有完成一个周期。反之,如果后面的轨线重复前面的轨道,就说明此后相点的运动会不断重复下去,不会有新增的轨线,不会更加稠密,相图最后进入周期轨。
⑤ 当今出现一些定名的混沌系统,如Chua’s电路,Lorenz系统,Chen,Lu,Liu,Qi系统,等等,似乎是有限的少数例证,这些例证为混沌理论的发展做出重要贡献,但不久的将来,千姿百态各种各样的混沌系统必然会大量涌现出来。混沌和求不出解析表达式的有界非线性非周期振荡,两者是同义语。
⑥对初值敏感依赖,并非混沌专有的特性,很多系统例如处于不稳定极限环的点集,对初值的依赖也非常敏感。数学上已经有 与
与 的定义,在0点左右都是极其敏感的,这种特性甚至于在线性系统也屡见不鲜。
的定义,在0点左右都是极其敏感的,这种特性甚至于在线性系统也屡见不鲜。
6. 结论
① 本文用频域分析方法,研究多谐波混频构成的一阶微分电路会得出混沌相图,这是与当今学术界所提出的各种混沌不同的新型混沌,可以形成一个新的混沌系统族。通过本文的研究,可以充分说明混沌函数存在的广泛性,决不是当前出现的几十个例子,只要将图1电路网络做各种各样的变化,例如将图中的两个电容改换成两个电感,或改换成一个电感一个电容,必然又是另一个混沌电路,改变图1的网络连接与增减元件,可以有各种各样无穷无尽的变化,随着混沌研究的不断深入与发展,其可以构造出的混沌相图不计其数,这已经是勿用置疑了。
② 这个电路网络的特点是具有多谐波源与正性非线性电阻,图4至图6的演化过程说明,随谐波源的增加,诞生混沌的可能越大,其前提是参与混频各谐波源的强度要相差不多。不能有其中一个激励源的幅值,远远超过其它激励幅值。
③ 表1数据全部相图的混沌态,说明要有足够的瞬时能量交换源,图1电路共有5个能量交换源,三个激励源和两个电容,电路中的五个元件,能量不断的吞吐相互交换是诞生混沌很重要的原因。这种元件起码要有三个或以上。无损耗电路的激励源不是一个能源,它不送出能量,它发挥的作用仅仅是一个能量交换源,它和电感电容共组成三个能量交换源,不断交换吞吐能量,故也能诞生混沌[17] [18] 。
④ 图1电路作为混沌信号发生器,有广泛的实际应用价值,在实验室实现起来,要比其他电路简单容易得多。例如用无损耗电路构造混沌信号发生器,要制作非线性电感[17] [18] 。用蔡氏电路要构造一个有负阻效应的非线性电导,它必须用有源器件实现。和这两种电路比较起来,电路图1有更加广泛的实用价值,除了一个正性的非线性电阻外,全部是线性元件,根据表1的数据,三个电压源的幅值在2~40伏之间,振荡频率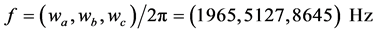 ,这在电子实验室是很容易实现的。正性非线性电阻的构造可以用无源元件实现,要比制作非线性电感容易得多。用一个混沌信号发生器(例如本文的电路图1或蔡氏电路或无损耗电路,视为一个非周期激励源),去驱动一个仅仅由非线性的L与C元件组成的非线性网络,其输出端必然又是另一个新型的混沌。这样一来混沌函数就包罗万象无处不在了。
,这在电子实验室是很容易实现的。正性非线性电阻的构造可以用无源元件实现,要比制作非线性电感容易得多。用一个混沌信号发生器(例如本文的电路图1或蔡氏电路或无损耗电路,视为一个非周期激励源),去驱动一个仅仅由非线性的L与C元件组成的非线性网络,其输出端必然又是另一个新型的混沌。这样一来混沌函数就包罗万象无处不在了。
基金项目
国家自然科学基金资助项目(No. 60662001)。
参考文献 (References)
- [1] 冯朝文, 蔡理, 康强, 张立森 (2011) 一种新的三维自治混沌系统. 物理学报, 3, Article ID: 030503.
- [2] 唐良端, 李静, 樊冰, 翟明岳 (2011) 新三维混沌系统及其电路仿真. 物理学报, 2, 785-793.
- [3] 许喆, 刘崇新, 杨韬 (2010) 一种新型混沌系统的分析及其电路实现. 物理学报, 1, 131-139
- [4] 王杰智, 陈增强, 袁著祉 (2006) 一个新混沌系统及其性质研究. 物理学报, 8, 3956-3963.
- [5] 刘凌, 苏燕辰, 刘崇新 (2006) 一个新混沌系统及其电路仿真实验. 物理学报, 8, 3933-3937
- [6] Yu, S.-M.,Qiu S.-S. and Lin, Q.-H. (2003) New results of study on generating multiple-scroll chaotic attractors. Science in China (Series F), 46, 104-115.
- [7] Huang, B.H., Li, G.M. and Liu, H.J. (2014) Power balance theorem of frequency domain and its application. Journal of Modern Physics, 5, 1097-1108.
- [8] 冯久超, 李广明 (2012) 功率平衡理论在研究非线性电路与混沌中的进展. 华南理工大学学报, 11, 13-18.
- [9] 黄炳华, 钮利荣, 蔺兰峰, 孙春妹 (2007) 功率平衡基础上的基波分析法. 电子学报, 10, 1994-1998.
- [10] 黄炳华, 黄新民, 韦善革 (2008) 用基波平衡原理分析非线性振荡与混沌. 通信学报, 1, 65-70.
- [11] 梁永清, 黄炳华 (2014) 非线性电路频域的功率平衡. 太原理工大学学报, 3, 328-333.
- [12] Huang, B.H., Huang, X.M. and Li, H. (2011) Main components of harmonic solutions of nonlinear oscillations. International Conference on Electric Information and Control Engineering, ICEICE, Wuhan, 15-17 April 2011, 2307-2310.
- [13] Huang, B.H., Huang, X.M. and Li, H. (2011) Main components of harmonic solutions of nonlinear oscillations. Procedia Engineering, 16, 325-332.
- [14] Huang, B.H., Yang, G.S., Wei, Y.F. and Huang, Y. (2013) Harmonic analysis method based on power balance. Applied Mechanics and Materials (Manufacturing Engineering and Process II), 325-326, 1508-1514.
- [15] 关新平, 等 (2002) 混沌控制及其在保密通信中的应用. 第1版, 国防工业出版社, 北京, 1-16.
- [16] 刘式达等 (2003) 自然科学中的混沌和分形. 第1版, 北京大学出版社, 北京, 1-32.
- [17] 黄炳华, 李广明, 卫雅芬 (2012) 用虚功平衡原理求解无损耗系统的主谐波. 现代物理, 3, 60-69.

NOTES
*通讯作者。
