Modern Physics
Vol.
11
No.
03
(
2021
), Article ID:
42466
,
11
pages
10.12677/MP.2021.113006
AlnPn (n = 2~9)团簇结构与性质的理论研究
彭从一1,马磊1*,马丽2,和一鸣1,王文杰1
1成都理工大学地球物理学院,四川 成都
2吉利学院汽车工程学院,四川 成都

收稿日期:2021年4月16日;录用日期:2021年5月14日;发布日期:2021年5月21日

摘要
团簇的结构和稳定性具有明显的尺寸效应,研究其性质有助于人们对物质有更深入的认识。通过结构搜索结合密度泛函方法,我们系统地研究了AlnPn (n = 2~9)团簇的结构、稳定性和电子性质。随着尺寸的增大,AlP团簇逐渐接近笼状结构,AlP团簇中Al原子和P原子之间交替成键,稳定性增强,Al原子和P原子间的相互作用逐渐减弱。能隙研究表明AlnPn (n = 2~9)团簇表现为半导体性质。Al-P原子之间的电荷转移比Al-Al和P-P间更强,表现出离子性质。成键分析表明,Al-P之间有较强的共价相互作用。
关键词
AlP团簇,密度泛函理论,结构与性质
Theoretical Study on the Structure and Properties of AlnPn (n = 2~9) Clusters
Congyi Peng1, Lei Ma1*, Li Ma2, Yiming He1, Wenjie Wang1
1Department of Geophysics, Chengdu University of Technology, Chengdu Sichuan
2College of Automotive Engineering, Geely University of China, Chengdu Sichuan
Received: Apr. 16th, 2021; accepted: May 14th, 2021; published: May 21st, 2021

ABSTRACT
The structure and stability of clusters have prominent size effects, and studying their properties is helpful for people to have a deeper understanding of matter. The structures, stability and electronic properties of AlnPn (n = 2~9) clusters were systematically studied by structure search based on density-functional theory. With the increase of the cluster size, the AlP clusters gradually approach the cage structures, the alternating bonding between Al and P atoms in AlP clusters, the stability of the clusters increases, and the interaction between Al and P atoms decreases. The AlnPn (n = 2~9) clusters exhibit semiconductor properties. The charge transfer between Al-P atoms is stronger than that between Al-Al and P-P atoms, showing ionic properties. Bonding analyses show that there is a strong covalent interaction between Al and P atoms.
Keywords:AlP Cluster, Density-Functional Theory, Structure and Properties

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
团簇作为原子和块体物质之间的桥梁,由于其新颖的结构、电子、光学和化学性质,已成为人们深入研究的对象 [1]。近年来,研究人员围绕团簇开展了大量的实验和理论研究,其中利用团簇不同于块体和分子的特殊性质而进行理论研究,并通过实验制备具有特殊功能性质的材料已成为研究的重要方向之一 [2] [3] [4]。团簇是由几个乃至数千个原子或分子通过一定的物理或化学作用力组成的相对稳定的聚集体,其物理和化学性质随团簇粒子数目的改变而变化 [1]。团簇的形状和对称性极度依赖原子的结合方式,而异构体的存在使团簇的研究变得更加复杂。因此,需要详细了解团簇的几何结构和电子结构,以便于能正确地解释实验中的问题。先前的研究已经讨论了团簇的各种性质,如团簇的尺寸、结构、成键和极化率等,从而得出一些重要的结论 [5]。半导体具有低密度、高熔点、大体积模量、良好的硬度、较宽禁带、耐腐蚀性和发光特性等独特的物理性质。III-V族半导体团簇的特殊光电性质使得其在材料科学领域具有广阔的应用价值,并有望作为构建单元,在制造新的纳米材料中发挥至关重要的作用 [6] [7]。和同族其它团簇相比,AlP团簇可以形成稳定的类富勒烯状结构,具有更高的振动频率和易于观察的光电子能谱 [8]。
目前有关AlP团簇的实验工作较少。Gomez等 [9] 和Huang [10] 发现了AlxPy负离子团簇的质谱峰,证明了铝磷二元团簇的存在。Liu等 [11] 以脉冲激光束真空溅射的方式产生了铝与磷的离子束,记录了二元铝磷团簇的离子质谱,表明正离子主要局限于仅包含一个铝的离子团簇,负离子的组成更加丰富,二元铝磷离子团簇中奇数磷离子团簇的稳定性远高于偶数磷离子团簇。而在理论研究方面,Al-Laham等 [12] 利用Hatree-Fock (HF)和Mӧller-Plesset微扰理论中的MP2方法确定了(AlP)n (n = 1~4)团簇的最低能量结构。Tomasulo等 [13] 则拓展研究了(AlP)n (n = 1~6),并证明其结构不同于Si2n团簇。Feng等 [14] [15] 研究了中性和带电的AlnPm (n + m ≤ 4)的几何结构和能量等性质。Archibong等 [16] [17] 在DFT和CCSD(T)水平上研究了 、 、 和 的几何结构、振动频率和电子剥离能, 最稳定的结构是C2v扭曲四面体而非平面结构, 的稳定构型为D3h。Costales [18] 研究了(AlP)n (n = 1~3)的结构和振动频率,(AlP)3表现出类似于氮化物的D3h结构。Qu和Bian [19] 则使用B3LYP/6-311 + G(d)方法研究了(AlP)n (n = 2~4)的结构、电子态和稳定性,对于二聚体和三聚体,最稳定的结构是具有Dnh对称性的环状,而四聚体中最稳定的构型具有Td对称性。Zhao等 [20] 使用密度泛函理论研究了AlnPn (n = 1~9)团簇的最稳定结构,在n ≥ 5时观察到具有Al-P交替排列的笼状结构,计算的结合能、HOMO-LUMO能隙、电子亲和势和光电子能谱与实验结果一致。Karamanis等 [21] 研究了AlnPn (n = 2~9)团簇的平均偶极化率和极化率各向异性,并使用不同方法计算极化率并进行了对比分析,结果表明AlP团簇的理论预测极化率大于块体极化率,且尺寸的增加是团簇向块体转变的必要不充分条件。在本文中,我们对AlnPn (n = 2~9)团簇进行了系统的搜索,并采用密度泛函方法详细地研究了AlP团簇的稳定性、电荷分布及电子局域函数,希望我们的研究对深入了解AlP团簇的性质及进一步的实验合成有所帮助。
2. 计算方法
寻找最稳定的低能异构体是团簇研究中重要的一部分。Molclus [22] 是一款操作简单,能够自动调用Gaussian、ORCA或MOPAC2012/2016程序来高效搜索团簇初始构型和分子构象的程序。与其它算法相比,Molclus程序具有更加简便、广泛采样势能面(PESs)的优点,并且不会落入PES的一个局域极值。genmer是生成团簇初始构型的工具,原理简述为让加入的单体团簇中心从体系的原点出发向着一个随机的方向“发射”,发射过程中单体不断移动,当这个单体被移动到和体系已有的原子没有不合理接触,这个单体就被加入当前团簇。本文首先基于Molclus程序中的genmer工具进行系统的结构搜索,输入原子类型和数目,随机生成众多初始结构的坐标文件,参数设置除了修改每次要产生的团簇总数以及Al与P的原子个数以外,其它参数经过反复尝试后均选用为默认值。随后调用Gaussian 09 [23] 软件中密度泛函理论的Becke三参数交换泛函和Lee-Yang-Parr关联泛函(B3LYP) [24] 进行几何优化和能量计算,基组为6-31 + g(d)。最后通过Molclus程序中isostat工具进行稳定结构去重、筛选、排序。我们计算了AlnPn (n = 2~9)结构的振动频率,以确保优化的团簇都无虚频。又采用MP2/6-31 + g(d) [25] [26] 方法比较了AlnPn (n = 2~9)团簇的稳定性。团簇的电子结构分析则通过Multiwfn [27] 程序实现。
3. 结果与讨论
3.1. AlnPn (n = 2~9)团簇的几何结构
采用B3LYP/6-31 + G(d)方法优化的AlnPn (n = 2~9)低能异构体如图1所示,括号中为异构体相对于最稳定结构的能量。AlnPn (n = 2~9)最低能量异构体与先前文献报道的结果一致 [12] [13] [18] [20] [21]。表1列出了Al-P团簇中最稳定异构体的平均键长。
Al2P2-a为具有D2h点群的菱形结构,其中Al-P键长为2.54 Å,P-P键长为2.08 Å。Al2P2-b是四面体结构,具有C2v对称性,其结构可看作由单独的Al2与P2组合而成,Al2P2-b的Al-P键键长长于Al2P2-a,
Table 1. Average bond lengths of the most stable AlnPn (n = 2~9) clusters (unit: Å)
表1. AlnPn (n = 2~9)团簇中最稳定异构体的平均键长(单位:Å)

Figure 1. Lowest energy isomers of AlnPn (n = 2~9) clusters
图1. AlnPn (n = 2~9)团簇低能异构体
其能量相较于Al2P2-a结构高出1.28 eV。从n = 3开始,AlnPn团簇中开始出现由Al-P键交替连接的笼状结构。Al3P3的三个低能异构体中,Al3P3-a是具有D3h点群的平面六元环,三个Al原子与三个P原子之间分别等距形成两个正三角形,是Al3和P3最稳定构型的结合。Al-P键长为2.23 Å。Al3P3-b与Al3P3-c是点群均为Cs的笼状结构。具有Td点群的Al4P4-a中,所有的Al-P键都为2.38 Å,每三个P或Al原子都可形成正三角形。Al4P4-a可看作是由两个Al2P2四元环结合而成,且因P原子孤对电子的存在使得Al原子比P原子更接近团簇的中心。此外,Al4P4-a开始出现船头结构(图2),6个Al-P键长相等,该结构与Al-P晶体中的成键方式类似。Al4P4-b与Al4P4-c的能量几乎是简并的,Al4P4-c具有Cs点群,可看做是2个Al原子分别担载在Al2P4八面体的2个面上。AlnPn (n = 2~4)中,最稳定异构体的Al-P键长均相等,表现出高对称性。随着原子数的增多,团簇由平面结构逐渐向立体结构过渡。次稳定异构体表现为多配位层,存在多种不同键长的Al-P键,多存在镜面对称。

Figure 2. Bow structure
图2. 船头结构
Al5P5-a是由2个五元环构成的扭曲五棱柱结构,出现了1个Al-Al键和1个P-P键。Al3P3船头结构发生变形,导致Al-P键长均不相等。Al5P5-b为Cs对称结构,AlP5共面,剩余的4个Al原子对称分布于AlP5面的两侧。具有D6d点群的Al6P6-a可看做是由2个方向相反的Al3P3-a结合形成双层环状结构,存在2种Al-P键,其中Al3P3六元环上的Al-P键长为2.33 Å,大于Al3P3-a中的Al-P键长(2.23 Å);连接两个Al3P3环的Al-P键长稍长,为2.38 Å。具有C2点群的Al6P6-b是笼状结构,由1个Al3P2五元环、1个Al2P3五元环和2个Al2P2单元组成,形成了2个Al3P3船头结构。
Al7P7-a笼状结构由1个Al3P3六元环、2个Al3P2五元环和2个Al2P3五元环组成,含2个Al3P3船头结构。具有S4点群的Al8P8-a团簇中,4个Al3P3四元环等价,与Al3P3-a相比稍有畸形,Al-P键长为2.32/2.38 Å,2个Al3P3船头结构等价,有2种不等价的Al原子和2种不等价的P原子。具有D4d点群的Al8P8-b是由2个Al4P4八元环形成的双层环状结构,每个P(Al)原子都与3个Al(P)成键,同Al4P4-a一样,P原子孤对电子的存在使得Al原子比P原子更加接近团簇中心。同层内Al-P键长为2.32 Å,层间Al-P键长稍长(2.38 Å)。Al9P9-a是C3h对称结构,其结构可看作两个Al3P3-a六元环相对,3个Al-P键将2个六元环连接起来,形成3个Al3P3船头结构,各键长对应相等。Al8P8-c与Al9P9-c结构中各原子空间分布则相对离散,可以认为是由两个结构组合而成。
根据AlnPn (n = 2~9)团簇的结构分析,发现随着原子数的增加,团簇逐步向笼状结构演变。在原子数相同的情况下,结构的对称性越高则其稳定性越高。在原子数较低时(n = 2, 3),二维平面结构相较于三维立体结构具有更高的稳定性。AlP团簇具有类似于AlP晶体中Al原子和P原子交替排列的特征。然而,Al5P5和Al7P7中存在Al-Al键和P-P键,Al-P键长小于Al-Al键长而大于P-P键长。我们计算了这三种键的键强,发现Al-P键强(3.03 eV)大于Al-Al键强(0.60 eV)而小于P-P键强(8.10 eV)。因此,Al原子和P原子间的相互作用强于Al-Al之间的相互作用而弱于P-P之间的相互作用。在Al6P6和Al9P9笼状结构中,构建基元Al3P3中的Al-P键长分别为2.33 Å和2.30/2.36 Å,大于Al3P3-a中的Al-P键长(2.23 Å),表明Al原子和P原子间的相互作用随着团簇尺寸的增大而减弱。
3.2. 稳定性
团簇的稳定性可由结合能来衡量,定义式为:
Eb = E(AlnPn) − nE(Al) − nE(P) (1)
表2给出了用B3LYP/6-31 + (d)和MP2/6-31 + g(d)方法计算的结合能Eb,发现AlnPn (n = 4~6, 8, 9)团簇在这两种方法下的稳定性顺序一致。图3为B3LYP/6-31 + G(d)方法下AlnPn (n = 2~9)中最稳定异构体的平均结合能Eb,从图中可以看到,平均结合能随着n的增大而增大,表明团簇的稳定性逐渐增强。能隙Eg是衡量体系化学稳定性的重要指标,其定义为最高占据分子轨道(HOMO)与最低未占据分子轨道(LUMO)的能量之差,AlnPn (n = 2~9)团簇的能隙Eg如表2所示,可见AlnPn (n = 2~9)团簇表现为半导体性质。图4为在B3LYP/6-31 + G(d)方法下AlnPn (n = 2~9)团簇中最稳定结构的能隙,可以看出当n = 2~4时,能隙逐渐减小,即团簇的稳定性逐渐降低;当n = 5时,能隙达到局域极大值,说明-Al5P5的稳定性大于相邻团簇;当n = 6~9时,能隙单调递增,表明团簇的稳定性逐渐增大。
Table 2. Binding energy Eb and energy gap Eg of AlnPn (n = 2~9) clusters (unit: eV)
表2. AlnPn (n = 2~9)团簇的结合能Eb和能隙Eg (单位:eV)
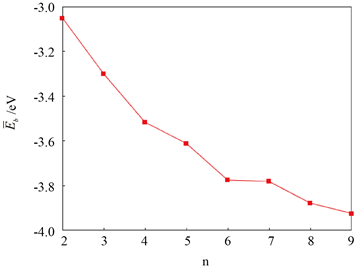
Figure 3. Average binding energies of the most stable structures in AlnPn (n = 2~9) clusters
图3. AlnPn (n = 2~9)团簇中最稳定结构的平均结合能

Figure 4. HOMO-LUMO gaps of the most stable structure in AlnPn (n = 2~9) clusters
图4. AlnPn (n = 2~9)团簇中最稳定结构的能隙
3.3. 电子结构
3.3.1. 电荷分布
Bader [28] 提出了分子中原子的电荷(Atoms In Molecule, AIM)模型,通过电子密度梯度为零的表面定义了每个原子在分子体系中的区域,提供了具有清晰物理意义的电子密度分布。本文基于B3LYP/6-31 + G(d)的优化结果,计算得到AlnPn (n = 2~9)团簇中最稳定异构体的AIM电荷,如表3所示。
Table 3. AIM charge of the most stable isomer in AlnPn (n = 2~9) clusters (unit: e)
表3. AlnPn (n = 2~9)团簇中最稳定异构体的AIM电荷电荷(单位:e)
对于AlnPn (n = 2, 3, 4),Al原子和P原子都等价,随着n的增大,Al→P的电荷转移由0.67e增大到1.83e。AlnPn (n = 5, 7)中都存在Al-Al键和P-P键。对于Al5P5,Al-Al键和P-P键中Al原子和P原子的电荷分别为1.02/1.28e和−1.05/−1.20e,Al-P键上的Al原子和P原子的电荷分别为1.77/1.80/1.80e和−1.77/−1.79/−1.83e。Al6P6中所有的Al原子和P原子都等价,所带电荷分别为1.89e和−1.89e。对于Al7P7,Al-Al键和P-P键中Al原子和P原子的电荷分别为1.47/1.48e和−1.13/−1.27e,Al-P键上的Al原子和P原子的电荷分别为1.83~1.88e和−1.84~−1.88e。在Al8P8团簇中,有2种不等价的Al原子和2种不等价的P原子,电荷分别为1.89/1.92e和−1.90/−1.91e。在Al9P9笼状结构中,2个Al3P3-a六元环等价,其中的Al原子和P原子所带电荷分别为1.92e和−1.92e;3个船头结构等价,其中Al原子和P原子的电荷分别为1.89e和−1.91e。
AlnPn (n = 5, 7)中都存在Al-Al键和P-P键,而这两种键中的Al原子和P原子所带电荷都比Al-P键上Al原子和P原子的电荷小,表明Al-P原子之间的电荷转移比Al-Al和P-P间更强,具有离子性质。对于AlnPn (n = 3, 6, 9),随着团簇尺寸的增大,构建基元Al3P3中,电正性的Al向电负性的P转移的电荷增加了,而这影响着每个团簇的成键性质。
3.3.2. 成键特性
为了了解AlP团簇的成键特性,我们研究了AlnPn (n = 2, 3, 6, 8)团簇的电子局域函数(Electron Localization Function, ELF)。电子局域函数是由Becke和Edgecombe [29] 提出,并由Savin等 [30] 共同完善的理论,常用来分析体系中的成键情况,反映原子之间所成化学键的相对强度。AlnPn (n = 2, 3, 6, 8)的ELF等值线如图5所示,在ELF等值线图中,吸引子可以将高度定域的电子区域可视化,例如原子中的内壳层、共价键以及孤对电子。小值表示低的电子密度,0.5和1.0分别表示完全离域和完全定域的电子对。

Figure 5. ELF contour of AlnPn (n = 2, 3, 6, 8)
图5. AlnPn (n = 2, 3, 6, 8)的ELF等值线
在Al2P2中,观察到Al原子外侧的吸引子为0.95,表明存在孤对电子.P原子的电负性较大,故周围的电子密度较大。P-P原子之间的吸引子为0.80,而Al-P之间没有明显的吸引子。随着n的增大,AlnPn (n = 3, 6)中P原子周围出现了孤对电子,而Al原子周围无孤对电子。Al-P之间均存在较大吸引子(0.85),说明Al和P之间的交替成键呈现了它们的主要成键特征。对于Al8P8-b,P原子外侧的吸引子增大为0.90,Al-P之间的吸引子仍为0.85,同样说明它们之间有较强的共价相互作用。AlnPn (n = 2, 3, 6, 8)团簇的总态密度(TDOS)和分态密度如图6所示,高斯展宽为0. 05 eV。可以清楚地看到,在能级较低处(−13.81~−19.71 eV)主要是由P 3s构成,在能级较高处(−5.00~−12.75 eV)主要是由Al 3s3p和P 3s3p构成,表明Al和P形成共价相互作用。
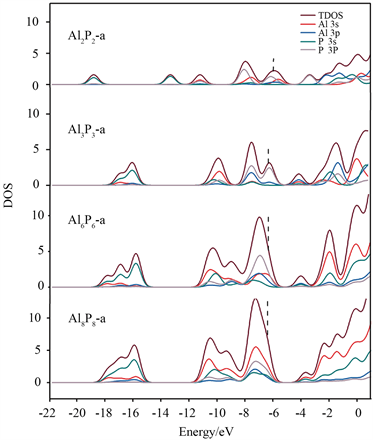
Figure 6. Density of states of AlnPn (n = 2, 3, 6, 8)
图6. AlnPn (n = 2, 3, 6, 8)的态密度
4. 结论
我们系统地研究了AlnPn (n = 2~9)团簇的几何结构、稳定性和电子性质。结果表明,随着原子数的增加,AlP团簇逐渐向笼状结构演变。AlP团簇具有类似于AlP晶体中Al原子和P原子交替排列的特征。键长分析表明,Al原子和P原子间的相互作用随着团簇尺寸的增大而减弱。AlP团簇的平均结合能随着团簇尺寸的增大而增大,表明团簇的稳定性逐渐增强。Al-P原子之间的电荷转移比Al-Al和P-P间更强,表现出离子性质。由电子局域函数和态密度分析发现,Al-P之间有较强的共价相互作用。
基金项目
国家级大学生创新创业训练项目(项目编号:202010616016)。
文章引用
彭从一,马 磊,马丽,和一鸣,王文杰. AlnPn (n = 2~9)团簇结构与性质的理论研究
Theoretical Study on the Structure and Properties of AlnPn (n = 2~9) Clusters[J]. 现代物理, 2021, 11(03): 41-51. https://doi.org/10.12677/MP.2021.113006
参考文献
- 1. 王广厚. 团簇的结构和奇异性质[J]. 物理学进展, 1993(Z1): 266-279.
- 2. 高雪情. 功能化铜纳米团簇复合材料的合成与应用[D]: [硕士学位论文]. 烟台: 烟台大学, 2020.
- 3. 周涛. 幻数团簇Al6CM4(M = Li, Na, K)及其组装晶体的理论研究[D]: [硕士学位论文]. 兰州: 西北师范大学, 2020.
- 4. 张颂, 黄意. 团簇物理学研究进展[J]. 科学技术创新, 2020(21): 20-21.
- 5. 王广厚. 团簇物理的新进展(I) [J]. 物理学进展, 1994(2): 121-172.
- 6. Burton, G.R., Xu, C., Arnold, C.C., et al. (1996) Photoelectron Spectroscopy and Zero Electron Kinetic Energy Spectroscopy of Germanium Cluster Anions. Journal of Chemical Physics, 104, 2757-2764. https://doi.org/10.1063/1.471098
- 7. 贾金锋, 窦瑞芬, 李绍春, 等. 纳米团簇晶体的制备和结构研究[J]. 世界科技研究与发展, 2004(5): 40-50.
- 8. 郭玲, 武海顺, 金志浩. 第一原理对AlnPm− (n + m = 5)团簇结构和稳定性研究[J]. 原子与分子物理学报, 2004(2): 169-176.
- 9. Gómezh, T.T.R. and Neumark, D.M. (2001) Anion Pho-toelectron Spectroscopy of Aluminum Phosphide Clusters. Journal of Physical Chemistry A, 105, 6886-6893. https://doi.org/10.1021/jp0105544
- 10. Huang, R.B. (1993) Mass Spectroscopic Studies of AlnXm (X = O, S, P, As, C). Chinese Journal of Structural Chemistry, 6, 466-470.
- 11. Liu, Z., Wang, C., Huang, R., et al. (1995) Mass Distributions of Binary Aluminum Cluster Anions AlnXm− (X = O, S, P, AS, C). International Journal of Mass Spec-trometry & Ion Processes, 141, 201-208. https://doi.org/10.1016/0168-1176(95)04103-R
- 12. Al-Laham, M.A., Trucks, G.W. and Raghavachari, K. (1992) Theoretical Study of Small Aluminum Phosphide and Magnesium Sulfide Clusters. Journal of Chemical Physics, 96, 1137-1149. https://doi.org/10.1063/1.462201
- 13. Tomasulo, A. and Ramakrishna, M.V. (1996) Density Func-tional Studies of Aluminum Phosphide Cluster Structures. Journal of Chemical Physics, 105, 10449-10455. https://doi.org/10.1063/1.472928
- 14. Feng, P.Y. and Balasubramanlan, K. (1999) Spectroscopic Properties of Al2P2, Al2P2+, and Al2P2− and Comparison with Their Ga and in Analogues. Journal of Physical Chemistry A, 103, 9093-9099. https://doi.org/10.1021/jp991542+
- 15. Ping, Y., et al. (2000) Potential Energy Surfaces of Electronic States of AlP2, Al2P and Their Ions. Chemical Physics Letters, 318, 417-426.
- 16. Archibong, E., Gregorius, R.M. and Alexander, S.A. (2000) Structures and Electron Detachment Energies of AlP2− and Al2P2−. Chemical Physics Letters, 321, 253-261. https://doi.org/10.1016/S0009-2614(00)00355-9
- 17. Archibong, E.F., Stamant, A., Goh, S.K., et al. (2002) Structure and Electron Detachment Energies of Al3P− and Al3P3. The Journal of Physical Chemistry A, 106, 5932-5937. https://doi.org/10.1021/jp014669j
- 18. Costales, A., Kandalam, A.K., Franco, R., et al. (2002) Theoretical Study of Structural and Vibrational Properties of (AlP)n, (AlAs)n, (GaP)n, (GaAs)n, (InP)n, and (InAs)n Clusters with n = 1, 2, 3. Journal of Physical Chemistry B, 106, 1940-1944. https://doi.org/10.1021/jp013906f
- 19. Qu, Y. and Bian, X. (2005) Electronic Structure and Stability of AlnPn (n = 2 - 4) Clusters. Journal of Computational Chemistry, 26, 226-234. https://doi.org/10.1002/jcc.20146
- 20. Zhao, J., Wang, L., Jia, J., et al. (2007) Lowest-Energy Structures of AlnPn (n = 1 - 9) Clusters from Density Functional Theory. Chemical Physics Letters, 443, 29-33. https://doi.org/10.1016/j.cplett.2007.06.055
- 21. Karamanis, P. and Leszczynski, J. (2008) Correlations between Bonding, Size, and Second Hyperpolarizability (Gamma) of Small Semiconductor Clusters: Ab initio Study on AlnPn Clusters with n = 2, 3, 4, 6, and 9. Journal of Chemical Physics, 128, Article ID: 154323. https://doi.org/10.1063/1.2902287
- 22. Lu, T. and Chen, F. (2012) Multiwfn: A Multifunc-tional Wavefunction Analyzer. Journal of Computational Chemistry, 33, 580-592. https://doi.org/10.1002/jcc.22885
- 23. Frisch, M.T.G., Schlegel, H., Scuseria, G., Robb, M., Cheeseman, J., et al. (2009) Gaussian 09. Gaussian Inc., Wallingford, Revision D.01.
- 24. Miehlich, B., Savin, A., Stoll, H., et al. (1989) Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chemical Physics Letters, 157, 200-206. https://doi.org/10.1016/0009-2614(89)87234-3
- 25. Frisch, M.J., Head-Gordon, M. and Pople, J.A. (1990) Semi-Direct Algorithms for the MP2 Energy and Gradient. Chemical Physics Letters, 166, 281-289. https://doi.org/10.1016/0009-2614(90)80030-H
- 26. Head-Gordon, M. and Head-Gordon, T. (1994) Analytic MP2 Frequencies without Fifth-Order Storage. Theory and Application to Bifurcated Hydrogen Bonds in the Water Hexamer. Chemical Physics Letters, 220, 122. https://doi.org/10.1016/0009-2614(94)00116-2
- 27. Lu, T. and Chen, F.W. (2011) Multiwfn: A Multifunctional Wavefunction Analyzer. Journal of Computational Chemistry, 33, 580-592. https://doi.org/10.1002/jcc.22885
- 28. Bader, R.F.W. (1992) A Quantum Theory of Molecular Structure and Its Applications. Cheminform, 23, 893-928. https://doi.org/10.1002/chin.199203324
- 29. Becke, A.D. and Edgecombe, K.E. (1990) A Simple Measure of Electron Localization in Atomic and Molecular Systems. Journal of Chemical Physics, 92, 5397-5403. https://doi.org/10.1063/1.458517
- 30. Savin, A., Nesper, R., Wengert, S., et al. (2003) ELF: The Electron Loca-lization Function. Angewandte Chemie International Edition, 36, 1808-1832. https://doi.org/10.1002/anie.199718081
NOTES
*通讯作者。
