设为首页 加入收藏

1. 引言

西方数学之发展，主要以人为之抽象为主，往往脱离或忽视了“数”相应物之存在与演化，因此会遭遇所谓之三次数学危机。中国古人之数学抽象，更接近意象思维^[1]。这就使得东西方之数学重点迥异。为说明此点，在此以西方数学之三大危机为例。

西方数学之第一次危机发生在公元前5世纪，主要是发现了无理数却因无法理解而拒绝之。古希腊以Pythagoras(约前580~前500年)为首之Pythagoras学派认为：任何两条线段之长度比，都可以用两个整数之比来表示，并称之为可公度。两个整数相比实际上包括了整数和分数(统称为有理数)。因此，Pythagoras认为世界上只存在着整数与分数，除此以外，别无他数。可是不久就出现一个问题。Pythagoras有一个叫Hippias的学生发现，若正方形之边长为1，则由勾股定理，对角线之长为。然而到底等于多少呢？是整数？还是分数呢？因为一定比1大，比2小，因此其不是整数。而更要命的是，整个Pythagoras学派都找不出对应之分数。由于Pythagoras认为世界上只有整数与分数，因此到底是什么数引起了Pythagoras学派极大之苦恼与恐慌。Hippias之发现推翻了Pythagoras之结论，动摇了该学派之核心基础。Hippias因害怕被迫害而秘密潜逃，但不久后仍被其同门抓获，并以泄密罪被淹死在地中海里。而这种新数，由于不好理解，后来被命名为“无理数”。

有理数与无理数之主要区别有两点：第一，有理数能写成有限小数或无限循环小数，而无理数只能写成无限不循环小数(据此，无理数被定义为无限不循环小数)；第二，所有有理数都可以写成两个整数之比(即可公度)，而无理数不能写成两个整数之比，即不可公度。

记得以前读初中时，有理数被定义为整数、有限小数和无限循环小数之总和，或干脆称之为分数；而无理数被定义为无限不循环小数或不能写成分数之数。但这样做其实是令人疑惑的，因为人们无法判断一个数是无限不循环的还是经历了很长一段不循环后再循环。因此“无限不循环”之说法既不合理也不严格。这一困难使数学史上数域之扩张停滞了两千多年。

公元前6世纪Pythagoras学派发现了无理数，但直到2400年后才产生包括无理数在内的实数之严格定义；学生在初中阶段开始接触无理数，但直到大学毕业仍然不明白无理数之实质含义。除了根式、圆周率、黄金分割比与自然对数底数等常见之无理数外，学生们甚至找不出别的无理数。

虽然无理数是如此长久而持续地困扰着数学家，但在应用方面，绝大多数人却得心应手。如对于圆周率π，循环还是不循环是不重要的。美国天文学家西蒙·纽克姆曾说：“十位小数就足以使地球周界准确到一英寸以内，三十位小数便能使整个可见宇宙的四周准确到连最强大的显微镜都不能分辨的一个量^[2]。”可见，关心无理数之更多小数位是没有必要的(实际上也是无法完成的)，因此也就没必要在此浪费更多抽象思维，仅仅在意象思维中“只可意会，不可言传”就好了。

Hippias之发现无理数，显然得益于Pythagoras定理，中国人称之为勾股定理，早在Pythagoras之前就存在了。因此，中国古人极有可能更早地发现了无理数，只不过他们并未大惊小怪，也未郑重其事地记载。他们或许认为，这些数只要能意会，在使用时用有理数去逼近就可以了。因此，在中国并未出现此一数学危机。至于中国古人因何如此淡定，请读者继续往下看。

西方数学之第二次危机是由无穷小量引起的，它反映了有限与无穷之矛盾。很早以前，人们就对长度、面积、体积等度量问题深感兴趣。古希腊天文学家、数学家Eudoxus(前408~前355年)引入量之观念来考虑连续变化，并完全依据几何来严格处理连续量，从而造成数与量之长期脱离。不久，便产生了以Zeno(约前490~前425年)悖论为代表之数学危机。

Zeno悖论有四个，由于大同小异，在此只详细介绍前两个：

1) 运动不存在。因为运动物体到达目的地之前必须先到达中点，而到达中点之前又必须到达中点之中点∙∙∙∙∙∙如此下去，到达目的地必须先通过无限多个点，而这在有限之时间内是无法办到的。

2) 跑步健将Achilles追不上在其前面之乌龟。因为乌龟在前，Achilles必须先到达乌龟之起点，然后用第一个悖论的逻辑，乌龟永远在其前头。

这说明古希腊人当时已经在面对无穷小引起之混乱。

第三次数学危机近在19世纪末至20世纪初，当时之数学空前地兴旺发达，大多数数学家都在推动公理化运动，探讨数学之基础与数理逻辑等问题。当时也是现代数学一些新分支之兴起时期，如：抽象代数学、点集拓扑学、代数拓扑学、泛函分析、测度论与积分理论等学科。这些学科之出现，使得公理体系之构建变得极其重要。

是否存在一种公理体系，普适所有数学学科？答案是否定的。三角形之内角和是否等于180度？过直线外一点是否有且只有一条直线与已知直线平行？若读者只学过中学阶段之平面几何，则答案是肯定的。但实际上，事实并非如此。过直线外一点，平行线可以是唯一的，也可以是无限多的，甚至还可以一条也没有。而三角形内角和等于180度，也仅仅是在Euclid(活跃于前300年左右)几何体系中才成立。若三角形内角和大于180度，则属于Riemann(1826~1866)几何，此时两点可以决定无穷条直线；若三角形内角和小于180度，则属于Lobachevsky(1792~1856)几何，此时直线外可能不存在平行线。

上述例子说明，不存在囊括一切元素之集合。英国哲学家、数学家W. Russell(1872~1970)于1900年前后提出如下著名悖论：

将所有集合分为两类，第一类中之集合以其自身为元素，第二类中之集合不以自身为元素。假设第一类集合所组成之集合为P，第二类集合所组成之集合为Q，即

则抑或？

若，则根据第一类集合之定义，必有。但是Q中任何集合都有的性质，所以又有，如此引出矛盾。若，根据第一类集合之定义，必有，则，所以，仍旧矛盾。

Russell悖论之通俗版本是：某个理发师只给那些不自己理发之人理发。试问：该理发师自己之头发谁来理呢？显然，不管如何回答，都会陷入二难境地。《唐·吉诃德》中有一则故事：桑丘跑到一个小岛做国王后，命令每个进入该岛之人都必须回答“你来此何干？”这一问题。若答对了，就允许其在岛上游玩，否则将其绞死。后来有人回答：“我来此就为被绞死。”试问桑丘是该让他在岛上玩，还是将其绞死？这显然也是个Russell悖论。

上述集合论悖论，在现实生活中亦处处可见。如人类社会普遍实行之行政领导制度，从根本上说即含有这种集合论悖论机制。从“官”之体制和职能来讲，其代表着所管范围内全体公民之整体利益；但从人员对象来讲，“官”又是集合中之一员。即使从集合外派人去领导，本质上仍改变不了其为所辖集合中一员之实质，从而产生了“元素大于集合”之悖论。这就是任何一个社会，任何一种制度下，官场中总有徇私舞弊、贪赃枉法等腐败现象且屡打不绝之症结所在。

还可以宗教为例。教会中人经常说“上帝与你同在”、“上帝创造了这个宇宙”等，这表明上帝和我们同在一个宇宙。然而由于“上帝是万能的”，这就产生了元素大于集合之悖论。况且，在上帝创造这个宇宙之前，他老人家住在哪里？《圣经》好像没说过有两个宇宙。(前些年听说罗马教廷终于在350多年后给Galileo平反，承认其天文学说，这是否意味着教会终于承认上帝既未创造宇宙也非万能的呢？)

平时只要多做留意我们还可发现，类似之悖论在经济社会中、心理学上乃至日常生活里都有其表现。若能把这种思想上升到意识，将更有利于社会治理、通用管理和科研等活动。

2. 精度与测度

《庄子·天下》曰：“一尺之棰，日取其半，万世不竭。”庄子并非职业数学家或科学家，但关于无限、无穷小之现象，他似乎已了然于胸。中国古代不会出现这一数学危机，窃以为得益于中国古人之生活态度。要说明这一点，还需引入现代数学之分支之一，即分形几何。从哲学上来讲，分形几何研究的就是观测精度与物体真实测度之关系。测度为数学专业词汇，非数学专业之读者可简单将其理解为长度、面积与体积之总称。

如两个山头间之距离，若用光波来测量，直接照射过去，可得S₁；若是用皮尺来测量，则必须下山、上山，可得S₂；下山与上山之路上难免有些土包、坑洼、裂缝，虽然人可一跃而过，但若测量之主体生物只是蚂蚁，它只好爬上小土包、爬下坑洼、爬进裂缝，然后继续前进，才能得到新长度S₃。不难想象，此三次测量满足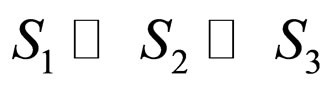，其中符号“”表示“远远小于”。之所以会如此，是因为提高了测量之精度。若还能找到单位长度比蚂蚁之度量单位还小之生物或尺子，则可测出更大之长度。由此可以推论，若观测精度无限大，即尺子之单位长度或最小刻度无穷小，则可测得任意不同两点之间之真实距离为无穷大。这当然也是个哲学悖论，因为我们总能以有限速度在有限时间内到达另一个可落脚处，这又是如何做到的呢？窃以为，凡此种种，皆取决于观测之精度。

中庸之道告诉我等，做人不可精度要求得太高，“人至察则无徒，水至清则无鱼”。也许，佛祖——若真有佛祖——对世界正是采用了极低之观测精度，才能形成“众生平等”之观测结果，才能认识到“众生皆有佛性”。若采用较低之观测精度，此时观测工具(可以是实在的尺子，也可以是虚拟之物)之单位长度较大，则高精度之褶皱、起伏都将被忽略。读者不妨想象一下，你在走路时可以轻易地忽略路面上对蚂蚁造成很大障碍之小裂缝，这其实就是你采用较大之单位长度(对应低精度)从而抹杀高精度小裂缝之生动实例。

明白精度与测度之关系后，再回头来看Zeno悖论，就会豁朗开朗，并明白其症结所在。Zeno悖论，不过是无穷次被放大之精度所带来之认知性矛盾而已。由于任何物种与机器之观测精度总是有限的，因此Zeno悖论也仅仅是存在于想象中而已，现实中并不会发生。但西方人为此迷惘了数百年，实在令人费解。

《庄子·天下》曰：“至大无外，谓之大一；至小无内，谓之小一。”即不存在最大之集合或最小之集合。《管子·内业篇》也道：“灵气在心，一来一逝。其细无内，其大无外。”(明)罗懋登《三宝太监西洋记·第一回》“盂兰盆佛爷揭谛 补陀山菩萨会神”中解释佛祖曰：“能变能化，无大无不大，无通无不通。”这些其实都很好地解释了Russell悖论是不会发生的。中国古人构造神话体系时尚且让神仙各司其职，怎么可能会认为存在包含一切元素或集合之集合呢？(美国)天文学家Carl Sagan(卡尔·萨根，1934~1996)曾说：“若你钻进一电子深处，会发现其本身乃一个宇宙，这使你回想起20世纪50年代的那些科幻故事。里面，大量小得多的别的粒子组成了相当于当地星系和较小之结构，它们本身就是下一层次之宇宙。如此永远下去，一个逐步推进的过程，宇宙中的宇宙，永无尽头，往上也一样^[3]。”这其实与《庄子·天下》之思想暗合。

不管是古代中国还是现代中国，都不会有人提出Russell悖论，也不会产生第三次数学危机。这是因为，中国人很热衷于“常识”，而很少去追究常识背后之原理。在中国，不管多普通之学生，也不可能像牛津大学之博士生那样，在毕业论文中只讨论“加糖是为了使冰激凌变甜”或“加粗、加黑是为了使文字更显眼”之类的课题(本卷1.5节还有相关叙述)。对于常识之追究，使得西方终于走上了科学之路，也饱尝了种种思想危机；而中国人对常识只采取默认之态度，虽然不可能很早就进入科学，但也低精度地“忽略”了种种思想危机。

中国古人低精度之生活与治学态度，使得在古代一直不能发展出系统之科学，更不可能向(需要高精度之)微观世界迈进。再如，中国人早在两千多年前就知道宇宙是空间和时间之总和(见本书卷二之2.1.2节)，在时空观上达到了超前西方人两千三百余年之辉煌见解，但他们并未进一步去探讨空间之维度问题。因为古中国之学者们几乎不考虑纯粹抽象之数学，这种低精度—因为现实问题精度都不会太高—之治学态度也就决定了研究问题之取向。而西方之数学家们喜欢放纵思维于纯粹抽象，关于这一点，从当今之高等数学中充满了高维度变量就可见一斑。

关于精度决定测度之问题，要继续论证，则还需引入维度之概念。若某空间中之元素“至少”需要n个变量来标记，则该空间为n维空间。比如说，数轴只需要一个变量标记，因此其为一维；平面至少需要两个变量，则其为二维；立方体至少需要三个变量，则其为三维。这就是一维直线、二维平面、三维空间之来历。该定义是基于坐标系的，或者说是找线性空间之基(最小无关向量组)。关于空间之维度，还有拓扑定义，本文暂不涉及。

如图1所示，设电线两端分别为A、B，规定其一为参照点，设为A。其上之小鸟，不管它们朝向如何，都只需要一个变量就可将其位置标记出来。这个变量，就是鸟所站立之处距离A点之长度，设为x。根据上述代数定义，以小鸟为参照来观测，则电线只是一维的。

但若在电线上之生物并非小鸟，而是只小蚂蚁，则情况将大大不同。由于蚂蚁很小，若只知道它距A点之长度，则很可能仍找不到它。因为电线之截面直径比蚂蚁身躯要大，蚂蚁可能会被遮挡在另一面。因此，要想精准地找到蚂蚁，则至少需要两个变量，其一为上述之x，另一乃绕电线表面之观测角度，设为y。如此看来，以蚂蚁为参照来观测，则电线是二维的。读者可以试着想象站在太空看北半球，则南半球之人会被地球挡住，因此地球表面定位，需要二维变量，通常采用经度和纬度。

再来考虑可穿透金属之细菌。由于它可以渗入电线内部，因此即便知道了长度x、角度y，也不一定能找到细菌在哪。要想精准定位细菌，这时还需要知道其钻入之深度，设为z。由此看来，以细菌为参照来观测，电线竟然变成了三维的。读者试想，从泥土里挖蚯蚓，是不是要知道深度呢？

3. 一些评述

事实上，若不断地增加观测之精度，则电线之维度会不断增加。在目前之(理论)精度范围内，它可扩充至九维。这一点，是古中国之学者难以理解也无法接受的。

图1. 电线的观测维度

就在西方学者在现实世界探索精度型之科学时，古中国之学者却更致力于虚实结合而偏向于虚拟世界。古中国人传承《易经》中“孤阳不长，独阴不生”之哲学观点，因此认为对偶之阴阳二象具有互补性。阴阳二象本身是各自独立的，且互相不可替代。当我们同时从阴阳或虚实之对立统一的两面去考察某系统之结构特征时，则称该系统可称为一个完备(度量)空间。

完备(度量)空间乃现代数学中之概念，该空间中之任何Cauchy序列都收敛在该空间之内。有理数域是不完备的，如之收敛序列

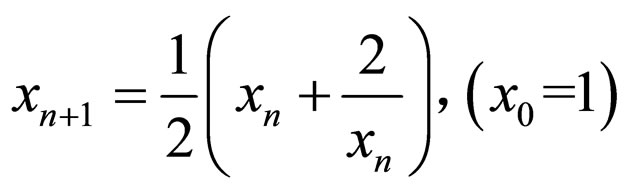
是Cauchy序列，但其极限不属于有理数。开区间(0, 1)也不是完备的，如调和序列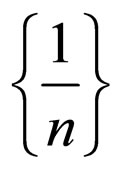是Cauchy序列，其极限为0，而。实数域是完备的。直观来看，一个空间完备就是指空间内部没有“缝隙”且边界上无缺陷。专业点来看，一个空间完备同一个集合之闭包是类似的，且完备空间之闭子集也是完备的。

也许正是实数之完备性导致了古中国之学者们裹足不前，没有进一步考虑虚数。然而二象结构是一个自然意义下最优之互补匹配，正如弓、箭必须合在一起才能杀敌制胜，软、硬件合二为一才能运行电脑一样。因此，虚数，乃至复数之产生，是迟早而必然的。若没有虚数，实数之互补、实数之阴象，又会是什么呢？

虚数之产生，使得实数与虚数阴阳合壁而成为复数。复数域更具有完备性，其功能比其对偶二象分别功能之和更强。即，复数x + iy除了具有实数空间之所有性质外，还具有一些额外性质。如指数函数e^z之周期性，三角函数sinz，cosz之无界性，对数函数Lnz之无穷多值性等。这都是证明1 + 1 > 2之绝佳范例。

一个完备空间具有同一性与稳定性，此正古人所谓之“近朱者赤，近墨者黑”。虽然庄子等很早就论述了极限思想，但对于极限型之精度却毫不关心，因此空间完备性之严谨理论也并未构造。古中国人似乎只关心抽象世界之完备，如自古就有“夫妻相”之说。根据《20世纪的23项突破》之统计报告：和睦生活在一起之女性，其经期将趋于同步。两个放在一起之单摆在频率竞争下，会形成可公度之运动轨道，叫锁相轨道。

完备空间自身内部还具有对称结构，如：复数域众阴(虚数域)、阳(实数域)二象达到虚实均衡，可谓之对称。几何是一种显对称，函数是一种隐对称，代数则是一种终极之结构对称^[4]。

参考文献 (References)

[1]       刘长林. 中国象科学观: 易、道与兵、医[M]. 北京: 社会科学文献出版社, 2008.

[2]       丹齐克. 苏仲湘, 译. 数: 科学的语言[M]. 上海: 上海教育出版社, 2000: 98.

[3]       卡尔·萨根. 周秋麟, 吴衣俤等, 译. 卡尔·萨根的宇宙[M]. 长春: 吉林人民出版社, 1998.

[4]       熊辉. 代数与中国古代经典[M]. 北京: 现代教育出版社, 2010.

NOTES

^*通讯作者。熊辉，1978-，男，博士，副教授，主要从事于偏微分方程、数学哲学与心理测量的研究。