Modeling and Simulation
Vol.05 No.04(2016), Article ID:18919,5
pages
10.12677/MOS.2016.54016
Applications of Weierstrass Theorem in Regression Analysis and Mathematical Modeling
Xiao Yu*, Zhan Li
School of Communication and Information Engineering, University of Electronic Science and Technology of China, Chengdu Sichuan
Received: Oct. 19th, 2016; accepted: Nov. 8th, 2016; published: Nov. 11th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Based on Weierstrass’ approximation theorem, the mathematical principle of a nonlinear regression model which can be approximated by a polynomial regression model is interpreted, and then the general method of converting the multivariate nonlinear regression analysis into the multivariate linear regression analysis is introduced. To show the practicability and validity, a practical application example is given.
Keywords:Weierstrass’ Approximation Theorem, Regression Analysis, Mathematical Model

Weierstrass逼近定理在回归分析建模中的应用
于霄*,李崭
电子科技大学通信与信息工程学院,四川 成都
收稿日期:2016年10月19日;录用日期:2016年11月8日;发布日期:2016年11月11日

摘 要
基于Weierstrass逼近定理,阐释了将一般非线性回归模型近似为多项式模型来处理的数学原理,从而引入了把多元非线性回归分析转化为多元线性回归分析的一般方法,并且通过实际应用案例分析表明该方法的实用性和有效性。
关键词 :Weierstrass逼近定理,回归分析,数学模型

1. 引言
众所周知,在许多实际问题中都需要用量化的方法研究两个(或多个)变量之间存在的关系,即根据变量的观测值近似地建立表达变量间关系的曲线(或广义曲面)方程,也就是所谓的曲线(或曲面)拟合问题。
运用统计分析方法,近似地建立变量间的数学方程式,检验和比较一个或一组变量对所关注的变量的影响程度,进而用一个或一组变量的变化,解释、预测和控制所关注变量的变化,这就是所谓的回归分析。在回归分析中,所关注的变量称为因变量,记作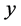 ;而影响因变量变化的另一个或一组变量称为
;而影响因变量变化的另一个或一组变量称为
自变量或影响变量,记作 或
或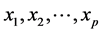 。根据自变量的个数,可以把回归分析划分为一元的或多元的。回归模型表达如下:
。根据自变量的个数,可以把回归分析划分为一元的或多元的。回归模型表达如下:
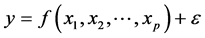
其中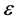 是均值为零的正态随机变量,表示随机误差。当
是均值为零的正态随机变量,表示随机误差。当 是
是 元线性函数时,则称为
元线性函数时,则称为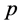 元线性回归模型;当
元线性回归模型;当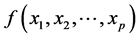 是
是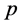 元非线性函数时,则称为
元非线性函数时,则称为 元非线性回归模型。回归分析的首要任务就是要根据样本值(或观测值)确定多元函数
元非线性回归模型。回归分析的首要任务就是要根据样本值(或观测值)确定多元函数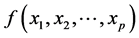 的具体数学表达式,从而得到回归方程:
的具体数学表达式,从而得到回归方程:
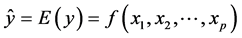 .
.
对于此类问题,数理统计学所提供的常用和成熟的数据分析工具是线性回归分析理论和方法。但是在实际问题中,因变量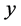 和影响变量
和影响变量 之间往往并不存在显著的线性相关关系,而多是非线性相关关系。通常的处理方法是借助其它信息或专业知识,预知非线性函数
之间往往并不存在显著的线性相关关系,而多是非线性相关关系。通常的处理方法是借助其它信息或专业知识,预知非线性函数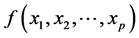 的函数类型,然后通过适当的变量替换,将非线性回归模型转化为线性回归模型来研究。当
的函数类型,然后通过适当的变量替换,将非线性回归模型转化为线性回归模型来研究。当 时,即对于一元回归模型而言,这一方法比较容易实现。首先通过观察确定相关点
时,即对于一元回归模型而言,这一方法比较容易实现。首先通过观察确定相关点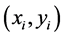 集中在一条什么样的曲线附近来预判一元非线性函数
集中在一条什么样的曲线附近来预判一元非线性函数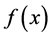 的函数类型,然后通过适当的变量替换转化为一元线性回归模型来处理。然而,当
的函数类型,然后通过适当的变量替换转化为一元线性回归模型来处理。然而,当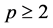 时,即对于多元非线性回归模型来说,这种方法很难实行,从而难以事先确定多元非线性函数
时,即对于多元非线性回归模型来说,这种方法很难实行,从而难以事先确定多元非线性函数 的函数类型。因此,如何选择合适的多元非线性回归模型是个值得研究的问题,而Weierstrass逼近定理提示我们,很多情况下可以近似为多项式模型。
的函数类型。因此,如何选择合适的多元非线性回归模型是个值得研究的问题,而Weierstrass逼近定理提示我们,很多情况下可以近似为多项式模型。
2. Weierstrass逼近定理
通常所指的Weierstrass逼近定理有两个,一个是多项式函数列逼近定理,另一个是三角函数列逼近定理。我们这里主要介绍Weierstrass第一逼近定理,其表述如下(相关细节可参见Rudin [1] ):
定理 [1] 。设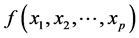 是定义在有界闭区域
是定义在有界闭区域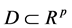 上的连续函数,则对任给的
上的连续函数,则对任给的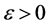 ,都存在
,都存在 元多项式
元多项式 ,使得对一切
,使得对一切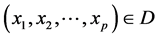 一致地成立
一致地成立
 .
.
3. 多元多项式回归模型
根据Weierstrass逼近定理知,任一多元连续函数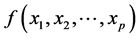 都可以近似为多项式函数
都可以近似为多项式函数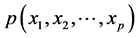 ,因而,一般的多元非线性回归模型就可以近似为如下多元多项式回归模型来研究:
,因而,一般的多元非线性回归模型就可以近似为如下多元多项式回归模型来研究:
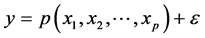
而上述多元多项式回归模型又可以通过适当的变量替换转化为多元线性回归模型来研究。
4. 应用案例分析
下面给出上述方法的一个实际应用案例分析,问题源于全国大学生数学建模竞赛的赛题(参见 [2] ),但是为了避免繁琐的细节冲淡主题,我们对原题进行了简化和改编。
4.1. 问题:农作物施肥效果分析
在土豆生长期间,施用不同量的氮肥(N)和钾肥(K),得到土豆产量交叉实验结果见下表。求土豆产量与施肥量之间的关系。
首先,为了计算方便,对数据作中心标准化处理,即令
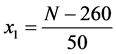 ,
,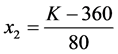
这里260和360是中位数,50和80是公差,如此中心标准化处理之后, 和
和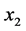 的三个不同取值被简化成−1,0,1。
的三个不同取值被简化成−1,0,1。
如果说,施肥量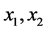 与土豆产量
与土豆产量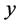 有密切的关系,则应有
有密切的关系,则应有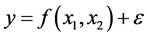 ,其中
,其中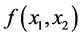 可能是线性函数,也可能是非线性函数。探求
可能是线性函数,也可能是非线性函数。探求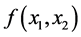 的表达式是本问题的目的,需运用回归分析方法。
的表达式是本问题的目的,需运用回归分析方法。
4.2. 失败的尝试:线性回归模型
模型1: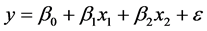
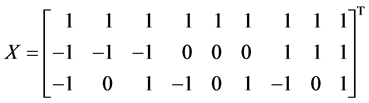 ,
,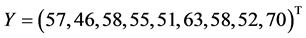 .
.
运用SPSS统计软件计算得回归系数的最小二乘估计为:
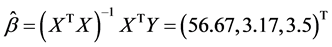 .
.
从而得线性回归方程为: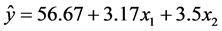 。经方差分析得:离差平方和
。经方差分析得:离差平方和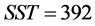 ,回归平方和
,回归平方和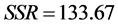 。从而,多重判定系数
。从而,多重判定系数
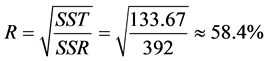 .
.
因为判定系数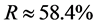 ,取值过于偏小,说明所得线性回归方程拟合实际情况的效果不好,即
,取值过于偏小,说明所得线性回归方程拟合实际情况的效果不好,即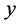 与
与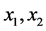 之间并不存在显著的线性相关关系。
之间并不存在显著的线性相关关系。
4.3. 有效的模型:多项式回归模型
既然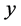 与
与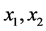 之间并不存在显著的线性相关关系,则
之间并不存在显著的线性相关关系,则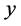 与
与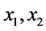 之间存在的只能是某种非线性相关关系,即
之间存在的只能是某种非线性相关关系,即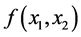 是非线性函数。据Weierstrass逼近定理知,
是非线性函数。据Weierstrass逼近定理知,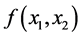 可以近似表示成某个二元多项式。我们依然从最简单的二元二次多项式开始,即尝试建立如下二次多项式回归模型:
可以近似表示成某个二元多项式。我们依然从最简单的二元二次多项式开始,即尝试建立如下二次多项式回归模型:
模型2: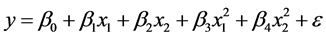
通过变量替换,令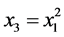 ,
,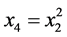 ,转化为四元线性模型来处理,此时有
,转化为四元线性模型来处理,此时有
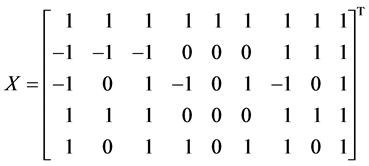
运用SPSS统计软件计算得回归系数的最小二乘估计为:
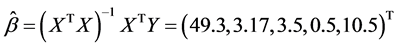 .
.
从而得二次多项式回归方程如下:
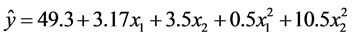
经方差分析得:回归平方和 。从而,多重判定系数
。从而,多重判定系数
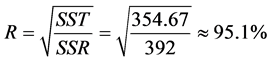 .
.
由于判定系数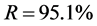 ,说明所得二次多项式回归方程拟合实际情况的效果很好。
,说明所得二次多项式回归方程拟合实际情况的效果很好。
4.4. 完善的模型:含交叉项的多项式回归模型
显然,模型2漏掉了反应氮肥和钾肥交互作用的交叉项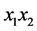 ,但常识告诉我们这种交互作用是不应该被忽略的。因此,进一步考虑如下含交叉项的多项式模型:
,但常识告诉我们这种交互作用是不应该被忽略的。因此,进一步考虑如下含交叉项的多项式模型:
模型3: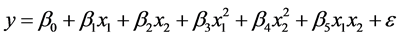
通过变量替换,令 ,转化为五元线性模型来处理,此时有
,转化为五元线性模型来处理,此时有

运用SPSS统计软件计算得回归系数的最小二乘估计为:
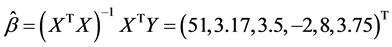 .
.
从而得含交叉项的二次多项式回归方程如下:
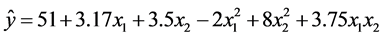
经方差分析得:回归平方和 ,残差平方和
,残差平方和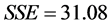 。从而,多重判定系数
。从而,多重判定系数
 .
.
因判定系数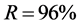 ,说明所得含交叉项的二次多项式回归方程拟合实际情况的效果进一步得到改善。进一步对显著性进行
,说明所得含交叉项的二次多项式回归方程拟合实际情况的效果进一步得到改善。进一步对显著性进行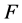 检验,取显著水平
检验,取显著水平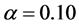 ,则
,则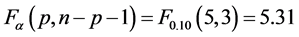 ,而
,而
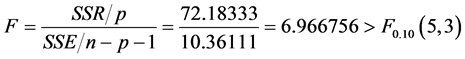
这说明所得到的含交叉项的二次多项式回归方程所表达的氮肥和钾肥的施肥量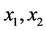 与土豆产量
与土豆产量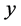 之间的多项式相关关系是显著的(
之间的多项式相关关系是显著的( )。
)。
5. 结束语
综上所述,我们不仅根据Weierstrass逼近定理,从数学理论上解释了通常情况下以多项式回归模型近似表达一般非线性回归模型的合理性;而且通过具体的实际案例分析展示了这一方法的可行性和优越性。这一方法,给实际的众多非线性问题的数学建模提供了一个有效的解决方案和理论依据,对实际应用具有一定的指导意义。
事实上,近年来众多文献(参见 [3] [4] [5] [6] )的实证研究证明,运用多元多项式回归分析方法探求一组影响变量和因变量之间的非线性相关关系的具体数学表达式的方法,在网络故障分析及预测、智能手机图像颜色校正研究、人体微量元素含量医学测定、农作物种子生活力评价研究等众多领域的应用中都是行之有效的。
文章引用
于霄,李崭. Weierstrass逼近定理在回归分析建模中的应用
Applications of Weierstrass Theorem in Regression Analysis and Mathematical Modeling[J]. 建模与仿真, 2016, 05(04): 118-122. http://dx.doi.org/10.12677/MOS.2016.54016
参考文献 (References)
- 1. Rudin, W. (1976) Principles of Mathematical Analysis. McGraw-Hill Companies, Inc., New York.
- 2. 白其峥. 数学建模案例分析[M]. 北京: 海洋出版社, 2000.
- 3. 邓力, 范庚, 刘治学. 基于回归分析方法的网络故障预测[J]. 计算机工程, 2012, 38(20): 251-255.
- 4. 邓如意, 胥义, 王健. 基于多项式回归模型的智能手机图像颜色校正研究[J]. 软件导刊, 2016, 15(1): 173-175.
- 5. 刘泽春, 李培军. 二次多项曲线拟合在锌测定中的应用[J]. 浙江预防医学, 2015, 27(12): 1294-1296.
- 6. 李晓明, 刘明, 宋冰燕, 田向荣. 基于三次多项式回归法的大豆种子生活力评价[J]. 吉林大学学报(自然科学版), 2012, 33(5): 83-91.