Advances in Applied Mathematics
Vol.05 No.02(2016), Article ID:17494,6
pages
10.12677/AAM.2016.52022
On the Low-Lou Approach for the Nonlinear Force-Free Magnetic Field
Jian Qin, Yiwei Li
School of Applied Sciences, Taiyuan University of Science and Technology, Taiyuan Shanxi

Received: Apr. 15th, 2016; accepted: May 2nd, 2016; published: May 5th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Nonlinear force-free magnetic field is an important mathematical model in astrophysics, which is a set of nonlinear partial differential equations, often used in the theoretical studies of solar and stellar magnetic fields. In the axisymmetric case, this set of partial differential equations is reduced into a nonlinear ordinary differential equation of second order with an unknown parameter, satisfying certain boundary condition. This is the so-called Low-Lou approach of the problem. In this paper, we propose a parametric shooting method as a technical supplement for the Low- Lou approach, offering more optional numerical force-free magnetic fields.
Keywords:Nonlinear Differential Equations, Shooting Method, Force-Free Field

非线性无力场的Low-Lou解法探讨
秦剑,李毅伟
太原科技大学应用科学学院,山西 太原

收稿日期:2016年4月15日;录用日期:2016年5月2日;发布日期:2016年5月5日

摘 要
非线性无力场是天体物理中的重要数学模型,它是一套非线性偏微分方程组,经常用于太阳及恒星磁场的理论研究。在轴对称情形下,该方程组归化为满足特定边界条件的带有未知参数的二阶非线性常微分方程,此即所谓的Low-Lou解法。本文提出一种参数打靶法,作为对Low-Lou解法的探讨和补遗,并给出更多可选的数值无力场。
关键词 :非线性微分方程,打靶法,无力场

1. 引言
无力场是天体物理中经常用到的磁场模型,尤其在太阳物理的有关研究中受到极大的关注 [1] 。数学上,无力场是指满足如下方程的向量场:
 (1)
(1)
 (2)
(2)
其中, 是空间位置的标量函数,称作无力因子。当
是空间位置的标量函数,称作无力因子。当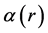 恒为零时,无力场退化为势场,即无电流场;当
恒为零时,无力场退化为势场,即无电流场;当 恒为非零常数时,
恒为非零常数时,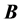 称作线性无力场;当
称作线性无力场;当 恒为非常数时,
恒为非常数时, 称作非线性无力场,此时无力场方程为二阶非线性偏微分方程组,只有少数情况下可以得到一些特解。1990年,Low和Lou [2] 首次给出了一类多极非线性无力场,在天体物理领域获得广泛的关注和应用,详见Wiegelmann和Sakurai的综述文章 [3] 。
称作非线性无力场,此时无力场方程为二阶非线性偏微分方程组,只有少数情况下可以得到一些特解。1990年,Low和Lou [2] 首次给出了一类多极非线性无力场,在天体物理领域获得广泛的关注和应用,详见Wiegelmann和Sakurai的综述文章 [3] 。
在轴对称条件下,任何磁场 都可以在球坐标系中写成如下形式:
都可以在球坐标系中写成如下形式:
 (3)
(3)
其中,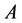 与
与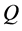 是
是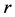 和
和 的函数,与方位角
的函数,与方位角 无关。结合这一条件,Low和Lou将无力场方程转化为如下形式的常微分方程:
无关。结合这一条件,Low和Lou将无力场方程转化为如下形式的常微分方程:
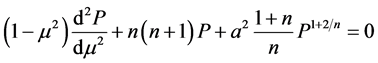 (4)
(4)
其中, 为自变量;
为自变量; 是
是 的函数,也是有待求解的未知函数,满足边界条件
的函数,也是有待求解的未知函数,满足边界条件 。
。
方程(4)是带有未知参数 的二阶非线性常微分方程,Low和Lou将其视作特征值问题进行了“数值研究”,并给出了
的二阶非线性常微分方程,Low和Lou将其视作特征值问题进行了“数值研究”,并给出了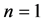 情形下的两组解,但他们在文章中省略了具体的求解过程,由此带来一些困惑,而方程(4)本身的研究也停滞了十多年。直到最近,随着有关研究的深入,非线性无力场的Low-Lou解法才再次引起人们的兴趣 [4] - [7] 。这些进展都是在Low-Lou解法的框架内展开的,由于天体物理领域的作者们侧重于物理内容,求解过程多有省略。迄今为止,对于方程(4)的数值求解,在方法上仍然没有明朗化。本文提出一种参数打靶法,作为对Low-Lou解法的探讨和补遗,并给出更多可选的Low-Lou解。
情形下的两组解,但他们在文章中省略了具体的求解过程,由此带来一些困惑,而方程(4)本身的研究也停滞了十多年。直到最近,随着有关研究的深入,非线性无力场的Low-Lou解法才再次引起人们的兴趣 [4] - [7] 。这些进展都是在Low-Lou解法的框架内展开的,由于天体物理领域的作者们侧重于物理内容,求解过程多有省略。迄今为止,对于方程(4)的数值求解,在方法上仍然没有明朗化。本文提出一种参数打靶法,作为对Low-Lou解法的探讨和补遗,并给出更多可选的Low-Lou解。
2. 参数打靶法
考虑两点边值问题:
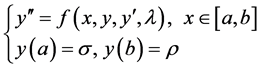 (5)
(5)
其中, 为参数。若
为参数。若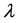 已知,则可以采用通常的打靶法求解该问题。首先将原方程转化为如下的初值问题:
已知,则可以采用通常的打靶法求解该问题。首先将原方程转化为如下的初值问题:
 (6)
(6)
其中, 为
为 在初始点
在初始点 处的斜率。则问题转化为寻找合适的
处的斜率。则问题转化为寻找合适的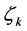 ,使得该初值问题的解满足原边值问题的右端边界条件
,使得该初值问题的解满足原边值问题的右端边界条件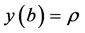 。其次,设相应于
。其次,设相应于 的初值问题(6)的解为
的初值问题(6)的解为 ,并且假定
,并且假定 关于
关于 连续,则要找的
连续,则要找的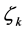 为满足如下方程:
为满足如下方程:
 (7)
(7)
上述方程可用牛顿迭代法求解。
从另一个角度看,数值求解方程(7)的过程,相当于在一定范围内调整 ,使得误差函数
,使得误差函数 的值接近于零。依此观点,当
的值接近于零。依此观点,当 为未知参数时,可以固定
为未知参数时,可以固定 ,然后在一定范围内调整
,然后在一定范围内调整 ,使得误差函数的值接近于零,由此获得原边值问题的数值解。这里的关键在于根据原始边值问题的上下文,选取合适的固定值
,使得误差函数的值接近于零,由此获得原边值问题的数值解。这里的关键在于根据原始边值问题的上下文,选取合适的固定值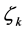 。我们将这种方法称为参数打靶法,见算法2.1。显然,参数打靶法可看作打靶法的变体形式或灵活运用。
。我们将这种方法称为参数打靶法,见算法2.1。显然,参数打靶法可看作打靶法的变体形式或灵活运用。
笔者注意到,最近杨旦旦等人 [8] 也表述了一种处理未知参数的打靶法,并用于火箭和卫星中的液体燃料晃动问题的求解。本文提出的参数打靶法,主要是针对特征值(或参数值)不唯一的情形。特别地,我们首先在打靶区间内获得完整的误差函数曲线,然后一次性求出该曲线的所有零点,可有效地防止“漏算”的情况发生。
3. 算例及分析
为了便于对照Low和Lou的原始结果,我们考虑方程(4)中 的情形,即
的情形,即
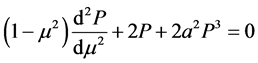 (8)
(8)
其中,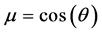 为自变量;
为自变量; 是
是 的函数,满足边界条件
的函数,满足边界条件 。特别地,Low和Lou将此方程作为特征值问题求解,其中
。特别地,Low和Lou将此方程作为特征值问题求解,其中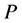 看作特征函数,
看作特征函数, 看作特征值。由于方程没有常数项,边界条件又是齐性的,从而特征函数
看作特征值。由于方程没有常数项,边界条件又是齐性的,从而特征函数 允许所谓的自由规范化。固定起见,Low和Lou规定:在
允许所谓的自由规范化。固定起见,Low和Lou规定:在 处,取
处,取 。为了实施参数打靶法,我们需要选定参数的打靶区间,这里令
。为了实施参数打靶法,我们需要选定参数的打靶区间,这里令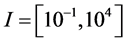 。进一步,在算法2.1中,用
。进一步,在算法2.1中,用 表示
表示 ,取
,取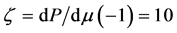 ,
, 。通过试算可知,特征值
。通过试算可知,特征值 的分布越来越稀疏。为了获得精确结果,可将打靶区间分为若干段,逐段实施参数打靶法;计算结果参见图1及表1。注意,特征值的实际分布是越来越稀疏的,所以图1的横坐标采用了对数坐标。表1中给出了打靶区间内的所有特征值,共有19个。Low和Lou在原始文章中给出了该序列的前两个值,他们给出的数值是0.425和2.55。
的分布越来越稀疏。为了获得精确结果,可将打靶区间分为若干段,逐段实施参数打靶法;计算结果参见图1及表1。注意,特征值的实际分布是越来越稀疏的,所以图1的横坐标采用了对数坐标。表1中给出了打靶区间内的所有特征值,共有19个。Low和Lou在原始文章中给出了该序列的前两个值,他们给出的数值是0.425和2.55。
上述结果对应的参数设置如次:以1000的倍数作为分段点,将区间 分为相应的10个
分为相应的10个
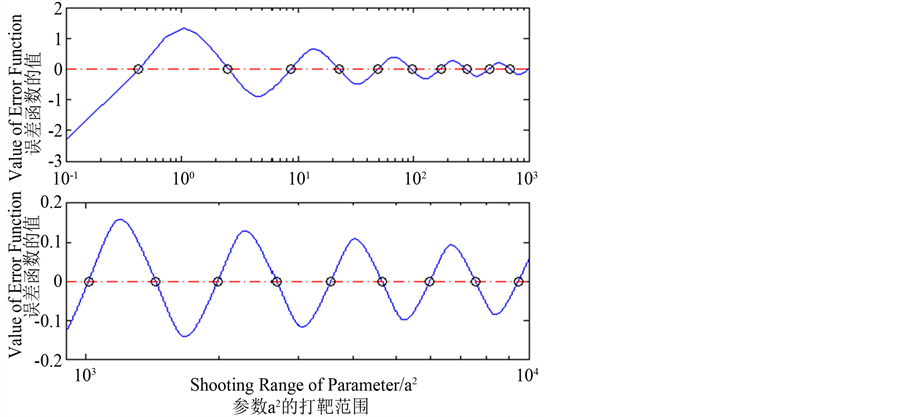
Figure 1. Variation of the error function in the shooting range of 10−1~104 for a2
图1. 误差函数在参数a2的打靶范围10−1~104内的变化曲线
Table 1. Eigenvalues defined by Low-Lou equation in the range of 0.1~10,000
表1. Low-Lou方程定义的特征值在0.1~10,000的数值结果
片段;每个片段均匀地插入3200个节点(含端点),即 ,作为参数
,作为参数 的“打靶点”;用龙格库塔方法求解初值问题时,特征函数
的“打靶点”;用龙格库塔方法求解初值问题时,特征函数 的定义区间插入1999个节点。这些参数是通过试算确定的。下文结合物理背景验证和分析上述计算结果的正确性。
的定义区间插入1999个节点。这些参数是通过试算确定的。下文结合物理背景验证和分析上述计算结果的正确性。
获得特征值后,可用龙格库塔方法计算对应的特征函数。特别地,Low-Lou给出了 和
和 的表达式:
的表达式: ,
,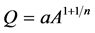 。这意味着,只要得到特征值和特征函数,就可以按照公式(3)计算出空间任一点处的无力场
。这意味着,只要得到特征值和特征函数,就可以按照公式(3)计算出空间任一点处的无力场 。由于特征函数由数值方法得到,故而Low-Lou解法给出的无力场也称作“半解析解”。特别地,Wheatland等人 [9] 给出了衡量数值无力场的精确性的两个指标
。由于特征函数由数值方法得到,故而Low-Lou解法给出的无力场也称作“半解析解”。特别地,Wheatland等人 [9] 给出了衡量数值无力场的精确性的两个指标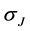 和
和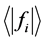 ,分别用于衡量数值磁场满足无力条件和无散条件的程度,其中“
,分别用于衡量数值磁场满足无力条件和无散条件的程度,其中“ ”表示所有数据取平均值。这两个指标是无量纲的标量,具体计算公式如下:
”表示所有数据取平均值。这两个指标是无量纲的标量,具体计算公式如下:
 (9)
(9)
Table 2. Force-free and divergence-free merits for the Low-Lou solutions
表2. Low-Lou解的无力指标与无散指标
 (10)
(10)
其中, 表示节点
表示节点 附近小区域的体积,
附近小区域的体积,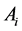 为该区域的表面积,
为该区域的表面积, 表示节点
表示节点 处的电流,
处的电流,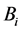 和
和 分别表示节点
分别表示节点 处磁场和电流的大小。
处磁场和电流的大小。
注意,(9)中的 本身是一种平均值,而(10)式中的
本身是一种平均值,而(10)式中的 是指节点
是指节点 处的局部值,由于数值磁场通常分布在立方网格的节点上,为此采用平均值
处的局部值,由于数值磁场通常分布在立方网格的节点上,为此采用平均值 来衡量数值磁场整体上满足无散条件的程度。本文采用Li等人 [10] 编写的程序计算这两个指标。在适当分辨率下,数值无力场的指标
来衡量数值磁场整体上满足无散条件的程度。本文采用Li等人 [10] 编写的程序计算这两个指标。在适当分辨率下,数值无力场的指标 和
和 应当分别达到(或小于)
应当分别达到(或小于) 和
和 的量级水平 [11] 。对应于表1所给的19个特征值,我们计算了相应的特征函数,并按公式(3)计算出19个Low-Lou解。计算中,我们统一采用立方网格
的量级水平 [11] 。对应于表1所给的19个特征值,我们计算了相应的特征函数,并按公式(3)计算出19个Low-Lou解。计算中,我们统一采用立方网格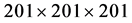 ,计算区域为
,计算区域为 。表2给出了这19个Low-Lou解的无力指标与无散指标。可以看到,两组指标都达到了满意的精度水平。特别地,对于序数较大的特征值,相应特征函数的零点增多,导致磁场结构更复杂,因而指标也略大。
。表2给出了这19个Low-Lou解的无力指标与无散指标。可以看到,两组指标都达到了满意的精度水平。特别地,对于序数较大的特征值,相应特征函数的零点增多,导致磁场结构更复杂,因而指标也略大。
4. 探讨与展望
非线性无力场是天体物理研究中的重要研究课题,而Low-Lou解法给出了求解轴对称非线性无力场的统一框架,它将问题转化为满足特定边界条件的带有未知参数的二阶非线性常微分方程。由于Low和Lou在原始文章中省略了技术细节,导致有关研究长期止步于最初求得的两组特解。本文提出的参数打靶法,能够有效地计算指定范围内的所有特征值,进而获得相应的数值无力场,可作为Low-Lou解法的补遗。需要指出的是,对于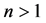 的情形,由于特征函数具有交叉型零点(zero-crossings),方程(4)的非线性项会导致复数的出现,其物理意义不明显。为此,Flyer等人 [4] 考虑了方程(4)的变体形式,而Prasad等人 [7] 则引入了某种变换,兹不赘述。就
的情形,由于特征函数具有交叉型零点(zero-crossings),方程(4)的非线性项会导致复数的出现,其物理意义不明显。为此,Flyer等人 [4] 考虑了方程(4)的变体形式,而Prasad等人 [7] 则引入了某种变换,兹不赘述。就 的情形而言,可以验证,当特征值很大时,相应的数值无力场具有更复杂的几何与拓扑结构,预期可用于模拟太阳物理中的日珥和冕洞等重要物理现象。
的情形而言,可以验证,当特征值很大时,相应的数值无力场具有更复杂的几何与拓扑结构,预期可用于模拟太阳物理中的日珥和冕洞等重要物理现象。
文章引用
秦剑,李毅伟. 非线性无力场的Low-Lou解法探讨
On the Low-Lou Approach for the Nonlinear Force-Free Magnetic Field[J]. 应用数学进展, 2016, 05(02): 166-171. http://dx.doi.org/10.12677/AAM.2016.52022
参考文献 (References)
- 1. Régnier, S. (2013) Magnetic Field Extrapolations into the Corona: Success and Future Improvements. Solar Physics, 288, 481-505. http://dx.doi.org/10.1007/s11207-013-0367-8
- 2. Low, B.C. and Lou, Y.Q. (1990) Modeling Solar Force-Free Magnetic Fields. Astrophysical Journal, 352, 343-352. http://dx.doi.org/10.1086/168541
- 3. Wiegelmann, T. and Sakurai, T. (2012) Solar Force-Free Magnetic Fields. Living Reviews in Solar Physics, 9, 1-49. http://dx.doi.org/10.12942/lrsp-2012-5
- 4. Flyer, N., Fornberg, B., Thomas, S. and Low, B.C. (2004) Magnetic Field Confinement in the Solar Corona. I. Force- Free Magnetic Fields. The Astrophysical Journal, 606, 1210-1222. http://dx.doi.org/10.1086/383025
- 5. Zhang, M., Flyer, N. and Low, B.C. (2012) Magnetic Helicity of Self-Similar Axisymmetric Force-Free Fields. The Astrophysical Journal, 755, 78-87. http://dx.doi.org/10.1088/0004-637X/755/1/78
- 6. Lerche, I. and Low, B.C. (2014) A Nonlinear Eigenvalue Problem for Self-Similar Spherical Force-Free Magnetic Fields. Physics of Plasmas, 21, Article ID: 102902. http://dx.doi.org/10.1063/1.4897366
- 7. Prasad, A., Mangalam, A. and Ravindra, B. (2014) Separable Solutions of Force-Free Spheres and Applications to Solar Active Regions. The Astrophysical Journal, 786, 81-104. http://dx.doi.org/10.1088/0004-637X/786/2/81
- 8. 杨旦旦, 岳宝增, 祝乐梅, 宋晓娟. 用打靶法求解微重力下矩形和旋转对称贮箱内静液面形状[J]. 空间科学学报, 2012, 32(1): 85-91.
- 9. Wheatland, M.S., Sturrock, P.A. and Roumeliotis, G. (2000) An Optimization Approach to Reconstructing Force-Free Fields. The Astrophysical Journal, 540, 1150-1155. http://dx.doi.org/10.1086/309355
- 10. Li, Y., Song, G. and Li, J. (2009) A Test on Two Codes for Extrapolating Solar Linear Force-Free Magnetic Fields. Solar Physics, 260, 109-124. http://dx.doi.org/10.1007/s11207-009-9431-9
- 11. Schrijver, C.J., DeRosa, M.L., Metcalf, T.R., et al. (2006) Nonlinear Force-Free Modeling of Coronal Magnetic Fields Part I: A Quantitative Comparison of Methods. Solar Physics, 235, 161-190. http://dx.doi.org/10.1007/s11207-006-0068-7
