Advances in Applied Mathematics
Vol.06 No.07(2017), Article ID:22374,8
pages
10.12677/AAM.2017.67098
A Method of Obtaining a Priority Vector from Interval Multiplicative Reciprocal Matrices
Zulin Liu, Fang Liu, Yuhao Wu
School of Mathematics and Information Science, Guangxi University, Nanning Guangxi
Received: Sep. 30th, 2017; accepted: Oct. 14th, 2017; published: Oct. 19th, 2017

ABSTRACT
A new method of obtaining a priority vector from interval multiplicative reciprocal matrices is proposed in the present paper. By considering the randomness experienced by decision makers in pairwise comparisons, the cosine maximization method is extended to interval multiplicative reciprocal matrices with approximation-consistency. A new algorithm is proposed to solve the decision making problem with the interval-valued judgements. Numerical results are reported to show the application of the proposed method.
Keywords:Interval Multiplicative Reciprocal Matrix, Priority Vector, Cosine Maximization Method, Approximation-Consistency
区间互反判断矩阵权重确定的一种新方法
刘祖林,刘芳,吴宇豪
广西大学数学与信息科学学院,广西 南宁
收稿日期:2017年9月30日;录用日期:2017年10月14日;发布日期:2017年10月19日

摘 要
本文研究了一种从区间互反判断矩阵中获得权重的新方法,考虑决策者在两两比较方案的判断中存在的随机性,把余弦最大化方法推广到研究近似一致性区间互反判断矩阵,给出了一种求解区间互反判断矩阵决策问题的新算法,数值结果阐明了新方法的应用。
关键词 :区间互反判断矩阵,权重,余弦最大方法,近似一致性

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在复杂的决策环境中,由于决策者主观思维的模糊性和决策因素的不确定性,决策者可能给出区间数互反判断矩阵表示他们对方案的偏好关系。近年来许多学者对区间数互反判断矩阵进行了相关的研究 [1] [2] [3] [4] 。基于层次分析法 [5] ,因为决策者受相关经验和决策知识的约束,通常很难给出一致的互反判断矩阵。为了得到合理和可靠的权重,需要对决策者提供的判断矩阵进行一致性检验。比如文献 [6] 中采用有限迭代的方法对其进行修正,使其满足满意一致性。而对于区间互反判断矩阵的一致性问题更加复杂并存在一些争论,最近,文献 [7] 对区间互反判断矩阵的一致性定义进行了述评,并指出区间互反判断矩阵本质上是不一致的,只能考虑包含在其中的有限理性,提出了近似一致性的新概念。
从区间数互反判断矩阵中获得合理的权重向量是决策分析中一个重要的问题,许多的学者已进行了相关的研究并提出了许多方法 [2] [3] [4] [7] [8] 。基于近似一致性的新概念 [7] ,有必要研究从区间数互反判断矩阵获得权重的新方法。本文利用余弦相似测度方法确定由区间数互反判断矩阵端点构成的两互反判断矩阵的权重,然后通过凸组合技术得到相应区间数互反判断矩阵的权重。最后考虑决策者比较方案时的随机性,得到区间数权重,给出了新算法并得出方案的排序或择优。
2. 预备知识
设 表示一组决策方案,经典层次分析法中 [5] ,决策者通过互反判断矩阵表示两两比较的偏好矩阵 ,其中元素 表示任意方案 与 的比值,且 。当 时,表示方案 完全优于方案 ;当 时,表示方案 完全优于方案 ;当 时,表示方案 与 无差异。相对测度下,有 ,且 时, 称作互反判断矩阵,其一致性定义如下:
定义2.1 [5] :若互反判断矩阵 满足 , ,那么称矩阵 为一致性互反判断矩阵。
当判断矩阵 是不一致时,文献 [5] 进一步定义了一致性指标( )和一致性率( )对 的不一致性程度进行量化:
, (1)
其中 和 分别表示矩阵 的维数和最大特征值, 表示随机产生的互反判断矩阵的平均一致性指标。当 时, 为一致的互反判断矩阵;当 时,互反判断矩阵是满意的;当 时,互反判断矩阵是不满意的并且有必要修正为满意一致性。另外,基于余弦相似测度,文献 [9] 提出了一种新的一致性指标( ):
, (2)
其中 和 分别表示互反判断矩阵 的权重向量和第 列向量,且 , , 。当 时,称矩阵 为一致性互反判断矩阵。一般来说, 时,矩阵 是满意的 [9] 。
在复杂的决策环境中,为了更加合理的表示模糊环境中决策者对方案的偏好关系,在文献 [1] 中,考虑用区间数来表示任意两个方案的偏好比值,从而构造出一个区间数互反判断矩阵。进一步,考虑决策者两两比较的随机性,文献 [7] 中考虑了任意方案 的排列 ,得到相应的区间数互反判断矩阵形式如下:
其中 表示方案 比方案 的优越程度在 和 之间。满足 , ,且 。
从区间数互反判断矩阵 中构造的两个实互反矩阵判断矩阵 和 如下:
, (3)
假设
(4)
其中 , 。
定义2.2 [7] :若存在一个排列 使得互反判断矩阵 和 具有一致性,那么区间数互反判断矩阵 是近似一致性的。
定义2.3 [7] :若存在一个排列 使得互反判断矩阵 和 具有满意一致性,那么 称为具有满意近似一致性的区间数互反判断矩阵。
定理2.1 [7] :若区间数互反判断矩阵 为满意近似一致性,当且仅当存在一个排列 使得互反判断矩阵 为满意一致性。
以上定义是根据经典层次分析法中的一致性指标给出的,采用 指标,我们给出区间互反判断矩阵近似满意一致性的新定义,即
定义2.4:若存在一个排列 使得互反判断矩阵 和 的 等于或大于90%,那么称区间数互反判断矩阵 是满意近似一致性的。
基于定义2.4,可以证明定理2.1同样成立,下面考虑当区间数互反判断矩阵满足定义2.4的条件时区间数权重确定的新方法。
3. 区间数权重确定新方法
下面把从互反判断矩阵中获得权重的余弦最大化方法推广到区间互反判断矩阵,建立从区间互反判断矩阵获得权重的新方法,并考虑决策者两两比较方案的随机性,给出备选方案的区间数权重。
根据定义2.4可知,讨论区间数互反判断矩阵 的近似一致性,只需对(3)式构成的互反判断矩阵进行讨论。首先,我们利用 一致性指标判断 和 是否满意,若两者同时通过了检验,则表明判断矩阵 具有满意近似一致性。否则,需要对它们进行修正。根据文献 [9] 的定理2,令
, (5)
那么得到关于互反判断矩阵 和 的优先权重如下:
(6)
(7)
根据(4)式,令
(8)
则
(9)
当 时,则 ;当 时,则 。当 时,对于区间数互反判断矩阵 中任意一个排列,那么
(10)
因此,从区间数互反判断矩阵 获得的区间数权重为:
(11)
考虑决策者判断的随机性,采用均值估计决策方案的权重 [7] 为:
(12)
特别的,当区间互反判断矩阵 是近似一致性时,有如下定理:
定理3.1:假设区间数互反矩阵 是近似一致性,则存在一个排列 使得区间数权重(11)可以简化为
. (13)
证明:由于 是近似一致性的,则存在一个排列 使得由(4)构造的判断矩阵 是一致的。
假设 为判断矩阵 的权重向量,由文献 [9] 中的定理2可知,
, , , .
由(4)式得
.
当 时,则
,
当 时,有
.
当 时,则
很显然,上式可以改写成如下形式:
4. 算法与数例
基于区间数权重确定新方法,下面给出区间数互反判断矩阵的决策问题新算法。
Step 1:假设 表示一组有限方案,由方案两两比值构成相应的区间数互反判断矩阵 ,并利用(3)式从 中构造两个实互反矩阵 和 。
Step 2:利用(2)式检验 和 ,若存在一个排列 使得两者是满意一致的,则直接执行Step 6,否则继续执行下一步。
Step 3:首先利用(3)式获得 或 的权重向量 。然后利用欧几里得距离获得 和 中的元素与其对应权重的平均偏差值:
并确定 和 的偏差矩阵 。
Step 4:令 ,那么
Step 5:改变下标 和 的值,返回Step 2。
Step 6:应用(12)式获得区间数互反判断矩阵 权重向量。
Step 7:利用文献 [3] 的可能度公式确定相应的可能度矩阵 。
Step 8:利用文献 [2] 中的行列消去法可获得方案权重的排序。
Step 9:结束。
下面给出数例说明新方法的应用。设区间数互反判断矩阵如下:
考虑区间数互反判断矩阵 的所有排列如表1所示。根据定义2.4可知,区间数互反判断矩阵 是非一致的。此时,我们选择置换 进行修正。
,
从表1得 , 。显然判断矩阵 是非一致的, 是满意一致的。根据定理2.1,我们只需对判断矩阵 进行修正。根据Step 3可得判断矩阵 的元素与其对应权重的欧几里得平均偏差 ,对应的偏差矩阵为
很显然元素 需要修正。令 ,修正后的矩阵为:
对应 。此时对应的判断矩阵 仍是非一致的。重复上述过程可获得满意一致性矩阵为:
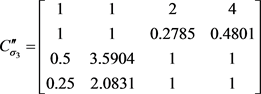
Table 1. CCI indexes of C 2 σ and D 2 σ
表1. 和 的CCI指标
其中 ,根据定义2.3可知,区间数互反判断矩阵 具有满意近似一致性。
利用(11)式可得
。
根据可能度公式获得相应的可能度矩阵为 [5] :
运用简单的行列消去法得到权重的优先级 。
5. 结论
本文基于互反判断矩阵不一致性程度测量的CCI指标,定义了区间互反判断矩阵的满意近似一致性. 采用余弦最大化方法,给出了区间互反判断矩阵的权重确定方法,进一步考虑决策者两两比较备选方案时表现的随机性,获得了从区间数互反判断矩阵的备选方案的权重,最后给出算法和数例并阐明了方法的应用。
基金项目
国家自然科学基金项目(71571054, 71201037),广西自然科学基金(2016GXNSFFA380004),广西大学科研基金(XBZ160257)。
文章引用
刘祖林,刘芳,吴宇豪. 区间互反判断矩阵权重确定的一种新方法
A Method of Obtaining a Priority Vector from Interval Multiplicative Reciprocal Matrices[J]. 应用数学进展, 2017, 06(07): 808-815. http://dx.doi.org/10.12677/AAM.2017.67098
参考文献 (References)
- 1. Saaty, T.L. and Vargas, L.G. (1987) Uncertainty and Rank Order in the Analytic Hierarchy Process. European Journal of Operational Research, 32, 107-117.
- 2. Wang, Y.M., Yang, J.B. and Xu, D.L. (2005) A Two-Stage Logarithmic Goal Programming Method for Generating Weights from Interval Comparison Matrices. Fuzzy Sets and Systems, 152, 475-498.
- 3. Liu, F. (2009) Acceptable Consistency Analysis of Interval Reciprocal Comparison Matrices. Fuzzy Sets and Systems, 160, 2686-2700.
- 4. Xia, M.M. and Chen, J. (2015) Studies on Interval Multiplicative Preference Relations and Their Application to Group Decision Making. Group Decision and Negotiation, 24, 115-144. https://doi.org/10.1007/s10726-014-9383-9
- 5. Saaty, T.L. (1980) The Analytic Hierarchy Process. McGraw-Hill, New York.
- 6. Xu, Z.S. and Wei, C.P. (1999) A Consistency Improving Method in the Analytic Hierarchy Process. European Journal of Operational Research, 116, 443-449.
- 7. Liu, F., Pedrycz, W. and Zhang, W.G. (2017) Limited Ra-tionality and Its Quantification through the Interval Number Judgments with Permutations. IEEE Transactions on Cybernetics. (In Press)
- 8. Meng, F, Chen, X., Zhu, M. and Lin, J. (2015) Two New Methods for Deriving the Priority Vector from Interval Mul-tiplicative Preference Relations. Information Fusion, 26, 122-135.
- 9. Kou, G. and Lin, C. (2014) A Cosine Maximization Method for the Priority Vector Derivation in AHP. European Journal of Operational Research, 235, 225-232.
