Pure Mathematics
Vol.
13
No.
05
(
2023
), Article ID:
66336
,
7
pages
10.12677/PM.2023.135139
G-期望框架下G-Lévy过程的Black-Scholes公式
郑红,李洋
上海理工大学理学院,上海
收稿日期:2023年4月21日;录用日期:2023年5月22日;发布日期:2023年5月29日

摘要
随着金融市场的蓬勃发展,Black-Scholes公式得到了广泛研究,我们考虑在G-期望框架下,对于G-布朗运动和G-跳过程共同驱动的线性随机微分方程,由G-伊藤公式和泰勒公式,严格得到了Black-Scholes公式并给出了证明。
关键词
Black-Scholes方程,G-期望,G-Lévy过程,G-伊藤公式

Black-Scholes Formula for G-Lévy Process under G-Expectation Framework
Hong Zheng, Yang Li
College of Science, University of Shanghai for Science and Technology, Shanghai
Received: Apr. 21st, 2023; accepted: May 22nd, 2023; published: May 29th, 2023

ABSTRACT
With the rapid development of the financial market, Black-Scholes formula has been widely studied. We consider that under the G-expectation framework, for the linear stochastic differential equation driven by G-Brownian motion and G-jump process, the Black-Scholes formula is strictly obtained and proved by G-Ito formula and Taylor formula.
Keywords:Black-Scholes Equation, G- Expectation, G-Lévy Process, G-Ito Formula

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在过去的30年里,随机过程在数学金融的应用中得到了广泛的研究,除了随机过程的随机性外,还具有波动不确定性,这意味着波动率不是精确已知的,2007年,Peng [1] 引入了特殊的新的次线性期望——G-期望,G-期望是由生成元函数为G的非线性抛物型偏微分方程的解定义的,他在G-期望框架下定义了G-正态分布和G-布朗运动,G-布朗运动非平凡地推广了经典运动。简而言之,G-布朗运动是在给定次线性期望下,具有独立且平稳增量的连续过程,可来模拟这种波动不确定性。自2007以来,G-期望和G-布朗运动相关理论取得了重大进展。2008年,Peng [2] 证明了次线性期望下的大数定律和中心极限定理,并定义了关于G-布朗运动的伊藤积分。之后,Peng [3] 得到了G-伊藤公式,证明了G-布朗运动驱动的随机微分方程(简称G-SDEs)和G-布朗运动驱动的倒向随机微分方程(简称G-BSDEs)解的存在唯一性。此后,G-期望空间和G-伊藤积分的应用得到了许多研究者的广泛研究。Yang和Zhao [4] 介绍了G-期望下的G-布朗运动和G-正态分布的模拟,Chai [5] 研究了G-框架下随机微分方程的期权定价问题。虽然G-布朗运动解决了许多金融问题,但一些依赖莱维过程的金融模型仍然没有解决。因此,Peng和Hu [6] 研究了G-莱维过程,这是G-布朗运动的推广。Krzysztof [7] 对G-莱维过程引入了G-伊藤公式和G-鞅表示。王 [8] 研究了G-期望下的G-Jensen不等式。王 [9] 研究比较定理与G-期望下的亚洲期权定价。康 [10] 研究了G-期望下的布朗运动鞅表示定理。
20世纪70年代,随着金融市场的飞速发展,金融领域的定价问题广泛引起人们的兴趣。而期权定价问题的研究更是受人关注,特别是Black和Scholes得出欧式看涨期权的显示解。布莱克–斯科尔斯定价公式得到广泛应用,但是定价公式本身的一些假设与现实存在一定出入。随后,著名的布莱克–斯科尔斯公式受到了许多学者的重视。1976年,在假设利率为常数的条件下,Merton [11] 提出了股票价格的对数跳扩散模型,该模型被描述为布朗运动和复合泊松过程的结合。自此,关于带跳扩散的其它期权方面的研究也屡见不鲜。而随着G-期望的迅速发展,G-框架下的欧式期权定价公式也得到了众多学者的关注,2010年,Xv [12] 等人给出了G-几何布朗运动描述的资产价格变动,得到了欧式看涨期权定价公式。2014年,Lu和Liu [13] 利用G-几何布朗运动描述的资产价格变动,进而得到G-框架下的欧氏幂期权的定价公式。2021年,Xin和Zheng [14] 给出了G-莱维下的布莱克–斯科尔斯定价公式,并给出相关模拟。关于G-期望下的数值模拟的更多细节可参考 [15] 及其参考文献。
本文主要对G-期望下的相关理论做了进一步的研究,我们考虑股票价格 ,令:
其中 是利率, 是波动率, 是资产价格的跳跃范围,在G-框架下, 是G-布朗运动, 是G-Lévy过程。
本文其它部分构成如下:在第二节中,我们给出G-期望框架下的相关概念,第三节中我们对G-Lévy过程下提出的Black-Scholes方程定理,并进行证明,最后,我们对我们的成果进行了总结。
2. 预备知识
G-随机分析
本章中,主要给出G-随机分析的一些基本相关知识,设 为给定集合,设 为 上定义的实值函数的线性空间,假设对于任意的常数C满足 ,如果 ,则 ,空间 被看作是一个随机变量组成的线性空间。
定义2.1.1 [3] (次线性期望)一个非线性期望 是定义在随机变量空间 上,并满足以下条件的一个泛函
单调性: ,如果 且 。
保常性: 。
次可加性: , 。
正齐次性: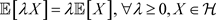 。
。
被称为次线性期望空间。
定义2.1.2 [3] (分布函数)设 。在 上设 :
其中 ,我们称 为随机变量X的分布函数。
定义2.1.3 [3] (同分布)设 和 ,当且仅当
记作 。
定义2.1.4 [3] (相互独立)设 , ,称X与Y独立,当且仅当
定义2.1.5 [3] (G-正态分布)在 上,记随机变量X服从标准G-正态分布,其中 ,若满足
这里 是独立于X的随机变量. 其中 ,并且 。
这里字母G表示函数
其中是单调的线性泛函, 表示由d维对称矩阵构成的集合,则存在有界闭凸子集 ,使得
下面我们给出G-布朗运动的定义。
定义2.1.6 [3] (G-布朗运动)设 是定义在 上的一个d维过程,满足下列性质
1) ;
2) , 和 是同分布的, 独立于 , ;
3) 和 ;
则 为G-布朗运动。
注:记新的G-布朗运动 ,其中 ,
定义2.1.7 [3] (G-Lévy过程)设 为次线性期望空间 上的d维可料过程。如果 满足以下性质,则称 为G-Lévy过程。
;
独立增量: ,增量 是独立的;
平稳增量:增量 的分布是稳定的,不依赖于t;
对于每个 , , 是个连续过程, 是个跳过程;
两个过程 和 满足以下条件 , ,对所有的 。
引理2.1.1 [3] (G-伊藤公式)假设 是m维G-布朗运动。设 是有界的,导数也是有界的,并且 是一致的Lipschitz函数。 是给定的, 是 的第i个分量
其中 是 的第i个元素, 和 分别是是 和 的第i行、第j列元素。设 是m维G-布朗运动和 是G-Lévy跳过程,我们有
3. G-Lévy过程下的Black-Scholes公式
在本节中,我们考虑以下股票价格 ,使:
(1)
其中 是利率系数, 是波动率系数, 是资产价格的跳跃系数, 是G-布朗运动, 是G-框架下的G-Lévy过程。
在本小节中,将结合G-伊藤公式和泰勒公式,证明得到G-Lévy过程下的Black-Scholes偏微分方程。
定理3.1 (Black-Scholes公式):假设 是期权价格, 是股票价格。对于式(1),我们可以得到G-Lévy过程下的积分偏微分方程(integral-PDE)过程
其中 , 。
证明:我们在 上定义时间分割, , 。令函数 是足够光滑的, 和 ,利用G-伊藤公式,可以得到式(1)的显式解:
(2)
在G-期望空间中,我们有以下乘积法则:
那么,期权定价公式如下形式:
(3)
接下来,我们介绍G-Lévy过程下的布莱克–斯科尔斯模型。用泰勒公式对 进行展开,我们有
(4)
将式(2)代入式(4)可得
(5)
其中
对 在 处进行泰勒展开得
由 的泰勒展开和(5)可得
因为对 ,我们有
所以
将上式代入方程(3),我们可得
将上式代入(5)得
其中 和 是无风险利率,根据G-期望的性质和 和 ,可得
其中 .由此,得到积分偏微分方程:
定理即证。
4. 总结
本文考虑在G-期望框架下,利用G-伊藤公式和G-期望等性质,对于G-布朗运动和G-莱维过程共同驱动的线性随机微分方程,严格得到了Black-Scholes公式并给出了证明,和从传统的期权定价公式相比较,考虑在更一般的非线性期望(G-期望)理论下,能够更好的描述复杂的金融市场,利用G-伊藤公式和Taylor公式,结合G-Lévy过程(G-布朗运动和G-跳过程)的随机分析理论,得到G-布朗运动和G-跳过程共同驱动的随机微分方程的Black-Scholes公式,对于后续在金融期权等相关领域具有重要的研究意义和应用价值。
文章引用
郑 红,李 洋. G-期望框架下G-Lévy过程的Black-Scholes公式
Black-Scholes Formula for G-Lévy Process under G-Expectation Framework[J]. 理论数学, 2023, 13(05): 1363-1369. https://doi.org/10.12677/PM.2023.135139
参考文献
- 1. Peng, S. (2007) G-Expectation, G-Brownian Motion and Related Stochastic Calculus of Itô Type. In: Benth, F.E., Di Nunno, G., Lindstrøm, T., Øksendal, B. and Zhang, T., Eds., Stochastic Analysis and Applications, Abel Symposia, Vol. 2, Springer, Berlin, 541-567. https://doi.org/10.1007/978-3-540-70847-6_25
- 2. Peng, S. (2008) A New Central Limit Theorem under Sublinear Expectation. (Preprint)
- 3. Peng, S. (2010) Nonlinear Expectations and Stochastic Calculus under Uncertainty: With Robust CLT and G-Brownian Motion. Springer, Berlin.
- 4. Yang, J. and Zhao W. (2016) Numerical Simulations for G-Rownian Motion. Frontiers of Mathematics in China, 11, 1625-1643. https://doi.org/10.1007/s11464-016-0504-9
- 5. Chai, C. (2019) Application of G-Brown Motion in the Stock Price. Journal of Mathematical Finance, 10, 27-34. https://doi.org/10.4236/jmf.2020.101003
- 6. Hu, M. and Peng, S. (2009) G-Lévy Processes under Sublinear Expectations. (Preprint)
- 7. Krzysztof, P. (2012) Itô Calculus and Jump Diffusions for G-Lévy Processes. (Pre-print)
- 8. Wang, W. (2009) Properties of G-Convex Function under the Framework of G-Expectations. Journal of Shandong University, 44, 43-46.
- 9. Wang, Y. (2018) Research of the Comparison Theorem and Asian Option Pricing under the G-Expectation. Master’s Thesis, Nanjing University of Science and Technology, Nanjing.
- 10. Kang, Y. (2012) Brownian Motion Martingale Representation Theorem under the G-Expectation. Master’s Thesis, Northwest Normal University, Lanzhou.
- 11. Merton, R.C. (1976) Option Pricing When Underlying Stock Returns Are Discon-tinuous. Journal of Financial Economics, 3, 125-144. https://doi.org/10.1016/0304-405X(76)90022-2
- 12. 刘莹莹. 由G-布朗运动驱动的某些欧式期权的定价及相关问题[D]: [硕士学位论文]. 上海: 东华大学, 2014.
- 13. 陆允生, 刘莹莹. 由G-布朗运动驱动的某些欧式期权的定价[J]. 苏州科技学院学报(自然科学版), 2014, 31(3): 6-9+23.
- 14. Xin, Y. and Zheng, H. (2021) Black-Scholes Model under G-Lévy Process. Journal of Applied Mathe-matics and Physics, 9, 3202-3210. https://doi.org/10.4236/jamp.2021.912209
- 15. Yang, J. and Zhao, W. (2016) Numerical Simulations for the G-Brownian Motion. Frontiers of Mathematics in China, 11, 1625-1643. https://doi.org/10.1007/s11464-016-0504-9