求解一类凸多目标规划最小弱有效解的填充函数法 A Filled Function Method of Finding Weak Efficient Mi-nimizer for Convex Multi-Objective Optimization

doi:10.12677/pm.2011.12029

设为首页加入收藏期刊导航网站地图

期刊菜单

文章导航

Pure Mathematics 理论数学, 2011, 1, 149-155

http://dx.doi.org/10.12677/pm.2011.12029 Published Online July 2011 (http://www.hanspub.org/journal/pm/)

A Filled Function Method of Finding Weak Efficient

Minimizer for Convex Multi-objective Optimization*

Ying Zhang, Yingtao Xu

Department of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua

Email: znuzy@shu.edu.cn

Received: Mar. 25th, 2011; revised: Apr. 20th, 2011; accepted: Apr. 23rd, 2011.

Abstract: To a kind of multi-objective optimization problem, which objective function is convex vector

function and which constraints are box sets, firstly we use linear weighted method to turn it into nonconvex

single-objective optimization problem, secondly we get the global minimizer of the single-objective optimi-

zation problem by implying the filled function method, then we attain the weak efficient minimizer of the

prime multi-objective optimization problem.

Keywords: Operations Research; Multi-Objective Programming; Filled Function; Local Minimizer; Global

Minimizer

求解一类凸多目标规划最小弱有效解的填充函数法*

张莹，徐应涛

浙江师范大学数理与信息工程学院，金华

Email: znuzy@shu.edu.cn

收稿日期：2011年3月25日；修回日期：2011年4月20日；录用日期：2011 年4月23日

摘要：针对一类目标函数为凸向量值函数且约束为箱子集的多目标规划，先利用线性加权和法将其转

化为非凸单目标规划，再利用填充函数法求得该单目标规划的全局最优解，从而得到原规划的最小弱有

效解。

关键词：运筹学；多目标规划；填充函数；局部极小点；全局极小点

1. 引言

多目标规划作为最优化的一个重要分支，它主要

研究在某种意义下多个数值目标的同时最优化问题，

是当前计算数学、应用数学以及工程优化中较为活跃

的研究领域之一。近年来，关于多目标规划的研究十

分活跃，如[1-3]，但由其自身的复杂性，针对规划本身

直接求解的研究较少。本文采用间接方法，将多目标

规划转化为单目标规划，再利用填充函数求解。

考虑如下的凸多目标规划问题(VP)：

 





min,,, p

xfxfxfx (1)

..,1, ,

iii

tlxu in





其中函数 :n

RR是凸向量值函数，，

lu 

1, ,in



 。

针对规划(VP)，利用线性加权和法将其转化为如

下单目标规划问题(SP)1：



 

11 22

min pp



xfx f

 

x (2)

..,1, ,

iii

tlxu in





其中



,,,0, 1

pj j













 







.

*基金项目：国家自然科学基金资助项目(No. 11001248)。

张莹等求解一类凸多目标规划最小弱有效解的填充函数法

150 |

引理 1.1[4] 对每个给定的





 ，相应于(SP)1的

最优解必是(VP)的弱有效解。

引理 1.2[4] 对(VP)的任一弱有效解

，都必存在

一个





 ，使

是(SP)1的最优解。

以上两个引理说明，对凸多目标规划来说，当取

遍





 时，通过求(SP)1的最优解便可得到(VP)的弱

有效解集，且(VP)的任一弱有效解

，必存在一个





 ，使

是(SP)1的最优解。因此，(SP)1的全局

最优解一定是(VP)的弱有效解，这个解就称为最小弱

有效解，定义如下：

定义 1.1 如果







是(SP)1的全局最优解，则

称*

是(VP)的最小弱有效解。

但求解(SP)1的全局最优解时，每次需选定一个

，这为(SP)1的求解带来一定的困难。本文

视为变量，令



















 











112 211

(1 )

xfxfx f

 









 







可得如下非凸单目标规划问题(SP)2：



min ,



(3)

..,1, ,

01,1,,

iii

tlxu in



 

 

从而，若





是(SP)2的全局最优解，则 *

是(VP)

的最小弱有效解。

(SP)2是个变量的非凸非线性规划问题，

而填充函数法是一种求解非凸非线性规划全局最优解

的有效方法。利用(SP)2本身的特点并结合填充函数的

优点，本文给出了求解(SP)2全局最优解，即(VP)最小

弱有效解的一类新的填充函数法。

1np

2. 新的填充函数及其性质

2.1. 问题表述

填充函数法最先由葛仁溥[5]提出，是一类较为有

效的确定性全局优化方法。它在当前局部极小点处构

造填充函数，通过极小化填充函数迅速跳出当前局部

极小点达到函数值更小的局部极小点，循环运算直至

找到全局极小点。填充函数法提供了一个利用局部优

化工具解决全局优化问题的方法，因此受到理论及实

际工作者的欢迎，有很多学者对此作了进一步的研究，

如[6-9]。

但这些文献中提出的填充函数，由于参数的选取

与局部极小点的谷域的半径有关且很敏感，计算性能

不理想；并要求目标函数二次连续可微以及局部极小

点的个数有限，但实际应用时目标函数有可能是不可

微或者有无限多个局部极小点。这就促使我们去寻找

具有易调节参数且更好性质的填充函数。

考虑如下的规划问题：



min

x (4)

txS

其中





,1,,

iii

SxRaxbin



，



 ，1,,in



 函数



x是Lipschitz 连

续的且 Lipschitz 常数为L。

记





iii

xax



，1, ,in



 ，



iii

xxb



，

1,,2 nin



 ，则(4)等价于以下问题(P)：



min

x (5)

..st x

其中







0,1,, 2

Rgxin 。记 L(P)为(P)

的所有局部极小点的集合，G(P)为(P)的所有全局极小

点的集合，假设 *

是



x的当前局部极小点，

 









fx

Lx LP fx 是有界闭集，假设(P)

的不同局部极小点的个数可以是无限的，但不同局部

极小值的个数是有限的。

填充函数的最初定义由葛仁溥[5]提出如下：

定义 2.1 函数





,Pxx 被称为



x在点*

处的

填充函数，若





x,Px 满足以下性质：

(P1) *

是





,Pxx

*的严格局部极大点，且





在*

的盆谷是





xx 在山丘的一部分；

(P2) 凡是比 *

的盆谷高的盆谷处，不会有





,Pxx 的局部极小点或平稳点；

(P3) 若存在盆谷低于盆谷，则一定存在

，使得在



和*

连线上存在的局部极

小点。





该填充函数的定义依赖于目标函数





x的盆谷

和山丘的概念，这就需要假设



x仅有有限个极小

点。不利用函数的盆谷和山丘的概念，我们改进填充

函数如下：

张莹等求解一类凸多目标规划最小弱有效解的填充函数法151



定义 2.2 函数



xx 被称为



x在点*

处的

填充函数，若满足以下性质：



,Px



(P1) *

是在的严格局部极大点；



,Pxx n

(P2) 对任意的 *

x 或，有

，这里

xR



0,Pxx





,0,1,,2

Rfxfx gxin 



xx是





xx 在点

处的广义梯度；

(P3) 若





,xf xf xx 非空，则存

在使得

x2

是的局部极小点。



,Pxx



定义 2.2 表明若是满足定义 2.2 的填充函

数且



,Pxx

不是全局极小点，则在极小化





xx 的过程

中，一定会找到

满足







xfx，从

出发利用

局部搜索可达到一个函数值比



x更低的极小点，

从而跳出当前局部极小点，重复此过程直到找到全局

极小点。

2.2. 新的单参数填充函数及其性质

本节提出一个新的单参数填充函数：



min0,max,,1,,2

Pxx

x xfxfx

xfxgxi n







 









其中 *

是



x的当前局部极小点， 是欧几里德范

数。

下面的定理 2.1～2.3 证明



,,Pxx





是满足定义

2.2 的填充函数。

定理 2.1 假设



LP，若 1



，则 *

是



,,Pxx





的严格局部极大点。

证明因为



LP，则存在*

的邻域



,Ox



，10







，使得对任意的，

有



*,x





xO



xfx。下面考虑两种情况：

情况 1：对任意的





,xOx







，有



min 0,max,,1,,20

fxfxgxin







情况 2：对任意的



 

xOx R



\，至少

存在一个





01,, 2in 



使得，则



gx











min 01,,20fx n



,maxfx , ,

gxi







因此，对任意的





,xxO



，*

x，当 1



时，

有







0,,

Pxxxxf xfx

xxLxx

Px x





 

 



则*

是





,,Pxx



的严格局部极大点。

定理 2.2 假设





LP且*

x 或



，当 1





，有



0Pxx



 。

证明考虑如下两种情况：

情况 1：对任意的 *

x ，有







xfx，







，







，。则

1, ,

2in













min 0,max,,1,,20

fxfxgxin









情况 2：对任意的，至少存在一个\

xR





01,, 2in 使得





gx 0，则













min 0,max,,1,,20

fxfxgxin









因此，由













,,Pxxxxf xfx



 *

，

得



,, xx

Pxxf x









记



，有





** *

11 1

,, ,,

110

xxd

Pxx dd

xx xxxx







 







 

 



  



这里







 。因此，对任意的



,,Pxx



 ，有





，即





0,,Pxx



 。





LP但



GP定理 2.3 假设且

张莹等求解一类凸多目标规划最小弱有效解的填充函数法

152 |

intcl cl 。当 1



 且



适当小时，存在点

x 使得*

是P



,,xx





的一个局部极小点。

因*

证明为



LP但



GP，则存在





的另一个局部极小点 *

且







xfx

，





gx 0



，

1,, 2in。因为



x连续

是Lipschitz 的，



,1,

xi

3intx使得

n连续 inl cl ，则存在点

 

且c



fx，1,, 2in。，



0

当1



时，有



 



 



 

*** *

31 3

***

313

***

313

***

313

max,,1,,2

1max,,1,, 2

Px x

x xfx

xfx xin

Lxx

xfx xing

xfxxin



  



 



 



 





 





则。

对任意的，个使

得



因此当



lim,,Px x





x



则

至少存在一



01,, 2in 



ix，



xfx





min 0,ma,,1,,20

fx gin











时，有



***

111

Pxxxxxf x





 



从而

x



适当小时，必有



***

31 1

,, ,,Px xPxx



。

因此







m,,)min,,,,

xxP xxP xx

Px x



in(P







 





且是开集，则当\ 1



 且



适当小时，

x是



,,Pxx

0\ 1



的局部



极点，且由

小



,,Pxx



,,x x



必有

 

xfx，







，1,, 2in





2.4 说明

，即

该填有一个

x

充函数

。

很好的性下面的定理

质,即距离当前局部极小点*

越远，函数值越小，从而

保证在极小化填充函数的过程中不会回到原来的盆

谷，极小点必在目标函数值低于



x的区域得到。

定理 2.4 假设





LP，

11 2



 x ，1

x

2,, 0x



 或



，且







xfx，









xfx若或 2





0min,







 



则









** *

21 1111

,,,,0,,PxxPxxPxx



 



证明对满足条件的1

和2

，易得













111

mi, 20

inn0, max,,1,fxfxgx i





 



和













21 2

min 0,max,,1,,20

fx fxgxin



 



考虑











 



21 11

21 1121

21 11**

21 11

P,, ,,

x xPxx

xxx xfxfx

xx xxLxx

xx xxL

xxx

xx xxL











 









 









 







则当 1

0min,

















时，结合定理 2.1，有









** *

21 1111

,,,,0,,PxxPx xPxx









3. 填充函数算法 NFFM 和数值实验

填充函数算法 NFFM。

摄动常数

3.1. 填充函数算法 NFFM

基于以上讨论，我们给出

初始步

1. 选择一个，例如： :0.1



。



张莹等求解一类凸多目标规划最小弱有效解的填充函数法153

2. 选择参数



的一下界 L0



个，例如：

3. 选个小数



。

择一



ˆ0



，例如：ˆ0.1



.

4. 选择方向 00

e,, ,2

kkkk 里1,2, n，这是变

量的

维数。

5. :1k.

主步

1. 以

为初始点，利用有约束局部搜索程序极小

化原问题(P)，得到



x第一个局部极小点 *

。

2. 令1



。

3. 构造函填充数：



, ,Pxx

min0,max,,1,,2

xxfx fx

xfxgxin



 







4. 若，转步 7；否则以为初始

点，利用无约束局部搜



kk*

:δek

xx

化填充函索程序极小数问题

(F)，得到



,,Pxx



一个局部极小点k

。

(F)





min, ,Pxx



(6)

txR

5. 若，令，转步4；否则下一步。

x:1kk

6. 若k

满足







xf ，令 :k

x

x且:1k



，

以

为新的始点序极小化

原问题(P)，得到



初，利用有约束局部搜索程

x的另一个局部极小点 *

，令

x，转步 2；一步。

减小

否则下



，令 ˆ





。

8. 若



，令，转:1k步3：否则算法停止，

为全局极

个阶段，局部极小化阶段和填充

阶段

1：得到

小点。

注：算法包括两

：

阶段



x的一个局部极小点 *

。

阶段 2：构造



1,Px





且极小化



,Px *



。当

找到满足



x在2

内的fx的且 k

时，算法跳

出阶段2，把 k

并返回阶段 1

作为新的初始点寻找



x的另一个局部极小点*

(果存在的话)。

主步 2中令 1

如

在



，通过以上两阶段循环逐渐减

小直到



小于某个预设值，最后找到的局部极小点被

认为是全局极小点，算法终止。

3.2. 数值实验

本节对 3个凸多目标规划问题进行数值实验，在

若干次迭代后都在最小弱有效解的某个邻域内终止，

表明所给的填充函数算法是有效的。算法中运用复形

调优法对原规划问题进行局部搜索，运用模式搜索法

对填充函数问题进行局部搜索，算法终止条件为







找第 k

。计算结果见各表，表中记号如下：是寻

个局部极小点的迭代步数；



是寻找第 1k



个

局部极小点时的参数值；







是寻找第 k个局部极

小点时的新的初始点；







是第 k个局部极小点；





,Fx



是第个新的初

k始点的函数值；





,Fx



是

极小点的函数

例3.1.

第k个局部值。













123

min, ,

x fxfxfx

.. 44,1,2

stxi









xxx



，





212

xxx其中，





xxxx。

先利用线性加权和法将其转化为单目标规划问题

(SP)：





 

1122123

m ,

Fxin

xfx f



 

 

.. 44,1,2

01,1

stxi





 



运用算法找到了原问题的最小弱有效解

，最小弱有效值，计算

结果见表1。

例 3.



*0,3 T

x



*2.9982fx 













min ,

.3, 1,2,3,4

fxfxfx

st xi



 

. 0

其中









 

11223

() max,,5fxgxg xf xgx





这里













010,1, 2,3

gxgxhxi





22 22

01234123

25521

xxxxxx xxx





22 22

112341234

28hxxxxxxxxx



 





2222

2123414

22hxxxxxxx10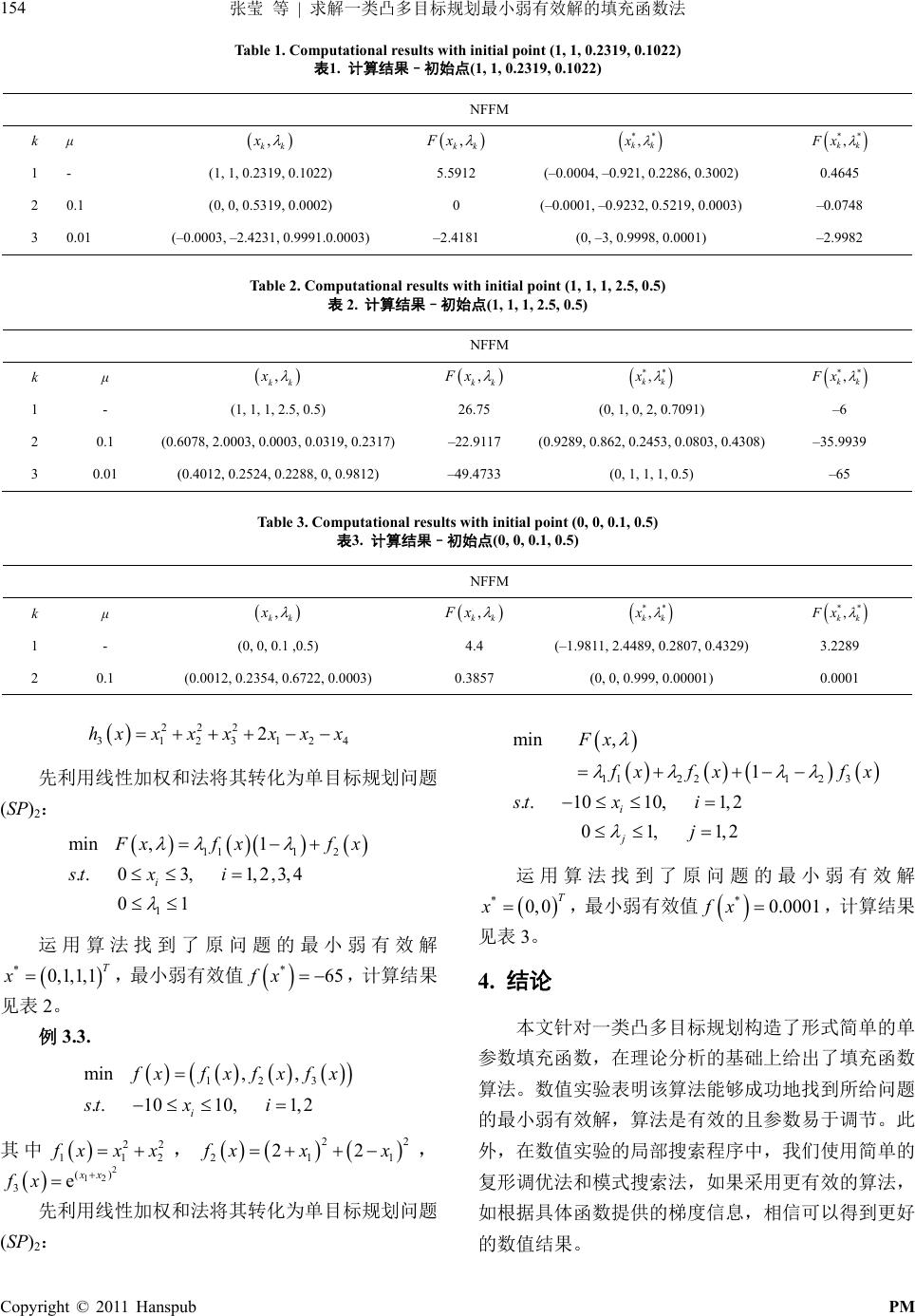





张莹等 | 求解一类凸多目标规划最小弱有效解的填充函数法

154

Table 1. Computanal results with initial point (1, 1, 0.2319, 0.1022)

表1. 初始点(1, 1, 0.2319, 0.1022)

tio

计算结果–

NFFM

k μ









Fx k













1 - (1, 1, 0.2319, 0.22) 5.5912 (–0.0004, –0.921, 0.286, 0.3002) 0.4645

(–0.0003) –2.

10 2

2 0.(0, 0, 0.5319, 0.0002) 0 (–0.0001, –0.9232, 0.5219, 0.0003) –0.0748

3 0.0103, –2.4231, 0.9991.0.004181 (0, –3, 0.9998, 0.0001) –2.9982

lts with Table 2. Computational resuinitial point (

表2. 计算结果–初始点(1, 1, 1, 2.5, 0.5)

1, 1, 1, 2.5, 0.5)

NFFM

k μ









Fx,













1 - (1, 1, 1, 2.5, 0.5) 26.75 (0, 1, 0, 2, 0.791) –6

(0.6078, 2.02317) – (0.9289, 0, 0.4308) –3

2 0.1 003, 0.0003, 0.0319, 0.22.9117 .862, 0.2453, 0.08035.9939

3 0.01 (0.4012, 0.2524, 0.2288, 0, 0.9812) –49.4733 (0, 1, 1, 1, 0.5) –65

ts with iniTable 3. Computational resultial point (0, 0,

表3. 计算结果–初始点(0, 0, 0.1, 0.5)

0.1, 0.5)

NFFM

k μ









,Fx













1 - (0, 0, 0.1 ,0) 4.4 (–1.9811, 2.4489, 0.2329) 3.2289

(0.0012, 03) 0

.5 807, 0.4

2 0.1 0.2354, 0.6722, 0.00.3857 (0, 0, 0.999, 0.00001) 0.0001

先利用线性加权和法将其转化为单目标规划问题

(SP)



312312

2hxxxxxxx





min ,

1010,1,2

01,1,2

 

112 2123

xfx fx

 

 

x i



  

 

2：







111 2

min ,1

.. 03,1,2,3,4

xfx f

st xi

 





 



运用算法找到了原问题的最小弱有效解

见表 2。





，最小弱有效值



，计算结果

例3.3.

*0,1,1,1 T

x*65fx 





123

in, ,

..1010,1,2

x fxfxfx

stxi



 

其中 2



xxx，1

 

xx x 

运用算法找到了原问题的最小弱有效解

，最小弱有效值，计算结果

见表 3。

4. 结

对一类凸多目标规划构造了形式简单的单

参数填充函数，在理论分析的基础上给出了填充函数

实验表明该算法能够成功地找到所给问题

的最

的数值结果。



*0, 0T

x



*0.0001fx

论

本文针

算法。数值

小弱有效解，算法是有效的且参数易于调节。此

外，在数值实验的局部搜索程序中，我们使用简单的

复形调优法和模式搜索法，如果采用更有效的算法，

如根据具体函数提供的梯度信息，相信可以得到更好

，

先利用线性加权和法将其转化为单目标规划问题

(SP)2：



fx 2

()

exx



张莹等求解一类凸多目标规划最小弱有效解的填充函数法155

[2] 仇秋生, 集值优化问题全局极小解集的连通性[J]. 浙江

大学学报(自然科学版), 2009, 32(3): 257-261.

ulti-objective linear progra

al programming approach.

r global optimization. Journal of Systems

参考文献 (References)

[1] D. S. Liu, K. C. Tan, and S. Y. Huang. On solving multiobjective

bin packing problems using evolutionary particle swarm optimi-

zation. European Journal of Operational Research, 2008, 190(2):

357-382.

师范

[3] I. A. Baky. Solving multi-level m

ming problems through fuzzy go

Ap-

Computation, 2009, 225(1): 68-79.

[9] W. X. Wang, Y. L. Shang, and L. S. Zhang. A filled function

method with one parameter for box constrained global optimiza-

plied Mathematical Modelling, 2010, 34(9): 2377-2387.

[4] 林锉云, 董加礼. 多目标优化的方法与理论[M]. 长春: 吉林

教育出版社, 1992.

[5] R. P. Ge. The theory of filled function methods for finding global

minimizres of nonlinearly constrained minimization problems.

Journal of Computational Mathematics, 1987, 5: 1-9.

[6] W. X. Zhu. A class of filled functions irrelevant to the number of

local minimizers fo

Science and Mathematical Sciences, 2002, 22(4): 406-413.

[7] M. Kong. On the filled function method for nonsmooth program.

Journal of Systems Science and Mathematical Sciences, 2004,

20(4): 149-154.

[8] C. J. Wang, Y. J. Yang, and J. Li. A new filled function method

for unconstrained global optimization. Applied Mathematics and

tion. Applied Mathematics and Computation, 2007, 194(1): 54-

66.