Pure Mathematics
Vol.06 No.03(2016), Article ID:17687,6
pages
10.12677/PM.2016.63039
Dependence of Eigenvalues of Sturm-Liouville Problem Whose Weight Function  on the Potential Function
on the Potential Function
Muyao Guo, Yunlan Gao*, Xin Zhao
College of Science, Inner Mongolia University of Technology, Hohhot Inner Mongolia

Received: May 8th, 2016; accepted: May 20th, 2016; published: May 27th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the eigenvalues of Sturm-Liouville problem whose weight function  dependent on the potential function are studied, and the comparison theorem and domain monotonicity are used.
dependent on the potential function are studied, and the comparison theorem and domain monotonicity are used.
Keywords:Sturm-Liouville Problem, Potential Function, Eigenvalues

权函数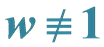 的Sturm-Liouville问题的特征值对势函数的依赖性
的Sturm-Liouville问题的特征值对势函数的依赖性
郭慕瑶,高云兰*,赵馨
内蒙古工业大学理学院,内蒙古 呼和浩特

收稿日期:2016年5月8日;录用日期:2016年5月20日;发布日期:2016年5月27日

摘 要
本文利用比较定理和定义区间的单调性证明了权函数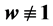 的Sturm-Liouville问题的特征值对势函数的依赖性。
的Sturm-Liouville问题的特征值对势函数的依赖性。
关键词 :Sturm-Liouville问题,势函数,特征值

1. 引言
经典的Sturm-Liouville (S-L)问题起源于19世纪初Fourier对热传导问题的数学解决方法。20世纪80年代以来曹之江,孙炯,刘景麟,尚在久,王万义等从不同角度对S-L问题进行了大量的研究。文献 [1] [2] Dauge和Helffer考虑的是二阶S-L方程

给出了Neumann特征值作为端点函数满足方程 ,以及Dirichlet特征值作为端点函数满足方程
,以及Dirichlet特征值作为端点函数满足方程 。证明了最小的Neumann特征值作为端点的函数是增加的,当区间长度趋向于零时极限存在。特别的,最小的Dirichlet特征值作为端点的函数是减小的,当区间长度趋向于零时,没有给出是否有极限。文献 [3] [4] 统一给出了特征值作为端点的函数满足的方程
。证明了最小的Neumann特征值作为端点的函数是增加的,当区间长度趋向于零时极限存在。特别的,最小的Dirichlet特征值作为端点的函数是减小的,当区间长度趋向于零时,没有给出是否有极限。文献 [3] [4] 统一给出了特征值作为端点的函数满足的方程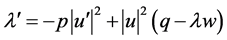 ,其中
,其中 是归一化的特征函数。证明了当区间长度趋近于零时,最小的Dirichlet特征值趋于无穷大。
是归一化的特征函数。证明了当区间长度趋近于零时,最小的Dirichlet特征值趋于无穷大。
本文的动机来源于文献 [5] [6] 的工作,他们研究了权函数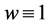 的S-L方程
的S-L方程

基于Dirichlet边界条件
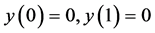 ,
,
证明了以上S-L问题的特征值对势函数的依赖性。我们考虑的权函数 的S-L问题:
的S-L问题:

其中实值函数 且
且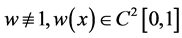 。
。
2. 主要结论
我们考虑以下权函数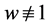 的S-L问题:
的S-L问题:
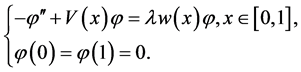 (1)
(1)
其中
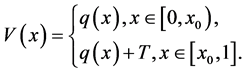
 是连续函数,
是连续函数,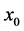 是
是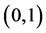 中任意固定一点。设
中任意固定一点。设 是问题(1)在
是问题(1)在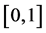 上的第m个特征值
上的第m个特征值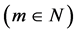 。可以看出
。可以看出 是
是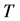 的函数。再设
的函数。再设 是定义在区间
是定义在区间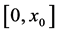 上S-L问题,即
上S-L问题,即
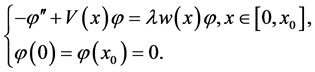 (2)
(2)
的特征值。设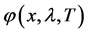 为方程
为方程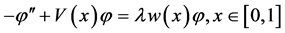 满足初始条件
满足初始条件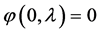 ,
,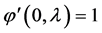 的解。当
的解。当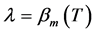 时,
时,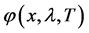 为上述S-L问题(1)的特征函数。这里
为上述S-L问题(1)的特征函数。这里 是归一化特征函数即满足
是归一化特征函数即满足 。
。
引理2.1 若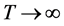 ,则对每一个整数
,则对每一个整数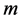 有
有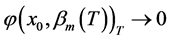 。
。
证明:令 。因
。因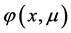 是满足上述S-L方程的解,由文献 [7] 和文献 [8] ,
是满足上述S-L方程的解,由文献 [7] 和文献 [8] ,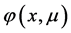 可表示为:
可表示为:

因此可以得到

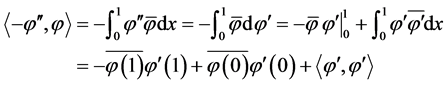
其中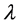 为实特征值,有
为实特征值,有 ,则
,则

于是上式可得

其中 。故
。故
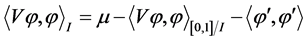 (3)
(3)
又因为
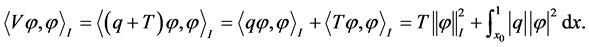 (4)
(4)
由(3)和(4)可知,
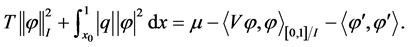 (5)
(5)
下面分 和
和 两种情形进行证明:
两种情形进行证明:
情形I 当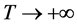 时,由
时,由 和(5)式知:
和(5)式知:
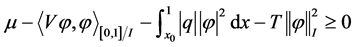 ,
,
变形得
 (6)
(6)
因为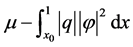 的有界性,所以存在正数
的有界性,所以存在正数 ,使得
,使得
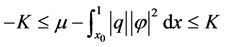 (7)
(7)
结合(6)和(7)式知:

即当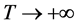 ,
,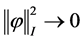 。
。
情形II ,由
,由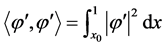 的有界性,所以有正数
的有界性,所以有正数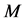 使得
使得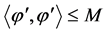 ,则
,则

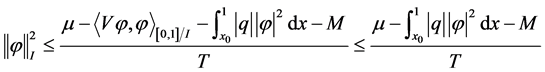 (8)
(8)
因为 的有界性,故存在正数
的有界性,故存在正数 ,有
,有

当 时有
时有
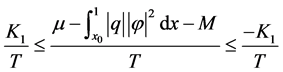 (9)
(9)
结合(8)和(9)式知:
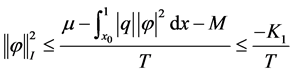
即当 时,
时,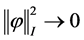 。
。
综合上述两种情形有: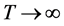 时,
时,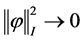 。由于
。由于 ,所以
,所以 。
。
可知 是区间
是区间 上每个点都收敛到0的连续函数,故
上每个点都收敛到0的连续函数,故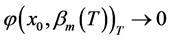 。
。
引理2.2 当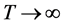 时,
时,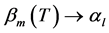 ,其中
,其中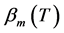 为问题(1)的特征值,
为问题(1)的特征值,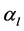 为问题(2)的特征值。
为问题(2)的特征值。
证明:分两种情形讨论:
情形I 当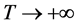 时,由比较定理得
时,由比较定理得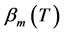 是
是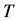 的单调递增函数。由定义区间单调性有:
的单调递增函数。由定义区间单调性有: ,因此当
,因此当 时,
时, 有极限。由引理2.1可得:
有极限。由引理2.1可得:
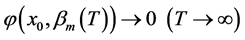
因为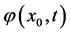 是
是 的连续函数,再由
的连续函数,再由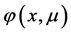 表达式可知:
表达式可知: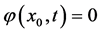 。则
。则 是区间
是区间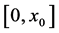 上的特征值,且
上的特征值,且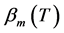 趋近于其中某一个特征值,即存在
趋近于其中某一个特征值,即存在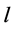 使得
使得 。
。
情形II 同理可得 。
。
引理2.3 当 时,
时, ;当
;当 时,
时,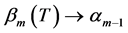 。
。
证明:由引理2.2的结论:当 时,
时,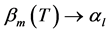 。下面证明
。下面证明 即可。运用数学归纳法,分两种情形证明:
即可。运用数学归纳法,分两种情形证明:
情形I 设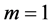 时,因为
时,因为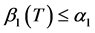 且
且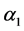 无零点,故有
无零点,故有 。又设
。又设 时有,有
时有,有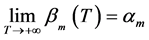 ,因为
,因为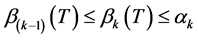 。
。
由 的表达式可知
的表达式可知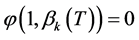 ,所以
,所以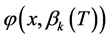 在
在 无零点。由定义区间的单调性和零点定理(可参考文献 [9] )知:
无零点。由定义区间的单调性和零点定理(可参考文献 [9] )知: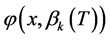 比
比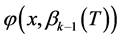 多一个零点。当
多一个零点。当 时,
时, 在
在 中所以零点都在
中所以零点都在 中。且当
中。且当 和
和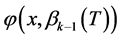 穿过
穿过 轴时,因为S-L问题的特征函数无重根,故
轴时,因为S-L问题的特征函数无重根,故 和
和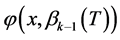 有相反的符号。由引理2.1可知
有相反的符号。由引理2.1可知 在每个零点处都与
在每个零点处都与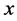 轴相交,所以
轴相交,所以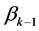 和
和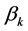 在
在 的某些特征值两侧。
的某些特征值两侧。
则当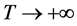 时,
时, 。根据单调有界原理得,
。根据单调有界原理得,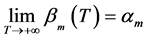 。
。
情形II 同理可得当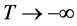 ,
, 。根据单调有界原理得
。根据单调有界原理得 。
。
下面叙述并证明本文的结果如下:
定理2.1 设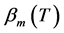 为问题(1)的特征值,
为问题(1)的特征值,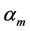 为问题(2)的特征值,则
为问题(2)的特征值,则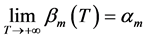 ;特别的,存在
;特别的,存在 ,使得
,使得 时有
时有 。
。
证明:考虑方程 ,若
,若 ,那么
,那么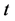 是
是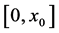 中的一个特征值。由文献 [7] 可知
中的一个特征值。由文献 [7] 可知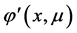 的方程为
的方程为
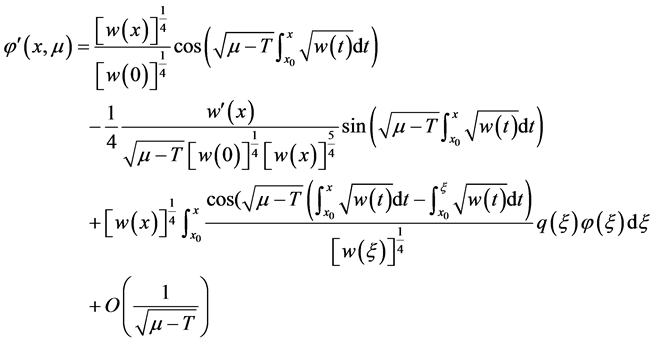
故由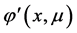 的方程可知,对
的方程可知,对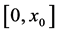 中的任意特征值
中的任意特征值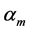 ,有
,有
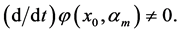
如果 ,由隐函数定理:存在唯一的函数
,由隐函数定理:存在唯一的函数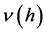 使得
使得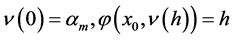 。所以
。所以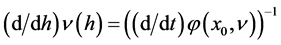 是有界的,存在正数
是有界的,存在正数 ,使得
,使得 。
。
由引理2.3可知,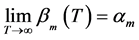 。因为
。因为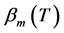 和
和 有相同的极限,且是方程
有相同的极限,且是方程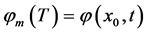 的解。所以当
的解。所以当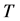 充分大时,有
充分大时,有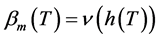 。
。
由引理2.1可知,当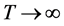 时,存在
时,存在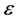 使得
使得 ,选取
,选取
 (对所有)
(对所有)
因为 。当
。当 ,有
,有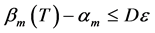 。所以
。所以 。
。
类似的可以得到定理2.2。
定理2.2 设 为问题(1)的特征值,
为问题(1)的特征值,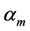 为问题(2)的特征值,则
为问题(2)的特征值,则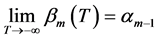 ;特别的,存在
;特别的,存在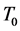 ,使得
,使得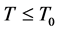 时有
时有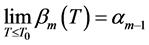 。
。
证明:按照定理2.1的证明可证得该定理。
文章引用
郭慕瑶,高云兰,赵 馨. 权函数w≢1的Sturm-Liouville问题的特征值对势函数的依赖性
Dependence of Eigenvalues of Sturm-Liouville Problem Whose Weight Function w≢1 on the Potential Function[J]. 理论数学, 2016, 06(03): 255-260. http://dx.doi.org/10.12677/PM.2016.63039
参考文献 (References)
- 1. Dauge, M. and Helffer, B. (1993) Eigenvalues Variation, I. Neumann Problem for Sturm-Liouville Operators. Diffe-rential Equations, 104, 243-262. http://dx.doi.org/10.1006/jdeq.1993.1071
- 2. Dauge, M. and Helffer, B. (1993) Eigenvalues Variation, II. Neumann Problem for Sturm-Liouville Operators. Differential Equations, 104, 263-297. http://dx.doi.org/10.1006/jdeq.1993.1072
- 3. Kong, Q, and Zettl, A. (1996) Dependence of Eigenvalues of Sturm-Liouville Problems on the Boundary. Differential Equations, 126, 389-407. http://dx.doi.org/10.1006/jdeq.1996.0056
- 4. Kong, Q. and Zettl, A. (1996) Eigenvalues of Regular Sturm-Liouville Problems. Differential Equations, 131, 1-19. http://dx.doi.org/10.1006/jdeq.1996.0154
- 5. Paul Phillips, D. (2005) A Partial Inverse Sturm-Liouville Problem: Matching a Step Function Potential to a Finite Eigenvalue List. Journal of Mathematical Analysis and Applications, 312, 248-260. http://dx.doi.org/10.1016/j.jmaa.2005.03.038
- 6. 张婷婷, 魏广生. Sturm-Liouville问题的特征值对势函数的依赖性[J]. 纯粹数学与应用数学, 2012, 28(2): 232- 237.
- 7. 王琳, 高云兰, 符权有. 权函数 时二阶右定Sturm-Liouville问题特征值的渐进式[J]. 内蒙古工业大学学报, 2013, 32(1): 1-5.
- 8. Evitan, B.M. (1949) On the Determination of a Sturm-Liouville Equation by Two Spectra. Nordisk Matematisk Tidskrift, B, 25-30.
- 9. Chavel, I. (1984) Eigenvalues in Riemannian Geometry. Academic Press, Orlando.
NOTES
*通讯作者。