Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21470,10
pages
10.12677/AAM.2017.64069
Numerical Inversion for the Fractional Order in the Variable-Order Space-Fractional Diffusion Equation
Di Liu, Shuxiang Wang
Guangzhou Maritime University, Guangzhou Guangdong

Received: Jul. 2nd, 2017; accepted: Jul. 21st, 2017; published: Jul. 25th, 2017

ABSTRACT
We consider a variable-order fractional advection-diffusion equation. Explicit approximations for the equation are proposed. Stability and convergence of the methods are discussed. Moreover, the homotopy regularization algorithm is applied to solve the inverse problem, and numerical examples are presented.
Keywords:Variable-Order Fractional Diffusion Equation, Inverse Problem, Homotopy Regularization Algorithm, Numerical Inversion
变空间分数阶扩散方程微分阶数的数值反演
刘迪,王淑香
广州航海学院基础教学部,广东 广州
收稿日期:2017年7月2日;录用日期:2017年7月21日;发布日期:2017年7月25日

摘 要
本文探讨一维变空间分数阶对流扩散方程,应用改进了的Grunwald-Letnikov分数阶导数定义对方程进行了离散,建立了隐式差分格式,并证明了该差分法的收敛性和稳定性。其次应用同伦正则化算法给出一维变空间分数阶扩散模型微分阶数的数值反演模拟,并讨论不同条件下的反演结果。
关键词 :变分数阶扩散方程,反问题,同伦正则化,数值反演

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在自然科学的很多领域都是由对流扩散方程和方程组来描述的,例如热传导、动力学、原子反应、生物形态、化学反应等等。传统的对流扩散方程是描述溶质在多孔介质中迁移扩散的经典模型。对于反常扩散,则是非马尔可夫(时间上)、非局域性(空间上)的运动,因此需要考虑运动过程的时空相关性,引入分数阶微积分,进而得到分数阶反常扩散模型 [1] [2] [3] [4] [5] 。传统的对流扩散方程其时间导数、空间导数分别为一阶和二阶的整数阶导数,分数阶扩散方程是由传统的扩散方程演变而来的,即时间导数的阶数由1变为(0,1)区间的一个数或者空间导数的阶数由2变为(1,2)区间的一个数。
近些年来越来越多的研究者发现:许多动力过程中的变量体现出分数阶的表现形态及可以随着时间和空间而变动,越来越多的事实表明变分数阶计算为描述复杂动力问题提供了有效的数学框架,例如Coimbra [6] , Copper与Crown [7] ,以及Tseng [8] 等分别从粘弹性力学、地理数据与信号处理研究等领域展示了变阶微分算子的应用。变分数阶模型及相应的变阶算子为描述复杂的动力问题提供了新的数学构架。
由于变阶算子中有一个变阶的指数部分,求解变分数阶微分方程的解析解难度更大,因此,很少有人研究变分数阶的解析解问题。数学上,鉴于适定性理论研究的困难性,目前对于变分数阶扩散方程的研究主要集中在数值求解方面,且主要是有限差分法.刘发旺教授及其团队对于变分数阶扩散模型的差分求解方法做出了一些开创性的工作 [9] [10] [11] [12] 。国内也有一些类似的研究工作,如马维元等 [13] ,马亮亮等 [14] 对不同类型的变阶扩散方程给出了有效的隐式差分格式。
本文探讨一维变空间分数阶对流扩散方程,应用改进了的Grunwald-Letnikov分数阶导数定义对方程进行了离散,建立了隐式差分格式,并证明了该差分法的收敛性和稳定性。进一步应用同伦正则化算法探讨了确定随着时间/空间变化的微分阶数的反问题。
2. 正问题及其数值求解
我们考虑非线性源项的变分数阶对流–扩散方程
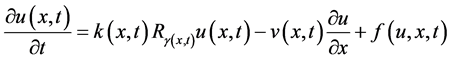
 (1)
(1)
初值条件和边界条件分别为
 (2)
(2)
 (3)
(3)
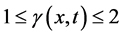 是空间分数阶导数的阶数,
是空间分数阶导数的阶数,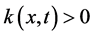 是扩散系数,
是扩散系数, 是平均对流速度。
是平均对流速度。 是源项并且满足Lipschitz条件
是源项并且满足Lipschitz条件
对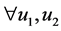 ,
, ,
,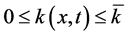 ,
,
在(1)中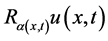 变阶分数导数定义为
变阶分数导数定义为
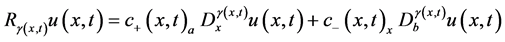
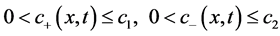
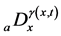 指Riemann-Liouville左侧分数导数,
指Riemann-Liouville左侧分数导数, 指Riemann-Liouville右侧分数导数。当
指Riemann-Liouville右侧分数导数。当 时,则为含有非线性源项的经典的对流扩散方程
时,则为含有非线性源项的经典的对流扩散方程
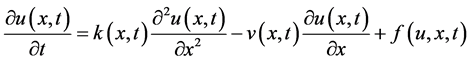
2.1. 差分格式
对(1)~(3)方程进行离散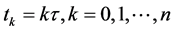 ,
,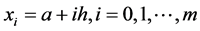 ,
, ,其中
,其中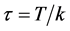 和
和 分别是时间和空间步长,
分别是时间和空间步长,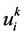 是
是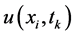 的数值近似,同样我们有
的数值近似,同样我们有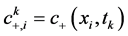 ,
,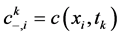 ,
,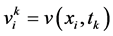 ,
, ,
,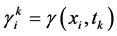 。
。
我们采用改进的Grunwald公式来离散空间分数阶导数,在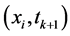 处分数阶导数离散为
处分数阶导数离散为
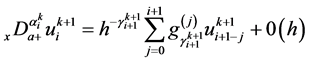
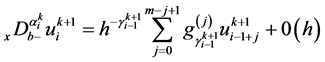 (4)
(4)
其中
 (5)
(5)
按照通常的差分离散方法,方程中的整数阶导数有如下近似:
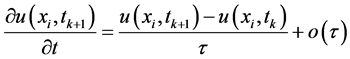
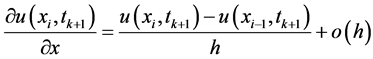
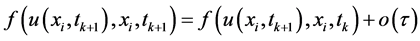 (6)
(6)
把(4)(6)代入方程我们得到如下隐式差分格式:
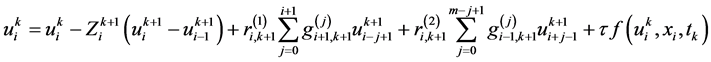
其中,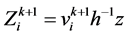 ,
, ,
,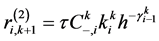 。边界初始条件为
。边界初始条件为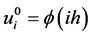 ,
,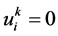 ,
, ,
, 以及
以及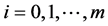 。
。
以矩阵形式表示的差分格式为
 (7)
(7)
其中
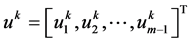 ,
,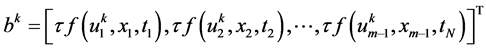
系数矩阵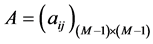 ,定义为
,定义为
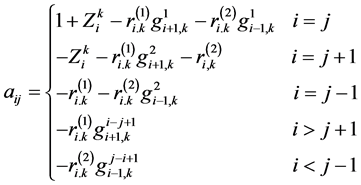 (8)
(8)
2.2. 稳定性和收敛性分析
为证明隐式差分方程格式的稳定性和收敛性,需要以下证明
引理1. 对于上述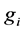 和
和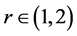 有
有
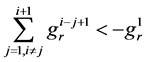
其中 ,
, ,
,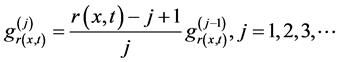 ,
,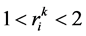 ,
,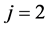 ,
,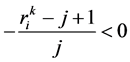 ,
, ,
, ,
,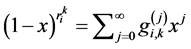 ,
,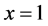 ,
, ,
,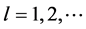 ,
,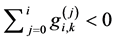 ,则
,则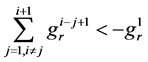 。
。
同理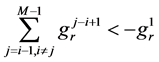 。注意到(8)给出矩阵A的结构,有如下命题:
。注意到(8)给出矩阵A的结构,有如下命题:
命题1. 矩阵A是严格对角占优的,即有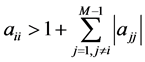
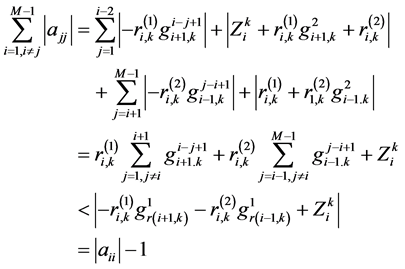
至此,命题1证明结束。
由命题1我们知道以A为系数矩阵的差分格式具有唯一解。进一步,我们证明它的稳定性。
定理1. 对于矩阵A,记 有
有
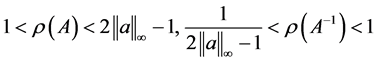 (9)
(9)
证明设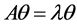 ,其中
,其中 为矩阵A的特征值。
为矩阵A的特征值。 为相应的特征向量,不失一般性,记
为相应的特征向量,不失一般性,记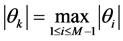 ,有
,有
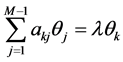
又
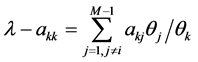
由命题1,注意到 得
得
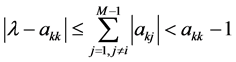
因此,
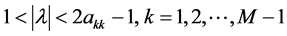
故(4.2.6)式成立。
引理2. 对于矩阵A及任意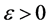 ,至少存在一种矩阵范数
,至少存在一种矩阵范数 使
使
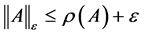
定理2. 隐式差分格式无条件稳定
证明利用引理2,对于系数矩阵的逆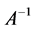 取
取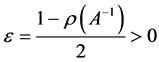 ,则存在某种范数
,则存在某种范数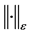 使得
使得
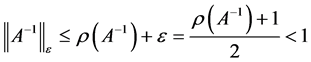
记初始扰动为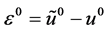 ,第k层的扰动为
,第k层的扰动为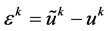 ,由(7)的线性知
,由(7)的线性知
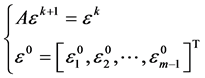
因而基于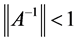 即有
即有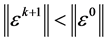 ,即差分格式是无条件稳定的。
,即差分格式是无条件稳定的。
进一步,我们讨论该格式的收敛性,记
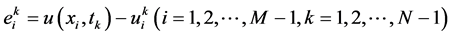
其中 表示真解在离散点
表示真解在离散点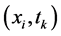 处的值,
处的值, 表示数值解在离散点
表示数值解在离散点 处的值。
处的值。 注意到
注意到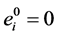 。同样由差分格式(7)是线性的,
。同样由差分格式(7)是线性的,
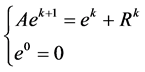
其中 表示解逼近过程中的阶段误差。可知存在常数
表示解逼近过程中的阶段误差。可知存在常数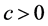 使
使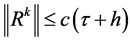 。由
。由 的性质,
的性质,
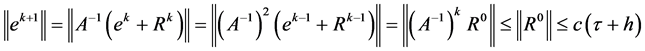
收敛性证明完毕。
2.3. 数值算例
考虑变分数阶对流扩散方程
 ,
,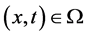
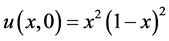 ,
,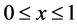 ,
, ,
,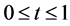
其中
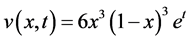
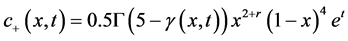
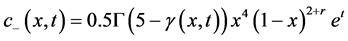
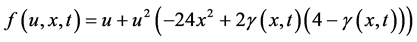
以上的真解为 ,微分阶数
,微分阶数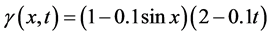 ,利用上一节的有限差分法进行数值计算,其中
,利用上一节的有限差分法进行数值计算,其中 表示
表示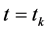 时的解误差,
时的解误差,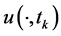 表示真解,
表示真解, 表示数值。
表示数值。
(1) 考察时间空间步长对正问题的影响,结果列于表1,表2,表3。
由表1可以看出,随着时间空间步长的减小,误差逐渐减小。
由表2可以看出,空间步长不变,误差随着时间步长的减小逐渐减小,当时间步长小于1/50时,随着时间步长的减小,解误差变化不大。
由表3可以看出,时间步长不变,随着空间步长的减小,误差逐渐减小
(2) 当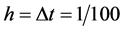 ,
,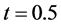 时方程解析解与数值解的比较,如图1。
时方程解析解与数值解的比较,如图1。
(3) 当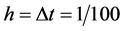 ,
, 时真实解与数值解得比较,如图2。
时真实解与数值解得比较,如图2。
Table 1. The impact of space tme step of the direct problem
表1. 空间时间步长对正问题的影响
Table 2. The effect of time step on error ()
表2.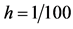 时间步长对误差的影响
时间步长对误差的影响
Table 3. The influence of space step size on error ()
表3.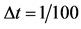 时空间步长对误差的影响
时空间步长对误差的影响
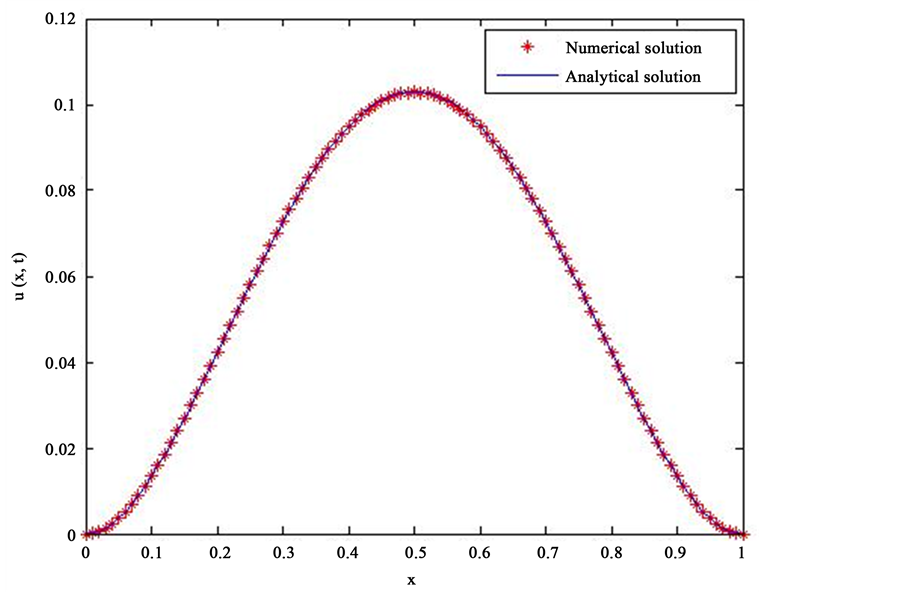
Figure 1. Comparison of real solution and numerical solution for t = 0.5
图1. t = 0.5时真实解与数值解得比较
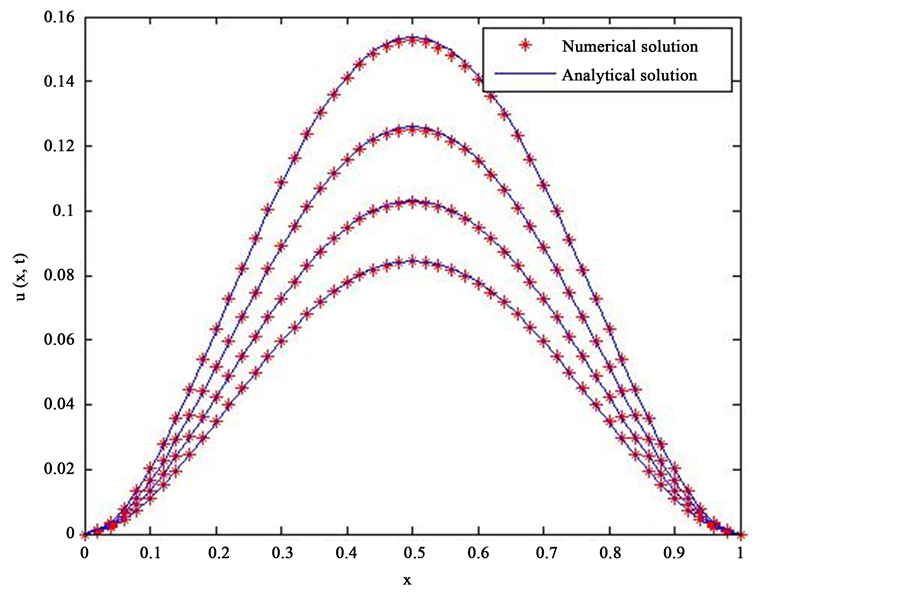
Figure 2. Comparison of real solution and numerical solution (t = 0.3, 0.5, 0.7, 0.9)
图2. t = 0.3,0.5,0.7,0.9时真实解与数值解得比较
3. 反问题及其数值反演
对于模型(1)~(3),实际问题中会有一些参数难以直接获得,这里需要增加适当的条件(附加观测数据),来确定和识别未知模型参数,这就是反问题。微分阶数是刻化分数阶扩散的首要标志,由于实际问题中微分阶数是未知的,很难通过实验手段直接测量,所以对于微分阶数反问题的研究具有重要意义。
这里我们选取终止时刻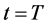 处的观测值作为附加数据,即有附加条件
处的观测值作为附加数据,即有附加条件
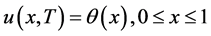 (10)
(10)
不过,实际应用中所获得的附加数据是在有限个点处测得得到的有限维数据,即实际的附加条件为
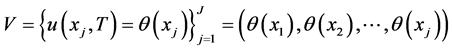 (11)
(11)
其中 为最终时刻,
为最终时刻,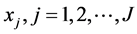 为观测点,称
为观测点,称 为附加数据向量,则由(1~3)联合附加条件(10)可构成一个确定微分阶数的反问题,应用的最佳摄动量算法,对微分阶数反问题进行数值模拟反演,详细步骤请参考 [15] [16] 。
为附加数据向量,则由(1~3)联合附加条件(10)可构成一个确定微分阶数的反问题,应用的最佳摄动量算法,对微分阶数反问题进行数值模拟反演,详细步骤请参考 [15] [16] 。
微分阶数为 ,
,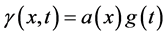 的形式。首先看数据取终值时刻
的形式。首先看数据取终值时刻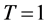 时在观测点处测得的数据,取收敛精度为eps=le-10.数值微分步长为
时在观测点处测得的数据,取收敛精度为eps=le-10.数值微分步长为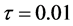 预估步数
预估步数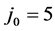 ,可调参数
,可调参数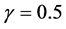 .接下来分别对分数阶的空间部分、时间部分分别进行数值反演。
.接下来分别对分数阶的空间部分、时间部分分别进行数值反演。
上述微分阶数固定 ,则对
,则对 进行反演,取多项式
进行反演,取多项式 作为逼近空间,根据
作为逼近空间,根据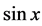 的泰勒展开式,真解
的泰勒展开式,真解 在
在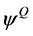 中近似表示为向量
中近似表示为向量
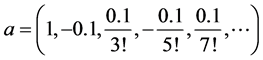
(1) 先取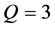 ,即
,即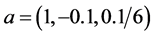 ,考察初始迭代对反演算法的影响.计算结果列于表4,其中
,考察初始迭代对反演算法的影响.计算结果列于表4,其中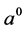 表示初始迭代值,
表示初始迭代值,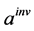 表示反演解,
表示反演解, 表示反演解与真解的误差,
表示反演解与真解的误差,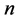 为迭代次数。
为迭代次数。
由表4可以看出,初始值选取对算法影响较大,且当其离真解较远时,迭代步数也相对较多.下面考察观测数据对反演算法的影响。
(2)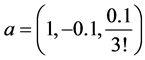 时,取初始值
时,取初始值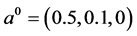 ,选取不同点的观测数据作为附加数据,考虑对反演算法的影响,如表5。
,选取不同点的观测数据作为附加数据,考虑对反演算法的影响,如表5。
(3) 当 在不同维数的逼近空间展开时,分别在维数为
在不同维数的逼近空间展开时,分别在维数为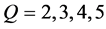 的逼近空间
的逼近空间
中反演,则相应的真解为
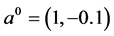 ,
, ,
,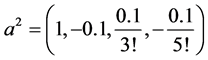 ,
,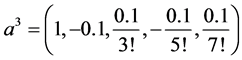
Table 4. The effect of initial iteration selection on inversion results
表4.初始迭代选取对反演结果的影响
这里初始迭代相应取为 ,
,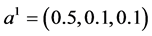 ,
,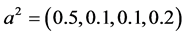 ,
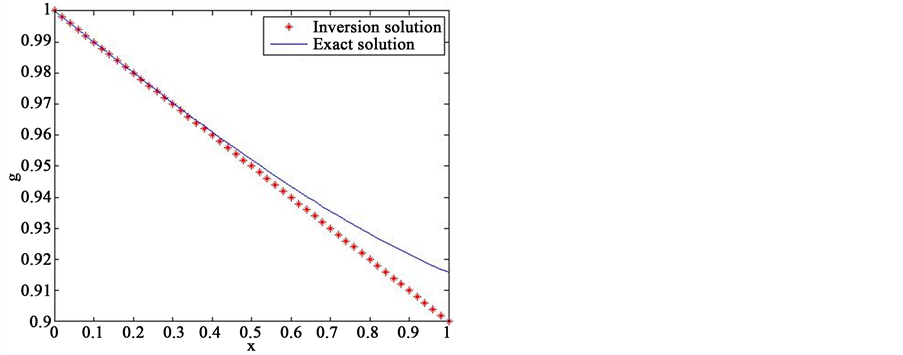
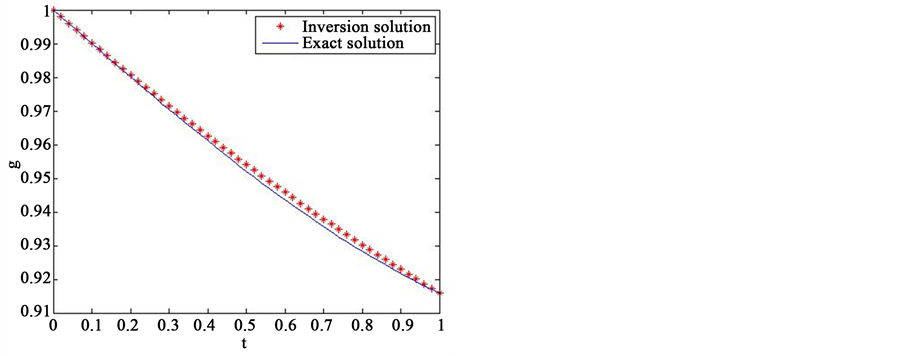
,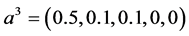 ,反演解与真解的图像分别绘于图3。
,反演解与真解的图像分别绘于图3。
由表5可以看出,取不同的内点作为附加数据,反演结果影响不大。
4. 结束语
本章主要考虑变空间分数阶一维对流扩散方程正问题的求解,应用改进了Grunwald-Letnikov的分数阶导数定义进行离散,建立了隐式差分格式,并分析该差分法的收敛性和稳定性。进一步对微分阶数进
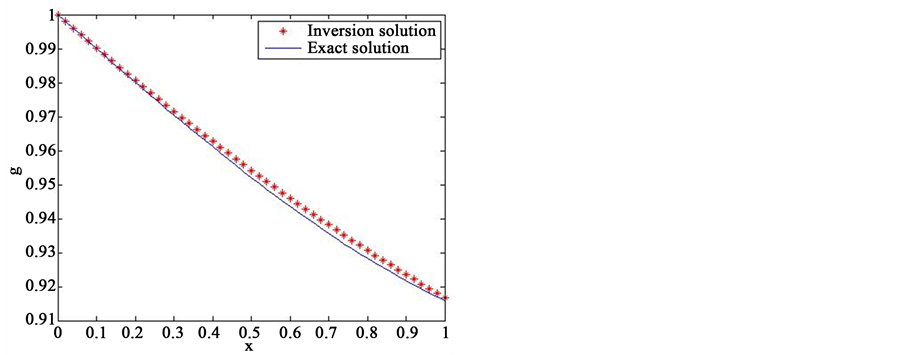

 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 3. Inverse solution and real solution of different approximation spaces. (a) Q = 2; (b) Q = 3; (c) Q = 3; (d) Q = 4
图3. 不同逼近空间中的反演解与真解。(a) Q = 2; (b) Q = 3; (c) Q = 3; (d) Q = 4
Table 5. The influence of the observation data of different points on the inversion results is selected
表5. 选取不同点的观测数据对反演结果的影响
行了数值反演模拟,并讨论了微分步长,初始迭代值,选取的空间维数等参数对反演的影响,结果表明,微分步长越小,初始迭代值越接近真解,选取的空间维数越多,反演效果越好。并且,对附加数据带扰动的情况进行了分析,随着扰动水平的减少,反演精度越高,证明了此算法的稳定性。
基金项目
广州航海学院人才引进项目E230202。
文章引用
刘迪,王淑香. 变空间分数阶扩散方程微分阶数的数值反演
Numerical Inversion for the Fractional Order in the Variable-Order Space-Fractional Diffusion Equation[J]. 应用数学进展, 2017, 06(04): 589-598. http://dx.doi.org/10.12677/AAM.2017.64069
参考文献 (References)
- 1. Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wiley, New York.
- 2. Podlubny, I. (1999) Fractional Differential Equations. Academic, San Diego.
- 3. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam.
- 4. 陈文, 孙洪广, 李西成, 等. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社, 2010.
- 5. 郭柏灵, 蒲学科, 黄凤辉. 分数阶偏微分方程及其数值解[M]. 北京: 科学出版社, 2011.
- 6. Coimbra, C.F.M. (2003) Mechanica with Variable-Order Differential Operators. Annalen der Physik, 12, 692-703.
- 7. Copper, G.R.J. and Rown, D.R.C. (2004) Filtering Using Variable Order Vertical Derivatives. Computers and Geosciences, 30, 455-459. https://doi.org/10.1016/j.cageo.2004.03.001
- 8. Tseng, C.C. (2006) Design of Variable and Adaptive Fractional Order FIR Differentiators. Signal Processing, 86, 2554-2566. https://doi.org/10.1016/j.sigpro.2006.02.004
- 9. Chen, C.M., Liu, F. and Anh, V. (2010) Numerical Schemes with High Spatial Accuracy for a Variable-Order Anomalous Subdiffusion Equation. SIAM Journal on Scientific Computing, 32, 1740-1760. https://doi.org/10.1137/090771715
- 10. Chen, C.M., Liu, F. and Anh, V. (2011) Turner I Numerical Simulation for the Variable-Order Galilei Invariant Advection Diffusion Equation with a Nonlinear Source Term. Applied Mathematics and Computation, 217, 5729-5742. https://doi.org/10.1016/j.amc.2010.12.049
- 11. Chen, C.M., Liu, F., Turner, I., Anh, V. and Chen, Y. (2013) Numerical Approximation for a Variable-Order Nonlinear Reaction-Subdiffusion Equation. Numerical Algorithms, 63, 265-290. https://doi.org/10.1007/s11075-012-9622-6
- 12. Zhuang, P., Liu, F., Anh, V. and Turner, I. (2009) Numerical Methods for the Variable-Order Fractional Advection-Diffusion Equation with a Nonlinear Source Term. SIAM Journal on Numerical Analysis, 47, 1760-1781.
- 13. 马维元, 张海东, 邵亚斌. 非线性变阶分数阶扩散方程的全隐差分格式[J]. 山东大学学报(自然科学版), 2013, 48(2): 93-97.
- 14. 马亮亮, 刘冬兵. Coimbra 变时间分数阶扩散方程–波动方程的新隐式差分法[J]. 西南师范大学学报(自然科学版), 2015, 40(3): 25-31.
- 15. 刘迪, 孙春龙, 李功胜, 贾现正. 变分数阶扩散方程微分阶数的数值反演[J]. 应用数学进展, 2015, 4(4): 326-335.
- 16. 贾现正, 张大利, 李功胜, 等. 等空间-时间分数阶变系数对流扩散方程微分阶数的数值反演[J]. 计算数学, 2014, 36(2): 113-132.
