Advances in Applied Mathematics
Vol.
09
No.
03
(
2020
), Article ID:
34780
,
8
pages
10.12677/AAM.2020.93052
Least Squares Method-Based Ellipse Model for Heart Sound Classification Research
Shuping Sun, Wei Song, Tingting Huang, Biqiang Zhang, Baojin Liu, Jie Wu, Hao Chen
Nanyang Institute of Technology, Nanyang Henan

Received: Mar. 4th, 2020; accepted: Mar. 20th, 2020; published: Mar. 27th, 2020

ABSTRACT
Heart sound classification is one of the important methods to diagnose heart disease, and its identification accuracy enables medical staff to provide more accurate treatment for patients. In view of this, in order to improve the recognition accuracy, this study proposes to generate classification boundary curve based on support vector machine (SVM). Considering the shape of classified boundary curve, a least square elliptical model based on classified boundary curve is established, which optimizes the complexity of heart disease diagnosis. Firstly, the classification boundary curve based on support vector machine is generated according to the frequency characteristics of the heart sound signal, and then the least square elliptical model based on the classification boundary curve is established to perform ellipse fitting on the classification boundary curve. To verify the effectiveness of elliptical model in heart sound recognition, an experimental analysis of online heart sound database and clinical heart sounds was carried out. 188 cases of atrial fibrillation, 181 cases of aortic regurgitation, 257 cases of mitral regurgitation, 325 cases of normal sound and 150 heart sounds of pulmonary stenosis were detected, and the classification accuracy was 91.7%, 98.8%, 99.8%, and 98.7%, proving that its classification has high precision.
Keywords:Heart Sound Signal, Support Vector Machines, Least Squares, Ellipse Mode

基于最小二乘法椭圆拟合在心音识别中的应用研究
孙树平,宋伟,黄婷婷,张弼强,刘保进,吴杰,陈 豪
南阳理工学院,河南 南阳

收稿日期:2020年3月4日;录用日期:2020年3月20日;发布日期:2020年3月27日

摘 要
心音识别是诊断心脏疾病的重要方法之一,其识别精度使医护人员为患者提供更加准确的治疗手段。鉴于此,为提高识别精度,本研究提出了基于支持向量机(SVM)对心音信号特征生成分类边界曲线,考虑到分类边界曲线的形状,建立了基于分类边界曲线的最小二乘法椭圆模型,优化了心脏疾病诊断的复杂性。其算法步骤为:首先根据心音信号的频率特征生成基于支持向量机的分类边界曲线,然后建立基于分类边界曲线的最小二乘法椭圆模型对分类边界曲线进行椭圆拟合。为验证在心音识别应用中椭圆模型的有效性,对在线心音数据库和临床心音的实验分析,即对188例房颤、181例主动脉瓣返流、257例二尖瓣返流、325例正常声音和150例肺动脉瓣狭窄心音进行检测,其分类精度分别为91.7%、98.8%。98.4%、99.8%和98.7%,证明其分类具有较高的精度。
关键词 :心音信号,支持向量机,最小二乘法,椭圆模型

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来心血管疾病的患病率和死亡率均呈现持续增长的趋势,并且心血管疾病死亡人数连续多年位居疾病死亡之首。据《中国心血管报告2018》 [1] 显示,2018年农村和城市因心血管疾病死亡人数占全部因疾病死亡人数的比例分别是46% (见图1(A))和43% (见图1(B))。同时报告指出我国目前大约有2.9亿患者,因此我国心血管病防治工作面临严峻挑战 [2]。目前诊断心血管病的方法包括无创式(心电图、胸透X射线、心音听诊、超声成像和多普勒技术)和有创式(血管造影术等) [3]。由于心音听诊具有非创伤性、价格低廉、操作简单等优点,因此利用心音诊断心血管病得到广泛的研究 [4]。而心音诊断的关键即诊断精度。

Figure 1. The main cause of death in rural and urban residents in China in 2018
图1. 2018年中国农村和城市居民主要疾病死因构成
关于心音诊断,国内外诸多学者广泛采用支持向量机技术对心音信号进行诊断识别 [5] [6] [7],然而采用支持向量机生成的分类函数过度依赖于数据点的个数,也就是说,随着学习样本数据量增加,将导致测试样本计算量增大,进而不利于大数据检测。鉴于此,本研究提出一种基于最小二乘法为支持向量机所获取的分类函数建立数学模型进而化简其复杂程度实现对心音信号识别。本研究主要内容包括心音特征提取、基于最小二乘法建立支持向量机椭圆模型、实验分析和结论,其总体结构组织如图2所示。

Figure 2. Overall structure flow chart
图2. 总体结构组织流程图
2. 心音特征提取
2.1. 心音信号的采集与预处理
本研究采用3M-3200电子听诊器 [8] 对心音数据进行采集:根据心音信号的频带范围,采样频率FS设置为44.1 kHz;基于所分析心血管病病理信息有效成分,主动脉瓣区设置为听诊区对心音信号进行采集。电子听诊器采集到的原始心音信号波形如图3(A)所示,其近似为周期信号,每个周期包含两个成分第一心音(S1)和第二心音(S2),同时不可避免包含大量背景噪声。根据心音预处理研究 [9] 所描述,基于小波变换采用dB10作为母小波可为心音信号预处理提供一种有效的途径,对心音信号进行降噪处理,保存21.5 Hz和689 Hz之间的频率成分,其降噪效果如图3所示,其中图3(A)为滤波之前的原始波形图,图3(B)为滤波后降噪效果图。对比图3(A),从图3(B)中可以明显观察到S1和S2的有效信息,而S1和S2之间的噪声得到有效的处理。
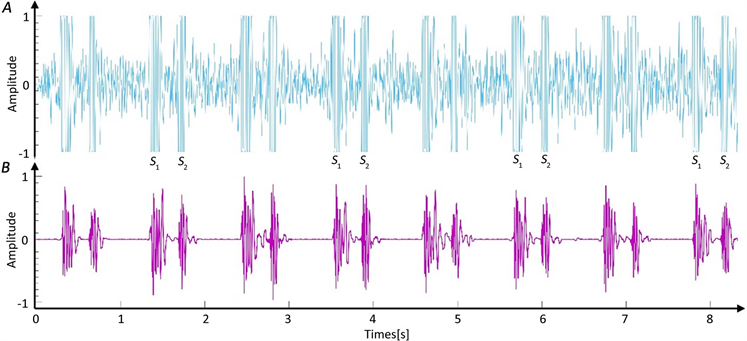
Figure 3. Comparison of heart sound signal before and after processing
图3. 心音信号处理前后对比
2.2. 心音信号的特征提取
由研究 [9] 知,利用S1与S2时间域距离结合频率域宽度作为特征能够有效区分正常和室间隔缺损心音信号,其定义方法如公式(1)~(5),特征提取结果如图4所示,(A)为时间域特征 定义方法,(B)为从 中提取的频域特征 ,其计算方法如公式(2)所示。图中ET指从心音ST中提取的包络线, 和 是第一心音和第二心音的重心, 和 是包络与阈值( )为0.2时的左右交叉点。

Figure 4. Heart sound signal feature map
图4. 心音信号特征图
(1)
(2)
其中
(3)
(4)
(5)
其中,N为心音周期长度,
和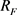 是包络与阈值(
是包络与阈值(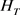 )为0.2时的左右交叉点。
)为0.2时的左右交叉点。
为消除特征之间相关性与减小特征维度,本研究采用主成分分析提取前两个主成分作为其心音特征以取代复杂的信息量,其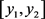 的散点图如图5所示,。
的散点图如图5所示,。
3. 基于最小二乘法建立支持向量机椭圆模型
3.1. 支持向量机
支持向量机(SVM)是由Vladimir Naumovich Vapnik开发的一种功能强大、应用广泛的机器学习技术 [10],其已成功应用于心音信号分析中 [11]。实际上,SVM就是最大限度找到样本数据最优分离超平面(线),关于SVM典型例证如图6所示,其中红线表示由SVM得到的最优函数分类曲线,+与*表示两类不同样本数据,圈中点即数据的支持向量。
3.2. 分类边界曲线的生成
分类边界曲线生成的主要步骤如下:首先由心音信号生成特征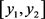 的散点图,然后根据高斯函数
的散点图,然后根据高斯函数
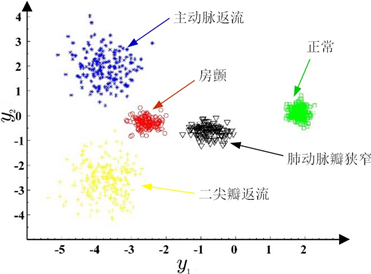
Figure 5. Feature [y1,y2] scatter diagram
图5. 特征[y1,y2]散点图

Figure 6. Optimal separation hyperplane
图6. 最优分离超平面
作为SVM技术的核函数,最后利用高斯核函数对输入向量x进行边界曲线分类。基于高斯核函数将输入向量x的分类边界曲线分为两类:正类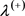 和负类
和负类 。表示为
。表示为
 (6)
(6)
其中
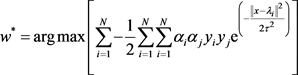 (7)
(7)
 (8)
(8)
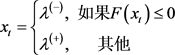 (9)
(9)
因此,对于检测样本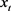 ,基于所生成的分类边界曲线的分类结果可以通过方程(6)~(9)确定。根据支持向量机边界曲线生成SVM分类边界曲线如图7(A)所示。虽然SVM技术的分类边界曲线具有较高精确度,但根据公式(6)可知,由于分类边界曲线数学表达式过于复杂,而且计算量大,为了克服这一问题,本研究提出了基于最小二乘法建立支持向量法椭圆模型。
,基于所生成的分类边界曲线的分类结果可以通过方程(6)~(9)确定。根据支持向量机边界曲线生成SVM分类边界曲线如图7(A)所示。虽然SVM技术的分类边界曲线具有较高精确度,但根据公式(6)可知,由于分类边界曲线数学表达式过于复杂,而且计算量大,为了克服这一问题,本研究提出了基于最小二乘法建立支持向量法椭圆模型。

Figure 7. SVM classification boundary curve
图7. SVM分类边界曲线
3.3. 基于最小二乘法的椭圆模型算法
为了简化分类边界曲线并使其参数化,考虑到边界曲线的椭圆模型(EMs),所以本研究提出了一种基于最小二乘法的椭圆模型。
椭圆一般方程为
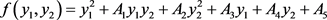 (10)
(10)
用矩阵方法表示为
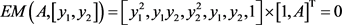 (11)
(11)
具有特定椭圆约束
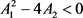 (12)
(12)
其中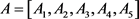 是椭圆EM的系数,
是椭圆EM的系数, 是椭圆EM上一点坐标。通过公式(13)计算Α
是椭圆EM上一点坐标。通过公式(13)计算Α
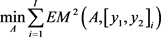 (13)
(13)
其中 为分类边界曲线F上的点。为了解决多变量约束非线性问题的最小化问题,利用MATLAB优化函数fmincon进行拟合,对优化问题进行求解,并将求解器设置为内点算法。根据以上公式(10)~(12)获得识别心血管疾病心音信号的椭圆模型,其对应于图7(B)中绘制的分类边界曲线。基于最小二乘法获得对应于图7(B)的椭圆模型优化结果绘制于表1中,其中
为分类边界曲线F上的点。为了解决多变量约束非线性问题的最小化问题,利用MATLAB优化函数fmincon进行拟合,对优化问题进行求解,并将求解器设置为内点算法。根据以上公式(10)~(12)获得识别心血管疾病心音信号的椭圆模型,其对应于图7(B)中绘制的分类边界曲线。基于最小二乘法获得对应于图7(B)的椭圆模型优化结果绘制于表1中,其中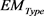 表示每种心音信号的椭圆模型。
表示每种心音信号的椭圆模型。
Table 1. Ellipse model optimization results
表1. 椭圆模型优化结果
4. 实验分析
通过对在线心音数据库和临床心音的实验分析,对188例房颤、181例主动脉瓣返流、257例二尖瓣返流、325例正常声音和150例肺动脉瓣狭窄心音进行分类检测,通过方程(14)来求出检测结果分类准确率,其中TP表示真正类,表示FP假正类,表示FN假负类,TN真负类。本研究与其他研究中提出的支持向量机方法、基于主成分分析离散隐含马尔可夫模型(PCA-DHMM)方法 [12] 和多级基础选择(MLBS)方法 [13] 进行了比较,结果如表2,相比其他学者提出的方法准确率有明显提高。
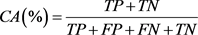 (14)
(14)
Table 2. Classification accuracy comparison
表2. 分类准确率比较
5. 结论
本研究通过最小二乘法的椭圆拟合算法为支持向量机所获取的分类函数建立椭圆模型。为验证该系统的可行性,本研究对188例房颤、181例主动脉瓣返流、257例二尖瓣返流、325例正常声音和150例肺动脉瓣狭窄心音进行检测,与之前学者提出的基于SVM的分类边界曲线方法、离散隐含马尔可夫模型和多级基础选择方法进行了比较。结果表明相比其他学者提出的方法,本研究提出的椭圆模型在心音诊断时具有计算简单、诊断准确率更高的优点。因此利用电子听诊器或移动设备进行计算机辅助听诊,并结合基于最小二乘法的椭圆拟合算法,可以作为一种智能的、经济的、能够自动检测心血管疾病的诊断方法。
文章引用
孙树平,宋 伟,黄婷婷,张弼强,刘保进,吴 杰,陈 豪. 基于最小二乘法椭圆拟合在心音识别中的应用研究
Least Squares Method-Based Ellipse Model for Heart Sound Classification Research[J]. 应用数学进展, 2020, 09(03): 429-436. https://doi.org/10.12677/AAM.2020.93052
参考文献
- 1. 胡盛寿, 高润霖, 刘力生, 等. 《中国心血管病报告2018》概要[J]. 中国循环杂志, 2019, 34(3): 209-220.
- 2. 许莉莉, 等. 基于最小二乘支持向量机的心音分类识别研究[J]. 中国医疗设备, 2017, 32(4): 38-41.
- 3. Sun, S. (2015) An Innovative Intelligent System Based on Automatic Diagnostic Feature Extraction for Diagnosing Heart Diseases. Knowledge-Based Systems, Elsevier, 75, 224-238. https://doi.org/10.1016/j.knosys.2014.12.001
- 4. Amiri, A.M. and Armano, G. (2013) Heart Sound Analysis for Diagnosis of Heart Diseases in Newborns. APCBEE Procedia, 7, 109-116. https://doi.org/10.1016/j.apcbee.2013.08.020
- 5. Sengur, A. (2012) Support Vector Machine Ensembles for In-telligent Diagnosis of Valvular Heart Disease. Journal of Medical Systems, 36, 2649-2655. https://doi.org/10.1007/s10916-011-9740-z
- 6. Lubaib, P. and Muneer, K.V.A. (2016) The Heart Defect Analysis Based on PCG Signals Using Pattern Recognition Techniques. Procedia Technology, 24, 1024-1031. https://doi.org/10.1016/j.protcy.2016.05.225
- 7. Li, J., Ke, L. and Du, Q. (2019) Classification of Heart Sounds Based on the Wavelet Fractal and Twin Support Vector Machine. Entropy, 21, 472. https://doi.org/10.3390/e21050472
- 8. https://www.littmann.com
- 9. Sun, S., Wang, H., Chang, Z., et al. (2019) On the Mahalanobis Distance Classification Criterion for a Ventricular Septal Defect Diagnosis System. IEEE Sensors Journal, 19, 2665-2674. https://doi.org/10.1109/JSEN.2018.2882582
- 10. 林香亮, 袁瑞, 孙玉秋, 王超, 陈长胜. 支持向量机的基本理论和研究进展[J]. 长江大学学报(自科版), 2018, 15(17): 48-53.
- 11. Sun, S., Wang, H. and Jiang, Z. (2014) Segmentation-Based Heart Sound Feature Extraction Combined with Classifier Models for a VSD Diagnosis System. Expert Systems with Applications, 41, 1769-1780. https://doi.org/10.1016/j.eswa.2013.08.076
- 12. Sarac, R. (2012) Hidden Markov Model-Based Classification of Heart Valve Disease with PCA for Dimension Reduction. Engineering Applications of Artificial Intelligence, 25, 1523-1528. https://doi.org/10.1016/j.engappai.2012.07.005
- 13. Safara, F., Doraisamy, S. and Azman, A. (2013) Multi-Level Basis Selection of Wavelet Packet Decomposition Tree for Heart Sound Classification. Computers in Biology and Medicine, 43, 1407-1414. https://doi.org/10.1016/j.compbiomed.2013.06.016
