Pure Mathematics
Vol.
12
No.
01
(
2022
), Article ID:
48363
,
9
pages
10.12677/PM.2022.121022
Morita环上的Gorenstein内射模
秦军霞
西北师范大学数学与统计学院,甘肃 兰州
收稿日期:2021年12月16日;录用日期:2022年1月19日;发布日期:2022年1月26日

摘要
设
是Morita环,其中
和
是环,
是
-双模,
是
-双模,并且
是Artin代数。本文主要研究了Morita环
上的Gorenstein内射模与代数A和代数B的关系。给出了函子
和函子
保持Gorenstein内射模的等价条件。设
是Morita环
上的一个Gorenstein内射模,本文也证明了在一定条件下
和
也是Gorenstein内射模。
关键词
Morita环,Gorenstein内射模,Artin代数,Gorenstein代数

Gorenstein-Injective Modules over Morita Rings
Junxia Qin
College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu
Received: Dec. 16th, 2021; accepted: Jan. 19th, 2022; published: Jan. 26th, 2022

ABSTRACT
Let
be a Morita ring, where A and B are rings, N is
-bimodule, M is
-bimodule, and
is an Artin algebra. In this paper we investigate the relations between the Gorenstein injective modules over a Morita ring
and algebras A and B. The equivalent conditions for functors
and
to preserve Gorenstein injective modules are given. Let
be a Gorenstein injective module on Morita ring
. It is also proved that
and
are Gorenstein injective modules under certain conditions.
Keywords:Morita Ring, Gorenstein Injective Modules, Artin Algebras, Gorenstein Algebras

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
H. Bass在其著作中介绍了Morita环的概念,这种环包含很多的代数例子。1969年,Auslander等人在文献 [1] 中引入了双边Noether环上的Gorenstein维数为零的模。2000年,Jenda等人在文献 [2] 中对于一个任意环R,研究了Gorenstein投射(内射、平坦)模及其维数。随后很多作者对Gorenstein投射(内射、平坦)模做了进一步的探索和推广,证明了它们的很多性质与投射(内射、平坦)模的性质类似。
本文讨论了Morita环上Gorenstein内射模与代数A和代数B之间的关系,定理3.2和定理3.6介绍了函子
和函子
保持Gorenstein内射模的等价条件。对于一个Morita环上的Gorenstein内射模
,定理3.7给出了使
和
成为Gorenstein内射左A-模和左B-模的条件。
2. 预备知识
本文中,环是具有单位元的结合环,模均是有限生成模。
设A是一个Artin代数,记
为有限生成左A-模范畴。用
表示内射(投射)左A-模,用
表示Gorenstein内射(投射)左A-模,用
表示M的投射(内射)维数。
设A,B是环,
是
-双模,
是
-双模,模同态
,模同态
。记
,设
, 中的加法按分量计算,乘法为
为了使
作成一个结合环,规定
,,,,则
关于普通矩阵的加法和上述定义的乘法作成一个环,文献 [3] 中称之为Morita环。
在文献 [3] 和文献 [4] 中已经对
环上的模进行了刻画。为了叙述方便,引入范畴
,它中的对象是四元组
,其中
,,, 并且满足如下交换图
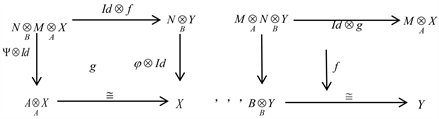
态射
和态射
的合成记为
,态射 和态射
的合成记为
。
和态射
的合成记为
。
设函子
,对于任意的
,,其中是
是一个Abel群,对
,,,,,, -模的结构如下
.
设
为
中的任意一个态射,定义
,
由文献 [4] 可知
与
等价,因此可用
中的对象
代替
-模。由文献 [5] 得一个Morita环
可以作为Artin代数的等价条件是存在交换环R,并且是Artin环,使得代数A与代数B均是Artin R-代数,M和N是有限生成R-模,并且R在M和N上都起中心作用。
设Morita环
,则根据文献 [6] 有:
1) 范畴
中的序列
正合
范畴
中的序列
正合且范畴
中的序列
正合。
2) 设
是范畴
中的一个态射,同态
,同态
,则有
,h和j由以下交换图诱导得出
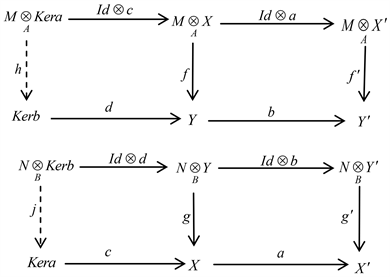
3) 设
是范畴
中的一个态射,同态
,同态
,则有
, 和
由以下交换图诱导得出
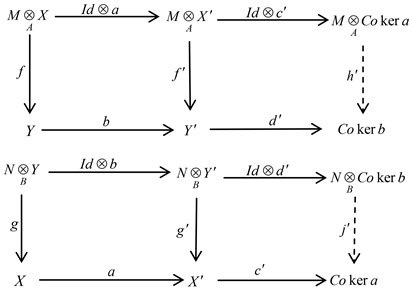
根据文献 [5],考虑如下几个函子:
对任意
和A-同态
,函子
定义为
,.
对任意
和B-同态
,函子
定义为
,.
对任意
和
-态射
,函子
定义为
,。
对任意
和
-态射
,函子
定义为
,。
对于每个
,记
为由involution给出的A-同态,构造B-同态
,它将
作用到
中,对任意
和A-同态
,函子
定义为
,.
对于每个
,记
为由involution给出的B-同态,构造A-同态
,它将
作用到
中,对任意
和B-同态
,函子
定义为
,.
下面命题是对以上几个函子的进一步刻画。
命题2.1 [5] 设Morita环
,并且
是Artin代数,则
1) 函子
,, 和
都是满忠实的;
2) 对子
,,, 均为函子的伴随对;
3) 函子
和
均为正合函子。
下面命题刻画了不可分解投射
-模和不可分解内射
-模。
命题2.2 [5] 设Morita环
,并且
是Artin代数,则
1) 不可分解投射
-模恰是
,
或
,
对
,且P不可分解,
,且Q不可分解。
2) 不可分解内射
-模恰是
,
或
,
对
且I不可分解,
且J不可分解。
定理2.3 [7] 设Morita环
是一个Gorenstein代数。
1) 若
, 的投射维数有限,则A是Gorenstein代数;
2) 若
, 的投射维数有限,则B是Gorenstein代数。
3. 主要结果
引理3.1 设A是一个Artin代数,
是一个
-双模,并且
, 是内射左A-模的正合复形,则
正合。
证明 设
的一个投射分解为
。因为每个
是左A-内射的,所以有正合复形
。又由于
,所以对
,有
正合,因此
正合。
定理3.2 设
是Gorenstein代数。
1) 设
。若
,则
;
2) 设
。若
,则
。
证明 1) 因为
,所以存在
的完全内射分解
,使得
。又因为
,所以由引理3.1知
正合。因此有内射
-模的正合列
,使得
.
又因为
是Gorenstein代数,所以对任意的内射
-模
,它的投射维数有限。因此可由引理3.1知
正合,即
是一个完全内射分解,故
。
2) 与1)的证明类似。
注记3.2 [7] Artin代数A是一个Gorenstein代数
对
,有
,并且对
,有
。
定义3.3 [8] 称一个内射左R-模的正合复形
是完全正合的,如果对
, 正合。
命题3.4 设Morita环
,并且
是Artin代数。
1) 设函子
将内射左A-模的正合复形作用成左B-模的正合复形,并且
是投射的,则复形
完全正合当且仅当复形
完全正合。
2) 设函子
将内射左B-模的正合复形作用成左A-模的正合复形,并且
是投射的,则复形
完全正合当且仅当复形
完全正合。
证明 1)
)设完全正合复形
,,,则有
正合。因此
正合。又因为
是伴随对,并且
正合,所以
保持内射对象,从而每个
。下证对任意
, 正合。事实上,根据命题2.2(2),只需证明复形
和复形
正合,其中
,。又因为
完全正合,所以对任意
,复形
正合,而由命题2.1知函子
是满忠实的,所以复形
正合。设
,由
是伴随对可得
,而
,因此有交换图
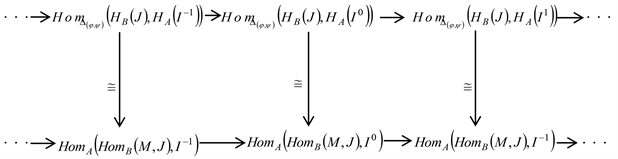
因为
是内射左A-模,所以复形
正合,因此复形
正合,从而
完全正合。
) 设
是左A-模的复形,使得
完全正合。用函子
作用
可得正合复形
由
是伴随对可得
左正合,并且
满忠实,因此每个
。因为
完全正合,
满忠实,所以对任意内射左A-模I,
正合。
2)与1)的证明对偶。
由命题3.4可得以下推论。
推论3.5 设Morita环
,并且
是Artin代数。
1) 设函子
将内射左A-模的正合复形作用成左B-模的正合复形,并且
是投射的。若
,则
;
2) 设函子
将内射左B-模的正合复形作用成左A-模的正合复形,并且
是投射的。若
,则
。
命题3.6 设Morita环
,并且
是Artin代数。
1) 设
, 是投射的。若
,则
;
2) 设
, 是投射的。若
,则
.
证明 1) 设
正合,其中
,。由题设知
,所以由引理3.1可得
正合。又因为
是投射的,
,所以可由推论3.5得
.
2) 与1)的证明类似。
定理3.7 设Morita环
,并且
是Artin代数,
是Gorenstein内射
-模。
1) 若
是自由的,A是Gorenstein代数,则
;
2) 若
是自由的,B是Gorenstein代数,则
。
证明 1) 设
,由命题2.2知存在完全内射分解

用函子
作用后得
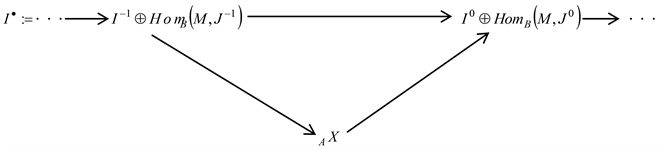
因为
是自由的,并且
,所以
,因此
。由于A是Gorenstein代数,故任意内射左A-模I有有限投射维数,由引理3.1知
正合,从而
是完全内射分解,因此
。
2)与1)的证明类似。
推论3.8 设Morita环
,并且
是Artin代数。
1) 设
是投射的,
,并且A是Gorenstein代数。设
是一个左A-模,则
当且仅当
;
2) 设
是投射的,
< ∞,并且
是Gorenstein代数。设
是一个左B-模,则
当且仅当
。
证明 由定理3.7和定理3.6可得。
推论3.9 设
是一个Gorenstein代数。
1) 设
是投射的,
。设
是一个左A-模,则
当且仅当
;
2) 设
是投射的,
。设
是一个左B-模,则
当且仅当
。
证明 由定理2.4,定理3.7和定理3.2可得。
本文主要研究了Morita环
上的Gorenstein内射模与代数A和代数B的关系,给出了函子
和函子
保持Gorenstein内射模的等价条件。
文章引用
秦军霞. Morita环上的Gorenstein内射模
Gorenstein-Injective Modules over Morita Rings[J]. 理论数学, 2022, 12(01): 174-182. https://doi.org/10.12677/PM.2022.121022
参考文献
- 1. Auslander, M. and Bridger, M. (1969) Stable Module Theory. Memoirs of the American Mathematical Society, Provi-dence, RI. https://doi.org/10.1090/memo/0094
- 2. Enochs, E.E. and Jenda, O.M.G. (2000) Relative Homological Algebra. Walter de Gruyter, Berlin.
https://doi.org/10.1515/9783110803662
- 3. Bass, H. (1968) Algebraic K-Theory. W A Benjamin, Inc., New York.
- 4. Green, E. (1982) On the Representation Theory of Rings in Matrix Form. Pacific Journal of Mathematics, 100, 123-138. https://doi.org/10.2140/pjm.1982.100.123
- 5. Green, E. and Psaroudakis, C. (2014) On Artin Al-gebras Arising from Morita Contexts. Algebras and Represent Theory, 17, 1485-1525. https://doi.org/10.1007/s10468-013-9457-4
- 6. Gao, N. and Psaroudakis, C. (2017) Gorenstein Homological Aspects of Monomorphism Categories via Morita Rings. Algebras and Representation Theory, 20, 487-529. https://doi.org/10.1007/s10468-016-9652-1
- 7. Asefa, D. (2021) Gorenstein-Projective Modules over Morita Rings. Algebra Colloquium, 28, 521-532.
https://doi.org/10.1142/S1005386721000407
- 8. Sergio, E., Fu, X.H. and Alina, I. (2017) Totally Acyclic Com-plexes. Journal of Algebra, 470, 300-319.
https://doi.org/10.1016/j.jalgebra.2016.09.009







 和态射
的合成记为
。
和态射
的合成记为
。



