ABSTRACT

Let $\beta =\frac{\sqrt{5}+1}{2}$ , T is the continued β-fraction transformation on [0,1), and $\frac{p_n\left(x\right)}{q_n\left(x\right)}$ is the nth-order β-fraction-convergent of x. In this paper, we show many properties of the sequence ${\left(\frac{p_n\left(x\right)}{q_n\left(x\right)}\right)}_{n\ge 1}$ . Moreover, we prove that ${\left(\frac{p_n\left(x\right)}{q_n\left(x\right)}\right)}_{n\ge 1}$ converges to x.

Keywords:Continued β-Fraction, Convergent, Converges

β-连分数的渐近分数

肖倩

华南理工大学，广东 广州

收稿日期：2018年12月2日；录用日期：2018年12月21日；发布日期：2018年12月28日

摘 要

设 $\beta =\frac{\sqrt{5}+1}{2}$ ，T为[0,1)上的β-连分数变换， $\frac{p_n\left(x\right)}{q_n\left(x\right)}$ 是x的n阶β-渐近分数。本文证明了序列 ${\left(\frac{p_n\left(x\right)}{q_n\left(x\right)}\right)}_{n\ge 1}$ 的一些性质，并且证明了 ${\left(\frac{p_n\left(x\right)}{q_n\left(x\right)}\right)}_{n\ge 1}$ 收敛且收敛到x。

关键词 :β-连分数，渐近分数，收敛

Copyright © 2018 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

在1957年，数的表示理论中一种新的表示方法——β-展开被Renyi [1] 首次提出。之后，β-展式的丢番图理论和遍历性质被很多人深入研究。令β是大于1的任何实数，定义β-变换 $T_{\beta }:\left[0,1\right)\to \left[0,1\right)$

$T_{\beta }\left(x\right)=\beta x-\lfloor \beta x\rfloor =\left\{\beta x\right\}$ , $x\in \left[0,1\right)$ ,

其中 $\lfloor x\rfloor$ 表示不超过x的最大整数， $\left\{x\right\}$ 表示数x的小数部分。

那么，任意一个实数 $x\in \left[0,1\right)$ 都可以把它展成一个如下形式的有限或者无限的序列：

对于任意的 $n\ge 1$ ， ${\epsilon }_1\left(x\right)=\lfloor \beta x\rfloor$ ， ${\epsilon }_{n+1}\left(x\right)={\epsilon }_1\left(T_{\beta }^n\left(x\right)\right)$ 。我们把式叫做x的β-展式，记为序列 $\epsilon \left(x,\beta \right):=\left({\epsilon }_1\left(x\right),{\epsilon }_2\left(x\right),\cdots ,{\epsilon }_n\left(x\right),\cdots \right)$ [2] 。而且，Parry [3] 刻画了序列可允许性。之后，我们又了解到当 $\beta \in \mathbb{N}$ ，x的β-展式是最终周期的当且仅当 $x\in \mathbb{Q}$ 。设是一个Pisot数，那么x的β-展式是最终周期的当且仅当 $x\in \mathbb{Q}\left(\beta \right)\cap \left[0,1\right)$ (其中 $\mathbb{Q}\left(\beta \right)$ 是表示包含 $\mathbb{Q}$ 和β的最小的域) [4] [5] 。

任意实数x可以唯一地被展成 ${{{\displaystyle \sum }}^{\text{}}}_{k=0}^n{v}_{-k}{\beta }^k+{{{\displaystyle \sum }}^{\text{}}}_{k=1}^{\infty }{v}_k{\beta }^{-k}$ 。在求和中β的非负幂部分叫做x的β-整数部分，记作 ${\lfloor x\rfloor }_{\beta }$ ；β的负幂部分叫做x的β-分数部分，记作 ${\left\{x\right\}}_{\beta }$ 。如果x的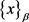为0，即只有β的非负幂部分，我们把x叫做β-整数。用 ${\mathbb{Z}}_{\beta }^{+}$ 来表示所有的β-整数的集合，也就是说

${\mathbb{Z}}_{\beta }^{+}=\left\{所有的非负\beta -整数\right\}=\left\{\xi :\exists x\ge 0,s.t.\xi ={\lfloor x\rfloor }_{\beta }\right\}$ 。

当 $\beta =\frac{\sqrt{5}+1}{2}$ 时，我们知道

${\mathbb{Z}}_{\beta }^{+}=\left\{m+n\beta |m,n\in \mathbb{Z},m,n\ge 0,-1<m-\frac{n}{\beta }<\beta \right\}$ [6] 。

定义1.1：定义 $T:\left[0,1\right)\to \left[0,1\right)$

$T\left(0\right):=0$ , $T\left(x\right)=\frac{1}{x}-{\lfloor \frac{1}{x}\rfloor }_{\beta }$ , $x\in \left(0,1\right)$ ,

其中 ${\lfloor x\rfloor }_{\beta }$ 表示不超过x的最大β-整数。

因此，对于任意的非负实数x都有如下形式的β-连分数展式：

$x={\lfloor x\rfloor }_{\beta }+\frac{1}{{\lfloor \frac{1}{x}\rfloor }_{\beta }+\frac{1}{{\lfloor \frac{1}{T\left(x\right)}\rfloor }_{\beta }+\cdots +\frac{1}{{\lfloor \frac{1}{T^{K-1}\left(x\right)}\rfloor }_{\beta }+T^k\left(x\right)}}}:=\left[a_0\left(x\right);a_1\left(x\right),a_2\left(x\right),\cdots ,a_k\left(x\right)+T^k\left(x\right)\right]$ ,

$={\lfloor x\rfloor }_{\beta }+\frac{1}{{\lfloor \frac{1}{x}\rfloor }_{\beta }+\frac{1}{{\lfloor \frac{1}{T\left(x\right)}\rfloor }_{\beta }+\cdots }}:=\left[a_0\left(x\right);a_1\left(x\right),a_2\left(x\right),\cdots \right]$ ,

其中 $a_0\left(x\right)={\lfloor x\rfloor }_{\beta },a_i\left(x\right)={\lfloor \frac{1}{T^{i-1}\left(x\right)}\rfloor }_{\beta },i\ge 1$ 。

2. 定理及证明

定义2.1：给定β是大于1的任意实数，对任意的 $n\ge 1$ ， $a_n\in {\mathbb{Z}}_{\beta }^{+}$ ，令 $p_{-1}=1$ ， $q_{-1}=0$ ， $p_0=a_0$ ， $q_0=1$ ，定义

$p_n=a_n{p}_{n-1}+p_{n-2}$

对于任意的 $x=\left[a_0;a_1,a_2,\cdots \right]\in {ℝ}^{+}$ ，把 $\frac{p_n\left(x\right)}{q_n\left(x\right)}$ 叫做x的n阶β-渐近分数。

注2.2：由上述定义可以看出：由于 $a_n\ge 1$ ，故序列 ${\left(q_n\right)}_{n\ge 1}$ 单调递增且

$q_n=a_n{q}_{n-1}+q_{n-2}\ge 2q_{n-2}\ge \cdots \ge 2^{\frac{n-2}{2}}$ 。

命题2.3：对任意的 $n\ge 1$ ，我们有

$p_n{q}_{n-1}-q_n{p}_{n-1}={\left(-1\right)}^{n-1}$ 。

证明：把定义2.1中式的左右同时乘以 $q_{n-1}$ ，便得到

$p_n{q}_{n-1}=a_n{p}_{n-1}{q}_{n-1}+p_{n-2}{q}_{n-1}$ ，

类似的，把式的左右两边同时乘以 $p_{n-1}$ ，便得到

$q_n{p}_{n-1}=a_n{q}_{n-1}{p}_{n-1}+q_{n-2}{p}_{n-1}$ 。

那么可得 $p_n{q}_{n-1}-q_n{p}_{n-1}=p_{n-2}{q}_{n-1}-q_{n-2}{p}_{n-1}=\cdots ={\left(-1\right)}^{n-1}$ 。

推论2.4：对任意的 $n\ge 1$ ，有

$\frac{p_n}{q_n}-\frac{p_{n-1}}{q_{n-1}}=\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}$ 。

证明：把命题2.3中的式子左右两边同时除以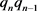便可得到

$\frac{p_n}{q_n}-\frac{p_{n-1}}{q_{n-1}}=\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}$ 。

注2.5：由推论2.4可以看出，每一个奇数阶的β-渐近分数都大于紧接着它的那个偶数阶的β-渐近分数。

命题2.6：对任意的 $n\ge 1$ ，有

$q_n{p}_{n-2}-p_n{q}_{n-2}={\left(-1\right)}^{n-1}{a}_n$ 。

证明：把定义2.1中式的左右两边同时乘以 $q_{n-2}$ ，便得到

$p_n{q}_{n-2}=a_n{p}_{n-1}{q}_{n-2}+p_{n-2}{q}_{n-2}$ ，

同样的把式的左右两边同时乘以 $p_{n-2}$ ，便得到

$q_n{p}_{n-2}=a_n{q}_{n-1}{p}_{n-2}+q_{n-2}{p}_{n-2}$ 。

那么可得 $q_n{p}_{n-2}-p_n{q}_{n-2}=a_n\left(p_{n-2}{q}_{n-1}-q_{n-2}{p}_{n-1}\right)$ 。再由命题2.3得到： $q_n{p}_{n-2}-p_n{q}_{n-2}={\left(-1\right)}^{n-1}{a}_n$ 。

推论2.7：对任意的 $n\ge 1$ ，有

$\frac{p_{n-2}}{q_{n-2}}-\frac{p_n}{q_n}=\frac{{\left(-1\right)}^{n-1}{a}_n}{q_n{q}_{n-2}}$ 。

证明：把命题2.6的左右两边同时除以 $q_n{q}_{n-2}$ 得到：

$\frac{p_{n-2}}{q_{n-2}}-\frac{p_n}{q_n}=\frac{{\left(-1\right)}^{n-1}{a}_n}{q_n{q}_{n-2}}$ 。

注2.8：由推论2.7可以看出，偶数阶的β-渐近分数形成递增序列，奇数阶的β-渐近分数形成递减序列。显然，把推论2.4和推论2.7结合得到：任何奇数阶的β-渐近分数必大于任何偶数阶的β-渐近分数。

定理2.9：对任意的 $n\ge 1$ ，序列 ${\left(\frac{p_n\left(x\right)}{q_n\left(x\right)}\right)}_{n\ge 1}$ 收敛。

证明：由推论2.4可知：

$\begin{array}{c}\frac{p_n}{q_n}=\frac{p_{n-1}}{q_{n-1}}+\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}=\frac{p_{n-2}}{q_{n-2}}+\frac{{\left(-1\right)}^{n-2}}{q_{n-1}{q}_{n-2}}+\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}=\cdots \\ =\frac{p_0}{q_0}+\frac{1}{q_0{q}_1}+\frac{-1}{q_1{q}_2}+\cdots +\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}=a_0+\frac{1}{q_0{q}_1}+\frac{-1}{q_1{q}_2}+\cdots +\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}\end{array}$

因为 $\frac{1}{q_0{q}_1}+\frac{-1}{q_1{q}_2}+\cdots +\frac{{\left(-1\right)}^{n-1}}{q_n{q}_{n-1}}+\cdots$ 是交错级数，由Libniz判别法知级数收敛，即 ${\lim }_{n\to \infty }\frac{p_n\left(x\right)}{q_n\left(x\right)}$ 存在，故序列 ${\left(\frac{p_n\left(x\right)}{q_n\left(x\right)}\right)}_{n\ge 1}$ 收敛。

命题2.10： [7] 对于任意的 $x\in {ℝ}^{+}$ ， $n\ge 0$ ，那么有

$x=\frac{p_n\left(x\right)+p_{n-1}\left(x\right)T^n\left(x\right)}{q_n\left(x\right)+q_{n-1}\left(x\right)T^n\left(x\right)}$ 。

定理2.11：设 $\frac{p_n\left(x\right)}{q_n\left(x\right)}$ 是x的n阶β-渐近分数，则。

证明：

。

当n趋于无穷时， $2^{3-n}$ 趋于0，因此 $\frac{p_n\left(x\right)}{q_n\left(x\right)}\to x$ 。

文章引用

肖 倩. β-连分数的渐近分数
The Convergent in Continued β-Fraction[J]. 应用数学进展, 2018, 07(12): 1645-1649. https://doi.org/10.12677/AAM.2018.712192

参考文献