Computer Science and Application
Vol.
13
No.
04
(
2023
), Article ID:
64736
,
8
pages
10.12677/CSA.2023.134089
基于S型传递函数的二进制乌鸦搜索算法求解0-1背包问题
高泽贤1,2,张寒崧1,2,孙菲1,2,王丽娜1,2
1河北地质大学信息工程学院,河北 石家庄
2河北地质大学大数据与计算智能实验室,河北 石家庄
收稿日期:2023年3月22日;录用日期:2023年4月21日;发布日期:2023年4月28日

摘要
基于传递函数,我们提出了一种新的二进制乌鸦搜索算法(BCSA)来求解0-1背包问题(0-1KP),它不仅保留了原有乌鸦搜索算法良好的探索能力,而且具有良好的开发能力。充分利用修复优化方法处理不可行解,在提升算法搜索能力的同时,也加快了算法的收敛速度。为验证BCSA求解0-1KP的性能,将其计算结果与七种不同算法的计算结果进行了比较,发现BCSA的求解精度高、算法稳定性良好,非常适合用来处理大规模0-1KP实例。
关键词
演化算法,乌鸦搜索算法,转换函数,0-1背包问题

Binary Crow Search Algorithm Based on S-Type Transfer Function for Solving 0-1 Knapsack Problem
Zexian Gao1,2, Hansong Zhang1,2, Fei Sun1,2, Li’na Wang1,2
1College of Information Technology, Hebei GEO University, Shijiazhuang Hebei
2College of Big Data & Computing Intelligence Laboratory, Hebei GEO University, Shijiazhuang Hebei
Received: Mar. 22nd, 2023; accepted: Apr. 21st, 2023; published: Apr. 28th, 2023

ABSTRACT
Based on the transfer function, we propose a new Binary Crow Search Algorithm (BCSA) for solving the 0-1 Knapsack Problem (0-1KP). It not only retains the good exploration ability of the original crow search algorithm, but also has good development ability. Making full use of repair optimization methods to handle infeasible solutions improves the search ability of the algorithm while also accelerating its convergence speed. In order to verify the performance of BCSA in solving 0-1KP, its calculation results were compared with those of seven different algorithms. It was found that BCSA has high resolution and good algorithm stability, and is very suitable for processing large-scale 0-1KP instances.
Keywords:Evolutionary Algorithm, Crow Search Algorithm, Conversion Function, 0-1 Knapsack Problem

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
背包问题(Knapsack Problem, KP) [1] 是一种重要的组合优化问题,同时也是一类经典的NP完全问题。它在诸多领域具有广泛的应用价值,例如:资金预算、资源分配、装载问题、分布式系统、能量最小化等 [2] [3] [4] 。0-1KP问题是一种最基本的背包问题,属于NP类型的难题。0-1KP可以概括为:在满足背包载重限制的条件下,从多个具有价值系数和重量系数的物品中有选择地装入背包,以达到价值系数之和最大化。
目前,求解0-1背包问题的方法大体可分为精确求解法 [5] 和近似求解法两类。尽管精确算法的解的准确度很高,但是它的时间复杂度却属于伪多项式。随着0-1KP实例规模的增大,求解效率会越来越差。因此,在求解较大规模的0-1KP实例时,精确算法就不是最佳选择。非精确算法,特别是演化算法,可以有效缓解精确算法的局限性。在既要满足计算精度好,又要满足求解速度快的条件下,演化算法在求解0-1KP问题上受到了较高的认可 [1] 。
乌鸦搜索算法(CSA)是由Askarzadeh [6] 根据乌鸦的觅食行为提出的。乌鸦是一种拥有记忆力的群居鸟类,它们聪明灵巧,能将多余的食物藏起来,而且能够把藏起来的食物的最佳位置(Memory, M)牢牢记在脑海里。自CSA的提出以来,由于其控制参数少且易于实现等优点,在各个领域中获得了广泛应用。本文提出了一种应用于解决0-1KP问题的二进制乌鸦搜索算法,它在传统乌鸦搜索算法的基础上,采用传递函数进行离散化处理,进而通过实验与7种演化算法比较,证明了该算法求解此类实例的有效性。
2. 相关背景
2.1. KP的定义与数学模型
0-1KP的定义:给定n个物品的集合 和一个背包容量为C的背包,每一种物品i都有两个基本属性:价值属性和重量属性。物品的重量集合为 ,价值集合为 。故将0-1背包问题的数学模型描述如下:
(1)
s.t. (2)
(3)
当xi = 1时,表示第i项放入背包;当xi = 0时,表示第i项未被选取放入背包。
2.2. 乌鸦搜索算法
乌鸦是一种有着群居生活习性的鸟类,它们拥有聪明的头脑,能够记忆存储信息。从算法的角度来看,乌鸦代表搜索者,乌鸦种群的整个飞行区域代表搜索空间,每一只乌鸦的位置代表一个可行解。乌鸦位置的好坏,通过目标函数值来判断,环境中的最佳食物来源即为全局最优解。
为了便于阐述如何利用乌鸦搜索算法CSA求解连续优化问题,不失一般性,设maxf(X), 是最小数值优化问题。其中,lb和ub是个体X中每一维度分量的下界和上界。下面将对CSA的算法原理 [7] 进行详细介绍。
假设乌鸦的种群规模为N,最大迭代次数为MIT,问题的维度为d;第t次迭代时, 表示为乌鸦i的当前位置一个位置向量,其中 ; 。每一只乌鸦所找到的历史最优位置称为记忆位置。APi,t表示在第t次迭代乌鸦i的感知概率;fli,t表示第t次迭代时乌鸦i的飞行长度。乌鸦i会随机选择一只乌鸦j进行跟随,此时乌鸦j感到一定的威胁,通过引入感知概率来保护自己的食物被窃取。
CSA中的位置更新方式分为两种:当迭代时的发现概率小于感知概率时,即乌鸦j没有发现被乌鸦i跟踪,此时乌鸦i的位置更新公式为:
(4)
其中,xik(t+1)表示第i只乌鸦在当前迭代第k个维度时的位置,fl为乌鸦飞行长度,mjk(t)表示第j只乌鸦在第k维度的记忆值,rand表示是服从均匀分布的[0, 1]中的随机数。当迭代时的发现概率大于感知概率时,即乌鸦j发现了乌鸦i跟踪它,那么乌鸦j就会把乌鸦i愚弄到搜索空间中的一个任意位置,以保证自己的食物不被窃取。此时乌鸦的位置更新公式为:
(5)
综上所述,位置更新公式为:
(6)
当乌鸦的位置发生改变时,采用如下方式对乌鸦的记忆进行更新:
(7)
3. 二进制乌鸦搜索算法
原始的CSA算法是针对实数域上的连续优化问题提出来的,而求解0-1KP问题是组合优化问题,需要将实数域转化为离散域,因此本文采用传递函数进行离散化处理。常见的主流传递函数有S型和V型,本文使用S3 (如公式(8)所示),用于解决乌鸦搜索算法的离散化问题。
(8)
二进制乌鸦搜索算法(BCSA)是在基于CSA的基础上展开的,上节已经给出,本节不再赘述。现给出BCSA的伪代码。
设maxf(X), 是最小数值优化问题,参数d、N、MIT含义同上,不再重复。感知概率AP = 0.1,飞行长度fl = 2,rand[1, N]是随机选1到N之间的一个整数, 表示BCSA的最优个体,则将BCSA算法伪代码描述如下。
算法1 BCSA
输入:maxf(X)实例,参数d、N、MIT、AP、fl。
输出:最优个体B以及目标函数值f(B)。
1 随机初始化种群 , ;
2 GROA处理后,计算f(Xi(0))用于评价个体Xi(0), ,确定最优个体B;
3 初始化Xi(0)的记忆 ,即 , ;
4 for t←1 to MIT do
5 for i←1 to N do
6 j←rand[1, N];
7 if rand1(0, 1) > AP then
8 for k←1 to d do
9 根据公式(4)更新乌鸦Xi(t + 1)的位置;
10 end for
11 else
12 for k←1 to d do
13 根据公式(5)更新乌鸦Xi(t + 1)的位置;
14 end for
15 end if
16 利用公式(8)对乌鸦的位置进行离散化;
17 计算f(Xi(t + 1))用于评价新个体Xi(t + 1), ,确定最优个体B;
18 利用公式(7)更新乌鸦Mi(t+1)的记忆值;
19 end for
20 end for
21 return (B, f(B))。
4. 利用BCSA求解0-1KP
4.1. 个体编码与处理不可行解
在BCSA中,个体编码为 ,利用转换函数转换为 ,xi1 = 1表示物品被选择放入背包,反之,没有放入背包。
由于CSA中乌鸦的位置是由随机生成的向量决定的,解空间中会不可避免地出现不可行解,这就导致无法根据目标函数值来判断个体的适应性。一般而言,修复法、惩罚函数法以及修复和优化策略常常用来解决不可行解。本文采用了文献 [1] 中提出的修复优化方法(GROA)来解决过程中出现的不可行解的问题。
4.2. 求解过程以及算法流程图
采用BCSA算法求解0-1KP的具体步骤如下:首先需要对每个物品进行价值密度降序,并将排序后的结果保存在一维数组中;将乌鸦种群初始化为0-1向量,再利用GROA对种群中每个个体进行修复优化并排序,完成对乌鸦记忆的初始化;然后重复以下过程直到满足终止条件:随机选择一只乌鸦j进行跟踪,在感知概率一定的条件下,通过公式(6)对乌鸦的位置进行更新,利用传递函数进行离散化;接着利用GROA修复不可行解;通过公示(7)更新乌鸦记忆值;最后将最优解B输出。具体算法流程如图1所示。
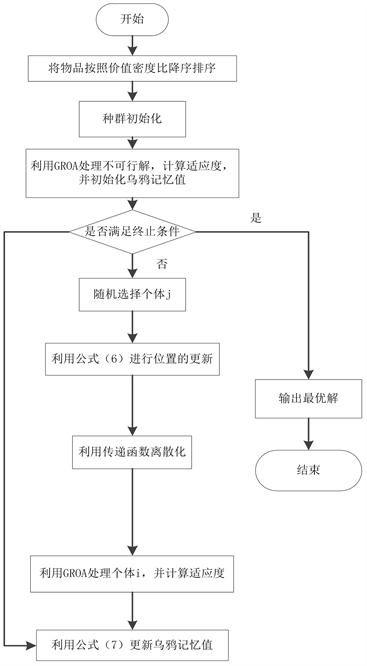
Figure 1. Flow chart of algorithm BCSA for solving 0-1KP
图1. 算法BCSA求解0-1KP的流程图
5. 计算结果与分析
本次实验所用的微型计算机:惠普笔记本,硬件环境为Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz 2.59 GHz,操作系统为Microsoft Windows 10。在Microsoft Visual Studio 2017编译环境中使用C语言编程。
5.1. 0-1KP实例与算法参数
实例可从https://pages.mtu.edu/~kreher/cages/Data.html获取。为了验证BCSA的性能,与求解相同实例的算法进行比较,这7个算法分别为:BTSA [8] 、BHHO [9] 、BWOA [10] 、BFFA [11] 、BPSO [12] 、BTLBO [13] 、BAOA [14] ,具体数据请查阅相关文献获取。
5.2. BCSA与其他算法的比较
本节中,将其他7个算法求解0-1KP的计算结果与BCSA的计算结果进行了比较;AVE和STD分别表示测试50次计算结果的平均值和标准差,其中未达到OPT的用蓝色标示;各算法的求解结果在表1、表2中给出。
由以下两表可知,BCSA在求解25个实例的结果中,就平均值来说,有24个实例能够达到最优值,BFFA和BHHO表现较差仅有18个实例达到最优,BCSA在8个算法中的排名第一;就标准差来说,BCSA在25个实例中,除了KP24d,其他实例的标准差都为0,而其他算法都存在较大的标准差。BCSA在求解精度以及算法稳定性方面远超其他算法。
Table 1. Results comparison for solving KP8a-KP12e instances
表1. 求解KP8a-KP12e实例的结果比较
Table 2. Results comparison for solving KP16a-KP24e instances
表2. 求解KP16a-KP24e实例的结果比较
6. 总结与展望
本文提出了一种以S型传递函数为基础的二进制乌鸦搜索算法BCSA,该算法可以有效地解决各类二元优化问题。通过对25个大规模0-1KP实例运用BCSA进行求解,与7种算法的求解结果进行比较,以此验证BCSA求解0-1KP的能力。经计算结果可知,BCSA在解0-1KP问题时,具备较高的精确度和稳定性,因此可以极大地提升解决这一问题的效率。此外,深入研究BCSA在其他组合优化问题(例如集合覆盖)的应用以及更加高效的离散化方法,也是值得我们持续探索的课题。
基金项目
河北省自然科学基金项目(项目编号:F2020403013),河北省高等学校科学技术研究项目(项目编号:ZD2021016)。
文章引用
高泽贤,张寒崧,孙 菲,王丽娜. 基于S型传递函数的二进制乌鸦搜索算法求解0-1背包问题
Binary Crow Search Algorithm Based on S-Type Transfer Function for Solving 0-1 Knapsack Problem[J]. 计算机科学与应用, 2023, 13(04): 915-922. https://doi.org/10.12677/CSA.2023.134089
参考文献
- 1. 王熙照, 贺毅朝. 求解背包问题的演化算法[J]. 软件学报, 2017, 28(1): 1-16.
- 2. 贺毅朝, 李泽文, 李焕哲, 等. 离散灰狼优化算法求解有界背包问题[J]. 计算机工程与设计, 2019, 40(4): 1008-1015.
- 3. Peng, H., Wu, Z.J., Shao, P. and Deng, C.S. (2016) Dichotomous Binary Differential Evolution for Knapsack Problems. Mathematical Problems in Engineering, 2016, Article ID: 5732489. https://doi.org/10.1155/2016/5732489
- 4. Müller, S., Al-Shatri, H., Wichtlhuber, M., Hausheer, D. and Klein, A. (2015) Computation Offloading in Wireless Multi-Hop Networks: Energy Minimization via Multi-Dimensional Knapsack Problem. 2015 IEEE 26th Annual International Sym-posium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, 30 August-2 September 2015, 1717-1722. https://doi.org/10.1109/PIMRC.2015.7343576
- 5. Song, H.J., Liang, C.G. and Can, G.G. (1999) Solving the 0/1-Knapsack Problem on Quantum Computer. Chinese Journal of Computers, 12, 1314-1316.
- 6. Askarzadeh, A. (2016) A Novel Metaheuristic Method for Solving Constrained Engineering Optimiza-tion Problems: Crow Search Algorithm. Computers & Structures, 169, 1-12. https://doi.org/10.1016/j.compstruc.2016.03.001
- 7. 刘雪静, 贺毅朝, 路凤佳, 等. 基于Lévy飞行的差分乌鸦算法求解折扣{0-1}背包问题[J]. 计算机应用, 2018, 38(2): 433-442.
- 8. Kaur, S., Awasthi, L.K., Sangal, A.L. and Dhiman, G. (2020) Tunicate Swarm Algorithm: A New Bio-Inspired Based Metaheuristic Paradigm for Global Op-timization. Engineering Applications of Artificial Intelligence, 90, Article ID: 103541. https://doi.org/10.1016/j.engappai.2020.103541
- 9. Heidari, A.A., Mirjalili, S., Faris, H., et al. (2019) Harris Hawks Optimization: Algorithm and Applications. Future Generation Computer Systems, 97, 849-872. https://doi.org/10.1016/j.future.2019.02.028
- 10. Mirjalili, S. and Lewis, A. (2016) The Whale Optimization Algo-rithm. Advances in Engineering Software, 95, 51-67. https://doi.org/10.1016/j.advengsoft.2016.01.008
- 11. Shayanfar, H. and Gharehchopogh, F.S. (2018) Farmland Fertility: A New Metaheuristic Algorithm for Solving Continuous Optimization Problems. Applied Soft Computing, 71, 728-746. https://doi.org/10.1016/j.asoc.2018.07.033
- 12. Kennedy, J. and Eberhart, R. (1995) Particle Swarm Op-timization. Proceedings of ICNN’95—International Conference on Neural Networks, Perth, 27 November-1 December 1995, 1942-1948. https://doi.org/10.1109/ICNN.1995.488968
- 13. Rao, R.V., Savsani, V.J. and Vakharia, D.P. (2011) Teaching-Learning-Based Optimization: A Novel Method for Constrained Mechanical Design Optimization Problems. Computer-Aided Design, 43, 303-315. https://doi.org/10.1016/j.cad.2010.12.015
- 14. Hashim, F.A., Hussain, K., Houssein, E.H., Mabrouk, M.S. and Al-Atabany, W. (2021) Archimedes Optimization Algorithm: A New Metaheuristic Algorithm for Solving Optimization Problems. Applied Intelligence, 51, 1531-1551. https://doi.org/10.1007/s10489-020-01893-z
