Advances in Applied Mathematics
Vol.06 No.04(2017), Article ID:21531,10
pages
10.12677/AAM.2017.64073
Special Linear Group SL(2,R) of Finite Abelian Subgroup
Chuanhua Jiang, Cuilian Duan
Guangxi Normal University, Guilin Guangxi

Received: Jul. 8th, 2017; accepted: Jul. 24th, 2017; published: Jul. 27th, 2017

ABSTRACT
In this paper, we study the finite Abelian subgroup of special linear group 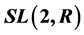 by using the eigenvalue theory of l-matrix and the solution method of constant coefficient linear homogeneous recursive relations. We get the structure of cyclic group for arbitrary order n of
by using the eigenvalue theory of l-matrix and the solution method of constant coefficient linear homogeneous recursive relations. We get the structure of cyclic group for arbitrary order n of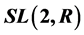 , that is to say, all the solutions of the 2 order matrix equation:
, that is to say, all the solutions of the 2 order matrix equation: 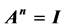 and
and 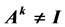 (
(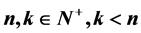 ) are given out. Furthermore, we hope to determine the structure of finite Abelian subgroup of special linear group
) are given out. Furthermore, we hope to determine the structure of finite Abelian subgroup of special linear group 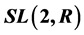 by discussing the commutativity between generators of arbitrary order cyclic group.
by discussing the commutativity between generators of arbitrary order cyclic group.
Keywords:Special linear Group, Abelian Group, Homogeneous Recurrence Relation, l- Matrix

特殊线性群SL(2,R)的有限Abelian子群
蒋传华,段翠连
广西师范大学,广西 桂林

收稿日期:2017年7月8日;录用日期:2017年7月24日;发布日期:2017年7月27日

摘 要
本文运用l-矩阵的相关理论和常系数线性齐次递归关系的求解方法,对特殊线性群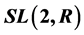 的有限Abelian子群进行了研究,给出了其任意阶循环群的结构,即2阶矩阵方程:
的有限Abelian子群进行了研究,给出了其任意阶循环群的结构,即2阶矩阵方程: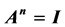 且
且 ,其中
,其中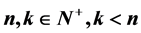 的全部解。进一步,我们希望通过探讨各阶循环群生成元的交换性来确定
的全部解。进一步,我们希望通过探讨各阶循环群生成元的交换性来确定 的有限Abelian子群结构。
的有限Abelian子群结构。
关键词 :特殊线性群,Abelian群,齐次递归关系,l-矩阵

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
n阶一般线性群是由n阶可逆矩阵组成的群,矩阵的元素取自R群运算,为通常的矩阵乘法,记为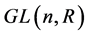 ;特殊线性群是
;特殊线性群是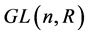 中行列式为1的全体矩阵,它们对于矩阵乘法构成
中行列式为1的全体矩阵,它们对于矩阵乘法构成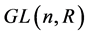 的一个子群,记为
的一个子群,记为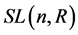 。一般线性群
。一般线性群 和特殊线性群
和特殊线性群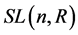 都是经典的李群,它们与群论和几何的研究有着密切的联系,在几何分析中有如下深刻的结果:特殊线性群
都是经典的李群,它们与群论和几何的研究有着密切的联系,在几何分析中有如下深刻的结果:特殊线性群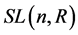 的有限Abelian子群是紧黎曼曲面的微分同胚不变量。这一结论将几何和代数(群理论)紧密联系起来,本文以此为出发点,结合群理论中对有限Abel群结构的完整刻画,如:有限Abel群可以分解成阶为素数的方幂的循环群(循环p-群)的直积 [1] 等,对特殊线性群
的有限Abelian子群是紧黎曼曲面的微分同胚不变量。这一结论将几何和代数(群理论)紧密联系起来,本文以此为出发点,结合群理论中对有限Abel群结构的完整刻画,如:有限Abel群可以分解成阶为素数的方幂的循环群(循环p-群)的直积 [1] 等,对特殊线性群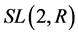 的有限Abelian子群进行研究,从而进一步加深对紧黎曼曲面的认识。
的有限Abelian子群进行研究,从而进一步加深对紧黎曼曲面的认识。
2. 基本概念、定理和方法
2.1. 基本概念和定理
下面列出一些与群和矩阵相关的概念和定理(可参考文献 [1] [2] ),方便后面章节使用。
定义2.1.1 [1] 设G为非空集合,“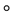 ”为G上的一个代数运算,若G的运算满足:
”为G上的一个代数运算,若G的运算满足:
1) “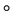 ”满足结合律,即
”满足结合律,即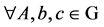 ,都有
,都有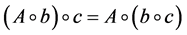 ;
;
2) G中有元素e,使对每个元 ,有
,有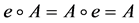 ;
;
3) 对G中每个元素A,存在元素 ,使得
,使得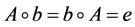 。
。
则G关于运算“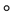 ”构成一个群(Group),记为
”构成一个群(Group),记为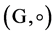 ,在不产生混淆的前提下,简记为G。
,在不产生混淆的前提下,简记为G。
定义2.1.2 [1] 如果对群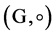 中任两个元素A,b均有
中任两个元素A,b均有
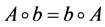 ,
,
即G的代数运算满足交换律,则称G为交换群(commutative Group)或Abel群(Abelian Group)。
定义2.1.3 [1] 群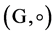 中的元素个数叫做群G的阶(order),记为
中的元素个数叫做群G的阶(order),记为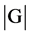 。如果
。如果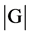 有限,称G为有限群(Finite Group),特别地,当
有限,称G为有限群(Finite Group),特别地,当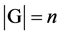 时,称G为n阶群,否则称G为无限群(infinite Group)。
时,称G为n阶群,否则称G为无限群(infinite Group)。
定义2.1.4 [1] 设G为群,H是G的一个非空子集,如果H关于G的运算也构成群,则称H为G的一个子群(subgroup),记作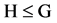 。
。
定义2.1.5 [1] 元素在实数域r中全体n阶可逆矩阵对于矩阵的乘法构成一个群,这个群记为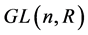 ,称为n阶一般线性群,
,称为n阶一般线性群,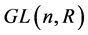 中全体行列式为1的矩阵对于矩阵的乘法也构成一个群,这个群记为
中全体行列式为1的矩阵对于矩阵的乘法也构成一个群,这个群记为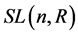 ,称为n阶特殊线性群。特别地,当n = 2时有
,称为n阶特殊线性群。特别地,当n = 2时有
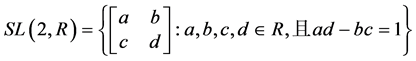 .
.
定义2.1.6 [1] 设G为群,如果存在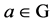 时
时
 ,
,
则称G为循环群,并称A是群G的一个生成元(Generator)。习惯上记为 ,当G中的元素个数是无限时,称G为无限循环群;当G中元素的个数为n时,称G为n阶循环群。
,当G中的元素个数是无限时,称G为无限循环群;当G中元素的个数为n时,称G为n阶循环群。
定义2.1.7 [1] 一般地,我们称下列形式矩阵为多项式矩阵,或l-矩阵:
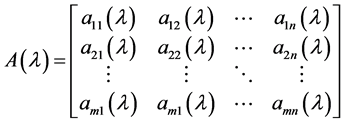
其中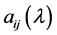 是以
是以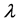 为未定元的数域k上的多项式。l-矩阵的加法、数乘及乘法与数域上的矩阵运算一样,只需在运算过程中将数的运算代之以多项式运算即可。
为未定元的数域k上的多项式。l-矩阵的加法、数乘及乘法与数域上的矩阵运算一样,只需在运算过程中将数的运算代之以多项式运算即可。
定义2.1.8 [2] 设 是一个n阶l-矩阵,k是小于等于n的某个自然数。如果
是一个n阶l-矩阵,k是小于等于n的某个自然数。如果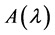 的所有k阶子式的最大公因子(它是首一多项式)不等于零,则称这个多项式为
的所有k阶子式的最大公因子(它是首一多项式)不等于零,则称这个多项式为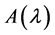 的k阶行列式因子,记为
的k阶行列式因子,记为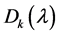 ,若
,若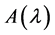 的所有k阶子式都等于零,则规定
的所有k阶子式都等于零,则规定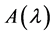 的k阶行列式因子等于零。
的k阶行列式因子等于零。
定义2.1.9 [2] 设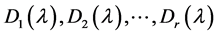 是l-矩阵
是l-矩阵 的非零行列式因子,则
的非零行列式因子,则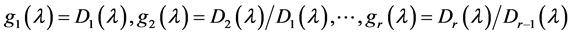 称为
称为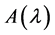 的不变因子。
的不变因子。
定义2.1.10 [2] 若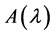 ,
,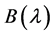 都是
都是 矩阵且
矩阵且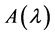 经过初等变换后可变为
经过初等变换后可变为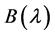 ,则称
,则称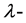 矩阵
矩阵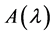 与
与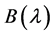 相抵。
相抵。
定理2.1.1 [2] 设A是数域k上的n阶矩阵,则A的特征矩阵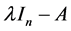 必相抵于
必相抵于
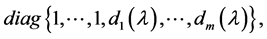
其中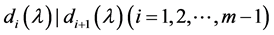 。
。
定理2.1.2 [2] 下列r阶矩阵
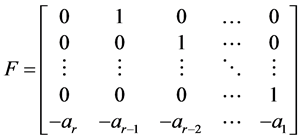
的行列式因子等于
 ,
,
其中共有r − 1个1,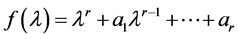 ,F的不变因子组也由
,F的不变因子组也由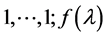 给出。
给出。
定理2.1.3 [2] 设A是数域k上的n阶方阵,A的不变因子组为
 ,
,
其中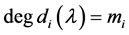 ,则A相似于下列分块对角矩阵:
,则A相似于下列分块对角矩阵:
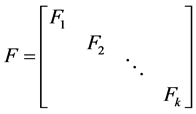
其中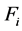 的阶等于
的阶等于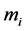 ,且
,且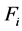 是形如定理2.1.2的矩阵,
是形如定理2.1.2的矩阵, 的最后一行由
的最后一行由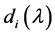 系数(除最高次项)的负值组成。
系数(除最高次项)的负值组成。
2.2. 常系数线性齐次递归关系的求解方法 [3]
本节我们介绍常系数线性齐次递归关系的求解,相关内容请参考文献 [3] 。
常系数线性齐次递归关系,其形如
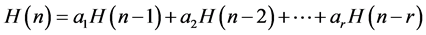
或
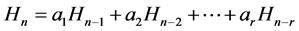 (2.2.1)
(2.2.1)
这里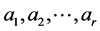 全部是常系数。例如
全部是常系数。例如
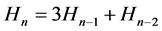
就是一个常系数线性齐次递归方程。假定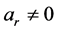 ,则递归关系(2.2.1)称为是r阶的。为了不失一般性,如果序列中r个相邻的H值
,则递归关系(2.2.1)称为是r阶的。为了不失一般性,如果序列中r个相邻的H值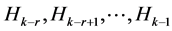 对某一k已知,则可用(2.2.1)算出
对某一k已知,则可用(2.2.1)算出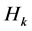 的值,于是
的值,于是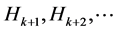 的值也可递归地算出。这就推出,(2.2.1)的解唯一地由r个相邻的H值(边界条件)所决定。因此,(2.2.1)的解的一般形式包含有r个待定常数,这些常数可由序列中相邻的r个H值来决定。我们把(2.2.1)改写成如下形式
的值也可递归地算出。这就推出,(2.2.1)的解唯一地由r个相邻的H值(边界条件)所决定。因此,(2.2.1)的解的一般形式包含有r个待定常数,这些常数可由序列中相邻的r个H值来决定。我们把(2.2.1)改写成如下形式
 (2.2.2)
(2.2.2)
这里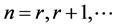 。
。
我们把与递归关系(2.2.1)或(2.2.2)相联系的方程
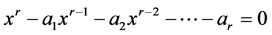 (2.2.3)
(2.2.3)
称为(2.2.1)或(2.2.2)的特征方程。方程(2.2.3)有r个根 ,这些根称为方程(2.2.1)的特征根。因为
,这些根称为方程(2.2.1)的特征根。因为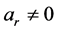 ,这些特征根必定全不为零。这些根可能是互异的,也可能有重根,还有可能是复根。关于常系数线性齐次递归关系的求解如下:
,这些特征根必定全不为零。这些根可能是互异的,也可能有重根,还有可能是复根。关于常系数线性齐次递归关系的求解如下:
1) 若特征方程有r个不同的特征根
定理设递归关系
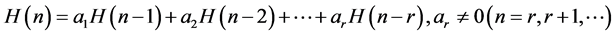 的特征根
的特征根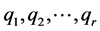 互不相同,则
互不相同,则
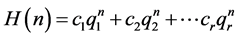
是一般解。
2) 若特征方程有重根
定理设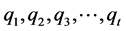 是递归关系
是递归关系
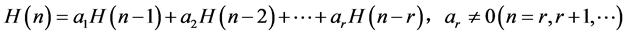
的特征方程互异的根。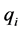 是特征方程的
是特征方程的 重根
重根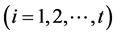 ,那么这个递归关系对应
,那么这个递归关系对应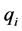 部分的一般解是
部分的一般解是
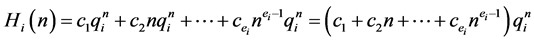
而这个递归关系的一般解是
 .
.
3) 若特征方程出现复根
当特征方程的诸系数是实数,但某些特征根是复数时,齐次解则写成另一种形式。因为复数根总是成对出现的,故设
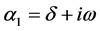 ,
, 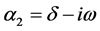
是一对共轭复根,则对应的齐次解为
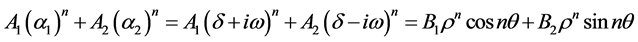
其中,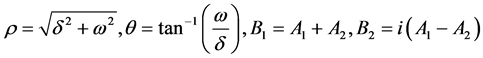
注意,这里的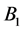 和
和 是由边界条件决定的常数。
是由边界条件决定的常数。
3. SL(2, R)的有限Abelian子群的结构
由群理论相关的结论我们有:有限循环群一定是有限Abelian群,故我们可以先寻找到特殊线性群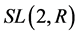 的有限循环子群,即对任意的
的有限循环子群,即对任意的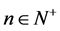 ,我们需要找到所有满足条件
,我们需要找到所有满足条件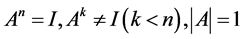 的矩阵。
的矩阵。
3.1. 特殊例子的讨论
由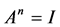 ,知A的特征根满足
,知A的特征根满足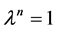 ,其特征根集为
,其特征根集为
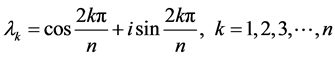 . [4]
. [4]
(此处A的特征根解集参考文献 [4] )
特别地,就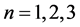 我们有如下的结论:
我们有如下的结论:
1) 当n=1时,若要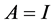 ,则A为单位阵;
,则A为单位阵;
2) 当n=2时,若要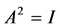 ,
,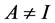 且
且 ,则此时无解。分析如下:
,则此时无解。分析如下:
① 考虑特征值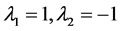 ,A特征多项式为
,A特征多项式为 ,
,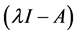 的2阶行列式因子就是矩阵A的特征多项式
的2阶行列式因子就是矩阵A的特征多项式 ,由定理2.1.1可以得到
,由定理2.1.1可以得到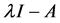 相抵于
相抵于 ,矩阵A的不变因子为
,矩阵A的不变因子为
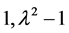 .
.
于是,由定理2.1.3,矩阵A的有理标准型为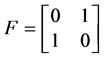 ,即
,即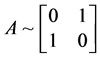 ,此时
,此时 ,不符合
,不符合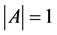 之要求。
之要求。
② 考虑特征值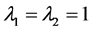 ,其特征多项式为
,其特征多项式为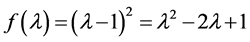 ,
,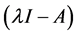 的2阶行列式因子就是矩阵A的特征多项式
的2阶行列式因子就是矩阵A的特征多项式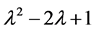 ,于是由定理2.1.1可以得到
,于是由定理2.1.1可以得到 相抵于
相抵于 ,矩阵A的不变因子为
,矩阵A的不变因子为
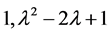 .
.
由定理2.1.3,矩阵A的有理标准型为 ,即
,即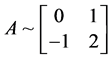 ,此时
,此时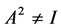 ,也不符合要求。
,也不符合要求。
③ 考虑特征值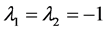 ,其特征多项式为
,其特征多项式为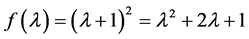 ,
,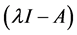 的2阶行列式因子就是矩阵A的特征多项式为
的2阶行列式因子就是矩阵A的特征多项式为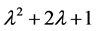 ,由定理2.1.1可以得到
,由定理2.1.1可以得到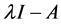 相抵于
相抵于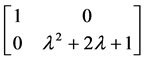 ,矩阵A的不变因子为
,矩阵A的不变因子为
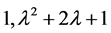 .
.
由定理2.1.3,矩阵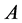 的有理标准型为
的有理标准型为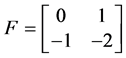 ,即
,即 ,此时
,此时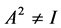 ,也不符合要求。
,也不符合要求。
3) 当n = 3时,要求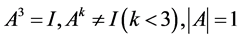 ,此时有解
,此时有解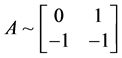 。分析如下:
。分析如下:
由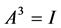 知矩阵A的特征值为
知矩阵A的特征值为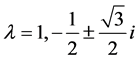
① 当 时,讨论的情况与
时,讨论的情况与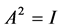 相同,可知此时无解。
相同,可知此时无解。
② 当 时(复根成对出现,相互共轭),A的特征多项式为
时(复根成对出现,相互共轭),A的特征多项式为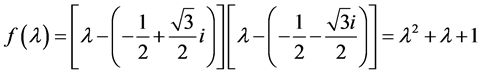 ,
,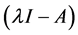 的2阶行列式因子就是矩阵A的特征多项式
的2阶行列式因子就是矩阵A的特征多项式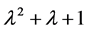 ,由定理2.1.1可以得到
,由定理2.1.1可以得到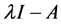 相抵于
相抵于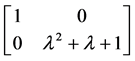 ,矩阵A的不变因子为
,矩阵A的不变因子为
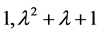
由定理2.1.3,矩阵A的有理标准型为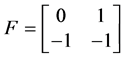 ,即
,即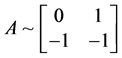 ,满足条件
,满足条件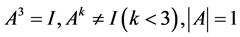 ,为我们所求的解。
,为我们所求的解。
3.2. 一般形式的归纳和证明
3.2.1. 一般情形的讨论
下面考虑 的情形。通过对
的情形。通过对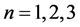 的特殊情形进行的讨论,我们发现一般情形下的讨论可以类似的进行,主要从特征根(复根成共轭对)入手,结合相关的定理(定理2.1.1、定理2.1.3),通过解常系数线性齐次递归方程最终给出一般情形下的结果。
的特殊情形进行的讨论,我们发现一般情形下的讨论可以类似的进行,主要从特征根(复根成共轭对)入手,结合相关的定理(定理2.1.1、定理2.1.3),通过解常系数线性齐次递归方程最终给出一般情形下的结果。
考虑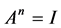 (
(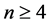 ),此时若A存在一组共轭特征根
),此时若A存在一组共轭特征根 和
和 ,这里
,这里  (若
(若 为偶数,则
为偶数,则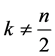 ),则A的特征多项式为
),则A的特征多项式为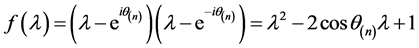 ,
,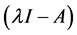 的2阶行列式因子就是A的特征多项式
的2阶行列式因子就是A的特征多项式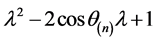 ,于是由定理2.1.1可以得到
,于是由定理2.1.1可以得到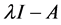 相抵于
相抵于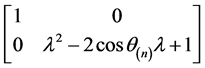 ,A的不变因子为
,A的不变因子为
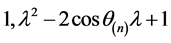 .
.
由定理2.1.3,A的有理标准型为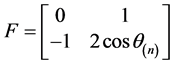 ,即
,即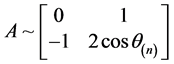 ,此时有
,此时有 ,由前面的讨论我们知道,若能证明F满足
,由前面的讨论我们知道,若能证明F满足 ,则可以得到
,则可以得到 。
。
3.2.2. 的证明
的证明
证明:由于矩阵A的特征多项式为 ,而
,而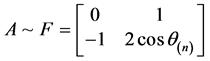 ,故
,故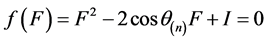 ,即
,即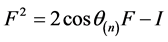 ,不妨令
,不妨令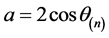 ,则:
,则:
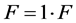 (1)
(1)
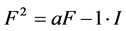 , (2)
, (2)
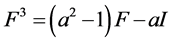 , (3)
, (3)
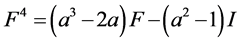 , (4)
, (4)
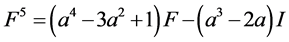 , (5)
, (5)
经过观察我们发现,等式(2)中F的系数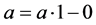 ,等式(3)中F的系数
,等式(3)中F的系数 ,等式(4)中F的系数
,等式(4)中F的系数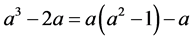 ,等式(5)中F的系数
,等式(5)中F的系数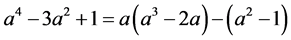 ,我们把每一等式中F的系数看成数列
,我们把每一等式中F的系数看成数列 中的元素则有:
中的元素则有: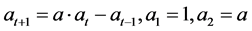 。这是一个常系数线性齐次递归方程,故根据相应的常系数线性齐次递归关系的求解方法,我们可以解得
。这是一个常系数线性齐次递归方程,故根据相应的常系数线性齐次递归关系的求解方法,我们可以解得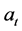 ,过程如下:
,过程如下:
由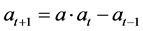 可以得到它的特征方程为
可以得到它的特征方程为
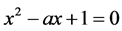 ,
,
因为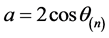 ,
,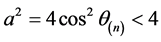 ,所以
,所以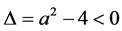 ,由常系数线性齐次递归关系可知,特征方程存在2个复根
,由常系数线性齐次递归关系可知,特征方程存在2个复根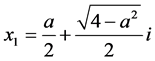 ,
,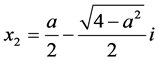 则
则
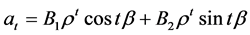 ,其中
,其中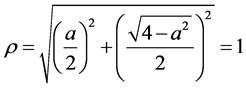 ,
,
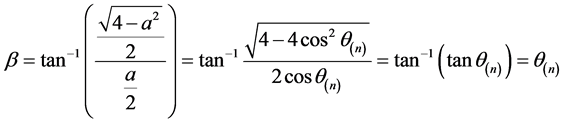 ,
,
所以 ,把
,把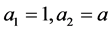 代入
代入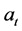 得:
得:
 ,
,
解之得:
 ,
,
故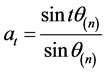 ,(
,(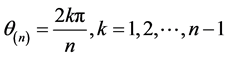 且若
且若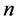 为偶数,则
为偶数,则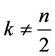 ),
),
从而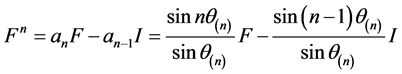 ,即有
,即有
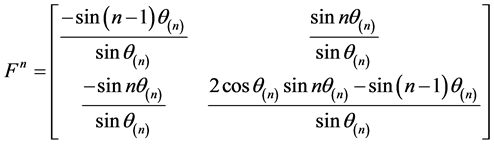 ,
,
由和差化积公式得:
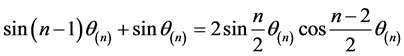 ,
,
又
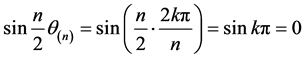 ,
,
所以
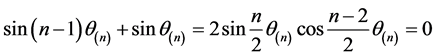 .
.
即
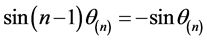 ,
,
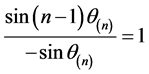 ,
,
又
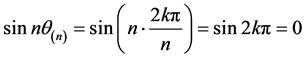 ,
,
所以
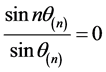 ,
,
故
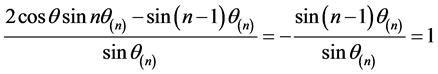 ,
,
从而 ,证毕。
,证毕。
3.2.3. SL(2, R)的有限循环子群的结构
由前面的讨论,我们已经找到了满足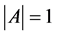 且
且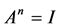 的所有矩阵,即:
的所有矩阵,即: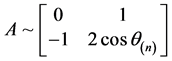 ,进一步为了在这些矩阵中找出符合条件
,进一步为了在这些矩阵中找出符合条件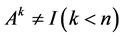 的矩阵,我们需要确定符合条件
的矩阵,我们需要确定符合条件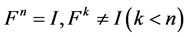 的
的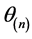 。
。
例如,当 时,
时,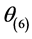 的取值为
的取值为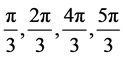 ,其中
,其中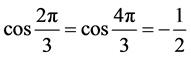 ,
,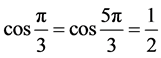 ,
,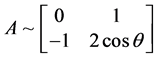 ,解得
,解得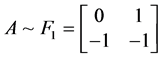 和
和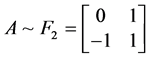 ,此时这两组解均满足
,此时这两组解均满足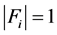 且
且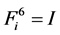 ,但对
,但对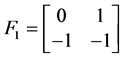 而言,有
而言,有 ,即
,即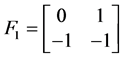 为
为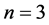 时的一个解,重复出现。下面我们找出符合条件
时的一个解,重复出现。下面我们找出符合条件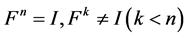 的所有
的所有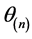 (
(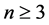 ),使得最后的结果不会重复,也不会遗漏。
),使得最后的结果不会重复,也不会遗漏。
对任意的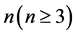 ,
,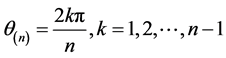 ,当k取
,当k取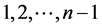 中不同的值时,
中不同的值时,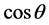 总会出现一对相同的值(仅有一对),如
总会出现一对相同的值(仅有一对),如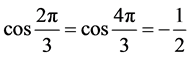 ,这是因为,若
,这是因为,若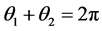 ,则
,则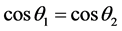 。由此我
。由此我
们可以缩小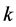 的取值范围。
的取值范围。
当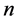 为奇数时,
为奇数时,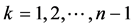 ,
,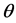 可取
可取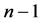 个值中,且首尾的值相加恰好等于
个值中,且首尾的值相加恰好等于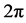 ,故我们只需取前
,故我们只需取前
面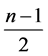 个值即可,即
个值即可,即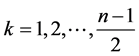 。由于n是奇数,而2k是偶数,所以
。由于n是奇数,而2k是偶数,所以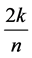 一定是一个最简分数,此时
一定是一个最简分数,此时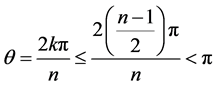 ,
,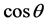 互不相等。
互不相等。
当 为偶数时,
为偶数时,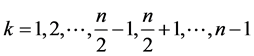 ,与前面的讨论类似,我们可以将
,与前面的讨论类似,我们可以将 的取值范围限定在前面
的取值范围限定在前面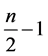 个值,即
个值,即 。进一步,由于2k是偶数时,而n也是偶数(不妨设
。进一步,由于2k是偶数时,而n也是偶数(不妨设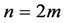 ),则有
),则有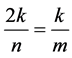 ,当k为奇数时,
,当k为奇数时, 是一个最简分数,不会导致解的重复;而当k为偶数时,由于
是一个最简分数,不会导致解的重复;而当k为偶数时,由于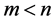 ,
,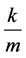 一定在前面的取值中出现过,从而导致解的重复,此时k只取
一定在前面的取值中出现过,从而导致解的重复,此时k只取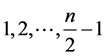 中奇数的那一部分值。
中奇数的那一部分值。
综上所述,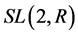 的有限Abelian子群中所有满足条件
的有限Abelian子群中所有满足条件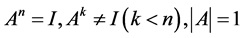 的矩阵如下:
的矩阵如下:
当n = 1时,则A为单位阵;
当n = 2时,则此时无解;
当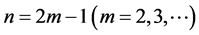 时,
时,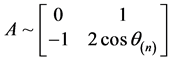 ,
,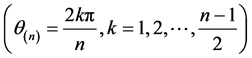 ;
;
当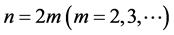 时,
时,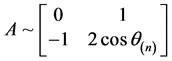 ,
,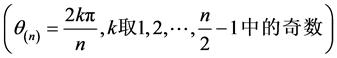 。
。
4. 进一步的问题
特殊线性群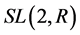 的3阶有限循环子群的生成元是
的3阶有限循环子群的生成元是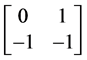 ,4阶有限循环子群的生成元是
,4阶有限循环子群的生成元是 ,5阶有限循环子群的生成元是
,5阶有限循环子群的生成元是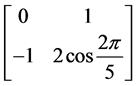 和
和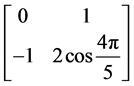 ,……,n阶有限循环子群的生成元是
,……,n阶有限循环子群的生成元是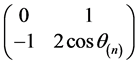 (
(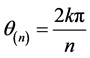 ,
, 取
取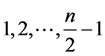 中的奇数),这些生成元所构成的循环子群能否做成特殊线性群
中的奇数),这些生成元所构成的循环子群能否做成特殊线性群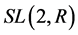 的子群的直积,目前本人还没有好的方法去解答,值得进一步探讨。
的子群的直积,目前本人还没有好的方法去解答,值得进一步探讨。
文章引用
蒋传华,段翠连. 特殊线性群SL(2,R)的有限Abelian子群
Special Linear Group SL(2,R) of Finite Abelian Subgroup[J]. 应用数学进展, 2017, 06(04): 627-636. http://dx.doi.org/10.12677/AAM.2017.64073
参考文献 (References)
- 1. 唐高华. 近世代数[M]. 北京: 清华大学出版社, 2008.
- 2. 姚慕生, 吴泉水. 高等代数学[M]. 第2版. 上海: 复旦大学出版社, 2008.
- 3. 杨振声. 组合数学及其算法[M]. 第3版. 合肥: 中国科学技术大学出版社, 2006.
- 4. 刘军成. GL(2, Z[i])的有限交换子群[J]. 湖北大学学报(自然科学版), 2010, 32(2): 233-240.