Advances in Applied Mathematics
Vol.
09
No.
09
(
2020
), Article ID:
37813
,
15
pages
10.12677/AAM.2020.99187
广义Fornberg-Whitham方程的某些非线性波解
朱贇,刘锐
华南理工大学,数学学院,广东 广州
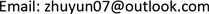
收稿日期:2020年9月1日;录用日期:2020年9月18日;发布日期:2020年9月25日

摘要
本文利用微分方程定性理论和动力系统分支方法寻找广义Fornberg-Whitham方程的非线性波解,当次数n = 2时,我们获得了四个非线性波解;当次数n = 3时,我们获得了一个非线性波解。
关键词
Fornberg-Whitham方程,行波系统,分支,精确解
Some Nonlinear Wave Solutions for the Generalized Fornberg-Whitham Equation
Yun Zhu, Rui Liu
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Sep. 1st, 2020; accepted: Sep. 18th, 2020; published: Sep. 25th, 2020

ABSTRACT
In this paper, the qualitative theory of differential equations and the bifurcation method of dynamical systems are used to find nonlinear wave solutions of the generalized Fornberg-Whitham equation. When n = 2, we obtained four nonlinear wave solutions. When n = 3, we obtained one nonlinear wave solution.
Keywords:Fornberg-Whitham Equation, Traveling Wave System, Bifurcation, Exact Solutions

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文利用微分方程定性理论和动力系统的分支方法 [1] [2] [3] [4] 研究n阶并带有参数b的广义Fornberg-Whitham (F-W)方程
(1)
方程(1)是F-W方程 [5] [6] 的广义形式,F-W方程具有如下形式
(2)
Fornberg和Whitham给出了方程(2)的一个尖孤立波解 ,其中A为任意常数 [7]。由于F-W方程不具有像Camassa-Holm (C-H)方程 [8]
(3)
这样完全可积和双Hamilton结构 [8] 等良好性质,一直并未引起广泛研究。直到近年来,F-W方程重新引起了大家的关注。
当b = 1,n = 2时,He和Meng等人给出了方程(1)的尖孤立波解 [9],Liang给出了精确的行波解 [10]。此外,Yang和Fan将F-W方程推广成二元F-W方程
(4)
并得到方程的光滑周期波、光滑孤立波和扭波等波解 [11]。Bi和Jiang研究了带线性色散项的F-W方程
(5)
证明了光滑和非光滑行波解的存在性,并给出了显示孤立波解 [12]。
本文主要研究当n = 2, 3时,方程(1)的某些非线性波解。
2. 主要结果
当n = 2时,令
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
1) 当 ,且 时, ,,, 是方程(1)的解;
2) 当 ,且 时, ,,, 是方程(1)的解;
3) 当 ,且 时, ,,, 是方程(1)的解;
4) 当 ,且 时, ,,, 是方程(1)的解。
当n = 3时,令
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)
, 由方程(27)决定
(27)
1) 当 ,且 时, 是方程(1)的解;
2) 当 ,且 时, 是方程(1)的解;
3) 当 ,且 时, 是方程(1)的解;
4) 当 ,且 时, 是方程(1)的解。
此外,我们已通过如下的Mathematica程序验证了由式子(12),(13),(14),(15),(26)分别给出的解 ,,,, 的正确性
具体推导如下。
3. 行波系统及首次积分
首先,对方程(1)做行波变换
(28)
其中 为常波速。
得到常微分方程
(29)
再将方程(29)进行积分一次,得到
(30)
其中,g为积分常数。
令
(31)
将(31)带入方程(30),得到平面系统
(32)
令
(33)
将系统(32)转换为
(34)
由于系统(32)和系统(34)有相同的首次积分(35)
(35)
所以两个系统除了奇直线 之外有相同的拓扑相图。因此我们可以通过研究系统(34)的相图达到研究系统(32)的相图的目的。
令
(36)
则有
(37)
4. 分支曲线
令
(38)
(39)
则
(40)
系统(34)变为
(41)
显然,系统(41)的奇点都在 轴或直线 上。由(40)可得
(42)
当 时, 有一个零点
(43)
为 的极小值点。
当 时, 有两个零点 ,其中 为 的极大值点, 为 的极小值点。
令
(44)
(45)
再定义 分支曲线,满足在这条分支曲线上有三个鞍点相连。曲线表达式可由下面方程组解出
(46)
接下来研究在c-g平面上,系统(41)的分支相图。
5. 当n = 2时的分支相图
(47)
(48)
(49)
(50)
(51)
由式子(6)给出, 由式子(7)给出, 由式子(8)给出。具体情况如下:
1) 当 时, ,, 三支曲线交于 , 与 交于 , 与 交于 。
2) 当 时, ,, 三支曲线交于 , 与 交于 , 与 交于 。
3) 当 时, ,, 三支曲线交于 ,, 与 交于 , 与 交于 。
4) 当 时, ,, 三支曲线交于 , 与 交于 ,, 与 交于 。
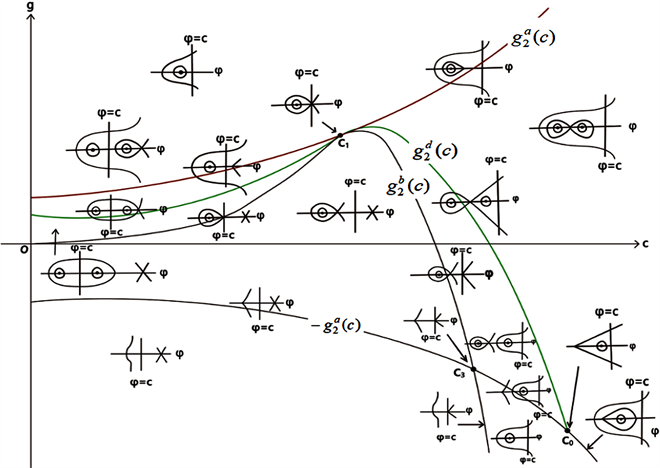
Figure 1. Bifurcation phase portrait of system (41) when ,
图1. 当 , 时,系统(41)的分支相图

Figure 2. Bifurcation phase portrait of system (41) when ,
图2. 当 , 时,系统(41)的分支相图
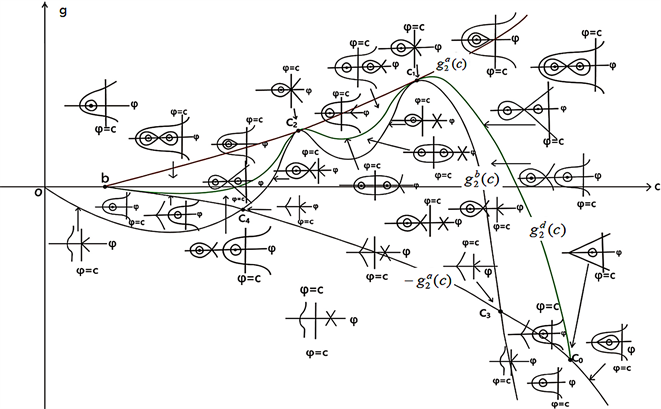
Figure 3. Bifurcation phase portrait of system (41) when ,
图3. 当 , 时,系统(41)的分支相图
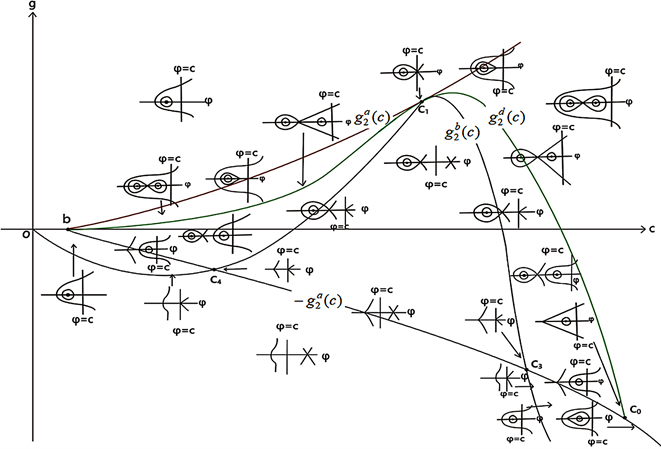
Figure 4. Bifurcation phase portrait of system (41) when ,
图4. 当 , 时,系统(41)的分支相图
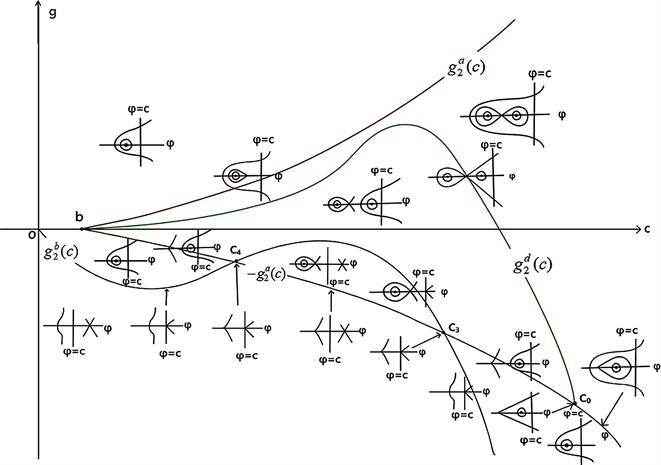
Figure 5. Bifurcation phase portrait of system (41) when ,
图5. 当 , 时,系统(41)的分支相图
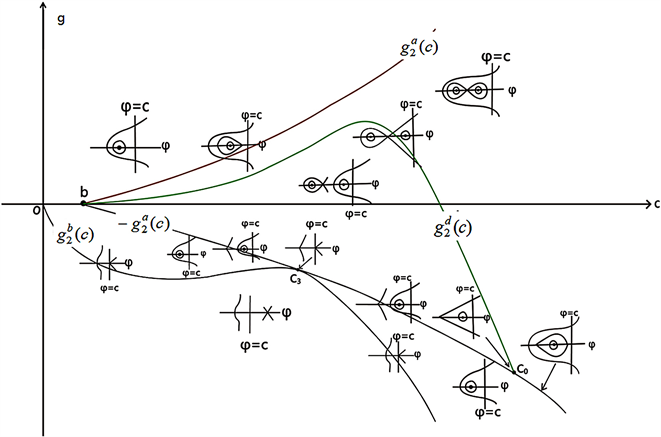
Figure 6. Bifurcation phase portrait of system (41) when ,
图6. 当 , 时,系统(41)的分支相图
5) 当 时, ,, 无交点, 与 交于 ,, 与 交于 。
6) 当 时, ,, 无交点, 与 交于 , 与 交于 。
7) 当 时, ,, 无交点, 与 无交点, 与 交于 。
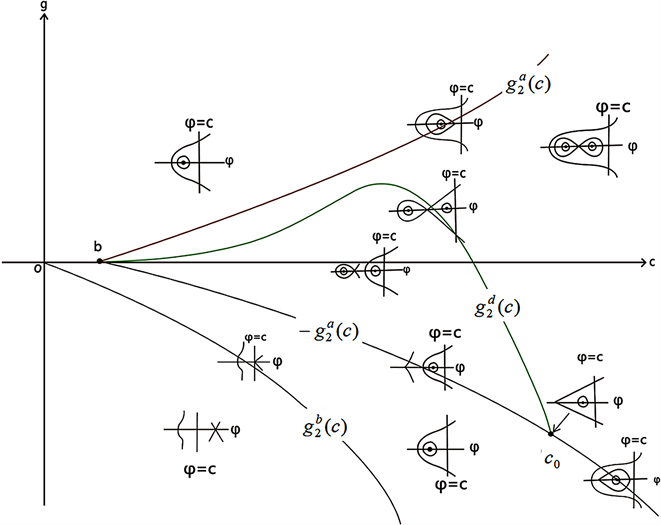
Figure 7. Bifurcation phase portrait of system (41) when ,
图7. 当 , 时,系统(41)的分支相图
6. 当n = 3时的分支相图
(52)
(53)
(54)
其中p,q,l分别由式子(21),(22),(24)给出,图中点 , 为 , 和 三支曲线的交点,由方程(27)决定。具体情况如下:
1) 当 时, , 和 交于 。
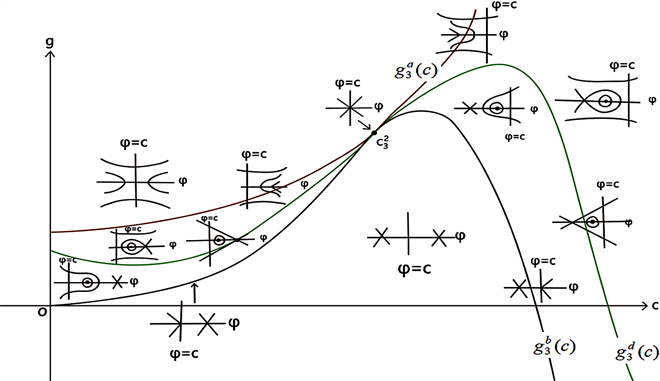
Figure 8. Bifurcation phase portrait of system (41) when ,
图8. 当 , 时,系统(41)的分支相图
2) 当 时, , 和 交于 。
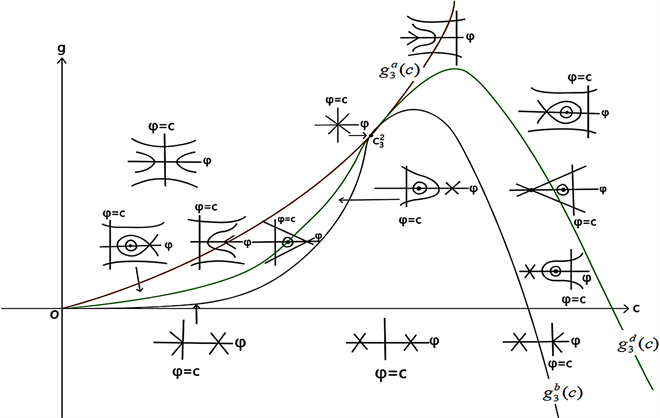
Figure 9. Bifurcation phase portrait of system (41) when ,
图9. 当 , 时,系统(41)的分支相图
3) 当 时, , 和 交于 ,。
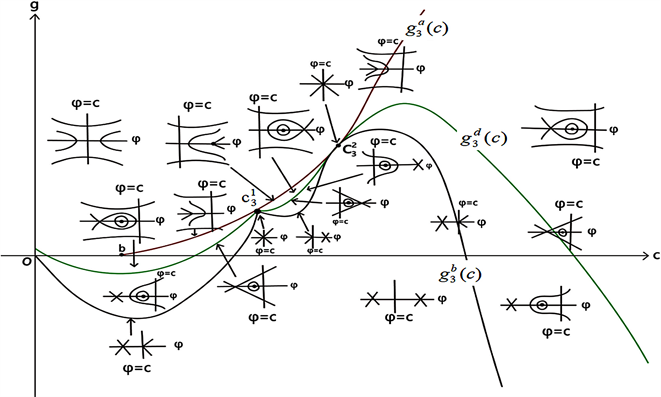
Figure 10. Bifurcation phase portrait of system (41) when ,
图10. 当 , 时,系统(41)的分支相图
4) 当 时, , 和 交于 。

Figure 11. Bifurcation phase portrait of system (41) when ,
图11. 当 , 时,系统(41)的分支相图
5) 当 时, , 和 无交点。
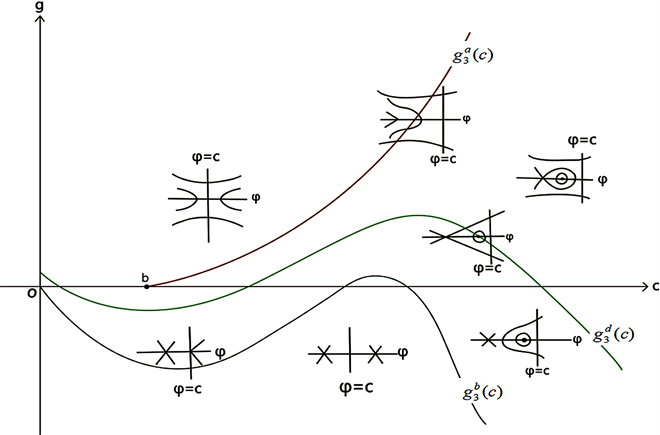
Figure 12. Bifurcation phase portrait of system (41) when ,
图12. 当 , 时,系统(41)的分支相图
7. 解的具体推导
1) 当 , 时,系统(41)的分支相图(见图1~7),三个鞍点相连的相图中奇直线 右侧的轨道有如下表达式
(55)
其中 ,,,k分别由式子(6),(7),(8),(9)给出。
将(31)带入(55)并沿着该轨道积分,得到
(56)
求解方程(56)得到非线性波解 由式子(12)给出。
2) 当 , 时,系统(41)的分支相图(见图1~7)中连接三个鞍点的轨道有如下表达式
(57)
其中 ,,,k分别由式子(6),(7),(8),(9)给出。
将(31)带入(57)并沿着该轨道积分,得到
(58)
求解方程(58)得到非线性波解 由式子(13)给出。
3) 当 时, ,系统(41)的分支相图(见图1~7)中三个鞍点左侧的同宿轨有如下表达式
(59)
其中 ,,,k分别由式子(6),(7),(8),(9)给出。
将(31)带入(59)并沿着该轨道积分,得到
(60)
求解方程(60)得到非线性波解 由式子(14)给出。
4) 当 , 时,系统(41)的分支相图(见图1~7)中连接三个奇点的轨道有如下表达式
(61)
其中 由式子(6)给出。
将(31)带入(61)并沿着该轨道积分,得到
(62)
求解方程(62)得到非线性波解 由式子(15)给出。
5) 当 , 时,系统(41)的分支相图(见图8~12)中连接三个鞍点的轨道有如下表达式
(63)
其中f, ,e分别由式子(19),(20),(23)给出, , 由方程(27)决定。
将(31)带入(63)并沿着该轨道积分,得到
(64)
求解方程(64)得到非线性波解 由式子(26)给出。
基金项目
广东省基础与应用基础研究基金资助(项目编号:2019B151502062)。
文章引用
朱 贇,刘 锐. 广义Fornberg-Whitham方程的某些非线性波解
Some Nonlinear Wave Solutions for the Generalized Fornberg-Whitham Equation[J]. 应用数学进展, 2020, 09(09): 1589-1603. https://doi.org/10.12677/AAM.2020.99187
参考文献
- 1. Liu, Z.R. and Qian, T.F. (2001) Peakons and Their Bifurcation in a Generalized Camassa-Holm Equation. International Journal of Bifurcation and Chaos, 11, 781-792. https://doi.org/10.1142/S0218127401002420
- 2. Song, M., Ahmed, B., Zerrad, E. and Biswas, A. (2013) Domain Wall and Bifurcation Analysis of the Klein-Gordon Zakharov Equation in (1+2)-Dimensions with Power Law Nonlinearity. Chaos, 23, Article ID: 033115. https://doi.org/10.1063/1.4816346
- 3. Pan, C.H., Ling, L.M. and Liu, Z.R. (2014) A New Integrable Equation with Cuspons and Periodic Cuspons. Physica Scripta, 89, Article ID: 105207. https://doi.org/10.1088/0031-8949/89/10/105207
- 4. Pan, C.H. and Liu, Z.R. (2015) Infinitely Many Solitary Waves of an Integrable Equation with Singularity. Nonlinear Dynamics, 83, 1-7. https://doi.org/10.1007/s11071-015-2420-7
- 5. Whitham, G.B. (1967) Variational Methods and Applications to Water Wave. Proceedings of the Royal Society of London. Series A, 299, 6-25. https://doi.org/10.1098/rspa.1967.0119
- 6. Ivanov, R. (2005) On the Integrability of a Class of Nonlinear Dispersive Wave Equations. Journal of Nonlinear Mathematical Physics, 1294, 462-468. https://doi.org/10.2991/jnmp.2005.12.4.2
- 7. Fornberg, B. and Whitham, G.B. (1978) A Numerical and Theoretical Study of Certain Nonlinearwave Phenomena. Philosophical Transactions of the Royal Society A, 289, 373-404. https://doi.org/10.1098/rsta.1978.0064
- 8. Camassa, R. and Holm, D.D. (1993) An Integrable Shallow Water Equation with Peaked Solitons. Physical Review Letters, 71, 1661-1664. https://doi.org/10.1103/PhysRevLett.71.1661
- 9. He, B., Meng, Q. and Li, S. (2010) Explicit Peakon and Solitary Wave Solutions for the Modified Fornberg-Whitham Equation. Applied Mathematics and Computation, 217, 1976-1982. https://doi.org/10.1016/j.amc.2010.06.055
- 10. Liu, Z. and Liang, Y. (2011) The explicit Nonlinear Wave Solutions and Their Bifurcations of the Generalized Camassa-Holm equation. International Journal of Bifurcation and Chaos, 21, 3119-3136. https://doi.org/10.1142/S0218127411030556
- 11. Fan, X., Yang, S., Yin, J., et al. (2010) Bifurcations of Traveling Wave Solutions for a Two-Component Fornberg-Whitham Equation. Communications in Nonlinear Science and Numerical Simulation, 16, 3956-3963. https://doi.org/10.1016/j.cnsns.2011.02.010
- 12. Jiang, B. and Bi, Q. (2010) Smooth and Non-Smooth Traveling Wave Solutions of the Fornberg-Whitham Equation with Linear Dispersion Term. Applied Mathematics and Computation, 216, 2155-2162. https://doi.org/10.1016/j.amc.2010.03.050