 Advances in Geosciences 地球科学前沿, 2012, 2, 138-144 http://dx.doi.org/10.12677/ag.2012.23020 Published Online September 2012 (http://www.hanspub.org/journal/ag.html) Study of Fluid-Flow Effects on Seismic Propagation in Fractured Porous Media* Jiong Liu1,2,3, Xiucheng Wei1,2, T ianshe ng Chen1,2 1Collugue of Geosciences, C hina University of Petroleum (Beijing), Beijing 2Exploration & Production Research Institute, S i no pe c , Beijing 3Sinopec Key Laboratory of M u lt i Componen ts Seismic Technology, Beijing Email: jiong3330@yahoo.com.cn Received: Jun. 8th, 2012; revised: Jun. 28th, 2012; ac c e pted: Jul. 7th, 2012 Abstract: Many researches on seismic propagation in fractured rocks have been done, but almost all centered on frac- ture parameters’ effects on the assumption that the background s are simple elastic solids. In reality the backgrounds are complex porous media where solid rock grain and fluid coexist. Recent experimental researches imply that not only rock structure, but also fluid-flow in porous and fracture space that caused by dynamic stress can affect seismic wave in fractured media. In this paper, the effect of fluid-flow in porous media with aligned fractures is studied. Hudson’s frac- ture theory and Gassmann equation in anisotropic media are adopted to compute seismic velocities. In dry condition, low-frequency fluid-saturation cond ition and high-frequency fluid-saturation cond ition, Seismic velocities are computed. Comparing these results we find that fluid-flow can change seismic velocities in anisotropic fractured porous medium, which make qP wave and qSV wave dispersion, and the dispersion magnitude is related propagation direction. But it nearly has no effect on qSH wave. Keywords: Fracture; Fluid Saturation; Dispersion; Anisotropy; Hudson Theory 流体流动对孔隙裂缝介质中地震波传播影响研究* 刘 炯1,2,3,魏修成 1,2,陈天胜 1,2 1中国石油大学(北京)地球科学学院,北京 2中国石化石油勘探开发研究院,北京 3中国石化多波地震技术重点实验室,北京 Email: jiong3330@yahoo.com.cn 收稿日期:2012 年6月8日;修回日期:2012 年6月28 日;录用日期:2012 年7月7日 摘 要:前人已经对裂缝岩石介质中的地震波传播开展了大量研究。这些研究大多在背景介质为弹性固体的假 设前提下考虑裂缝各种参数对地震速度的影响。然而实际地下裂缝岩石的背景是岩石颗粒和流体并存的孔隙介 质。最近的实验研究表明不仅岩石结构会影响地震波速度,而且由动态应力所引起的孔隙裂缝中的流体流动也 会对地震速度产生显著的影响。本文在含定向排列裂缝的孔隙介质中,研究流体流动对地震波传播的影响。主 要通过 Hudson 理论和各向异性 Gassmann 理论求得干燥、低频流体饱和以及高频流体饱三种情况下的地震波速 度,将它们进行对比发现,流体流动会对裂缝各向异性介质中的地震波产生影响:准纵波(qP)和准 SV(qSV)波发 生明显的速度频散现象,且它们频散的大小和波传播的方向有关;流体流动对准SH(qSH)波影响不大。 关键词:裂缝;流体饱和;频散;各向异性;Hudson 理论 1. 引言 裂缝作为一种复杂的空间结构,大量存在于自然 界的各种地层岩石中。一般裂缝的存在会改变原有岩 石的力学的性质,使得岩石中的地震波传播发生改 *资助信息国家重点自然科学基金(40839901)资助。 Copyright © 2012 Hanspub 138  流体流动对孔隙裂缝介质中地震波传播影响研究 变。另一方面,裂缝又增加了岩石中的各种孔隙的连 通性,使得油、气、水等孔隙流体的流通性大大加强。 所以裂缝介质一直是许多学科的研究热点,如油气地 震勘探开发、地下水的抽取。 前人已经对含微小裂缝介质地震波传播开展了 大量的研究。O’Connell Budiansky[1]利用自洽理论研 究了含裂缝统计各向同性介质的有效弹性模量,并对 不同密度情况下裂缝含水时的地震速度进行了理论 计算。上世纪八十年代,Crampin[2]通过研究发现,地 震波在定向裂缝介质中传播时和波在各向异性介质 中的传播等效,都会出现快横波和慢横波分裂的现 象,并将含定向裂缝的介质称为广泛扩容性各向异性 EDA(extensive dilatancy anisotropy)介质。对于一般岩 石EDA 介质中的众多微小裂缝,Hudson[3,4]将它们看 成是以一个个非常扁的椭球体,然用弹性扰动理论推 导出裂缝等效各向异性介质的弹性系数与各向同性 背景介质的弹性系数、裂缝参数之间的关系,并给出 了裂缝中不同充填物对弹性常数的影响。基于对有椭 球包含物的各向同性固体内部应变的 Eshelby 静态 解,Cheng[5]给出了定向排列裂缝等效横向各向同性介 质的弹性模量。Schoenberg 和Sayers[6]将裂缝看成是 具有线性滑动边界条件的柔性边界,并将裂缝介质的 柔度表示为裂缝背景介质的柔度和每一裂缝柔度之 和,然后根据边界条件推导出了含裂缝等效各向异性 介质的柔度矩阵。随后很多学者运用这些等效介质理 论研究了地震波在统计各向同性裂缝介质以及定向 排列各向异性裂缝介质中的传播特点。在以前的研究 中,人们一般将裂缝简化为均匀各向同性弹性背景介 质中的包体或夹层,然后在线弹性假设前提下研究裂 缝介质中地震波的传播特性。然而实际地下裂缝所处 的岩石介质是多孔介质,而并不是简单弹性固体。裂 缝所处的背景岩石中孔隙空间的大小,孔隙中流体的 种类都会对通过的地震波产生作用。最近实验研究表 明孔隙介质中的流体在外界动态应力的作用下会产 生压力梯度,从而使孔隙流体发生流动,这种流动会 对其间传播的地震波产生较大的影响,使得地震波发 生明显的频散现象[7,8]。前面介绍的裂缝等效介质理论 考虑了裂缝形态及其包含物对介质弹性性质的影响, 但没有考虑到孔隙与裂缝之间、孔隙与孔隙之间以及 裂缝与裂缝之间流体流动的情况,所以这些理论预测 的只是高频近似下的值。 本文主要研究在含定向排列裂缝的孔隙介质中, 流体流动情况对地震波的影响。首先我们用 Hudson 等效介质理论求出干燥情况下含裂缝孔隙介质中的 弹性常数和地震波速度,然后在干裂缝孔隙介质计算 的基础通过各向异性的 Gassmann方程求出流体饱和 时地震低频情况下的裂缝孔隙介质的地震波速。并在 流体不流动的假设前提下运用 Hudson 理论求得高频 时裂缝孔隙介质的波速。最后将干燥、地震低频情况 下流体饱和以及高频情况下流体饱和三种情况下的 地震波速度进行对比,研究流体饱和对地震波传播的 影响。 2. 裂缝等效介质理论和各向异性 Gassmann 方程 本部分从两个方面分别介绍裂缝等效各向异性 介质的 Hudson理论和低频情况各向异性介质的 Gass- mann 理论。 2.1. 裂缝各向异性介质的 Hudson 理论 实际地下众多的定向排列微小裂缝在长波长近 似的前提下可以等效为各向异性介质。本文考虑的是 对称轴垂直分布的裂缝介质,其等效介质刚度矩阵如 下: 11 1213 1211 13 13 33 33 44 44 00 0 00 0 00 0 000 000 0000 CCC CCC CCC C C C 66 C (1) Hudson 基于裂缝为薄币椭球形状的假设前提,根 据弹性固体中的平均波场散射理论得到了裂缝等效 介质刚度矩阵中各弹性常数同裂缝以及背景介质的 关系,其二阶精度的表达式如下[4]: 22 2 113 3 215 2 q CU U (2) 22 333 3 2 2( 15 q CU 2)U (3) 2 44 11 38 2 15 2 CU U (4) Copyright © 2012 Hanspub 139  流体流动对孔隙裂缝介质中地震波传播影响研究 66 C (5) 2 133 3 2 15 q CU U (6) 12 1166 2CC C (7) 其中 、 是各向同性背景介质的拉梅常数; 表示 裂缝密度;参数q可以表示成 2 2 1528 28q (8) 对于不同裂缝的填充状态 ,有着不同的表 达形式,当裂缝干燥状态,表达式如下: 1 U3 U 1 16 2 33 4 U (9) 3 42 3 U (10) 当裂缝含弱包含物时, ,表达式如下: 1 U3 U 1 16 21 334 1 U M (11) 3 421 31 U (12) 其中 M 、可以用弱包含物的体积模量k K 剪切模量 表述成 42 34 M (13) Hudson在推导裂缝等效各向异性弹性参数的过 程中假定裂缝之间是彼此隔离的,裂缝中的流体以及 裂缝与背景孔隙之间的流体不能互相流动,所以各裂 缝中的流体压力是不平衡的。 Hudson 理论得到的是非 常高频情况下饱和裂缝岩石的属性,它适用于实验室 超声条件。而实际地震频率比较低,岩石中裂缝之间 的流体、背景孔隙之间的流体以及裂缝与背景孔隙之 间的流体在一个应力周期内有充分的时间发生流动, 使流体压力达到平衡。所以 Hudson 理论并不适合地 震频段下的含流体裂缝介质。 2.2. 各向异性 Gassmann 理论 人们常常用弹性固体中波来描述地震波在岩石 中的传播。但是实际岩石并不是简单均匀的弹性固 体。岩石中除了固体成分外还有许多大小不一的孔 隙,这些孔隙以及其间包含的流体都会对岩石中的地 震波产生影响。针对宏观均匀、各向同性的情况, Gassmann 建立了岩石干骨架、固体基质、孔隙流体的 体积模量与岩石整体体积模量之间的静态关系,并在 实际的油气勘探中得到了广泛的应用。Brown 和 Korringa[9]利用弹性柔度张量导出了各向异性情况下 的Gassmann 方程。Borris[10]推导了在一种流体饱和情 况下,含定向排列裂缝的孔隙介质中的各向异性 Gassmann 方程,得到的含流体裂缝孔隙介质在静态时 的刚度表达形式如下: sat dry,, 1,2,3,,6 D ijiji j CC bbij (15) dry dry dry 123 ,1,2,3,, 3 iii ii g CCC bi K 6 (16) 其中 、分别表示流体饱和以及干燥情况下各 向异性介质的弹性参数, sat ij Cdry ij C g K 是固体颗粒的体积模量。 参数 、 * D 和 表达式如下: 123 13g Dbb K b (17) 111 fg KK (18) 123 1 (19) 445 0 (20) 其中 是背景孔隙度和裂缝孔隙度的总和, f K 是流 体体积模量。 与各向同性的 Gassmann理论一样,各向异性的 Gassmann 理论也是在流体静态情况下获得的,所以严 格说来它并不适合含定向裂缝孔隙介质中地震波传 播情况。不过由于常规地震勘探中弹性波频率较低, 应用 Gassmann方程可以完全符合一般工程精度要求, 而对于声波测井频段(~104 Hz),和实验室超声测量 (~106 Hz)直接应用各向Gassmann 方程可能会带来较 大误差。 3. 流体饱和 VTI 裂缝介质中地震波的速度 本部分我们以VTI 介质为例,研究含定向排列裂 缝孔隙介质在流体饱和情况下的地震波的速度。 Copyright © 2012 Hanspub 140  流体流动对孔隙裂缝介质中地震波传播影响研究 3.1. 流体饱和裂缝介质中的速度 本部分我们以VTI 介质为例,研究含定向排列裂 缝孔隙介质在流体饱和情况下的地震波的速度。 对于如图1所示对称轴垂直的VTI 裂缝介质,将 流体饱和的刚度矩阵(1)以及平面波表达形式代入弹 性波动方程中,得到准纵波、两个准横波的表达形式 如下[11]: sat2 sat2 sat 11 3344 sat sin cos 2 P CCC V M (21) sat2 sat2 sat 11 3344 sat sin cos 2 SV CCC V M (22) sat 2sat2 66 44 sat sin cos SH CC V (23) 其中 sat 是含流体裂缝介质的密度; 是波传播方向 与纵轴之间的夹角。参数M可以写成如下形式: 2 sat sat2sat sat2 114433 44 2 sat sat 13 44 sin cos sin 2 MCC CC CC (24) 快、慢横波之间的速度差异反映了裂缝介质各向 异性程度,本文用如下横波分裂因子来衡量裂缝介质 中各向异性的强弱[12],并研究流体流动对横波分裂因 子的影响。 22 22 qSH qSV qSH qSV VV sVV (25) 3.2. 流体饱和孔隙裂缝介质中地震波频散研究 本文主要通过计算含裂缝孔隙介质在干燥、低频 含水、高频含水情况下的地震波速度来研究流体对裂 Figure 1. Schematic of seismic propagation in VTI media 图1 . VT I介质中地震波传播示意图 缝孔隙介质 况是指岩石 的Hudson 公 式来研究 情 中地震波速度的影响。干燥情 的裂缝和背景孔隙介质中不含任何流体或只含少量 气体且气体的弹性模量、质量可以忽略。低频是指外 界应力波频率很低,当岩石中含有流体时,裂缝和裂 缝之间,背景孔隙介质之间以及裂缝和背景孔隙介质 之间的流体会发生充分流动,使得所有孔隙流体压力 达到平衡。一般地震频段属于低频。而高频是指外界 应力波频率很高,当裂缝介质中含有流体时,裂缝与 裂缝之间,背景孔隙之间以及裂缝与背景孔隙之间虽 然有压力差,但没有时间发生流体流动。实验室的超 声岩石物理测量属于高频的范畴。 在干燥情况下,我们可以采用干燥 裂缝孔隙介质中的地震波速度。在流体饱和 高频情况下,可以用含弱包含物的Hudson 公式来理 论预测地震速度,只是对应的背景弹性模量用含流体 孔隙介质的 Biot 高频弹性模量来代替,具体公式参见 附录 A。对于流体饱和的低频情况,由于 Hudson 公 式没有考虑到介质中裂缝与背景孔隙岩石中的流体 流动,所以它并不适合。这个时候我们首先用Hudson 公式求出干燥时候的裂缝孔隙介质骨架的弹性参数, 然后通过各向异性的 Gassmann 理论求解低频时裂缝 孔隙内流体充分流动 况下的地震波速度。 假设 VTI 裂缝介质中固体颗粒的体积模量为 70 g a K GP ,密度是 3 2870 kgm ;裂缝背景孔 般等径孔隙 g 度隙介质的一 0.08 P ,裂缝孔隙度 0.02 f ,裂 缝密 度0.08 f ;当裂缝闭合时,干燥 况下的纵波孔隙背景情 dry 00 ms,横波 _40 bp V dry m s。本文考虑在 低频三 ,其中水的密度 _1700 bp V 种情况下的地 干燥和含水高、 震波速度 3 1000 kgm 。 f 图2是计算得到的裂缝孔隙介质中准纵波(qP)不 同传 (qSV)的速度。可以看到低频流体 饱和 播方向的速度。 qP 波速度沿裂缝面,即 90 对 称。相对于干燥的情况,流体的存在会使裂缝介质中 的qP 波速度升高。流体不流动的高频qP波速度要比 流体充分流动时的低频速度高,这种差异在 qP 波沿 称轴传播时最大,并随着波传播方向同对称轴之间夹 角的增大而减小,当 qP 波沿裂缝面传播时qP 波高低 频速度基本一致。 图3是准 SV波 情况下的qSV 波速度要比干燥时候的低,这主要 Copyright © 2012 Hanspub 141 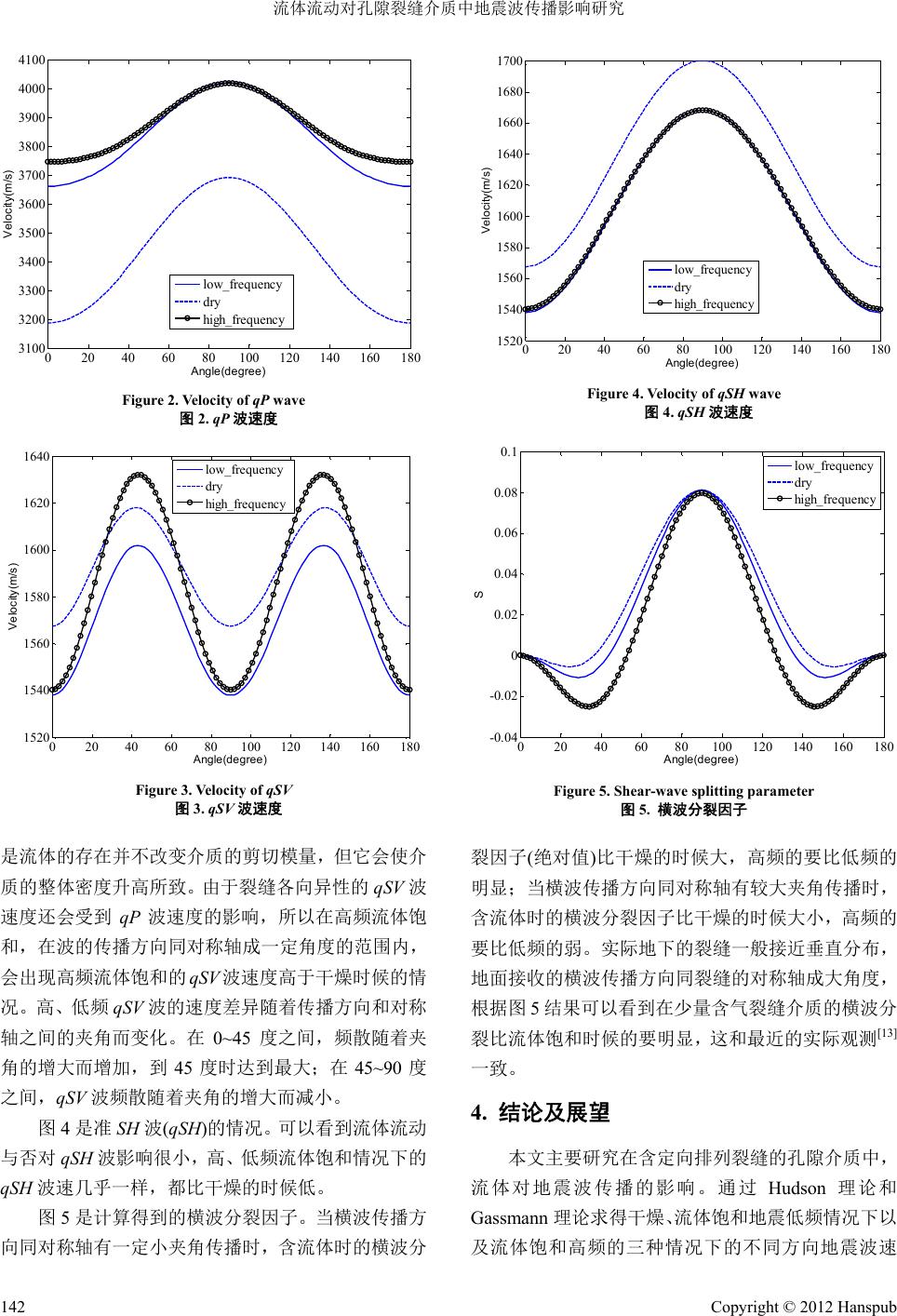 流体流动对孔隙裂缝介质中地震波传播影响研究 020406080100 120 140 160180 3100 3200 3300 3400 3500 3600 3700 3800 3900 4000 4100 An g le ( de g ree ) Velocity(m/s) low_frequ ency dry high_frequency Figure 2. Velocity of qP wave 图2. qP 波速度 020 40 60 80100 120 140160 180 1520 1540 1560 1580 1600 1620 1640 Angle(degree) Velo city(m /s) low_frequency dry high_frequency Figure 3. Velocity of qSV 是流体的存在并不改变介质的剪切模量,但它会使介 体流动 与否 波传播方 向同 图3. qSV 波速度 质的整体密度升高所致。由于裂缝各向异性的qSV 波 速度还会受到 qP 波速度的影响,所以在高频流体饱 和,在波的传播方向同对称轴成一定角度的范围内, 会出现高频流体饱和的qSV波速度高于干燥时候的情 况。高、低频qSV 波的速度差异随着传播方向和对称 轴之间的夹角而变化。在0~45 度之间,频散随着夹 角的增大而增加,到 45 度时达到最大;在45~90 度 之间,qSV 波频散随着夹角的增大而减小。 图4是准 SH 波(qSH)的情况。可以看到流 对qSH 波影响很小,高、低频流体饱和情况下的 qSH 波速几乎一样,都比干燥的时候低。 图5是计算得到的横波分裂因子。当横 对称轴有一定小夹角传播时,含流体时的横波分 020 40 60 80100120 140 160 180 1520 1540 1560 1580 1600 1620 1640 1660 1680 1700 Angle(degree) Velocity(m/s) low_frequency dry high_frequency Figure 4. Velocity of qSH wave 图4. qSH 波速度 02040 60 80 100 120 140 160 180 -0. 04 -0. 02 0 0.02 0.04 0.06 0.08 0.1 Angle(degree) S low_frequency dry high_frequency Figure 5. She ar-wave splitting parameter 裂因子(绝对值)比干燥的时候大,高频的要比低频的 在含定向排列裂缝的孔隙介质中, 流体 图5. 横波分裂因子 明显;当横波传播方向同对称轴有较大夹角传播时, 含流体时的横波分裂因子比干燥的时候大小,高频的 要比低频的弱。实际地下的裂缝一般接近垂直分布, 地面接收的横波传播方向同裂缝的对称轴成大角度, 根据图 5结果可以看到在少量含气裂缝介质的横波分 裂比流体饱和时候的要明显,这和最近的实际观测[13] 一致。 4. 结论及展望 本文主要研究 对地震波传播的影响。通过 Hudson 理论和 Gassmann 理论求得干燥、流体饱和地震低频情况下以 及流体饱和高频的三种情况下的不同方向地震波速 Copyright © 2012 Hanspub 142  流体流动对孔隙裂缝介质中地震波传播影响研究 Copyright © 2012 Hanspub 143 质中 地震 响很小。 况下 考虑了高、低频两种极限情况下,流体饱和 裂缝 参考文献 (References) Seismic velocities in dry and waves in nsversely anisotropic me- y of d attenuation in Nur. Dispersion analysis of acoustic velocities in rringa. On the dependence of the elastic proper- saturated porous rocks with vko, T. Mukerji and J. Dvorkin. The rock physics hand- ersion and anisotropy tion of elastic waves in a fluid- n a fluid- the con- 度以及横波分裂因子,将它们进行对比发现: 1) 孔隙中的流体流动会对裂缝各向异性介 波速度产生影响,使得准纵波和准 SV 速度发生 改变,改变的大小和波传播方向相关。 2) 孔隙流体流动对准 SH 波的速度影 Ber 3) 在地震波传播方向和裂缝法线成大角度的情 ,孔隙之中流体的存在会使介质的各向异性程度 减弱。 本文 孔隙介质中地震波传播速度,所得结果有助于将 实验室高频速度外推至地震频段。此外还有许多时候 需要了解中间频段地震波速度,如声波测井情况下裂 缝孔隙介质中的地震速度,这些将是我们下一步的研 究内 [1] R. J. O’Connell, B. Budiansky. saturated cracked solids. Journal of Geophysical Research, 1974, 79: 5412-5426. [2] S. Crapmpin. Effective anisotropic elastic constants for wave propagation through cracked solids. Geophysical Journal of the Royal Astronomical, 1984, 76(1): 135-145. [3] J. A. Hudson. Overall properties of a cracked solid. Mathemati- cal Proceeding of the Cambridge, 1980, 88: 371-384. [4] J. A. Hudson. Wave speeds and attenuation of elastic material containing cracks. Geophysical Journal of the Royal Astronomical, 1981, 64(1): 133-150. [5] C. H. Cheng. Crack models for a tra dium. Journal of Geophysical Research, 1993, 98: 675-684. [6] M. Schoenberg, C. M. Sayers. Seismic anisotropy anisotrop fractured rock. Geophysics, 1995, 60: 204-211. [7] K. W. W i nkler. Dispersion analysis of velocity an ea sandstone. Journal of Geophysical Research, 1985, 90: 6793-6800. [8] Z. Wang, A. rocks. The Journal of the Acoustical Society of America, 1990, 87: 2384-2395. [9] R. Brown, J. Ko ties of a porous rock on the compressibility of the pore fluid. Geophysics, 1975, 40(3): 608-616. [10] B. Gurevich. Elastic properties of aligned fractures. Journal of Applied Geophysics, 2003, 54: 203- 218. [11] G. Ma book. Cambridge University Press, 2003. [12] R. J. Galvin. Elastic wave attenuation, disp in fractured porous media. Curtin University of Technology, 2007. [13] C. M. Van Der Kolk, W. S. Guest and J. H. H. M. Potters. The 3D shear experiment over the Natih field in Oman: The effect of fracture-filling fluids on shear propagation. Geophysical Pros- pecting, 2001, 49(2): 179-197. [14] M. A. Biot. Theory of propaga saturated porous solid: I. Low-frequency range. Journal of the Acoustical Society of America, 1956, 28(2): 168-178. [15] M. A. Biot. Theory of propagation of elastic waves i saturated porous solid: II. Higher frequency range. Journal of the Acoustical Society of America, 1956, 28(2): 179-191. [16] D. L. Johnson, T. J. Plona. Acoustic slow waves and solidation transition. The Journal of the Acoustical Society of America, 1982, 72: 556-565.  流体流动对孔隙裂缝介质中地震波传播影响研究 附录 A 1956 年,Biot[14,15]从拉格朗日方程出发,同时引 入广义坐标的概念,首次建立了各向同性孔隙中弹性 波传播的理论,奠定了孔隙介质中波传播的理论基 础。Biot理论建立的地震波速度同孔隙流体、矿物骨 架的关系,并预测了地震速度同地震频率的关系。 Johnson和Plona[16]推导了 Biot理论中高频极限情况下 的纵波速度,其结果如下: 22 11 2212 2 11 2212 4 2 P BB PRQ V 2 (A1) 其中 11 、22 、12 表示孔隙介质中的密度,它们同 固体矿物质密度、孔隙度、孔隙流体密度、孔隙曲 折度有关[14]。参数 B、P 、 R 、 Q可以表示成如下形 式: 22 1112 2BPRQ (A2) 11 4 13 mgggmf m mgg f KKK KKK PKK KK (A3) 1 1 mg g mgg f KK K Q K KKK (A4) 2 1 g mgg f K R K KKK (A5) 其中 g K 、m K 、 f K 分别表示固体矿物颗粒,固体骨 架,孔隙流体的体积模量; m 是固体骨架的剪切模 量; 是孔隙度。 在已知固体骨架弹性模量的基础上,通过(A1)~ (A5)可以求得孔隙介质中纵波的高频极限速度,再利 用如下关系可以求得孔隙介质高频极限的弹性模量。 2 2P V (A6) m (A7) 其中 是孔隙介质的总密度, 它和固体颗粒密度 g , 孔隙流体密度 f 关系如下: 1 g f (A8) Copyright © 2012 Hanspub 144 |