 Transmission and Distribution Engineering and Technology 输配电工程与技术, 2012, 1, 1-6 http://dx.doi.org/10.12677/tdet.2012.11001 Published Online September 2012 (http://www.hanspub.org/journal/tdet.html) Calculation on the Key Parameters of the Magnetic Valve Controllable Reactor Meng W ang, Guodong Fan School of Electrical Engineering, Shandong University, Jinan Email: 15966612848@139.com Receiv ed: Aug . 20th, 2012; revised: Aug. 29th, 2012; accepted: Sep. 3rd, 2012 Abstract: Magnetic controlled reactor because of its unique advantages for reactive power compensation has been more and more applications, the principle is the smooth adjustment by changing the effective permeability of the small sec- tion of the reactor, so the design of the small section has an important effect on the operating performance of the mag- netic controlled reactor. Through the operating principle of the reactor and the process state, calculate the magnetic con- trolled reactor key parameters by an equivalent magnetic circuit, and procedures for the preparation and interface using Matlab Gui, finally verify the design results by the MagNet simulation. Keywords: Magnetic Value; Calculate; Simulation 关于磁控电抗器磁阀重点参数的计算 王 梦,范国栋 山东大学电气工程学院,济南 Email: 15966612848@139.com 收稿日期:2012 年8月20 日;修回日期:2012 年8月29 日;录用日期:2012 年9月3日 摘 要:磁控电抗器因其独特的优点在电力系统无功补偿等方面得到了越来越多的应用,其原理是通过改变磁 阀小截面处等效磁导率来平滑调节电抗,因此磁阀的设计对磁控电抗器的运行性能就有着重要的影响。本文从 电抗器运行原理及过程状态出发,通过等效磁路对磁控电抗器磁阀重点参数进行了计算,并使用 Matlab Gui实 现程序的编写和界面的实现,最后针对设计结果进行 Ansoft 仿真,进一步验证了设计的正确性。 关键词:磁阀;计算;仿真 1. 引言 近年来,磁控电抗器在电力系统中已得到越来越 多的重视与应用,其交流绕组和直流绕组合二为一, 简化了结构,也减小了损耗,在运行过程中,铁芯柱 截面一直处于不饱和状态,磁阀处小截面出现饱和, 从而改变铁芯磁导率,进而改变了电抗值,实现了工 作电流的平滑调节[1],在磁控电抗器的设计中,磁阀 的设计(磁阀面积、高度)是重中之重,因为磁阀的参 数直接影响着磁控电抗器谐波含量等重要技术指标。 2. 基本结构 图1为单相四柱式磁控电抗器的结构示意图。 图1中,铁芯柱大截面和磁阀处截面面积分别为 ,磁阀高度 ,工作电压 , dx SS lcos m uE t t ,单边绕 组总匝数 ,磁阀处铁芯面积 N A ,气隙面积 a A 。 3. 等效磁路分析 对于磁控电抗器来说,在容量的整个调节范围内 大截面处于不饱和状态,磁阻很小,磁压降主要集中 Copyright © 2012 Hanspub 1  关于磁控电抗器磁阀重点参数的计算 K 1 K 2 D 铁心 铁心 Figure 1. Structure of magnetic valve controllable reactor 图1. 磁控电抗器结构示意图 在磁阀段,故可以忽略不计,在分析磁阀处等效磁路 的时候,将铁芯的磁化曲线等效为斜率不等的两段[2], 如图 2所示, s B 1 H 为硅钢片饱和磁感应强度,在这取 , 2T1s B ,超过饱和点后斜率为空气磁导率0 。 将其用函数表达式表示出来为: 01 1 01 ss s s s ss s BB BBB B H HBBBB BB BBB (1) 将磁阀处的铁芯和气隙组成的磁路等效为一段 面积为 ,高度为 由某种材料制成的导磁路径。根 据磁通连续性原则: d S l dtta BSB ABA a t (2) 磁阀段铁芯磁特性应满足式(1): t H HB (3) 气隙磁特性满足: 0 a a B H (4) 同时气隙和铁芯磁势相等: ta H H (5) 联立得(1)(2)(3)(4)(5)得 H B s B 1 H s B Figure 2. Magnetic characteristic curve 图2. 磁特性曲线的分段线性模型 01 1 01 BB BBB B H HBBBB BB BBB (6) 其中: 10 10 1111 1 ta ta dd AA AA BBHH SS ,, 可以看出,等效后的磁化曲线仍为两段斜线,磁饱和 点变为原来的 1 1 ta d AA S0 倍,因此改变小截面与大截 面面积的比值就可以改变磁饱和点;饱和点的磁场强 度和超过饱和点的磁导率均不变[3]。 因此,磁控电抗器在不同饱和度下的基波和谐波 电流值为[1]: 1 0 21 0 sin sin 1 sin 21 1 1, 2, 3 n lB IN n lB n INn nn n (7) 其中 为饱和度。 可见磁阀的面积和高度对电抗器的工作电流、调 节深度、谐波水平等技术指标有着直接的影响。 4. 磁阀参数计算 4.1. 铁芯柱面积[4] 铁芯直径按照公式: Copyright © 2012 Hanspub 2  关于磁控电抗器磁阀重点参数的计算 4,mm N DkP (8) 其中 N P:电抗器每柱容量,单位 ,对于单相电 抗器, KVA 2 N N S P;k:经验系数,取 60~70。 所以,铁芯柱面积: 22 20 ,cm d SD (9) 4.2. 绕组匝数 在零励磁条件下,铁芯柱中磁通 只含有交流磁 通[5],由电抗器的数学模型得: m E N (10) 由于 1d BS , 为铁芯柱工作磁感应强度,所以: 1 B 1d BS m E N 。 整理得: 1 m d E NBS (11) 1 B的取值决定于硅钢片的型号和电抗器的性能, 需综合考虑决定。 4.3. 磁阀面积 饱和度 为: 0 2arccos s m BB B , 设0 s m BB KB (12) 0 B为直流磁通密度, 为工作磁通的基频分量。 m B 磁阀面积开的过大,会导致磁阀处出现饱和的同 时铁芯柱也有一定程度的饱和,同时谐波电流大,这 样磁阀的存在就没有意义,所以在电抗器整个容量调 节范围内,铁芯柱要求处于不饱和状态(0 ),即: 01 ds dmd BB KB [6] ,在电抗器的磁阀处需满足 0 0 xs xmx BB KB 1 ,对应的磁阀饱和度 在0到2 范围内,因为只有在这个范围内,电抗器的电抗值是 可调的。 式中 、 0d B0 x B md B mx B 分别为铁芯柱和磁阀处磁感应强度 的直流分量, 、分别为其交流分量,同时从 经济角度考虑, 在设计时取值应当在低于饱和值 的条件下尽可能大些,一般取1.8 T~2.0 T。 mx B 根据磁通连续原则: (13) 得: [5] mdd mxx BS BS 00 dd xx BS BS, 1 sd xd mx x BS KK BS (14) 电抗器铁芯的额定饱和度一般选在 ~2 n 之 间,在这个范围内谐波性能较好且 n ,而 越低 抗 器瞬间过负荷能力就越强。当直流偏磁 大时,电抗 器容量就最大,电抗器运行在额定状态, , ,电 最 x d K K则同 时达到最大值,所以当 n 选定时 cos1 1 2 dn xs mx B SB S (15) 在铁芯柱截面积、 确定前提下,磁阀面积就可以 4.4. 磁阀高度 当磁阀面积确定后,等效磁阀处的 mx B 根据式(15)得出。 B 就可以确 定,当电抗器运行在额定饱和度下,工作 流最大, 为额定工作电流 电 N I ,而 N I 在设计时已知,由式(7)得: 10 sin nn lB N I N I (16) 整理得: 0 sin N nn IN lB (17) 由此便可以求出磁阀高度。 5. 设计软件编写 利用 Matlab Gu将上述计算过程编写 M文件用 户程 技术参数如下: ; i 序,生成用户界面(见图3)。 设计一个10 KV电抗器,主要 额定电压: V; 10 K 额定容量:500A ; KV 额定频率:50 Hz 额定饱和度: 2 。 果如图 4。 ,绕组匝数为 1178 2, 输入相应参数,得到结 图4中,当额定饱和度选择在 2时 匝,铁芯柱大截面面积 424 cm磁阀面积在146 cm2,磁阀高度 54 mm,此外基波、3、5、7次谐波的 最大值也已随磁阀额定饱和度的不同而自动标出,谐 波水平项是指额定工作点下的谐波水平,从图 4中也 Copyright © 2012 Hanspub 3 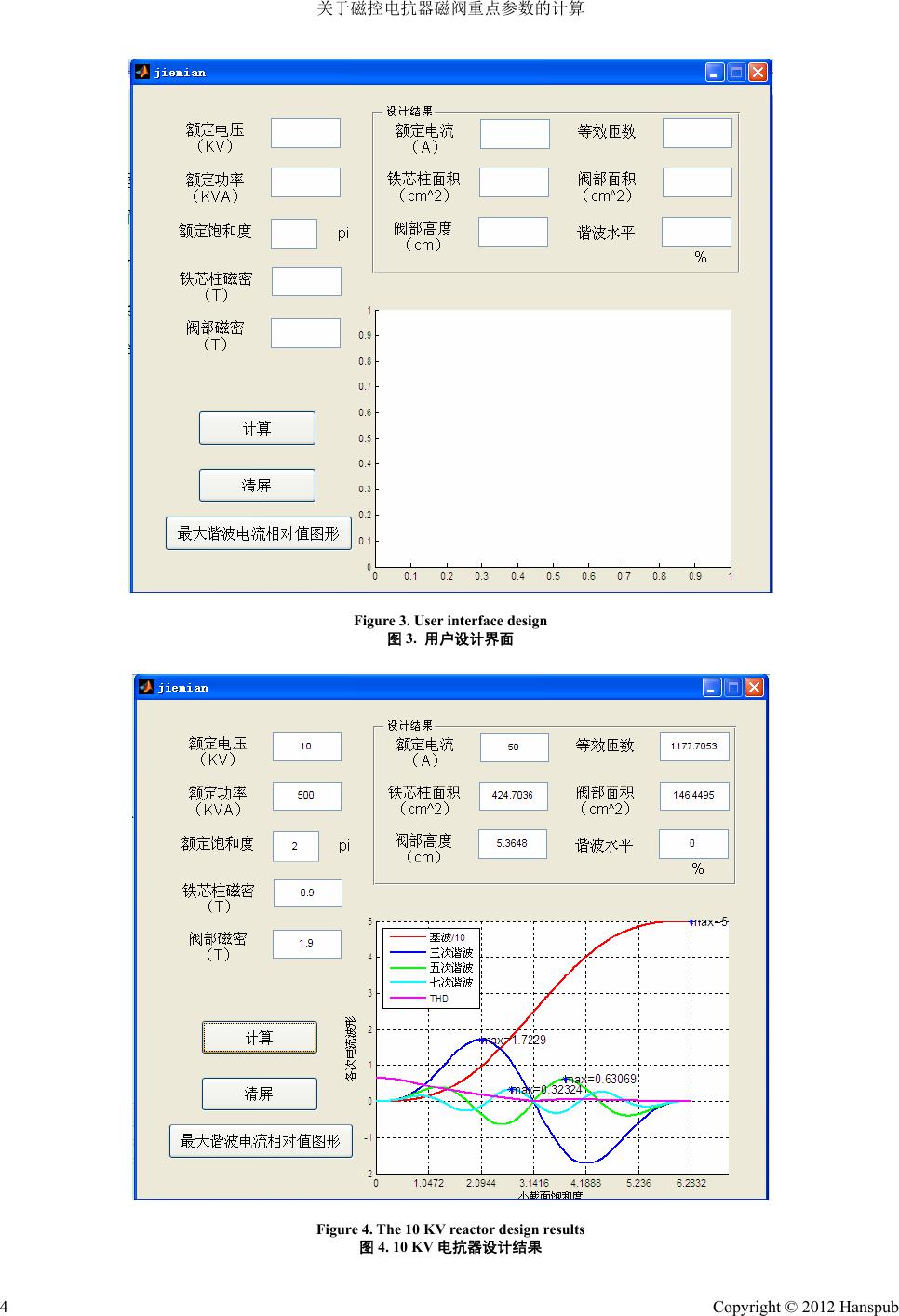 关于磁控电抗器磁阀重点参数的计算 Copyright © 2012 Hanspub 4 Figure 3. User interface design 图3. 用户设计界面 Figure 4. The 10 KV reactor design results 图4. 10 KV电抗器设计结果  关于磁控电抗器磁阀重点参数的计算 可以看出,额定饱和度在 内,谐波水平是比较 低的。 6. 仿真验证 利用设计界面,设计 220 V,600 VA实验型单相 四柱式电抗器,阀面积 7.92 cm2,阀高度 0.6 cm,铁 心面积 23.75 cm2,绕组匝数 520 匝[7](图5和图 6)。 在MagNet 中搭建模型,为方便仿真,采用交流 绕组和直流控制绕组分开控制的方式[8],共有 4个交 流绕组和 4个直流绕组,根据磁控电抗器原理,直流 绕组匝数也应为 520 匝,控制绕组采用直流电压源激 励[9]。以下电流波形为单个交流绕组电流,电抗器的 工作电流是其 2倍关系。 由图 7可以看出当无直流励磁时,铁芯处于不饱 和阶段,工作电流很小,电流波形稍有畸变。 图8可以看出含量比较大的是3次谐波使电流波 形成尖顶波形状,这也与理论分析相一致。从图 9看 出,随着直流激磁电压的增大,波形的谐波成分在减 小,波形质量变好。 图10中可以看出当直流控制电压为 20V 时 定后工作电流基本为正弦电流,说明这时候磁阀处在 工频周期内基本都处于饱和状态,谐波含量很小,这 与设计结果一致,同时也与理论分析完全一致,同时 比较以下情况下的电流波形,也可以侧面得到增大直 流激磁可以提高电抗器的响应速度。 ~2 ,稳 Figure 5. Core structure of HV small MCR 图5. 铁芯结构图 Figure 6. Core dimensions 图6. 铁芯尺寸 Figure 7. (Uk = 0) current waveform 图7. 无直流励磁时(Uk = 0)电流波形及谐波分析 (a) 工作电流波形 (b) 稳定后电流放大波形 Figure 8. Uk = 5tion waveform 图析 V current waveform and current amplifica 8. Uk = 5 V电流波形及谐波分 Copyright © 2012 Hanspub 5  关于磁控电抗器磁阀重点参数的计算 Figure 9. Uk = 10 图9. Uk = 10 V current waveform V电流波形 (a) 工作电流波形 (b) 稳定后电流放大波形 V current waveform 20 V电流波形 7. 结论 本文通过对磁控电抗器等效磁路和工作状态分 析,得出了磁阀关键参数(面积、高度)的理论计算依 据,并以此进行了设计界面的编写,设计界面的实现 可以代替人工计算,同时对设计的正确性进行了 MagNet 仿真,结果与理论分析一致,与设计结果一 致。 参考文献 (References) [1] 陈柏超. 新型可控饱和电抗器理论及应用[M]. 武汉: 武汉水 利大学出版社, 1999. [2] 孔宁. 基于 MCR 的特高压交流输电系统的无功电压控制[D]. 华北电力大学, 2011. [3] 田翠华, 陈柏超. 低谐波双级饱和磁控电抗器研究[J]. 电工 技术学报, 2006, 1(21): 19-23. [4] 刘言菊, 田铭兴. 单相磁阀式可控电抗器的计算机软件设计 [J]. 变压器, 2011, 48(12): 14-16. [5] 吴茜. 自励磁磁 阀式消弧 线圈的设计[D]. 上海交通大学, 2011. [6] 吴茜, 蔡旭, 徐波. 具有两级磁阀的消弧线圈关键参数设计 [J]. 电工技术学报, 2011, 26(10): 224-230. [7] 7李海洋, 赵国生. 三相磁阀式可控电抗器的研究[J]. 变压器, 2011, 48(7): 30-33. [8] 刘仁. 三相磁阀式可控电抗器的研究[D]. 郑州大学, 2010. S. Zhang and G. Z. Chen. A novel continuously tic-valve controllable reactor and its modeling. 2012 IEEE 7th International Power Electronics and Motion Con- trol Conference, 2012: 77-80. Figure 10. Uk = 20 图10. Uk = [9] Y. F. Wang, adjustable magne Copyright © 2012 Hanspub 6 |