Finance
Vol.07 No.03(2017), Article ID:21377,18
pages
10.12677/FIN.2017.73015
An Empirical Analysis on the Dynamic Conditional Correlations between the Both Return Indices of Shanghai Stock Exchange and Shenzhen Stock Exchange
Kejia Yan
Department of Accounting, Finance and Economics, Griffith Business School, Griffith University, Brisbane, Australia

Received: Jun. 29th, 2017; accepted: Jul. 14th, 2017; published: Jul. 17th, 2017

ABSTRACT
Based on the Shanghai Composite Index of Shanghai Stock Exchange and Shenzhen Component Index of Shenzhen Stock Exchange, this paper has calculated the compositional return indices of the both stock markets. The empirical analysis has found that between the both compositional return indices, there are long run and short run cointegration relations, long run and short run bidirectional Granger causality relations, higher dynamic conditional correlation (DCC), higher Clayton lower tail dependence, and higher Gumbel upper tail dependence.
Keywords:Stationary, Cointegration, Causality, Dynamic Correlation, Tail Dependence
对沪深收益指数之间动态条件相关性的实证分析
阎可佳
格里菲斯大学商学院会计、金融与经济系,澳大利亚,布里斯班
收稿日期:2017年6月29日;录用日期:2017年7月14日;发布日期:2017年7月17日

摘 要
基于上海证券交易市场上证综指和深圳证券交易市场深圳成分指数,本文计算了两市的收益指数。实证分析发现,在上证综指收益指数与深证成指收益指数之间,存在长期和短期协整关系、长期和短期双向Granger因果关系、高度动态条件相关关系、高度Clayton下尾依赖关系、以及高度Gumbel上尾依赖关系。
关键词 :平稳关系,协整关系,因果关系,动态相关,尾部依赖

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
长期以来,对于我国沪深两市股票价格收益指数之间相关性的研究,吸引了许多学者的注意力,并且已经取得了不少有益的结论。
第一,许多学者认为沪深两市的收益率之间存在很强的相关性。董彬彬(2010) [1] 研究证明,上证综指和深证成指之间具有高度的相关性。刘喜波、王增、谷艳华(2015) [2] 研究表明,沪深股市日收益率序列之间呈现出很高的相关性,表现为当沪深两市出现大幅震荡时,两市收益率的协同作用就会大幅增强。陈梦龙(2016) [3] 研究表明,沪深两市收益率之间存在较高的正向动态条件相关关系,且具有较强的持续性和平稳性。卢俊香、武宇、杜艳丽(2016) [4] 研究发现,沪深股市日收益率序列呈现出较强的相关性以及对称的尾部相关性,当沪深两市出现大幅震荡时,两市收益率的协同作用将大幅增强。
第二,许多学者认为沪深两市的收益率之间存在很强的尾部相关性。余平、钟波(2007) [5] 研究发现,上证综指和深圳成指之间所存在的尾部相关性主要表现在它们之间具有较强的Clayton Copula下尾关系。类似地,闫海梅、王波(2010) [6] 研究也认为,沪深两市股票指数之间的Clayton Copula下尾相关性很显著;毕付宽(2015) [7] 的研究也表明沪深两市在下跌时相关系数更大。吴鑫育、李心丹(2017) [8] 的研究结果表明,沪深股市交易量和价格两个变量的尾部相关性都具有明显的Clayton Copula下尾非对称特征。
第三,尽管不少学者认为中国沪深两市收益率之间存在很强的相关性和尾部依赖性,但是其长期关系并不具有协整性。吴栩、宋光辉、董艳(2014) [9] 通过对沪深股市夏普比率进行研究发现,沪深股票市场间的协整性不明显,其相关性呈现多重分形波动特征。
对于沪深股票市场价格收益指数之间的相关性问题,以上研究虽然已经得出了一些有益的结论,但是,也存在不少问题。
第一,虽然这些研究都证明上证综指与深证成指收益率之间具有较强的相关关系,但却都没有从因果关系的角度解释二者之间互相影响的方向性,对于两个市场如何互相影响缺乏逻辑解释,所以,本文将研究它们之间的双向因果关系。
第二,两个时间序列之间的依赖关系不仅可能存在长期关系,而且也可能存在短期关系,多数研究对于长期关系关注较多,却对于短期关系研究较少,所以,本文将从长期和短期两个方面研究沪深股市收益率指数之间的协整关系和因果关系。
第三,多数有关沪深两市股票收益率之间关系的研究,都集中在对于它们之间静态关系的研究,而对于动态关系的研究较少,所以,本文也将研究它们之间的动态相关性。
第四,以上对于沪深股市收益率尾部之间依赖关系的研究,基本都认为沪深股市收益率之间存在显著的Clayton Copula下尾依赖,但不存在显著的Gumbel Copula上尾依赖,本文将深入分析沪深股市收益指数之间的下尾、上尾依赖关系。
总之,本文将从长期和短期因果关系、长期和短期协整关系、动态相关关系、尾部依赖关系等方面,综合考察沪深两市股票收益指数之间的相关性,从而得出较为全面的判断。
2. 数据
本文所引用的样本数据,包括上证综指和深证成指日收盘价格指数,均下载自万得数据库,数据库中的数据由中证指数提供。样本数据时间区间以日为单位,介于2002年1月4日至2017年4月10日之间,样本总数共3699个。由于沪、深两市的营业日基本一致,所以,样本数据日期以日历日期为准,不包括节假日。所有运算均通过Eviews 8.0统计软件进行。
因为有两个股票指数,所以,用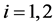 来表示两个股票指数的不同代码。假设
来表示两个股票指数的不同代码。假设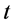 是时间变量,离散型时间变量表示为
是时间变量,离散型时间变量表示为 ,连续型时间变量表示为
,连续型时间变量表示为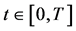 ,二者具有同样的意义,今后将不加区别。
,二者具有同样的意义,今后将不加区别。
假设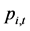 表示第
表示第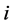 个股票价格指数,
个股票价格指数,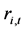 表示从第
表示从第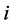 个股票价格指数计算的股票收益指数,它也可以代表股票收益率,今后将不加区别,定义为:
个股票价格指数计算的股票收益指数,它也可以代表股票收益率,今后将不加区别,定义为:
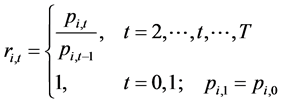 (1)
(1)
显然,股票收益指数 将围绕曲线
将围绕曲线 上下波动。如果
上下波动。如果 ,
, ,则股票
,则股票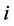 的价格上涨;如果
的价格上涨;如果 ,
, ,则股票
,则股票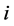 的价格下跌;如果
的价格下跌;如果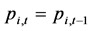 ,
, ,则股票
,则股票 的价格不变。表1列出了本文所要引用到的有关变量,这些变量将在本文中被反复用到。
的价格不变。表1列出了本文所要引用到的有关变量,这些变量将在本文中被反复用到。
3. 模型
3.1. Jarque-Bera正态性检验
Jarque-Bera正态性检验(Jorion, 2007 [10] ; Alexander, 2008 [11] )是为正态分布而设计的一种统计检验方法。假设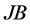 表示样本序列
表示样本序列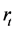 的Jarque-Bera统计量,那么,对于大样本,在零假设为正态分布条件下,统计量
的Jarque-Bera统计量,那么,对于大样本,在零假设为正态分布条件下,统计量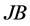 将收敛于一个自由度为2的卡方分布:
将收敛于一个自由度为2的卡方分布:
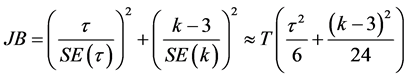 ,
, (2)
(2)
Table 1. Variable definitions for Shanghai Composite Index, Shenzhen Component Index, return indices, residuals of AR models, dynamic conditional variances and standard residuals of GARCH models
表1. 上证综指和深证成指股票价格指数、收益指数、以及AR自回归模型的误差项、GARCH异方差项、标准误差项变量定义
备注: 1) 上证综指市场代码为SH000001,深证成指市场代码为SZ399001;2) 表示上证综指,
表示上证综指, 表示深证成指。
表示深证成指。
这里,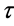 表示样本序列的偏度(skewness)统计量,对于大样本,在零假设为正态分布条件下,均值为0,标准方差为
表示样本序列的偏度(skewness)统计量,对于大样本,在零假设为正态分布条件下,均值为0,标准方差为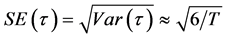 ;
; 表示样本序列的峰度(kurtosis)统计量,对于大样本情况,在零假设为正态分布条件下,均值为3,标准方差为
表示样本序列的峰度(kurtosis)统计量,对于大样本情况,在零假设为正态分布条件下,均值为3,标准方差为 ;
; 是样本序列的大小。估计值
是样本序列的大小。估计值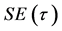 和
和 定义如下:
定义如下:
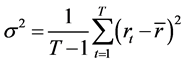 (3)
(3)
 (4)
(4)
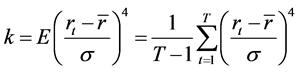 (5)
(5)
3.2. Ljung-Box自相关性检验
假设样本序列 是一个独立同分布(iid)时间序列,Box & Pierce (1970) [12] 提出了一个统计量
是一个独立同分布(iid)时间序列,Box & Pierce (1970) [12] 提出了一个统计量 来检验时间序列
来检验时间序列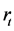 是否为自相关序列,零假设为
是否为自相关序列,零假设为 ;备择假设为
;备择假设为 ,
, 。统计量
。统计量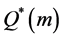 渐近地趋向于自由度为
渐近地趋向于自由度为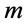 的卡方分布。
的卡方分布。
 ,
,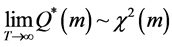 (6)
(6)
Ljung & Box (1978) [13] 对统计量 进行了修改,而创造出了一个新的统计量
进行了修改,而创造出了一个新的统计量 ,以增加对于有限样本检验的力度。检验时间序列
,以增加对于有限样本检验的力度。检验时间序列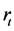 是否为自相关序列,拒绝零假设
是否为自相关序列,拒绝零假设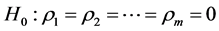 的条件是
的条件是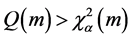 ,当
,当
 ,
,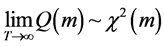 (7)
(7)
这里, 是自由度为
是自由度为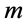 的卡方分布,置信度水平为
的卡方分布,置信度水平为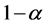 ;
; 是
是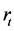 与滞后
与滞后 阶变量
阶变量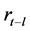 之间的自相关系数(autocorrelation coefficient, AC)。
之间的自相关系数(autocorrelation coefficient, AC)。
当 被定义为一个平稳序列时,一般会有
被定义为一个平稳序列时,一般会有 ,
, ,
,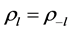 ,
, 。如果对于
。如果对于 ,
,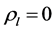 ,那么,平稳序列
,那么,平稳序列 就不是序列自相关的(Tsay, 2005) [14] 。假如滞后阶数
就不是序列自相关的(Tsay, 2005) [14] 。假如滞后阶数 ,则自相关系数由下式得到:
,则自相关系数由下式得到:
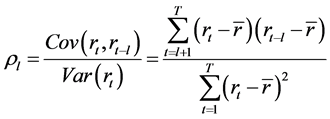 ,
, (8)
(8)
如果变量 是序列自相关的,则具有
是序列自相关的,则具有 阶滞后项的
阶滞后项的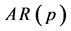 自相关模型为(Tsay, 2005) [14] :
自相关模型为(Tsay, 2005) [14] :
 (9)
(9)
变量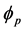 是序列
是序列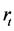 与滞后
与滞后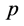 阶的序列
阶的序列 之间的偏相关系数(partial autocorrelation, PAC)。
之间的偏相关系数(partial autocorrelation, PAC)。
3.3. ADF单位根检验
单位根检验就是测试一个时间序列 是否为平稳序列。一个时间序列
是否为平稳序列。一个时间序列 是平稳的,当且仅当其
是平稳的,当且仅当其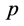 阶自相关模型
阶自相关模型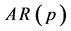 具有性质:如果
具有性质:如果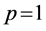 ,那么
,那么 ,且
,且 ,
, ,
, ,对于任何的
,对于任何的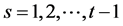 ,都有
,都有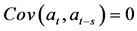 ;相反地,如果
;相反地,如果 ,那么序列
,那么序列 就是非平稳序列或者是一个随机游走过程。为了检验单位根,假设零假设为
就是非平稳序列或者是一个随机游走过程。为了检验单位根,假设零假设为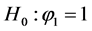 ,备择假设为
,备择假设为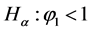 。Dickey-Fuller检验方法 (Dickey &Fuller,1979) [15] 通常被用来作为单位根检验的工具,也称为DF检验,DF统计量定义如下:
。Dickey-Fuller检验方法 (Dickey &Fuller,1979) [15] 通常被用来作为单位根检验的工具,也称为DF检验,DF统计量定义如下:
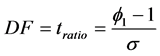 ,
,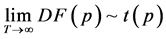 (10)
(10)
 ,
, (11)
(11)
增强ADF检验(Dickey&Fuller, 1981) [16] ,也称为ADF检验(Augmented Dickey Fuller),是单位根检验最常用的形式,其零假设为 ,共有三种ADF检验模式:
,共有三种ADF检验模式:
 (12)
(12)
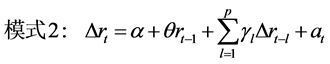 (13)
(13)
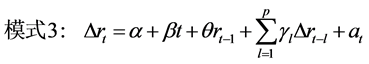 (14)
(14)
当进行ADF检验时,按照模式3、模式2、模式1的顺序进行检验比较好(Jeffrey, 2000) [17] 。如果一个水平变量是平稳的,它就是一个 变量;如果一个变量的
变量;如果一个变量的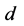 阶差分是平稳的,它将是一个
阶差分是平稳的,它将是一个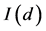 变量。
变量。
3.4. 长期协整关系检验
假设两个时间序列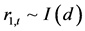 ,
,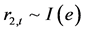 ,那么,如果存在一个线性组合
,那么,如果存在一个线性组合 ,满足
,满足 ,
, ,则
,则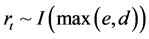 (Li & Ye, 2000) [18] 。当两个序列
(Li & Ye, 2000) [18] 。当两个序列 ,
,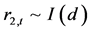 ,
, ,都是非平稳序列,如果存在一个线性组合
,都是非平稳序列,如果存在一个线性组合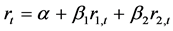 ,
, ,
,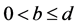 ,那么,它们的线性组合
,那么,它们的线性组合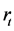 就是一个
就是一个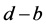 阶协整向量,服从
阶协整向量,服从 ;如果
;如果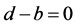 ,那么,线性组合
,那么,线性组合 就是一个平稳序列或者协整序列(cointegration)。协整关系就是多个非平稳序列所组成的一个线性组合的长期平稳均衡关系(Engle & Granger, 1987) [19] 。
就是一个平稳序列或者协整序列(cointegration)。协整关系就是多个非平稳序列所组成的一个线性组合的长期平稳均衡关系(Engle & Granger, 1987) [19] 。
Engle & Granger (1987) [19] 建立了一个两步法协整检验方法,以两个时间序列之间的协整关系为例:第一,建立一个普通最小二乘(OLS)回归模型 ;第二,检验其误差项序列
;第二,检验其误差项序列 是否在
是否在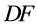 或
或 检验下是平稳序列。由于最小二乘回归运算对于序列的平稳性有影响,所以,Jeffrey (2000) [17] 建议使用一个更高的标准,Davidson & MacKinnon (1993) [20] 门限值标准被推荐用来进行平稳性检验,即在1%、5%、10%概率水平下,
检验下是平稳序列。由于最小二乘回归运算对于序列的平稳性有影响,所以,Jeffrey (2000) [17] 建议使用一个更高的标准,Davidson & MacKinnon (1993) [20] 门限值标准被推荐用来进行平稳性检验,即在1%、5%、10%概率水平下,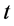 统计量的取值不能小于−4.32、−3.78、−3.50的绝对值。
统计量的取值不能小于−4.32、−3.78、−3.50的绝对值。
Johansen & Juselius协整检验(Johansen, 1988 [21] ; Johansen & Juselius, 1990 [22] )是另外一种协整检验方法,该检验方法的关键是:当 时,通过检验矩阵
时,通过检验矩阵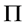 的秩或者阶数,来检验是否存在
的秩或者阶数,来检验是否存在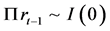 。如果矩阵
。如果矩阵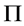 的秩是
的秩是 ,即
,即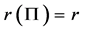 ,那么,就存在
,那么,就存在 个协整关系。特征值(eigen value)检验和迹统计(trace static)检验是Johansen & Juselius协整检验的两种方法。其中:
个协整关系。特征值(eigen value)检验和迹统计(trace static)检验是Johansen & Juselius协整检验的两种方法。其中:
 ,或
,或 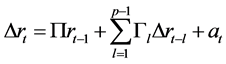 (15)
(15)
这里,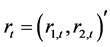 是一个列向量,
是一个列向量,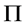 和
和 是两个相关系数矩阵。
是两个相关系数矩阵。
3.5. 短期协整关系检验
如果长期协整关系模型的误差项是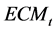 ,并且是一个平稳序列,
,并且是一个平稳序列,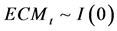 ,那么,协整模型与向量误差修正模型(VECM) 之间具有同构关系(Engle & Granger, 1987) [23] 。VECM向量误差修正模型主要揭示时间序列模型的长期误差是如何通过短期关系来得到修正的。VECM向量误差修正模型一般形式:
,那么,协整模型与向量误差修正模型(VECM) 之间具有同构关系(Engle & Granger, 1987) [23] 。VECM向量误差修正模型主要揭示时间序列模型的长期误差是如何通过短期关系来得到修正的。VECM向量误差修正模型一般形式:
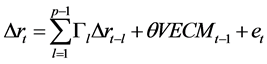 (16)
(16)
VECM向量误差修正模型不仅可以揭示两个时间变量之间是否存在短期协整关系,也可以被用来检验两个时间变量之间是否存在短期Granger因果关系。
3.6. 选择优化滞后阶数
有三种信息准则被用来检验回归模型滞后阶数的长度,分别是:Akaike信息准则 (AIC)、Schwarz信息准则 (SIC)、Hannan-Quinn信息准则(HIC)。与SIC、HIC相比,AIC是一个更好的信息准则,特别是对于滞后阶数长度较小的模型更具优势(Liew, 2004)。滞后阶数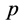 的选择将按照使AIC统计量最小的原则选取(Liew, 2004) [24] :
的选择将按照使AIC统计量最小的原则选取(Liew, 2004) [24] :
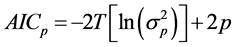 ,其中
,其中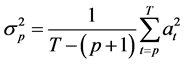 (17)
(17)
3.7. Granger因果检验
Granger因果关系(Granger, 1980) [19] 揭示的是:一个时间序列 在与时间
在与时间 相关的信息集
相关的信息集
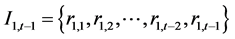 已知的条件下,是否对另外一个时间序列
已知的条件下,是否对另外一个时间序列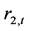 具有影响?根据Jeffrey (2000) [17] 的论述,假设信息集
具有影响?根据Jeffrey (2000) [17] 的论述,假设信息集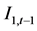 和
和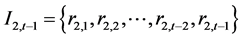 是两个与时间
是两个与时间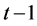 相关的信息集,如果能够显著检验到存在关系
相关的信息集,如果能够显著检验到存在关系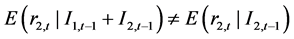 ,或
,或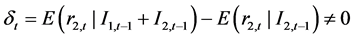 ,那么,
,那么,
就可以说时间序列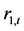 是时间序列
是时间序列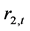 的一个Granger原因。通常,VAR向量自回归模型是检验两个时间序列之间是否存在Granger因果关系的好方法(Jeffrey, 2000) [17] 。
的一个Granger原因。通常,VAR向量自回归模型是检验两个时间序列之间是否存在Granger因果关系的好方法(Jeffrey, 2000) [17] 。
3.8. GARCH(1,1)模型
广义自回归条件异方差GARCH模型是处理单变量时间序列异方差问题的通用工具。假如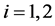 ,时间序列变量
,时间序列变量 代表第
代表第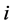 个资产的收益指数,
个资产的收益指数,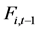 代表第
代表第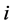 个资产与时间
个资产与时间 相关的信息集,那么,条件自回归模型AR(1)就可以定义为:
相关的信息集,那么,条件自回归模型AR(1)就可以定义为:
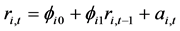 ,或
,或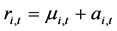 ,
,  ,
,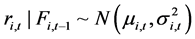 (18)
(18)
当 ,
, 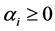 ,
,  ,
,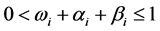 时,GARCH(1,1)模型就可以定义为
时,GARCH(1,1)模型就可以定义为
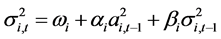 ,
,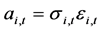 ,
,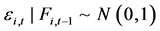 ,
, (19)
(19)
这里,长期静态方差是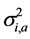 ,系数
,系数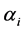 与
与 满足如下关系式:
满足如下关系式:
 ,
,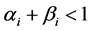 (20)
(20)
3.9. DCC-GARCH(1,1)模型
当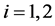 时,对于两个误差变量
时,对于两个误差变量 ,假设
,假设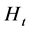 为协方差矩阵,
为协方差矩阵,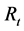 为相关系数矩阵,
为相关系数矩阵, 为协方差对角矩阵,
为协方差对角矩阵,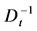 是协方差对角矩阵的逆矩阵,那么,矩阵
是协方差对角矩阵的逆矩阵,那么,矩阵 、
、 、
、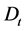 之间具有如下关系:
之间具有如下关系:
 ,
, 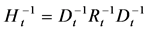 ,
,  ,
, (21)
(21)
类似地,当 时,对于两个标准误差变量
时,对于两个标准误差变量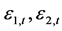 ,假设
,假设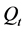 为协方差矩阵,
为协方差矩阵, 为相关系数矩阵,
为相关系数矩阵, 为协方差对角矩阵,
为协方差对角矩阵, 为协方差对角矩阵的逆矩阵,那么,矩阵
为协方差对角矩阵的逆矩阵,那么,矩阵 、
、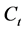 、
、 之间具有如下关系:
之间具有如下关系:
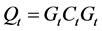 ,
, 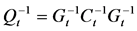 ,
,  ,
,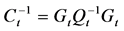 (22)
(22)
因为条件相关系数 ,
,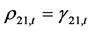 ,所以,条件相关系数矩阵
,所以,条件相关系数矩阵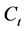 与
与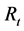 等价,具有关系
等价,具有关系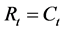 ,正因如此,协方差矩阵
,正因如此,协方差矩阵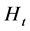 可以表示为:
可以表示为:
 (23)
(23)
以上关系式表示,可以把对于AR自回归模型误差项 、
、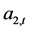 的条件异方差的讨论,转化为对于GARCH模型下标准误差变量
的条件异方差的讨论,转化为对于GARCH模型下标准误差变量 、
、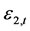 的条件异方差的讨论。根据Engle (2002) [25] 的定义,当考虑条件信息集合时,DCC-GARCH(1,1)模型可以定义为:
的条件异方差的讨论。根据Engle (2002) [25] 的定义,当考虑条件信息集合时,DCC-GARCH(1,1)模型可以定义为:
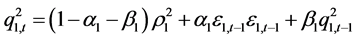 (24)
(24)
 (25)
(25)
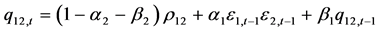 (26)
(26)
 (27)
(27)
得到了方差 和协方差
和协方差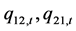 ,动态条件相关系数(DCC)可以通过如下公式计算:
,动态条件相关系数(DCC)可以通过如下公式计算:
 ,
, ,且
,且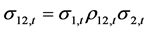 ,
, (28)
(28)
在对参数 进行最大似然估计(MLE)时,必须满足如下条件:
进行最大似然估计(MLE)时,必须满足如下条件:
 ,
, (29)
(29)
3.10. Copula联合分布与尾部依赖关系
Copula函数是用来测定多个变量之间相互依赖关系的一类联合分布函数,由Sklar (1959) [26] 首次提出。假设变量 和
和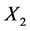 是两个随机变量,它们的边际分布函数由如下概率函数来决定:
是两个随机变量,它们的边际分布函数由如下概率函数来决定:
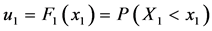 ,
, (30)
(30)
显然, ,
,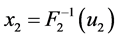 。对于任何联合概率函数
。对于任何联合概率函数 ,二元Copula函数
,二元Copula函数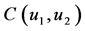 被定义为:
被定义为:
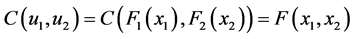 (31)
(31)
假设随机变量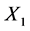 和
和 的边际密度函数是
的边际密度函数是 和
和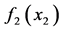 ,联合密度分布函数是
,联合密度分布函数是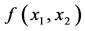 ,它们的Copula密度函数是
,它们的Copula密度函数是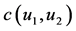 ,那么:
,那么:
 (32)
(32)
Copula密度函数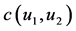 与普通概率密度函数
与普通概率密度函数 不同,因为Copula密度函数
不同,因为Copula密度函数 的值总为正,这就说明Copula密度函数在尾部具有较高的取值,有利于表示尾部依赖关系。对于任何随机变量
的值总为正,这就说明Copula密度函数在尾部具有较高的取值,有利于表示尾部依赖关系。对于任何随机变量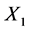 和
和 ,下尾(lower tail)和上尾(upper tail)依赖系数被定义为:
,下尾(lower tail)和上尾(upper tail)依赖系数被定义为:
 ,
, ,
, ,
, (33)
(33)
 ,
,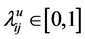 ,
,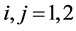 ,
,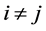 (34)
(34)
第一,Clayton Copula分布函数。Clayton Copula分布函数(Clayton, 1978) [27] 关注的重点是下尾依赖关系。当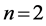 时,基于Clayton Copula累积分布函数,Clayton Copula密度函数被定义为(Alexander, 2008) [11] :
时,基于Clayton Copula累积分布函数,Clayton Copula密度函数被定义为(Alexander, 2008) [11] :
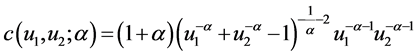 (35)
(35)
Clayton Copula的下尾和上尾依赖系数被定义为:
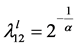 ,
, 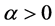 ,
, ;
; (36)
(36)
第二,GumbelCopula分布函数。GumbelCopula分布函数(Gumbel,1960) [28] 关注的重点是上尾依赖关系。当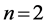 时,基于Gumbel Copula累积概率分布函数,Gumbel Copula密度函数可以表示为(Alexander, 2008) [11] :
时,基于Gumbel Copula累积概率分布函数,Gumbel Copula密度函数可以表示为(Alexander, 2008) [11] :
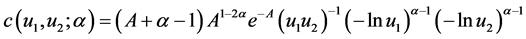 (37)
(37)
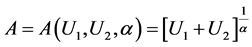 ,
,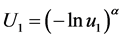 ,
, (38)
(38)
Gumbel Copula的下尾和上尾依赖系数被定义为:
 ;
;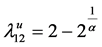 ,
,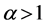 (39)
(39)
3.11. 参数的最大似然估计
最大似然估计(MLE)通常被用来估计建立数学模型所必要的参数值。
第一,DCC-GARCH模型参数估计。Engle (2002) [25] 提出,当使用最大似然估计来获取DCC-GARCH模型参数时,应该从初始误差向量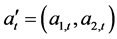 的联合密度函数出发。其对数MLE方程可以被分解为方差方程和相关系数方程两个部分,例如:
的联合密度函数出发。其对数MLE方程可以被分解为方差方程和相关系数方程两个部分,例如: 。其中:方差估计方程
。其中:方差估计方程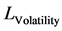 可以表示为:
可以表示为:
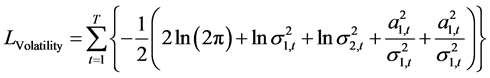 (40)
(40)
基于标准误差向量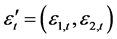 ,相关系数估计方程
,相关系数估计方程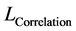 可以表示为:
可以表示为:
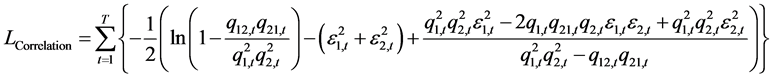 (41)
(41)
第二,学生t分布函数自由度的估计,按照对数MLE方程:
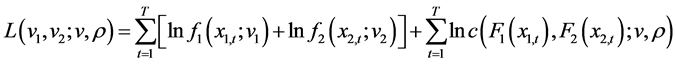 (42)
(42)
学生t分布的对数MLE方程也可以通过两个步骤来实现,所有参数估计参照:
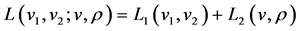 (43)
(43)
第三,其它参数估计。对于其它参数,例如:Gaussian Copula分布函数、Clayton Copula分布函数、Gumbel Copula分布函数,它们都与学生t分布参数估计类似,通过对其密度函数的对数MLE方程进行估计,容易得到它们的参数。
4. 协整和因果关系检验结果
4.1. 描述性统计值
表2列出了以上证综指和深证成指日收盘价指数为基础计算的收益指数的描述性统计值。很明显,上证收益指数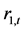 的均值为1.000328,深证收益指数
的均值为1.000328,深证收益指数 的均值为1.00049,尽管两市收益率指数非常接近,但上证收益指数均值稍高。
的均值为1.00049,尽管两市收益率指数非常接近,但上证收益指数均值稍高。
偏度 (skewness)分析发现,上证收益指数和深证收益指数的偏度都小于0,表示都具有左偏性。峰度(kurtosis)分析发现,上证收益指数和深证收益指数的峰度都大于3,表示都具有尖峰性。正态分布Jarque-Bera检验发现,JB统计值拒绝零假设,即拒绝正态分布假设,表示上证收益指数和深证收益指数都不是严格服从正态分布。偏度、峰度、非正态性分布特征,都表示上证收益指数和深证收益指数具有厚尾或长尾分布现象。
4.2. 序列自相关性检验
表3列出了上证收益指数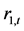 的Ljung-Box统计量(Ljung & Box,1978) [13] 自相关性检验结果:在1%水平下,自相关系数
的Ljung-Box统计量(Ljung & Box,1978) [13] 自相关性检验结果:在1%水平下,自相关系数 ,
,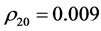 ,
, ,都不为零,显然,上证收益指数
,都不为零,显然,上证收益指数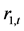 是一个具有自相关性的时间序列,适合建立AR自相关模型。
是一个具有自相关性的时间序列,适合建立AR自相关模型。
表3列出了深证收益指数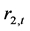 的Ljung-Box统计量(Ljung & Box, 1978) [13] 自相关性检验结果:在1%水平下,自相关系数
的Ljung-Box统计量(Ljung & Box, 1978) [13] 自相关性检验结果:在1%水平下,自相关系数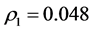 ,
,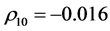 ,
,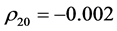 ,
, ,表明深证收益指数
,表明深证收益指数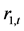 是一个具有自相关性的时间序列,适合建立AR自相关模型。
是一个具有自相关性的时间序列,适合建立AR自相关模型。
Table 2. Descriptive statistics of the both return indices from Shanghai Composite Index and Shenzhen Component Index
表2. 沪深两市股票价格指数上证综指和深证成指收益指数基本描述性统计
Table 3. Autocorrelation test for Shanghai and Shenzhen stock return indices
表3. 上证收益指数和深证股票收益指数自相关性检验
备注:1) AC表示自相关系数;2) Q表示Ljung-Box统计量;3) P表示 检验概率;4) 括号中的数字为滞后阶数。
检验概率;4) 括号中的数字为滞后阶数。
4.3. 序列平稳性检验
假设 表示上证综指价格指数,
表示上证综指价格指数,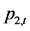 表示深证成指价格指数,
表示深证成指价格指数, 表示上证综指价格指数的收益指数,
表示上证综指价格指数的收益指数, 表示深证成指价格指数的收益指数。表4为四个变量在AIC信息准则下的ADF单位根检验结果。容易发现,在1%、5%、10%等三种概率水平下,三种模型都表明上证综指价格指数变量
表示深证成指价格指数的收益指数。表4为四个变量在AIC信息准则下的ADF单位根检验结果。容易发现,在1%、5%、10%等三种概率水平下,三种模型都表明上证综指价格指数变量 和深证成指价格指数变量
和深证成指价格指数变量 的单位根检验都未通过,它们的水平变量
的单位根检验都未通过,它们的水平变量 、
、 为非平稳变量。相反地,在1%概率水平下,上证收益指数
为非平稳变量。相反地,在1%概率水平下,上证收益指数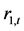 和深证收益指数
和深证收益指数 的单位根检验在模型3和模型2下都获得通过,即它们为平稳变量。鉴于此,本文中的分析数据将以上证收益指数
的单位根检验在模型3和模型2下都获得通过,即它们为平稳变量。鉴于此,本文中的分析数据将以上证收益指数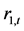 和深证收益指数
和深证收益指数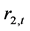 为基础进行分析。
为基础进行分析。
4.4. Johansen-Juselius协整检验
Johansen-Juselius协整关系检验是考察两个以上非平稳时间序列之间是否可以构成一个平稳线性组合方程的有效工具。两个或者多个非平稳时间序列之间具有Johansen-Juselius协整关系,如果它们之间的线性组合是平稳序列。
表5列出了上证收益指数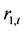 和深证收益指数
和深证收益指数 之间的Johansen-Juselius协整检验结果。由于时间序列
之间的Johansen-Juselius协整检验结果。由于时间序列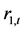 和
和 都是平稳时间序列,所以,它们之间的协整关系很容易得到验证,Johansen-Juselius协整检验结果表明,它们之间具有长期协整关系。
都是平稳时间序列,所以,它们之间的协整关系很容易得到验证,Johansen-Juselius协整检验结果表明,它们之间具有长期协整关系。
表6列示出了上证收益指数与深证收益指数之间的长期协整线性方程。两个方程表明变量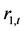 和
和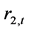 之间的长期协整关系在1%概率水平下t检验显著有效。
之间的长期协整关系在1%概率水平下t检验显著有效。
协整关系表现了两个变量之间长期的线性关系,反映了两个变量之间比较平稳的长期均衡关系。协整关系的误差项反映了长期线性关系误差,表现了长期关系中不协调的因素,该误差项将被用于VECM
Table 4. ADF unit root test under AIC criterion for Shanghai composite index and Shenzhen component index and their return indices
表4. 沪深两市股票价格指数上证综指和深证成指及其收益指数在AIC准则下的ADF单位根检验
备注:1) 以上检验最大滞后阶数为29,由EVIEWS软件自动选择;2) ADF检验模型3既包含趋势项又包含截距项,模型2仅包含截距项,模型1既不包含趋势项又不包含截距项;3) SIC、HIC信息准则结果与AIC一致。
Table 5. Johansen-Juselius cointegration test for the both return indices of Shanghai composite index and Shenzhen component index
表5. 上证收益指数与深证收益指数之间的Johansen-Juselius协整关系检验
备注: 1) 一阶差分滞后区间为1到4;2) 迹检验和最大特征值检验表明在三种趋势假设和五种检验类型情况下至少有1个或者2个协整方程,在5%概率水平下拒绝没有协整方程的假设。
短期协整关系的讨论。
4.5. 长期Granger因果关系
表7列出了变量 和
和 之间两个向量自回归(VAR)模型回归结果。VAR向量自回归模型适合用于进行Granger因果关系检验。结果表明:在1%概率水平下,滞后一阶变量
之间两个向量自回归(VAR)模型回归结果。VAR向量自回归模型适合用于进行Granger因果关系检验。结果表明:在1%概率水平下,滞后一阶变量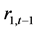 对变量
对变量 的t检验显著有效,说明变量
的t检验显著有效,说明变量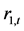 是变量
是变量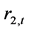 的一个Granger原因;相应地,在10%概率水平下,滞后一阶变量
的一个Granger原因;相应地,在10%概率水平下,滞后一阶变量 对变量
对变量 的t检验显著有效,说明变量
的t检验显著有效,说明变量 是变量
是变量 的一个Granger原因。这说明,上证收益指数
的一个Granger原因。这说明,上证收益指数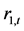 与深证收益指数
与深证收益指数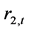 之间具有双向Granger因果关系。尽管如此,上证收益指数
之间具有双向Granger因果关系。尽管如此,上证收益指数 对深证收益指数
对深证收益指数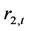 的Granger因果关系影响力更强,影响效果更明显。
的Granger因果关系影响力更强,影响效果更明显。
4.6. 短期Granger因果关系
表8列出了上证收益指数与深证收益指数之间的VECM向量误差修正模型。VECM模型显示:差分滞后项 、
、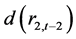 、
、 等,在1%概率水平下,都对
等,在1%概率水平下,都对 项t检验显著有效;相应地,差分滞后项
项t检验显著有效;相应地,差分滞后项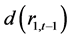 、
、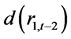 、
、 等,在1%概率水平下,都对
等,在1%概率水平下,都对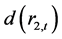 项t检验显著有效。这表明,上证收益指数
项t检验显著有效。这表明,上证收益指数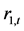 与深证收益指数
与深证收益指数 之间具有显著的短期双向Granger因果关系。
之间具有显著的短期双向Granger因果关系。
因为在1% 概率水平下,误差滞后一阶项 都是t检验显著有效,这表明长期协整关系下的误差项在短期内会得到快速地调整和修正,即长期关系中的不协调部分,在短期内会得到及时调整和修正。
都是t检验显著有效,这表明长期协整关系下的误差项在短期内会得到快速地调整和修正,即长期关系中的不协调部分,在短期内会得到及时调整和修正。
Table 6. Long-run linear cointegration models for the both return indices of Shanghai composite index and Shenzhen component index
表6. 上证收益指数与深证收益指数之间的长期协整关系线性模型
备注: 1) 符号 *、**、***表示在概率水平分别为1%、5%、10%时,t检验显著有效,零假设被拒绝,模型系数不为零。
Table 7. VAR models for the both return indices of Shanghai composite index and Shenzhen component index
表7. 上证收益指数与深证收益指数之间的VAR向量自回归模型
备注: 1) 符号 *、**、***表示在概率水平分别为1%、5%、10%时,t检验显著有效,零假设被拒绝,模型系数不为零。2) c是模型截距项。
Table 8. VECM models for the both return indices of Shanghai composite index and Shenzhen component index
表8. 上证收益指数与深证收益指数之间的VECM 向量误差修正模型
备注: 1) 符号 *、**、***表示在概率水平分别为1%、5%、10%时,t检验显著有效,零假设被拒绝,模型系数不为零;2)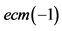 是长期协整关系线性回归方程误差项的滞后一阶项目,因为有两个方程,所以有两个误差项
是长期协整关系线性回归方程误差项的滞后一阶项目,因为有两个方程,所以有两个误差项 。
。
5. DCC动态相关性和Copula函数尾依赖检验结果
5.1. GARCH(1,1) 模型
表9列出了上证收益指数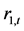 和深证收益指数
和深证收益指数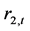 的滞后一阶自回归模型
的滞后一阶自回归模型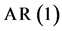 和一般自回归条件异方差模型
和一般自回归条件异方差模型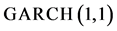 。所有参数的对数最大似然估计均依据单变量正态分布来估计。很显然,两个收益指数
。所有参数的对数最大似然估计均依据单变量正态分布来估计。很显然,两个收益指数 和
和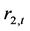 的一般自回归条件异方差模型
的一般自回归条件异方差模型 的参数在1%概率值下都是显著有效的。
的参数在1%概率值下都是显著有效的。
两个 模型中,由于GARCH项变量
模型中,由于GARCH项变量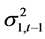 和
和 的系数
的系数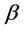 值都很大,对动态方差
值都很大,对动态方差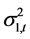 和
和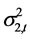 影响很大,这说明上证收益指数和深证收益指数的动态方差都具有很强的聚集效应,并且从时间变量
影响很大,这说明上证收益指数和深证收益指数的动态方差都具有很强的聚集效应,并且从时间变量 到
到 ,两个收益指数的波动性都具有扩散和溢出效应。
,两个收益指数的波动性都具有扩散和溢出效应。
两个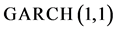 模型中,由于ARCH项变量
模型中,由于ARCH项变量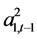 和
和 的系数
的系数 值都不为零,这说明上证收益指数和深证收益指数的自回归模型误差项的滞后项对于动态方差
值都不为零,这说明上证收益指数和深证收益指数的自回归模型误差项的滞后项对于动态方差 和
和 也有一定影响。
也有一定影响。
截距项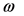 的值很小,表明长期平均波动性影响较小。
的值很小,表明长期平均波动性影响较小。
图1是上证收益指数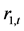 的
的 模型下的动态条件方差
模型下的动态条件方差 曲线图示。图2是深证收益指数
曲线图示。图2是深证收益指数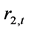 的
的 模型下的动态条件方差
模型下的动态条件方差 曲线图示。
曲线图示。
统计分析显示,上证收益指数的动态方差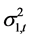 和深证收益指数的动态方差
和深证收益指数的动态方差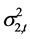 的均值分别为0.0155、0.0175;标准误差分别为0.0064、0.0062;偏度分别为1.2269、1.2366;峰度分别为4.0321、3.9471;二者之间的相关系数为0.9681。显然,二者的各项参数之间具有一定的相似性,并且相关性很高。
的均值分别为0.0155、0.0175;标准误差分别为0.0064、0.0062;偏度分别为1.2269、1.2366;峰度分别为4.0321、3.9471;二者之间的相关系数为0.9681。显然,二者的各项参数之间具有一定的相似性,并且相关性很高。
5.2. DCC模型
通常,GARCH模型主要用于观察单变量序列的动态条件方差;而DCC模型主要用于观察多变量序列之间的动态条件相关系数。为了估计DCC模型的动态条件相关系数,第一步就是估计GARCH(1, 1)模型下的动态条件方差、以及标准误差,然后根据标准误差估计DCC模型的参数。
为了估计DCC模型的参数,需要先得到标准误差项 之间的静态相关系数
之间的静态相关系数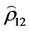 作为初值。实际验证发现收益指数变量
作为初值。实际验证发现收益指数变量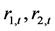 之间的静态相关系数值为0.9330;自回归AR(1)模型误差变量
之间的静态相关系数值为0.9330;自回归AR(1)模型误差变量 之间的静态相关系数值为0.9332;GARCH(1,1)模型标准误差变量
之间的静态相关系数值为0.9332;GARCH(1,1)模型标准误差变量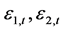 之间的静态相关系数值为0.9333。由于DCC模型参数的对数最大似然估计需要,静态相关系数初值就定义为
之间的静态相关系数值为0.9333。由于DCC模型参数的对数最大似然估计需要,静态相关系数初值就定义为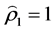 ,
,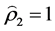 ,
,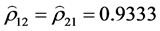 。
。
表10列出了DCC的模型估计结果。在1%概率水平下,参数的t检验结果都显著有效。模型中,变量 是标准误差
是标准误差 的动态条件方差;变量
的动态条件方差;变量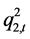 表现了标准误差
表现了标准误差 的动态条件方差;变量
的动态条件方差;变量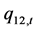 和
和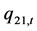 表现了两个标准误差
表现了两个标准误差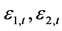 之间的动态条件协方差。在得到动态DCC模型参数之后,动态条件相关系数(dynamic conditional correlations)的计算就参照公式
之间的动态条件协方差。在得到动态DCC模型参数之后,动态条件相关系数(dynamic conditional correlations)的计算就参照公式 和
和 进行。
进行。
Table 9. AR(1) and GARCH(1,1) regressive models for the both return indices of Shanghai composite index and Shenzhen component index
表9. 上证收益指数与深证收益指数的AR(1)和GARCH(1,1) 回归模型
备注: 1)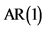 和
和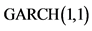 模型参数的对数最大似然估计以正态分布密度函数为基础; 2) 参考自相关性检验结果,自回归模型均使用滞后一阶
模型参数的对数最大似然估计以正态分布密度函数为基础; 2) 参考自相关性检验结果,自回归模型均使用滞后一阶 模型;3)
模型;3)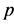 是z-statistic的概率值;4) 初始GARCH值满足条件
是z-statistic的概率值;4) 初始GARCH值满足条件 , 最大似然估计参数满足
, 最大似然估计参数满足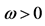 ,
,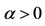 ,
,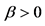 ,
,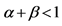 ,对数最大似然估计参数计算依据单变量正态分布;5) 标准误差计算来自公式
,对数最大似然估计参数计算依据单变量正态分布;5) 标准误差计算来自公式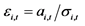 ,其中
,其中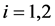 。
。
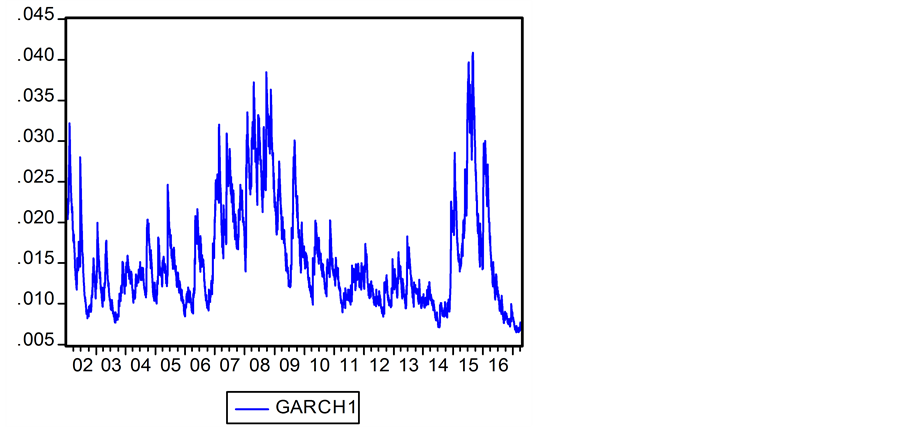
Figure 1. GARCH(1,1) curve of return index from Shanghai Composite Index
图1. 上证收益指数GARCH(1,1)模型曲线图示

Figure 2. GARCH(1,1) curve of return index from Shenzhen Component Index
图2. 深证收益指数GARCH(1,1)模型曲线图示
Table 10. DCC-GARCH(1,1) models from the standard residuals
表10. 由标准误差项所得到的DCC-GARCH(1,1) 模型
备注: 1) MLL是对数最大似然估计(maximum log likelihood)值;AIC是Akaike信息准则值;SIC是Schwarz信息准则值;HIC 是Hannan-Quinn信息准则值。
显然,与GARCH(1,1)模型类似,在滞后时间变量为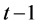 时的动态条件方差和协方差变量
时的动态条件方差和协方差变量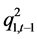 、
、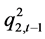 、
、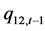 、
、 对于今后在时间变量为
对于今后在时间变量为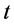 时的动态条件方差和协方差
时的动态条件方差和协方差 、
、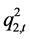 、
、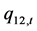 、
、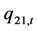 都有显著、且较大的影响,说明聚集效应、扩散效应、或溢出效应是收益指数波动性的主要特征。
都有显著、且较大的影响,说明聚集效应、扩散效应、或溢出效应是收益指数波动性的主要特征。
描述性统计分析发现,动态条件相关系数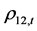 ,
,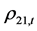 的均值,也即DCC均值分别为0.935334,它们与
的均值,也即DCC均值分别为0.935334,它们与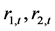 之间的静态相关系数值0.9330,
之间的静态相关系数值0.9330,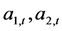 之间的静态相关系数值0.9332,
之间的静态相关系数值0.9332, 之间的静态相关系数值0.9333,都非常接近,误差小于0.005。
之间的静态相关系数值0.9333,都非常接近,误差小于0.005。
动态条件相关系数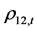 ,
,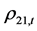 的值表现了三组变量
的值表现了三组变量 、
、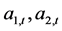 、
、 中每组变量内部两个变量之间相关系数的变化过程。统计显示,DCC最小值为0.8345,最大值为1,说明上证收益指数与深证收益指数之间具有很高的相关性。但是,静态相关系数无法像动态相关系数一样反映两个收益指数之间相关性随时间动态变化的情况。
中每组变量内部两个变量之间相关系数的变化过程。统计显示,DCC最小值为0.8345,最大值为1,说明上证收益指数与深证收益指数之间具有很高的相关性。但是,静态相关系数无法像动态相关系数一样反映两个收益指数之间相关性随时间动态变化的情况。
图3表现了两个标准误差项在DCC模型下的动态条件协方差 和
和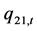 曲线图示。图4表现了两个标准误差项在DCC模型下的动态条件相关系数
曲线图示。图4表现了两个标准误差项在DCC模型下的动态条件相关系数 和
和 曲线图示。条件相关系数
曲线图示。条件相关系数 和
和 曲线反映了上证收益指数
曲线反映了上证收益指数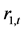 与深证收益指数
与深证收益指数 之间的动态相关关系。
之间的动态相关关系。
条件相关系数 (与
(与 一致重合)与异方差
一致重合)与异方差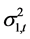 和
和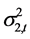 之间具有负相关性,相关系数值分别为−0.2124、−0.2308,这表明,当股票市场波动性较小时,两市之间相关性较强;反之,当股票市场波动性较强时,两市之间相关性较弱。
之间具有负相关性,相关系数值分别为−0.2124、−0.2308,这表明,当股票市场波动性较小时,两市之间相关性较强;反之,当股票市场波动性较强时,两市之间相关性较弱。
5.3. Copula尾部依赖关系
首先,考虑标准误差项满足Gaussian正态分布的情况。理论上来说,标准误差项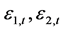 服从
服从 正态分布。但是,在实证分析中,由于理论值与实际值之间存在差异,所以,为了提高计算的精度,需要对实际值重新计算正态分布的均值
正态分布。但是,在实证分析中,由于理论值与实际值之间存在差异,所以,为了提高计算的精度,需要对实际值重新计算正态分布的均值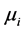 、方差
、方差 ,以及联合分布相关系数
,以及联合分布相关系数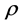 。
。
其次,考虑标准误差项满足学生t分布的情况。从之前的分析已经知道,两个收益指数并不完全符合正态分布,而具有厚尾分布特点,所以,我们也要在学生t分布环境下进行分析。
表11列出了标准误差项在Gaussian正态分布和学生t分布下的参数估计值。在Gaussian正态分布情
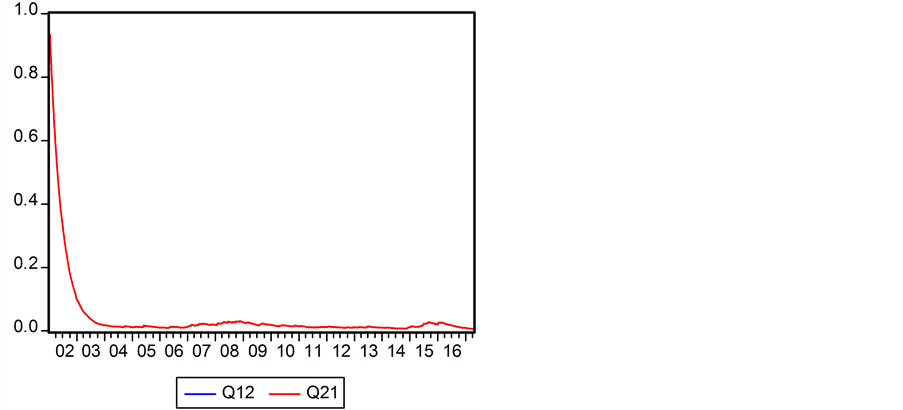
Figure 3. Dynamic conditional covariance curve of the standard residuals based on DCC models
图3. DCC模型下标准误差项的动态条件协方差曲线图示
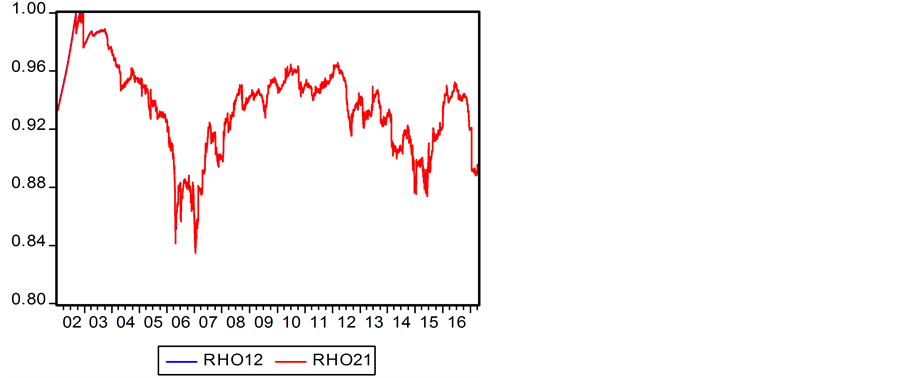
Figure 4. Dynamic conditional correlation curve of the standard residuals based on DCC models
图4. DCC模型下标准误差项的动态条件相关系数曲线图示
Table 11. Parameter estimated values of Gaussian normal distribution and Student-t distribution from the standard residuals
表11. 标准误差项在Gaussian正态分布和学生t分布下的参数估计值
况下,标准误差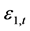 的均值和方差分别为
的均值和方差分别为 、
、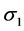 ;标准误差
;标准误差 的均值和方差分别为
的均值和方差分别为 、
、 ;
; 为联合分布相关系数。在学生t分布下,标准误差
为联合分布相关系数。在学生t分布下,标准误差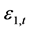 和
和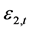 的学生t分布自由度分别为
的学生t分布自由度分别为 ,联合分布的自由度为
,联合分布的自由度为 、相关系数为
、相关系数为 。这些参数将被用来为标准误差
。这些参数将被用来为标准误差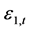 和
和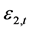 定义Gaussian边际分布和学生t边际分布。
定义Gaussian边际分布和学生t边际分布。
根据已经估计出的参数,就可以很容易地计算出标准误差变量 和
和 在Gaussian正态分布和学生t分布下的单变量概率密度函数值,以及单变量概率分布函数值。据此,就可以估计出Clayton Copula和Gumbel Copula的参数值。对于Clayton Copula,必须满足参数
在Gaussian正态分布和学生t分布下的单变量概率密度函数值,以及单变量概率分布函数值。据此,就可以估计出Clayton Copula和Gumbel Copula的参数值。对于Clayton Copula,必须满足参数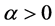 ;而对于Gumbel Copula,必须满足参数
;而对于Gumbel Copula,必须满足参数 。
。
表12列出了在标准误差变量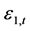 和
和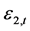 在满足Gaussian正态分布和学生t分布两种情况下,所计算出的Clayton Copula和Gumbel Copula的参数估计值,以及Clayton Copula的下尾分布和Gumbel Copula的上尾分布概率值。
在满足Gaussian正态分布和学生t分布两种情况下,所计算出的Clayton Copula和Gumbel Copula的参数估计值,以及Clayton Copula的下尾分布和Gumbel Copula的上尾分布概率值。
第一,在学生t分布情况下,标准误差变量 和
和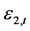 之间的相关系数为0.952569,明显高于在Gaussian正态分布情况下的相关系数0.933391。不仅如此,在学生t分布情况下,Clayton Copula的下尾概率值0.986292和Gumbel Copula的上尾概率值0.980082都高于在Gaussian正态分布情况下Clayton Copula的下尾概率值0.847796和Gumbel Copula的上尾概率值0.815683。这说明,对于两种收益指数来说,学生t分布比Gaussian正态分布具有更好的性质来表现上证收益指数和深证收益指数之间的普通相关性、以及尾部相关性之间的关系。
之间的相关系数为0.952569,明显高于在Gaussian正态分布情况下的相关系数0.933391。不仅如此,在学生t分布情况下,Clayton Copula的下尾概率值0.986292和Gumbel Copula的上尾概率值0.980082都高于在Gaussian正态分布情况下Clayton Copula的下尾概率值0.847796和Gumbel Copula的上尾概率值0.815683。这说明,对于两种收益指数来说,学生t分布比Gaussian正态分布具有更好的性质来表现上证收益指数和深证收益指数之间的普通相关性、以及尾部相关性之间的关系。
第二,在Gaussian正态分布情况下,Clayton Copula下尾分布概率为0.847796,Gumbel Copula上尾分布概率为0.815683;在学生t分布情况下,Clayton Copula下尾分布概率为0.986292,Gumbel Copula
Table 12. Parameter and tail distribution values of Clayton Copula and Gumbel Copula based on Gaussian and Student-t distributions
表12. 基于Gaussian正态分布和学生t分布的Clayton Copula和Gumbel Copula参数和尾分布估计值
上尾分布概率为0.980082。由于不论哪种情况,它们的上尾、下尾分布条件概率值都很高,这说明:在一个指数提高的情况下另外一个指数提高的概率值也很高;反之,在一个指数降低的情况下另外一个指数降低的概率值也很高。这个结果表明,上证收益指数与深证收益指数之间,既存在显著的上尾依赖关系,也存在显著的下尾依赖关系。这一点,与之前得出的上证收益指数与深证收益指数之间的双向格兰杰因果关系完全一致。
6. 小结与今后研究
长期以来,沪深两市股票价格收益指数之间的相关性问题,一直受到研究人员的关注,许多研究者认为沪深两市股票收益指数之间存在很强的相关性,但是,由于很少有人从长期和短期因果关系、长期和短期协整关系、动态相关关系、尾部依赖关系等方面,给出较为全面的分析,所以无法对于沪深两市股票收益指数之间的相关性有一个综合性的理解。本文试图通过对沪深两市股票收益指数之间的相关性进行综合分析,以便对此问题有一个比较全面的认识。
本文从总共3699个上证综指和深证成指日收盘价格指数出发,通过计算,定义了上证收益指数和深证收益指数两个时间序列变量,并以此为基础,研究了沪深两市股票价格收益指数之间的综合相关性问题。
在研究方法上,本文采用Jarque-Bera方法来检验两个时间序列各自是否存在正态分布,采用Ljung-Box方法来检验两个时间序列各自是否存在自相关性,采用ADF方法来检验两个时间序列各自是否为平稳序列;采用Johansen-Juselius方法来检验两个时间序列之间是否存在长期协整关系,采用VAR向量自回归模型来检验两个时间序列之间是否存在长期Granger因果关系,采用VECM向量误差修正模型来检验两个时间变量之间是否存在短期Granger因果关系;采用GARCH(1,1) 模型来计算两个时间序列变量各自的动态条件异方差;采用DCC模型来计算两个时间序列之间的动态条件相关系数;采用Copula联合分布函数来研究两个时间变量彼此之间的尾相关性,其中,Clayton Copula分布函数被用来计算二者之间的下尾依赖关系概率值,Gumbel Copula分布函数被用来计算上尾依赖关系概率值;MLE最大似然估计方法被用来计算各个模型的参数值,其中,在估计Copula函数参数时,Gussian正态分布和学生t分布下两个时间变量的CDF累计概率函数值被作为Copula边际分布函数值加以使用。
对上证收益指数和深证收益指数各自时间序列特征,统计分析发现,上证收益指数与深证收益指数的统计均值非常接近,它们的偏度、峰度、以及非正态性分布特征,都非常相似,两个收益指数都具有厚尾分布现象。这种厚尾分布特征比较适合使用学生t分布函数来表现序列的概率分布特征。Ljung-Box统计量自相关性检验表明,在1%概率水平下,上证收益指数和深证收益指数各自都是具有自相关性的时间序列,适合建立AR自相关模型。ADF单位根检验表明,在1%概率水平下,上证收益指数和深证收益指数都是平稳时间序列变量,平稳时间序列变量适合建立协整模型。
对上证收益指数和深证收益指数之间相关性的实证分析,得到如下结果:
第一,Johansen-Juselius协整关系检验表明,上证收益指数和深证收益指数之间具有长期协整关系,它们之间的长期线性方程在1%概率水平下t检验显著有效。
第二,向量自回归(VAR)模型检验表明,上证收益指数与深证收益指数之间具有显著的长期双向Granger因果关系;向量误差修正(VECM)模型检验也表明,上证收益指数与深证收益指数之间具有显著的短期双向Granger因果关系。
第三,DCC动态条件相关系数不仅表现了上证收益指数与深证收益指数之间的动态相关性,对它的描述性统计分析也发现,DCC均值为0.9353,最小值为0.8345,最大值为1,说明上证收益指数与深证收益指数之间具有很高的相关性。
第四,Copula联合分布分析发现,学生t分布比Gaussian正态分布更适合反映上证收益指数与深证收益指数各自的分布特征;在学生t分布情况下,Clayton Copula下尾分布概率值达到0.986292,Gumbel Copula上尾分布概率值达到0.980082,说明上证收益指数与深证收益指数之间,既存在显著的上尾依赖关系,也存在显著的下尾依赖关系。
需要说明的是,上证综合指数成份股由在上海证券市场上市的所有股票组成,深圳成份指数成份股由在深圳证券市场上市的500只代表性股票组成,二者的构成不同,而且,深圳成份股在2015年5月20日之前只有40只在深圳证券市场上市的代表性股票,尽管如此,由于本文使用了收益指数进行分析,而没有直接使用价格指数进行分析,所以,基本可以忽略二者成份股构成不同所造成的差异,基于这个理由,本文没有讨论这一问题,以后将放在其它文章中讨论。
文章引用
阎可佳. 对沪深收益指数之间动态条件相关性的实证分析
An Empirical Analysis on the Dynamic Conditional Correlations between the Both Return Indices of Shanghai Stock Exchange and Shenzhen Stock Exchange[J]. 金融, 2017, 07(03): 126-143. http://dx.doi.org/10.12677/FIN.2017.73015
参考文献 (References)
- 1. 董彬彬. 中国沪深股市相关性研究[J]. 市场周刊: 理论研究, 2010(1): 61-63.
- 2. 刘喜波, 王增, 谷艳华. 基于Copula模型的沪深股市日收益率的相关性研究[J]. 数学的实践与认识, 2015, 45 (11): 101-108.
- 3. 陈梦龙. 中国股票市场的非对称相关性——基于AG-DCC-MGARCH模型的实证分析[J]. 区域金融研究, 2016 (9): 41-48.
- 4. 卢俊香, 武宇, 杜艳丽. 基于Copula的沪深股市相依结构与相关模式研究[J]. 四川理工学院学报(自然科学版), 2016, 29(2): 70-74.
- 5. 余平, 钟波. 基于Copula函数的沪深股市相关性研究[J]. 山西师范大学学报(自然科学版), 2007, 21(3): 28-32.
- 6. 闫海梅, 王波. 沪深300指数与沪深股市尾部相关性分析[J]. 数学的实践与认识, 2010, 40(22): 50-55.
- 7. 毕付宽. 基于非参数核密度估计时变相关Copula的沪深股市相关性研究[J]. 时代金融, 2015(10): 25-32.
- 8. 吴鑫育, 李心丹. 中国股市量价尾部相关性研究——基于随机Copula模型的实证[J]. 金融理论与实践, 2017(1): 93-97.
- 9. 吴栩, 宋光辉, 董艳. 沪深股市夏普比率的多重分形相关性分析[J]. 经济数学, 2014(2): 9-14.
- 10. Jorion, P. (2007) Value at Risk: The New Benchmark for Managing Financial Risk. McGraw-Hill, New York.
- 11. Alexander, C. (2008) Market Risk Analysis I: Quantitative Methods in Finance. John Wiley & Sons Ltd., Chichester.
- 12. Box, G.E.P. and Pierce, D.A. (1970) Distribution of Residual Correlations in Autoregressive-Integrated Moving Average Time Series Models. Journal of the American Statistical Association, 65, 1509-1526. https://doi.org/10.1080/01621459.1970.10481180
- 13. Ljung, G. and Box, G.E.P. (1978) On a Measure of Lack of Fit in Time Series Models. Biometrika, 66, 67-72. https://doi.org/10.1093/biomet/65.2.297
- 14. Tsay, R.S. (2005) Analysis of Financial Times Series. 2nd Edition, John Wiley & Sons, Inc., Hoboken. https://doi.org/10.1002/0471746193
- 15. Dickey, D.A. and Fuller, W.A. (1979) Distribution of the Estimators for Time Series with a Unit Root. Journal of the American Statistical Association, 74, 427-431. https://doi.org/10.1080/01621459.1979.10482531
- 16. Dickey, D.A. and Fuller, W.A. (1981) Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica, 49, 1057-1072. https://doi.org/10.2307/1912517
- 17. Jeffrey, M.W. (2000) Introductory Econometrics: A Modern Approach. South Western College.
- 18. Li, Z.N. and Ye, A.Z. (2000) High Econometrics. Tsinghua University Press, Beijing.
- 19. Granger, C.W.J. (1980) Testing for Causality: A Personal Viewpoint. Journal of Economic Dynamics and Control, 2, 329-352.
- 20. Davidson, R. and Mackinnon, J.G. (1993) Estimation and Inference in Econometrics. Oxford University Press, New York.
- 21. Johansen, S. (1988) Statistical Analysis of Cointegration Vectors. Journal of Economic Dynamics and Control, 12, 231-254.
- 22. Johansen, S. and Juselius, K. (1990) Maximum Likelihood Estimation and Inference on Cointegration with Application to the Demand for Money. Oxford Bulletin of Economics and Statistics, 52, 169-210. https://doi.org/10.1111/j.1468-0084.1990.mp52002003.x
- 23. Engle, R.F. and Granger, C.W.J. (1987) Cointegration and Error Correction: Representation, Estimation, and Testing. Econometrica, 55, 251-276. https://doi.org/10.2307/1913236
- 24. Liew, V.K. (2004) Which Lag Length Selection Criteria Should We Employ? Economic Bulletin, 3, 1-9.
- 25. Engle, R. (2002) Dynamic Conditional Correlation—A Simple Class of Multivariate GARCH Models. Journal of Business and Economic Statistics, 20, 339-350. https://doi.org/10.1198/073500102288618487
- 26. Sklar, A. (1973) Random Variables, Distribution Functions, and Copula. Kybernetica, 9, 449-460.
- 27. Clayton, D.G. (1978) A Model for Association in Bivariate Life Tables and Its Application in Epidemiological Studies of Familial Tendency in Chronic Disease Incidence. Biometrika, 65, 141-152. https://doi.org/10.1093/biomet/65.1.141
- 28. Gumbel, E.J. (1960) Bivariate Exponential Distributions. Journal of the American Statistical Association, 55, 698-707. https://doi.org/10.1080/01621459.1960.10483368
