Pure Mathematics
Vol.05 No.03(2015), Article ID:15260,4
pages
10.12677/PM.2015.53016
The Quenching Solutions of Parabolic Problems with Reaction Terms of Nonlocal and Nonlinear Type
Xiangcheng Zheng, Quangang Hou, Hao Yang
College of Science, China University of Petroleum, Qingdao Shandong
Email: 1393866052@qq.com
Received: May 1st, 2015; accepted: May 18th, 2015; published: May 21st, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study quenching problems for solutions of parabolic problems with reaction terms of nonlocal and nonlinear type. Setting some assumptions to the initial data, we acquire the criterion of whether or not the solutions will quench and we prove the quenching rates and quenching collection.
Keywords:Nonlocal Parabolic Equation, Quenching Solution, Quenching Rate, Quenching Collection
具非局部非线性项的抛物方程的熄灭解
郑祥成,侯全刚,杨昊
中国石油大学(华东)理学院,山东 青岛
Email: 1393866052@qq.com
收稿日期:2015年5月1日;录用日期:2015年5月18日;发布日期:2015年5月21日

摘 要
本文研究了一类具有非局部非线性项的抛物方程问题解的熄灭性质,在一定对初值的假设条件下,得到了解发生熄灭的判据,进而我们证得了解的熄灭速率和熄灭集合。
关键词 :非局部抛物方程,熄灭解,熄灭速率,熄灭集

1. 引言
本文主要研究了如下非局部抛物方程:
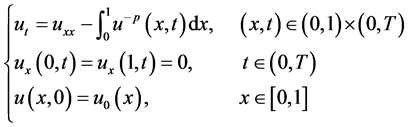 (1.1)
(1.1)
其中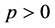 ,我们对初值作如下假设:
,我们对初值作如下假设:
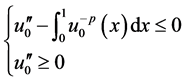 (1.2)
(1.2)
Kawarada [1] 于1975年首次提出熄灭(quenching)问题,并对如下非线性热方程进行了研究:
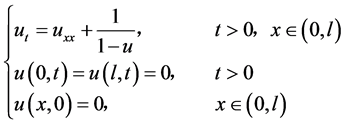
他指出若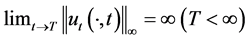 ,使得则称
,使得则称 在有限时刻熄灭,
在有限时刻熄灭,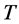 即称作古典解的最大存在时间。之后许多学者大力研究熄灭的性质,得到了很多模型的解熄灭的条件及解在熄灭时刻的渐近性质 [2] - [5] 。
即称作古典解的最大存在时间。之后许多学者大力研究熄灭的性质,得到了很多模型的解熄灭的条件及解在熄灭时刻的渐近性质 [2] - [5] 。
Pablo,Quiros和Rossi [4] 研究了带有Neumann边界条件的抛物系统:
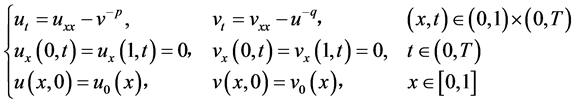
其中常数 。在这里,熄灭定义为:对于所有
。在这里,熄灭定义为:对于所有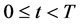 ,正的古典解
,正的古典解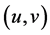 满足
满足

另外,熄灭也可以被定义为解在有限时刻发生某种导数的爆破。不同时熄灭现象是指解的一个分量在有限时刻熄灭,而另一个分量在该时刻之前保持恒正。
在假定初值的条件下,他们得到了非常完美的结果:若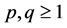 ,则解总是发生同时熄灭的;若
,则解总是发生同时熄灭的;若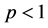 或
或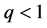 ,则存在初值,使得不同时熄灭现象发生;若
,则存在初值,使得不同时熄灭现象发生;若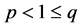 或
或 ,则解总是不同时熄灭。
,则解总是不同时熄灭。
Ferreira,Pablo,Quiros [2] 等人研究了边界流耦合的热方程组的不同时熄灭现象:
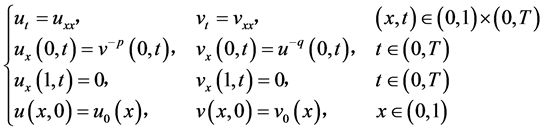
他们得到了:
1) 若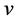 不发生熄灭,则
不发生熄灭,则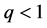 ;反之,若
;反之,若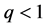 ,则对于任意初值
,则对于任意初值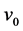 都存在初值
都存在初值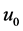 使得只有分量
使得只有分量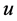 发生熄灭,而
发生熄灭,而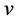 不发生熄灭。
不发生熄灭。
2) 若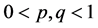 ,则存在初值,使得同时熄灭发生。
,则存在初值,使得同时熄灭发生。
3) 若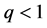 且
且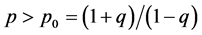 ,则解总是发生不同时熄灭的。
,则解总是发生不同时熄灭的。
他们还得到了熄灭速率和熄灭集等结果。
众所周知,系统(1.1)是一类非常重要的问题,局部存在性和比较原理非常容易证明,本文主要研究的是非线性抛物方程解的熄灭情况,这些是值得广泛关注的问题。
2. 主要结果
引理1。由系统(1.1)和初值的假设可知: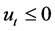 ,
,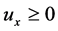 。
。
证明:这里引入比较原理 [6] :
设 在
在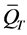 有界,
有界,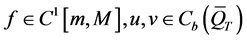 ,且当
,且当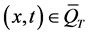 时
时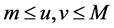 。如果
。如果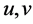 满足
满足
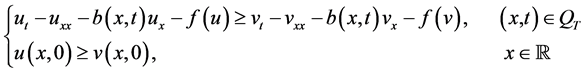
则 ,
, 。其中
。其中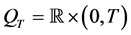 ,
,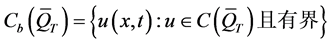 。
。
将(1.1)对 求导并由初值的假设可得
求导并由初值的假设可得
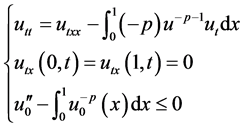
令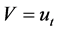 可得
可得
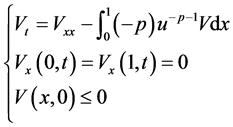 (1.3)
(1.3)
其中(1.3)最后一项利用了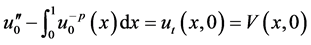 。
。
在比较原理中,令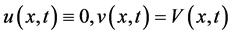 ,由(1.3)运用比较原理可得
,由(1.3)运用比较原理可得 ,即
,即
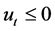 , 因为
, 因为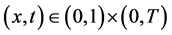 (1.4)
(1.4)
将(1.1)对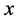 求导可得
求导可得
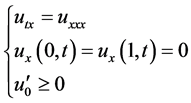
其中最后一个不等式利用了对初值的假设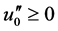 和
和 。
。
令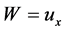 可得
可得
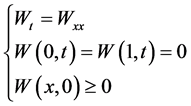 (1.5)
(1.5)
在比较原理中,令 ,由(1.5)运用比较原理可得
,由(1.5)运用比较原理可得 ,即
,即
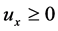 ,因为
,因为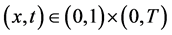 (1.6)
(1.6)
定理1。当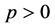 时,
时,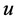 熄灭。
熄灭。
证明: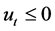 ,能得到
,能得到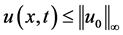 。对方程积分可得:
。对方程积分可得:
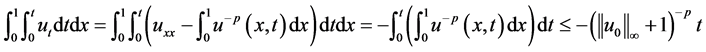 (1.7)
(1.7)
上式利用了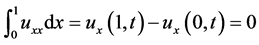 。
。
利用(1.7)的结论有
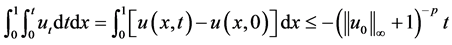
即
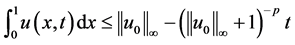 (1.8)
(1.8)
由(1.8)可知,若不等式左端是有界的,而右端随着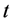 的增加将趋于
的增加将趋于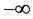 ,这显然是矛盾的,原因在于(1.7)左端积分中的
,这显然是矛盾的,原因在于(1.7)左端积分中的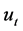 在某处是趋于
在某处是趋于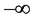 的,所以当
的,所以当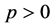 时,
时,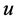 肯定熄灭。
肯定熄灭。
定理2。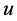 仅在
仅在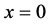 点熄灭。
点熄灭。
证明:令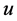 为熄灭解,由热方程的无限传播性,可知
为熄灭解,由热方程的无限传播性,可知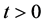 ,
,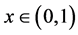 时,
时, 。
。
对于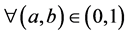 ,由
,由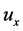 连续性可知,存在常数
连续性可知,存在常数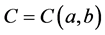 使得
使得 ,
,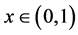 时,
时, 。对
。对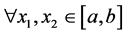 ,不妨设
,不妨设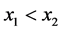 ,由
,由
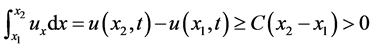
可知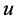 不可能在
不可能在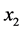 处趋于0,即不可能在
处趋于0,即不可能在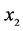 处熄灭。由
处熄灭。由 的任意性可知
的任意性可知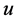 在
在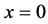 或在
或在 处熄灭,但由
处熄灭,但由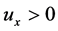 所以
所以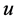 仅在
仅在 处熄灭。
处熄灭。
定理3。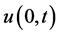 的上界估计为:
的上界估计为: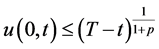
证明:由(1.6)可知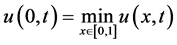 ,由
,由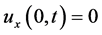 和(1.6)的结论可得
和(1.6)的结论可得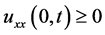 ,故
,故
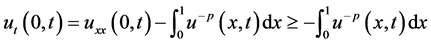
由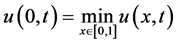 进一步可以得到
进一步可以得到
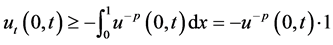
即
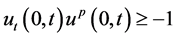
对上式积分得
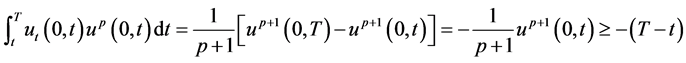 (1.9)
(1.9)
其中利用了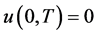 的熄灭性质。整理(1.9)右端的不等式可得
的熄灭性质。整理(1.9)右端的不等式可得
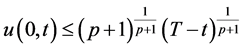
我们得到了 的上界估计。
的上界估计。
致谢
衷心感谢审稿人和编辑老师的指导和帮助,同时感谢指导老师刘丙辰的帮助。
基金项目
大学生创新创业训练计划项目(No. 20141283)。
文章引用
郑祥成,侯全刚,杨 昊, (2015) 具非局部非线性项的抛物方程的熄灭解
The Quenching Solutions of Parabolic Problems with Reaction Terms of Nonlocal and Nonlinear Type. 理论数学,03,100-104. doi: 10.12677/PM.2015.53016
参考文献 (References)
- 1. Kawarada, H. (1975) On solutions of initial-boundary problem . Publications of the Research Institute for Mathematical Sciences, 10, 729-736.
- 2. Ferreira, R., Pablo, A., Quiros, F., et al. (2006) Non-simultaneous quenching in a system of heat equations coupled at the boundary. Zeitschrift für Angewandte Mathematik und Physik ZAMP, 57, 586-594.
- 3. Levine, H.A. (1985) The phenomenon of quenching: A survey. In: Lakshmikantham, V., Ed., Trends in the Theory and Practice of Nonlinear Analysis, Elsevier Science, North Holland, 275-286.
- 4. de Pablo, A., Quiros, F. and Rossi, J.D. (2002) Nonsimltaneous quenching. Applied Mathematics Letters, 13, 265-269.
- 5. Zhou, J., He, Y. and Mu, C.L. (2008) Imcomplete quenching of heat equations with absorption. Applicable Analysis, 87, 523-529.
- 6. 叶其孝, 李正元, 王明新, 吴雅萍 (2013) 反应扩散方程引论. 科学出版社, 北京.