Pure Mathematics
Vol.05 No.06(2015), Article ID:16351,6
pages
10.12677/PM.2015.56038
Stability in Predator-Prey Model with Age-Structure
Huantao Zhu
Hunan College of Information, Changsha Hunan
Received: Oct. 26th, 2015; accepted: Nov. 10th, 2015; published: Nov. 17th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The stability in predator-prey model with age-structure is investigated. Sufficient conditions for global asymptotic stability of boundary equilibrium and positive invariance and the boundedness are derived.
Keywords:Age-Structure, Predator Model, Stability

一类具年龄结构的捕食–食饵模型的稳定性
朱焕桃
湖南信息职业技术学院,湖南 长沙

收稿日期:2015年10月26日;录用日期:2015年11月10日;发布日期:2015年11月17日

摘 要
研究了一类具有年龄结构的捕食–食饵模型系统,得到了该系统解的正不变性、有界性及其边界平衡点全局渐近稳定的充分条件。
关键词 :年龄结构,捕食模型,稳定性

1. 引言与引理
在现实生活中,各种种群的发展都与其年龄因素有着重要的关系,这表现在不同年龄的种群在生育和死亡方面存在很多差异。1911年,Sharpe和Lotka [1] 首次将种群的年龄因素考虑到模型中。随后,具有年龄结构的种群模型的研究有了丰富的结果[2] -[6] 。本文将考虑在经典的Lotka-Volterra捕食–食饵模型的基础上将年龄结构引入到捕食种群中且适合Mckendrick-Foerster方程的一类捕食–食饵模型:
 (1)
(1)
满足初始条件
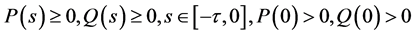 (2)
(2)
其中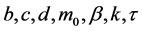 是正常数。
是正常数。
由文献[7] 知,系统(1)在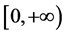 存在唯一解。
存在唯一解。
引理1.1 (Liapunov-LaSalle不变原理):若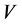 是
是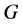 上的李雅普诺夫泛函,且
上的李雅普诺夫泛函,且 是方程
是方程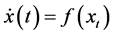 停留在
停留在 中的有界解,则当
中的有界解,则当 时,
时,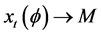 。其中
。其中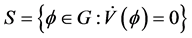 ,
,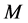 是集合
是集合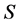 关于
关于 的最大不变集。
的最大不变集。
2. 主要结论
我们首先讨论系统(1)在满足初始条件(2)时的解是正的和有界的。
定理2.1:对一切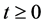 ,系统(1)满足初始条件(2)的解是正的。
,系统(1)满足初始条件(2)的解是正的。
证明:由系统(1)的第二个方程可以得到
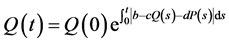
根据初始条件(2)可知,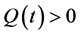 。
。
假设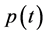 不恒为正,则一定存在一个
不恒为正,则一定存在一个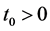 ,使得
,使得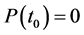 。
。
由(2)的第一个方程可得,
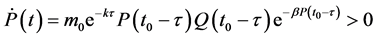
这说明对于充分小的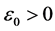 ,当
,当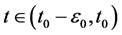 时,
时, ,于是产生矛盾。因此,
,于是产生矛盾。因此,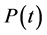 总是恒为正。
总是恒为正。
定理2.2:对一切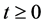 ,系统(1)满足初始条件(2)的解是有界的。
,系统(1)满足初始条件(2)的解是有界的。
证明:由(1)的第二个方程,我们可以得到

故对充分小的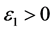 ,存在
,存在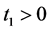 使得对所有的
使得对所有的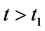 有
有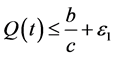
又根据系统(1)的第一个方程和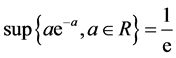 ,我们得到
,我们得到
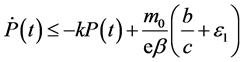
故对所有的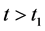 ,有
,有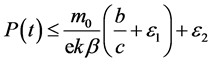 。
。
定理2.3:对于系统(1)的所有解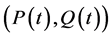 ,
,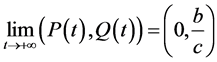 当且仅当
当且仅当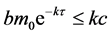 。
。
证明:先证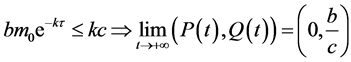 。
。
当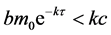 时,则存在充分小的
时,则存在充分小的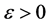 ,使得
,使得 ,根据定理2.1知,存在
,根据定理2.1知,存在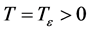 ,使得当
,使得当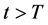 时,有
时,有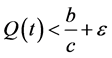 成立,从而对
成立,从而对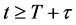 有
有
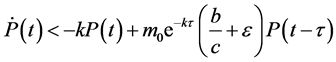
考虑比较方程
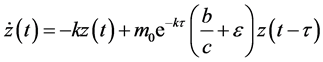
由文献[8] 中的引理1知,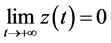 .又由定理2.1和比较定理得到
.又由定理2.1和比较定理得到
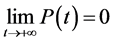
因此存在充分小的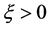 和
和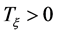 使得对所有的
使得对所有的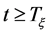 有
有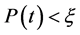 。
。
又由系统(1)的第二个方程有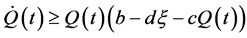 。
。
再由比较定理可得
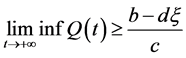 .
.
由于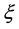 任意小,结合上面的讨论,我们有
任意小,结合上面的讨论,我们有 。
。
当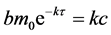 时,由系统(1)的第二个方程可知,当
时,由系统(1)的第二个方程可知,当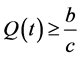 时它总递减。若存在
时它总递减。若存在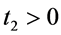 ,使得
,使得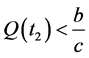 ,则对所有的
,则对所有的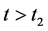 ,有
,有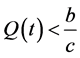 。事实上,若存在
。事实上,若存在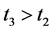 ,使得
,使得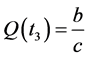 ,则有
,则有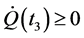 ,矛盾,故
,矛盾,故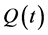 有两种情形;
有两种情形;
(1)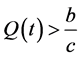 且
且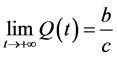 ;
;
(2) 存在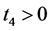 使得对所有的
使得对所有的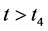 ,有
,有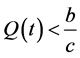 。
。
对情形(1),仅需证明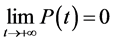 。对系统(1)的第二个方程两边从0到
。对系统(1)的第二个方程两边从0到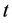 积分得
积分得
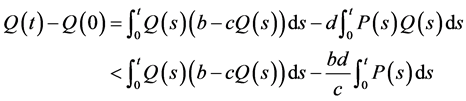
因此
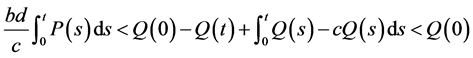
由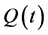 的有界性可得
的有界性可得 。
。
对情形(2),考虑Liapunov泛函
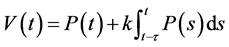 .
.
对所有的 沿着系统(1)的轨线计算
沿着系统(1)的轨线计算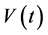 的导数可得
的导数可得
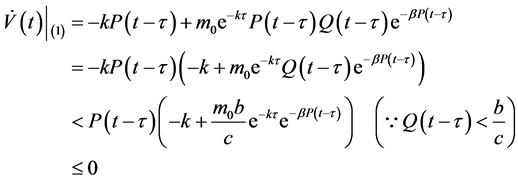
由引理1.1知,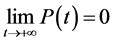 。对于
。对于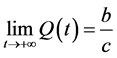 的证明类似于第一种情形。
的证明类似于第一种情形。
下证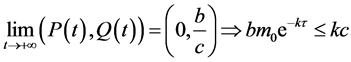 。否则,设
。否则,设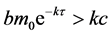 成立,则我们知道系统(1)有唯一的正平衡点
成立,则我们知道系统(1)有唯一的正平衡点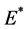 。这与系统(1)对所有解
。这与系统(1)对所有解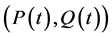 ,都有
,都有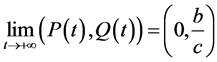 矛盾。
矛盾。
将系统(1)关于平衡点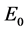 线性化,其相应的特征方程为
线性化,其相应的特征方程为
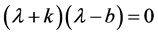
其根为 和
和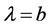 。这说明对所有的
。这说明对所有的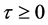 平衡点
平衡点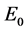 是不稳定的。
是不稳定的。
将系统(1)关于平衡点 线性化,相应的特征方程为
线性化,相应的特征方程为
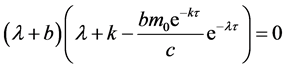
显然, 是上方程的一个特征根。因此,我们只需讨论下面方程的根
是上方程的一个特征根。因此,我们只需讨论下面方程的根
 (3)
(3)
令
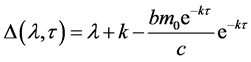
对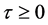 和
和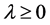 ,我们有
,我们有
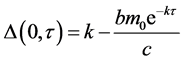 (4)
(4)
和
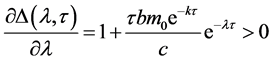 (5)
(5)
由式(4)知,当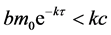 时,
时,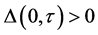 。再由式(5)知,对所有的
。再由式(5)知,对所有的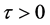 ,方程(3)没有正根。
,方程(3)没有正根。
注意到若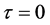 和
和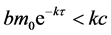 ,则方程(3)的特征根是负的。进一步我们可以证明当
,则方程(3)的特征根是负的。进一步我们可以证明当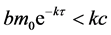 时,对所有的
时,对所有的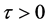 ,方程(3)的所有根必定具有负实部。假设存在
,方程(3)的所有根必定具有负实部。假设存在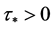 使得方程(3)有一对纯虚根
使得方程(3)有一对纯虚根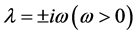 ,则由方程(3),我们有
,则由方程(3),我们有

两边平方相加可得
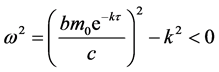
这说明方程(3)没有正根,即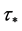 不存在。因此,当
不存在。因此,当 时,方程(3)的所有根都具有负实部,即系统(1)的平衡点
时,方程(3)的所有根都具有负实部,即系统(1)的平衡点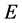 渐进稳定的。
渐进稳定的。
当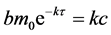 时,
时,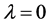 是方程(3)的特征根。由式(5)知,
是方程(3)的特征根。由式(5)知,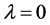 是一个简单的特征根。
是一个简单的特征根。
当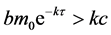 时,由式(4)知
时,由式(4)知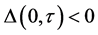 ,而
,而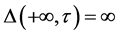 ,因此
,因此 至少有一个正实根,从而平衡点
至少有一个正实根,从而平衡点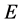 是不稳定的。
是不稳定的。
由上述讨论和定理2.3,我们得到以下结论
定理2.4:当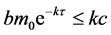 时,系统(1)的平衡点
时,系统(1)的平衡点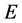 是全局渐进稳定的。
是全局渐进稳定的。
3. 举例
我们考虑如下系统
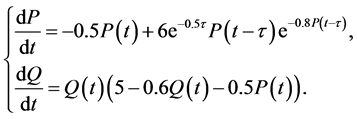 (6)
(6)
通过计算,当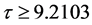 时,我们得到
时,我们得到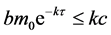 ,其中
,其中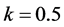 ,
,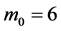 ,
,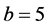 ,
,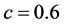 。根据定理2.4,系统(6)的平衡点是全局渐进稳定的。
。根据定理2.4,系统(6)的平衡点是全局渐进稳定的。
基金项目
湖南省教育厅资助科研项目(13C660)。
文章引用
朱焕桃. 一类具年龄结构的捕食–食饵模型的稳定性
Stability in Predator-Prey Model with Age-Structure[J]. 理论数学, 2015, 05(06): 266-271. http://dx.doi.org/10.12677/PM.2015.56038
参考文献 (References)
- 1. Sharpe, F.R. and Lotka, A.J. (1911) A Problem in Age Distribution. Philosophical Magazine, 21, 435-438. http://dx.doi.org/10.1080/14786440408637050
- 2. Cushing, J.M. (1976) Periodic Lotka-Volterra Competition Equations. Journal of Mathematical Biology, 30, 665-673.
- 3. Webb, G.F. (1985) Theory of Nonlinear Age-Dependent Population Dynamics. Marcel Dekker, New York.
- 4. Cushing, J.M. and Saleem, M. (1982) A Predator-Prey Model with Age Structure. Journal of Mathematical Biology, 14, 231-250. http://dx.doi.org/10.1007/BF01832847
- 5. Anderson, R.M. and May, R.M. (1991) Infectious Diseases of Hu-mans: Dynamics and Control. Oxford University Press, Oxford.
- 6. 马知恩. 种群动态学数学建模与研究[M]. 合肥: 安徽教育出版社, 1984.
- 7. Hale, J.K. and Lunel, S.M.V. (1993) Introduction to Functional Differential Equa-tions. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-1-4612-4342-7
- 8. Gourley, S.A. and Kuang, Y. (2004) A Stage Structured Pre-dator-Prey Model and Its Dependence on Maturation Delay and Death Rate. Journal of Mathematical Biology, 49, 188-200. http://dx.doi.org/10.1007/s00285-004-0278-2