Pure Mathematics
Vol.06 No.02(2016), Article ID:17142,8
pages
10.12677/PM.2016.62015
The Lelong Number of a 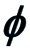 -Positive Closed Current on
-Positive Closed Current on 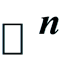
Fang Wang, Qianqian Kang
College of Science and Technology, Zhejiang International Studies University, Hangzhou Zhejiang
Received: Feb. 28th, 2016; accepted: Mar. 11th, 2016; published: Mar. 17th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we give the Lelong number of a 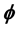 -positive closed current
-positive closed current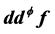 , where
, where 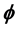 is the special Lagrangian calibration and f is a
is the special Lagrangian calibration and f is a 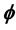 -plurisubharmonic function in
-plurisubharmonic function in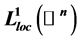 . Using that Lelong number, we generalize the minimum modulus principle for the holomorphic function of one complex variable, and we get an estimate of the low bound for
. Using that Lelong number, we generalize the minimum modulus principle for the holomorphic function of one complex variable, and we get an estimate of the low bound for 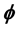 -plurisubharmonic functions.
-plurisubharmonic functions.
Keywords:Lelong Number, Special Lagrangian Calibration, 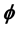 -Plurisubharmonic Function,
-Plurisubharmonic Function, 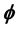 -Positive Closed Current
-Positive Closed Current

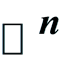 上
上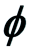 -闭正流的Lelong数
-闭正流的Lelong数
王芳,康倩倩
浙江外国语学院科学技术学院,浙江 杭州
收稿日期:2016年2月28日;录用日期:2016年3月11日;发布日期:2016年3月17日

摘 要
本文给出了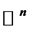 上
上 -闭正流
-闭正流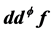 的Lelong数,这里
的Lelong数,这里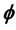 是特殊Lagrangian calibration,f是
是特殊Lagrangian calibration,f是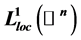 中的
中的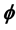 -多次下调和函数。并且我们应用此Lelong数,将单复变中全纯函数的极小模原理进行了推广,给出了此类
-多次下调和函数。并且我们应用此Lelong数,将单复变中全纯函数的极小模原理进行了推广,给出了此类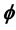 -多次下调和函数的一个下界估计。
-多次下调和函数的一个下界估计。
关键词 :Lelong数,特殊Lagrangian calibration,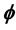 -多次下调和函数,
-多次下调和函数,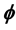 -闭正流
-闭正流

1. 引言及主要结果
在 [1] - [4] 中,Harvey及Lawson介绍了一些具体的calibrations,以及calibrated几何中的多次下调和函数,闭正流等。这些闭正流是经典的复几何中相应概念的推广,并且拥有一些重要性质。本文给出了一个特殊Lagrangian calibration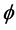 所对应的
所对应的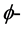 闭正流,并给出它的Lelong数的具体表达式。应用此Lelong数,给出
闭正流,并给出它的Lelong数的具体表达式。应用此Lelong数,给出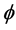 -多次下调和函数的一个下界估计。
-多次下调和函数的一个下界估计。
首先给出 [1] [3] 中的一些定义。如果黎曼流形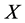 上的一个闭的
上的一个闭的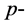 形式
形式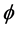 ,对
,对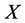 上的所有的单位简单切
上的所有的单位简单切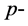 向量
向量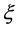 ,都有
,都有
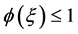
则称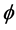 为一个calibration。一个单位简单切
为一个calibration。一个单位简单切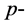 向量
向量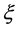 ,如果满足
,如果满足
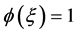
则称此 为一个
为一个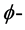 平面。令
平面。令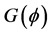 表示
表示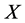 上
上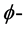 平面的全体。如果一个calibration
平面的全体。如果一个calibration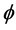 的共变导数为0,则称
的共变导数为0,则称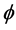 是平行的。在 [2] 中,Harvey及Lawson给出了一般的calibration
是平行的。在 [2] 中,Harvey及Lawson给出了一般的calibration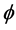 对应的
对应的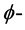 多次下调和函数及
多次下调和函数及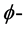 闭正流。但本文只讨论平行的calibration。下面给出相应的定义。令
闭正流。但本文只讨论平行的calibration。下面给出相应的定义。令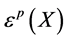 表示
表示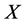 上
上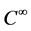 的
的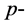 形式。对
形式。对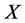 上任何光滑函数f,算子
上任何光滑函数f,算子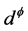 定义为:
定义为:
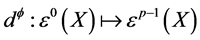
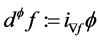
其中,i表示对微分形式的内乘,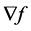 是f在
是f在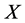 中的梯度。因此,算子
中的梯度。因此,算子
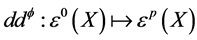
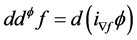
这里,对一个平行的calibration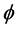 及一个光滑函数f,如果对每个
及一个光滑函数f,如果对每个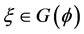 ,有
,有
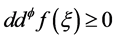
则称f是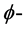 多次下调和函数。
多次下调和函数。
令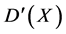 表示X上的所有光滑函数构成的空间的对偶。如果一个分布
表示X上的所有光滑函数构成的空间的对偶。如果一个分布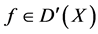 满足对所有的光滑截面
满足对所有的光滑截面 及光滑的具有紧支柱非负函数λ,有
及光滑的具有紧支柱非负函数λ,有
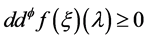
则称此分布f是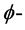 多次下调和的。容易证明,当f是
多次下调和的。容易证明,当f是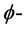 多次下调和函数时,这两个定义是等价的。用
多次下调和函数时,这两个定义是等价的。用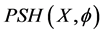 表示x上所有的
表示x上所有的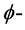 多次下调和函数及
多次下调和函数及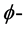 多次下调和分布。
多次下调和分布。
令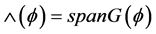 。
。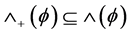 表示顶点在原点,集合
表示顶点在原点,集合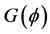 的凸锥。
的凸锥。
 。这里,
。这里, 表示黎曼流形X的余切空间。一个p维的流t,如果对所有具有紧支柱的p-形式
表示黎曼流形X的余切空间。一个p维的流t,如果对所有具有紧支柱的p-形式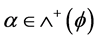 ,有
,有
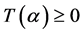
则称t是一个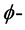 正流。如果还满足
正流。如果还满足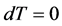 ,则称t是一个
,则称t是一个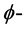 闭正流。关于流的定义,可以参考 [5] 的第104页。
闭正流。关于流的定义,可以参考 [5] 的第104页。
令 是
是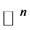 上的一个平行的calibration。t是一个p维的
上的一个平行的calibration。t是一个p维的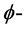 正流且
正流且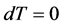 。给定一点a,如果极限
。给定一点a,如果极限

存在,则称此极限为t在点a处的Lelong数,记为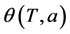 。这里
。这里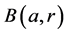 是
是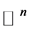 中球心为a,半径为r的闭球,
中球心为a,半径为r的闭球,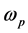 是
是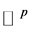 中单位球的体积,参考Demailly [6] 第18页及 [7] 中关于Lelong数的定义。
中单位球的体积,参考Demailly [6] 第18页及 [7] 中关于Lelong数的定义。
令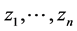 表示n维复欧氏空间
表示n维复欧氏空间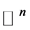 上点的坐标。闭的
上点的坐标。闭的 形式
形式
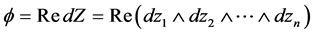
是一个平行的calibration,称为特殊Lagrangian calibration。在 [2] 中,附录:The reduced 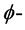 Hessian一节中的定理5.19,告诉我们,如果
Hessian一节中的定理5.19,告诉我们,如果 为特殊Lagrangian calibration,则
为特殊Lagrangian calibration,则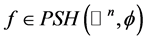 等价于
等价于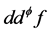 是一个
是一个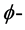 正流。显然,
正流。显然,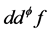 是闭的。对此闭正流,我们有下面的结论。
是闭的。对此闭正流,我们有下面的结论。
定理1.1:令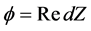 是
是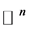 上的特殊Lagrangian calibration。
上的特殊Lagrangian calibration。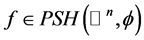 ,则
,则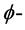 闭正流
闭正流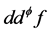 在点a处的Lelong数
在点a处的Lelong数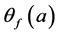 存在且
存在且
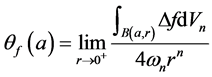
其中,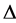 是
是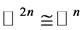 上的Laplace算子,
上的Laplace算子, 是
是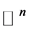 上的体积元。
上的体积元。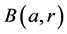 是
是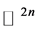 中球心为a,半径为r的开球,
中球心为a,半径为r的开球,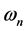 是
是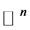 中单位球的体积。
中单位球的体积。
令
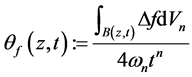 (1.1)
(1.1)
函数f在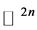 中一个开球B上的Riesz质量定义为:
中一个开球B上的Riesz质量定义为:
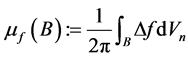 (1.2)
(1.2)
假设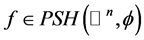 并且是上半连续的,那么可以证明f是下调和的。我们应用
并且是上半连续的,那么可以证明f是下调和的。我们应用 闭正流
闭正流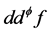 的Lelong数及下调和函数的Poisson-Jensen公式,得到了关于f的一个下界估计式。
的Lelong数及下调和函数的Poisson-Jensen公式,得到了关于f的一个下界估计式。
定理1.2:令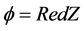 是
是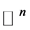 上的特殊Lagrangian calibration,这里,
上的特殊Lagrangian calibration,这里, 。f为
。f为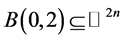 上的
上的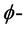 多次下调和函数,并且在
多次下调和函数,并且在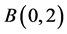 上是上半连续的,且有有界的Riesz质量
上是上半连续的,且有有界的Riesz质量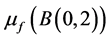 。那么对任何实数
。那么对任何实数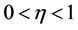 ,及
,及 ,存在可数个小球
,存在可数个小球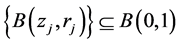 ,对
,对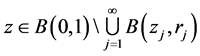 ,有
,有
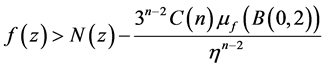 (1.3)
(1.3)
其中,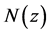 表示f在单位球
表示f在单位球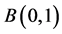 的边界上的最小值,
的边界上的最小值,
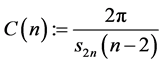
这些小球的半径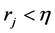 ,
,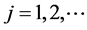 ,并且,
,并且,
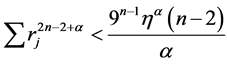 (1.4)
(1.4)
令
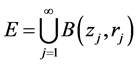 (1.5)
(1.5)
则e是一个Borel集,且满足
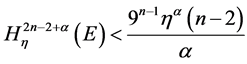
这里,一个集合e的p维的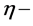 Hausdorff content
Hausdorff content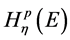 定义为
定义为
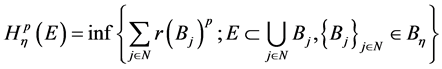 (1.6)
(1.6)
其中,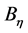 是指e的覆盖的全体,其中,每个覆盖是由可数个小球并起来,每个小球的半径
是指e的覆盖的全体,其中,每个覆盖是由可数个小球并起来,每个小球的半径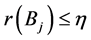 ,
,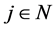 。
。
注:在 [8] 中,作者给出了极小模原理在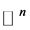 中的经典的多次下调和函数中的推广。
中的经典的多次下调和函数中的推广。
2.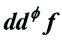 的Lelong数
的Lelong数
令 为
为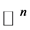 上一个平行的calibration且
上一个平行的calibration且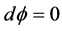 ,t为一个
,t为一个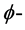 闭正流。在 [1] 中的第2.5节,Harvey及Lawson已经证明,
闭正流。在 [1] 中的第2.5节,Harvey及Lawson已经证明,

是关于变量r单调递增的函数,这里,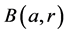 是
是 中球心为a,半径为r的闭球,
中球心为a,半径为r的闭球,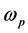 是
是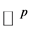 中单位球的体积。因此,
中单位球的体积。因此,
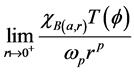
存在。
令 且f为
且f为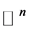 上一个光滑的
上一个光滑的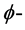 多次下调和函数,则我们有下面命题成立。
多次下调和函数,则我们有下面命题成立。
命题2.1:(参见 [9] ,命题2.1)
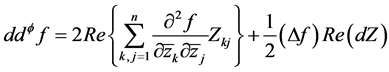
这里,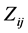 表示一个
表示一个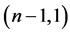 -形式,它是在
-形式,它是在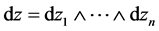 中,用
中,用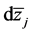 替代
替代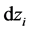 。
。
下面给出定理1.1的证明。
定理1.1的证明:令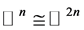 。
。 上的特殊Lagrangian calibration
上的特殊Lagrangian calibration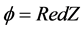 ,它是一个
,它是一个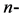 形式。令
形式。令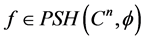 ,我们已经知道,
,我们已经知道,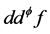 是一个n维的
是一个n维的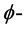 闭正流。令*表示Hodge星算子。当f为
闭正流。令*表示Hodge星算子。当f为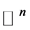 上光滑的
上光滑的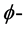 多次下调和函数,由命题2.1知,
多次下调和函数,由命题2.1知,
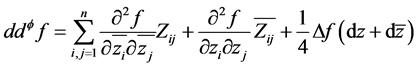
那么,
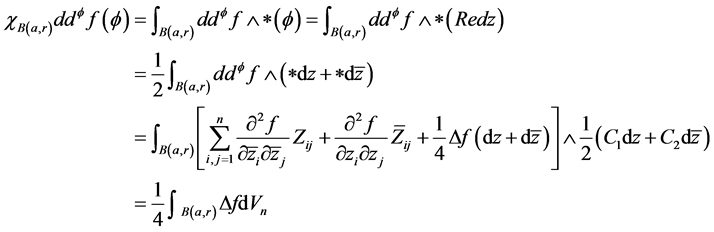 (2.1)
(2.1)
这里,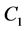 ,
, 都是常数,根据Hodge星算子的定义,它们分别满足
都是常数,根据Hodge星算子的定义,它们分别满足 ,
,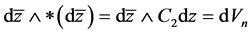 。由于
。由于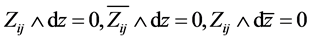 ,
,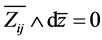 。
。
因此,(2.1)中最后一个等式成立。
如果f不是光滑的,我们可以先将f光滑化,即将f与光滑核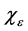 做卷积,记为
做卷积,记为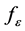 。那么,可以证明随着
。那么,可以证明随着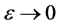 ,
,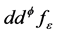 收敛到
收敛到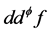 。现选取一个函数
。现选取一个函数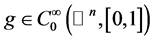 ,则有
,则有
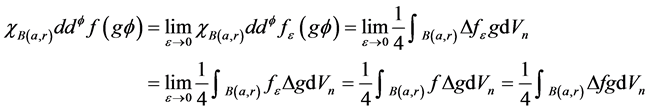
因此,当f为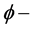 多次下调和分布时,也有
多次下调和分布时,也有
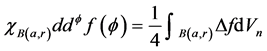
则有,
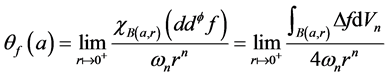
证毕。
3.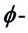 多次下调和函数的下界估计
多次下调和函数的下界估计
在 [8] 中,作者给出了极小模原理在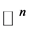 中的经典的多次下调和函数中的推广。本节参考 [8] 中的一些方法,给出了
中的经典的多次下调和函数中的推广。本节参考 [8] 中的一些方法,给出了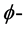 多次下调和函数的一个下界估计。
多次下调和函数的一个下界估计。
定理1.2的证明:因为f为定义在 上的
上的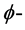 多次下调和函数,那么,对所有的
多次下调和函数,那么,对所有的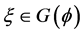 ,有
,有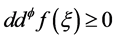 。
。
令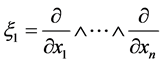 ,
, ,这里,
,这里,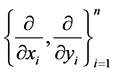 是切空间
是切空间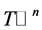 的一组基。则显然
的一组基。则显然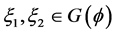 ,且
,且
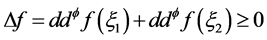 (3.1)
(3.1)
又因为f在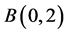 上是上半连续的,从而f在
上是上半连续的,从而f在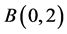 上是下调和的。由Poisson-Jensen公式(参考 [5] ,p. 138),对
上是下调和的。由Poisson-Jensen公式(参考 [5] ,p. 138),对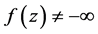 ,有
,有
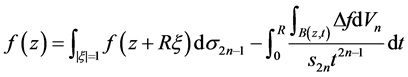
这里,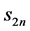 是
是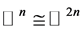 中单位球的表面积。再由Lelong数的定义(1.1)知,
中单位球的表面积。再由Lelong数的定义(1.1)知,
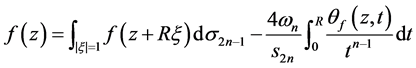 (3.2)
(3.2)
因为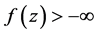 ,所以,
,所以,
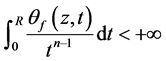 (3.3)
(3.3)
注意到,
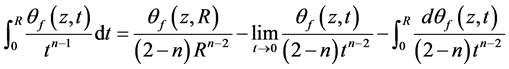
如果上式等号右边的第二项不为零,则由于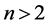 ,只能是
,只能是
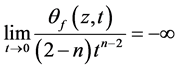
从而,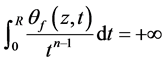 ,这与(3.3)矛盾,故
,这与(3.3)矛盾,故
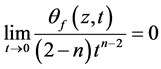 (3.4)
(3.4)
现在固定实数 及
及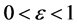 。任取实数
。任取实数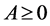 ,与t无关,但可以与
,与t无关,但可以与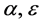 有关。
有关。
由(3.4)知,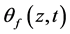 是
是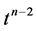 当
当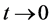 时的高阶无穷小量,故我们可以定义集合
时的高阶无穷小量,故我们可以定义集合
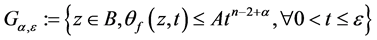 (3.5)
(3.5)
那么,对于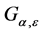 中的每一点,都有
中的每一点,都有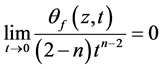 ,这意味着集合
,这意味着集合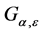 与f的极集
与f的极集 没有交点。
没有交点。
令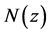 为
为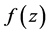 在
在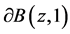 上的最小值。固定一点
上的最小值。固定一点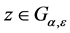 ,则
,则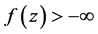 ,由(3.2)可得
,由(3.2)可得
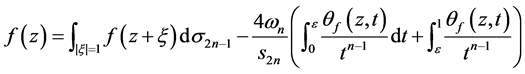
由于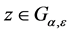 ,由(3.5)知,
,由(3.5)知, 从而
从而
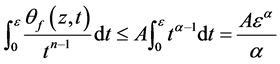 (3.6)
(3.6)
并且,由于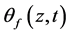 关于t是单调递增的及(1.1)知,对
关于t是单调递增的及(1.1)知,对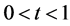 ,
, 。因此,
。因此,
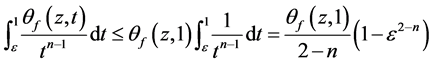 (3.7)
(3.7)
由(1.1)及(1.2)知,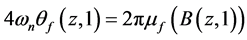 。由于,
。由于, ,故由(3.1)知,
,故由(3.1)知,
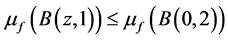 (3.8)
(3.8)
从而,由(3.2)得,
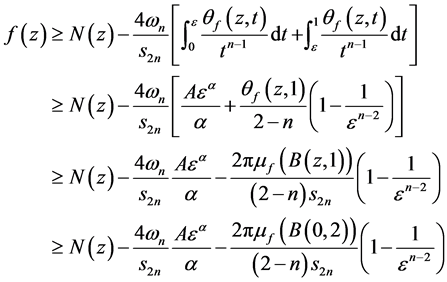
这里,第二,三,四个不等式分别由(3.6),(3.7),(3.8)所得。
取
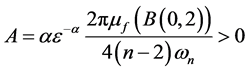 (3.9)
(3.9)
则有,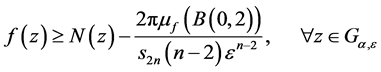 。
。
令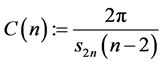 及
及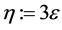 ,则公式(1.3)成立。
,则公式(1.3)成立。
令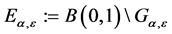 。由(3.5)知,对任意一点
。由(3.5)知,对任意一点 ,都会相应的存在一个实数
,都会相应的存在一个实数 ,满足
,满足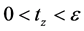 ,使得
,使得
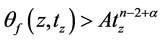 (3.10)
(3.10)
从而,由(1.1)及(1.2)知,
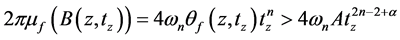
这些小球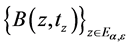 构成集合
构成集合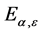 的一个覆盖,由Vitalli覆盖引理知,在
的一个覆盖,由Vitalli覆盖引理知,在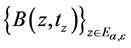 中,存在可数个互不相交的小球,记作
中,存在可数个互不相交的小球,记作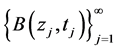 ,并且满足
,并且满足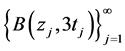 也能够覆盖集合
也能够覆盖集合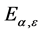 。并且,由(3.9)及(3.10)知,
。并且,由(3.9)及(3.10)知,
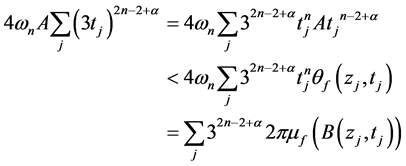
仍然取a为(3.9)中所定义的。由于
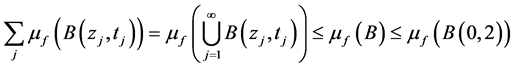
可得,
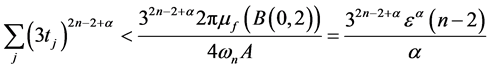
令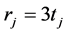 ,及
,及 ,可得,
,可得,

即(1.4)成立。故我们找到了可数个小球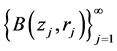 ,对
,对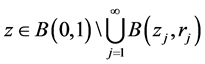 ,有(1.3)成立,而且这些小球的半径满足(1.4)。由(1.5)知,
,有(1.3)成立,而且这些小球的半径满足(1.4)。由(1.5)知, ,则(1.6)成立。
,则(1.6)成立。
证毕。
基金项目
浙江省教育厅基金(No. Y201328697),浙江省自然科学基金(No. LQ14A010003)。
文章引用
王 芳,康倩倩. Cn上φ-闭正流的Lelong数
The Lelong Number of a φ-Positive Closed Current on Cn[J]. 理论数学, 2016, 06(02): 103-110. http://dx.doi.org/10.12677/PM.2016.62015
参考文献 (References)
- 1. Harvey, R. and Lawson, H. (1982) Calibrated Geometries. Acta Mathematica, 148, 47-157. http://dx.doi.org/10.1007/BF02392726
- 2. Harvey, R. and Lawson, H. (1982) Plurisubharmonic Functions in Calibrated Geometries. http://arxiv.org/abs/math/0601484
- 3. Harvey, R. and Lawson, H. (2009) An Introduction to Potential Theory in Calibrated Geometry. American Journal of Mathematics, 131, 893-944. http://arxiv.org/abs/0710.3920
- 4. Harvey, R. and Lawson, H. (2009) Duality of Positive Currents and Pluri-subharmonic Functions in Calibrated Geometry. American Journal of Mathematics, 131, 1211-1240. http://arxiv.org/abs/0710.3921
- 5. Klimek, M. (1991) Pluripotential Theory. Clarendon Press, Oxford and New York.
- 6. Demailly, J. (2010) Analytic Methods in Algebraic Geometry. International Press, Some-rville.
- 7. Demailly, J. (1993) Monge-Ampere Operators, Lelong Numbers and Intersection Theory. Complex Analysis and Geometry. The University Series in Mathematics, Plenum, New York, 115-193.
- 8. Zeriahi, A. (2007) A Minimum Principle for Plurisubharmonic Functions. Indiana University Mathematics Journal, 56, 2671-2696. http://dx.doi.org/10.1512/iumj.2007.56.3209
- 9. Kang, Q.Q. (2015) A Monge-Ampere Type Operator in 2-Dimensional Special Lagrangian Geometry. Italian Journal of Pure and Applied Mathematics, 34, 449-462.