Modern Physics
Vol.07 No.04(2017), Article ID:21206,12
pages
10.12677/MP.2017.74011
Atomic Model and Experimental Analysis Based on Particle Spin
Xianjin Wu
School of Information and Mathematics, Yangtze University, Jingzhou Hubei

Received: June 12th, 2017; accepted: Jun. 26th, 2017; published: Jun. 30th, 2017

ABSTRACT
The atomic model is the foundation of atomic physics. In this paper, the principle of atomic nucleus interaction with electrons is discussed, and the atomic model based on particle spin is proposed by analysis of experimental particle spin. The nucleus outer gradient energy level, outer electron energy, basic charge and electromagnetic effect principle are described based on analysis of the Planck's constant and related experimental. The interaction between electron and photon and the principle of photoelectric effect are discussed based on the assumption of photon (elementary particle) rest mass constant. Finally, the relationship between hydrogen atom spectra and fine structure constants is discussed. This article discusses some basic problems of atomic model, will open up new ideas for the development of atomic physics, showing broad prospects for application of atomic physics.
Keywords:Particle Spin, Atomic Model, Basic Charge, Photon Rest Mass Constant
基于粒子自旋的原子模型与实验分析
吴先金
长江大学信息与数学学院,湖北 荆州
收稿日期:2017年6月12日;录用日期:2017年6月26日;发布日期:2017年6月30日

摘 要
原子模型是原子物理学的基础。本文通过粒子自旋实验分析,论述了原子核与电子相互作用原理,提出了基于粒子自旋的原子模型。基于对普朗克常数和相关实验分析,阐述了原子核外层梯度能级、外层电子能量、基本电荷及电磁效应原理。基于光子(基本粒子)静止质量常数假设,论述了电子与光子的相互作用及光电效应原理。最后,论述了氢原子光谱与精细结构常数的联系。本文对原子模型一些基本问题的讨论,将对原子物理学的发展开拓新的思路,对原子物理学的应用展示广阔的前景。
关键词 :粒子自旋,原子模型,基本电荷,光子静止质量常数

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
原子模型是原子物理学的基础,一个多世纪以来,许多物理学家进行了深入地实验与探索。19世纪初,约翰∙道尔顿认为原子是不可分割的一个整体。1897年,约翰∙汤姆森在阴极射线实验中发现原子中的电子,认为原子由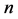 个带正电的颗粒和
个带正电的颗粒和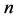 个带负电的电子组成,将原子描述为葡萄干蛋糕模型。1911年,欧内斯特∙卢瑟福分析阿尔法粒子入射金箔实验,发现带正电的原子核,认为电子绕核作轨道运动,称其为行星模型。1914年,尼尔斯∙波尔修改卢斯福原子模型,提出轨道电子可吸收或发射能量,每一根光谱线与电子的轨道跃迁相联系,称其为量子化原子模型。1924年,德布罗意在他的博士论文中提出实物粒子(如电子)具有波动性的概念,并用来描述轨道电子的波动性。1926年初,薛定谔提出微观粒子的波动力学方程,并用来解释氢原子光谱。1927年海森堡提出测不准原理,即微观粒子运动的位置和动能不能同时准确测定。
个带负电的电子组成,将原子描述为葡萄干蛋糕模型。1911年,欧内斯特∙卢瑟福分析阿尔法粒子入射金箔实验,发现带正电的原子核,认为电子绕核作轨道运动,称其为行星模型。1914年,尼尔斯∙波尔修改卢斯福原子模型,提出轨道电子可吸收或发射能量,每一根光谱线与电子的轨道跃迁相联系,称其为量子化原子模型。1924年,德布罗意在他的博士论文中提出实物粒子(如电子)具有波动性的概念,并用来描述轨道电子的波动性。1926年初,薛定谔提出微观粒子的波动力学方程,并用来解释氢原子光谱。1927年海森堡提出测不准原理,即微观粒子运动的位置和动能不能同时准确测定。
这些理论从不同方面揭示原子运动的现象,力求做到与相关实验相吻合。但是这些理论没有很好地研究原子核、电子、光子的性质和运动,以及三者之间的相互作用,没有很好地揭示原子运动的物理机制,不能很好地解释多电子原子及其运动。因而,原子理论的基础性作用及其应用都受到了极大限制。
由于篇幅有限,本文主要分析以下几个问题:1) 基于原子核、电子、光子自旋的原子模型及三者之间的关系;2) 基于普朗克常数的原子核外层梯度能级与外层电子能级原理;3) 基于光子静止质量常数的外层电子的光子吸收与辐射原理;4) 氢原子光谱与精细结构常数分析。
2. 基于粒子自旋的原子模型
自旋是基本粒子的内禀属性。所谓基本粒子自旋,是指有一定半径的基本粒子体围绕自己的轴心旋转,而且伴随一个旋转的磁场。这个磁场从里至外有一个磁场梯度,离磁场中心越远,磁密度越小,反之越大。基本粒子的自旋磁场符合右手自旋定则或左手自旋定则(即四指为自旋方向,大拇指为磁场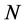 极方向)。一种基本粒子或具有右手自旋定则磁场,或具有左手自旋定则磁场,两者互为正反粒子,如正反质子、正反电子、正反光子等。到目前为止,很多物理实验证明基本粒子具有自旋并存在磁场,但不能检测到基本粒子围绕自己的轴心旋转。基本粒子总是处于运动状态,使基本粒子通过特定的磁场或能量场,可以观察它的行为和运动轨迹,进而测量基本粒子的自旋方向和自旋力度。
极方向)。一种基本粒子或具有右手自旋定则磁场,或具有左手自旋定则磁场,两者互为正反粒子,如正反质子、正反电子、正反光子等。到目前为止,很多物理实验证明基本粒子具有自旋并存在磁场,但不能检测到基本粒子围绕自己的轴心旋转。基本粒子总是处于运动状态,使基本粒子通过特定的磁场或能量场,可以观察它的行为和运动轨迹,进而测量基本粒子的自旋方向和自旋力度。
1925年,乌仑贝克(G.Uhlenbeck)和古兹米特(S.A.Goudsmit)在分析施特恩–格拉赫实验和反常塞曼效应等实验时,提出电子自旋假设。1928年狄拉克提出包含电子自旋的相对论波动方程。在量子力学中,基本粒子的自旋被解释成基本粒子运动的角动量。1940年泡利(Pauli)证明“自旋统计定理”,阐述了费米子具有半整数自旋,玻色子具有整数自旋。1995年,Kw1atet等人 [1] 采用Ⅱ型参量下转换产生极化纠缠光子对,当泵浦光打在BBO晶体上时,一个光子会被劈成两半,产生两个波长相等、出射角度与自旋态相关联的光子。
霍尔效应实际上是电子在进入外加磁场时,由于电子自旋有的向下有的向上而形成的。随着外加磁场的增强,导体两端的电势差会加大。早在1879年,Edwin H.Hall在非磁金属中发现正常霍尔效应 [2] 。将导体置于外磁场中,导体中的电流垂直于外磁场,在垂直于电流与磁场组成的平面方向上会出现横向电压。第二年,他又在3d磁性金属中发现反常霍尔效应 [3] 。Klausvon Klitzing在极低温和强磁场下发现半导体中的量子霍尔效应 [4] 。2003年,Murakamis、Nagaosa、Zhang [5] 以及Sinova [6] 等人发现一种在非磁金属中出现的纯自旋积累的霍尔效应。由于材料不存在对称破缺,自旋向上和自旋向下的载流子分别向材料两端偏移,并且数量相等,材料两端没有电荷的积累,只有自旋积累,从而形成了纯自旋流。2012年,
原子是由质子(中子)与电子构成的,原子的运行机制服从粒子自旋定则。将质子确定为左手自旋,则质子具有左手自旋磁场;电子为右手自旋,具有右手自旋磁场。粒子的自旋磁场,实际上是粒子的磁量子体,在不同的磁场环境中有不同的量子态。粒子的磁量子体,是源于核自旋的磁量子“自旋流体”,具有柔性,并非刚性。粒子磁量子体,由里至外,柔性增加;由外至里,刚性增强。粒子磁量子体的大小与粒子的质量呈正比,也与粒子的能量呈正比。粒子自旋磁场,符合同性相斥、异性相吸的原理。原子核是由质子与中子构成的,原子核的自旋磁场是质子自旋磁场的叠加态。原子核(质子)吸引电子,在一个元素中,质子数与电子数相等。当原子核吸引一个电子的时候,电子作为一个自旋磁场进入原子核的自旋磁场,电子的磁极与原子核的磁极相反,被原子核吸引;电子的自旋与原子核的自旋逆向旋转,又被原子核排斥。当原子核对电子的吸引力与排斥力在核外某一层次处于平衡态,电子相对稳定下来,并离原子核有一个距离,通常称为电子轨道半径。当两个自旋磁场的自旋逆向旋转时,磁阻会增强。1936年,Mott教授 [8] 提出的二流体模型,将自旋向上和自旋向下的电子分成两个并联的通道,当自旋方向与局域磁矩的方向反向平行的时候,电子受到自旋相关散射增强,电阻大;自旋方向与局域磁矩方向平行排列时,电子受到自旋相关散射减弱,电阻小。这就会导致整个体系处于高低两种阻态。1978年,法国Fert教授 [9] 和德国Grünberg教授 [10] 首次在金属磁性纳米多层膜中发现巨磁电阻效应。基于粒子自旋的原子模型服从以下几个原理:
2.1. 原子核自旋带动电子旋转
原子核自旋磁场与电子自旋磁场有怎样的运动图景?显然不是电子绕原子核运行,而是原子核自旋磁场带动电子自旋磁场一起旋转。因为原子核对电子的吸引力越大,两者之间的磁阻越大,电子在原子核磁场中的自由度越小。原子外“观察者”观察电子,或“探测者”探测电子,好像电子围绕原子核运行,而且有电子轨道。这个电子轨道实际上是原子核自旋带动电子旋转的轨迹。
2.2. 原子核对电子的吸引力达到最大
电子离原子核越近,吸引力越大,电子的能量也越大。在多质子原子中,电子的排布也服从吸引力最大原理。如果原子的电子排布有多层,离核半径小的层必定排满电子,剩余的电子排最后一层。上层电子受到下层电子向上的力,使之不能更接近原子核,离核半径增大。
2.3. 原子核外层电子在同一时间不可能占居同一位置
在原子核磁场中,外层电子磁极同向,自旋方向相同,相互排斥,在同一时间不可能占居同一位置。由于受原子核的吸引,电子之间的距离也有一个吸引力与排斥力相互作用的平衡间距,此时,电子的磁量子态部分叠加。
2.4. 原子核外底层(离核最近层)电子数决定外层电子能级
原子核随着质子数的增加,对电子的吸引力会增强,底层的电子数会增加,各层电子的能量也会增大,即各层电子的能级也会增大。设底层电子数为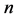 ,
,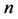 等于1至7中的任一数。
等于1至7中的任一数。
2.5. 底层电子数相同的原子形成一个元素周期
同底层电子数的原子,随着原子核质子数的增加,最外层电子与原子核的距离增加,吸引力减小,能量减小。这样,原子由金属元素,到过渡金属元素,再到非金属元素,最后一个是稀有气体元素,形成一个元素周期。
原子受到电子、光子、热能或磁能的激发,获得能量密度较低的能量,原子体增大,有的甚至被气化。如果底层或中层的电子被激发跃迁,外层电子会适时补位,以保持原子的稳定性。原子在被激发状态下,原子最外层可能有多个电子被激发,这些电子的辐射光谱可能形成光谱的精细结构。光谱的精细结构应是多电子辐射形成,并非单个电子辐射所致。
依据上述原理,可以进行元素周期表中各元素的电子排布。原子核外层电子最大数排布公式:
 (1)
(1)
式中 为元素系数,或元素质子数,
为元素系数,或元素质子数,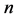 为底层电子数,或外层电子能级,
为底层电子数,或外层电子能级,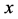 为各元素满足前面各层排满之后的剩余电子数。式中右边各项表示外层电子层次。随着原子系数减小,右式中的中间项从右至左依次去项,见表1。
为各元素满足前面各层排满之后的剩余电子数。式中右边各项表示外层电子层次。随着原子系数减小,右式中的中间项从右至左依次去项,见表1。
3. 基于普朗克常数的原子核外层梯度能级与外层电子能级
原子核自旋梯度磁场,也是一个能量场,从里至外有一个能量梯度,离核越近,能量密度越大,离核越远,能量密度越小。原子核与电子之间的相对运动,即两个自旋磁场的相对运动,产生能量。所谓能量,就是基本粒子磁量子的相对位移量。基本粒子的能量与粒子的质量呈正比,质量越大,能量越大。基本粒子的能量,有两种表述,一般指基本粒子的动能,有时特指用爱因斯坦质能方程式转换的能量。原子核自旋磁场带动电子自旋磁场旋转,两个磁场的相对运动使电子获得更多能量。许多物理学家研究原子核、质子、电子自旋磁矩以及电子轨道磁矩,但对原子内部的电磁现象及原理研究不够。电子在原子核磁场中的运动也服从电磁效应原理。
3.1. 原子核自旋能量场的能级从里至外呈梯度分布
原子核外层的能级可以用电势(电压)来表示,离核半径越小,电势越高,离核半径越大,电势越低。原子受到激发时,外层电子会辐射光子,处于电势高位的电子辐射波长较短的光子,处于电势低位的电子辐射波长较长的光子。元素的辐射光谱精确地反映了原子核外层梯度能级分布。
3.2. 原子核外层电子的能量随着原子核对电子吸引力的增大而增加
外层电子离原子核中心有一个距离为离核半径,也可称为电子轨道半径,半径越小,电子能量越大,半径越大,电子能量越小。电子的能量也可以用电荷来表示。
3.3. 电子的能量与电子的运行速度(磁场相对位移)呈正比
外层电子相对原子外磁场运行速度越大,能量越大。电子自旋磁场的相对位移量可以用电流来表示。电子的运行速度与电子所在原子核外层能级是等效的。原子核带动电子旋转,电子相对于原子核是没有位移的,电子的能量与所处电势的高低相关;原子核带动电子旋转,电子相对于原子的外磁场是有位移的,电子的能量与电子的运行速度相关。外层电子能量随着所处电势的升高而增大,或随着电子运行速度的增加而增大,两者是等效的。
3.4. 电子所在核外层磁量子密度与电阻呈正比
电子所在核外层磁量子密度越大,电子自旋或位移的磁阻(或电阻)越大,反之磁量子密度越小,磁阻越小。
3.5. 原子核外层电子受激发而产生能级变化
原子核外层电子,与原子系数相同数量的电子,受原子核的吸引,处于能级较高的层次。电子吸收入射光子,向外层跃迁,能级降低。电子向外层跃迁,也要做功,消耗能量。金属原子外层的自由电子处于能级较低的层次。原子外磁场加强,自由电子的能级(电势)会提升,反之下降。在导体中,这个能级不会超过金属元素价电子的能级。金属导带能级随着外磁场强度的增大而增加。
1900年,马克斯普朗克 [11] 在研究物体热辐射时提出普朗克常数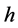 ,该常数值为6.626069574 × 10−34J·s [12] 。普朗克常数
,该常数值为6.626069574 × 10−34J·s [12] 。普朗克常数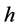 实际上不是光子的能量常数,而是原子核外层电子的能量常数 [13] 。外层电子在一定能级上有一定的波长,如果电子处于辐射光子态,电子的波长与其辐射的光子波长相等。如果将核外电子的能量
实际上不是光子的能量常数,而是原子核外层电子的能量常数 [13] 。外层电子在一定能级上有一定的波长,如果电子处于辐射光子态,电子的波长与其辐射的光子波长相等。如果将核外电子的能量 作为原子核的束缚能,
作为原子核的束缚能,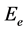 可以表示为
可以表示为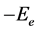 。为了避免歧义,本文用
。为了避免歧义,本文用 表示电子能量。外层电子能量计算公式为:
表示电子能量。外层电子能量计算公式为:
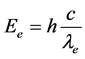 (2)
(2)
式中, 为外层电子能量,单位是
为外层电子能量,单位是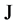 ;
;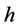 为普朗克常数,单位是
为普朗克常数,单位是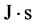 ;
;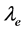 为外层电子的波长,单位是
为外层电子的波长,单位是 ;
;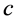 为光速,单位是
为光速,单位是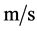 。
。
依据波尔的氢原子理论,氢原子基态电子的速度为光速乘以精细结构常数,外层电子的能量也可用电子相对于原子外磁场的运行速度来进行计算。其公式为:
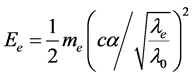 (3)
(3)
式中,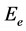 为外层电子的能量,
为外层电子的能量,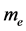 为电子的质量,单位是
为电子的质量,单位是 ;
; 为精细结构常数,
为精细结构常数,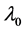 为氢原子基态电子的波长,
为氢原子基态电子的波长,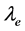 为外层电子的波长。用式(2)与式(3)结合,可以计算普朗克常数:
为外层电子的波长。用式(2)与式(3)结合,可以计算普朗克常数:
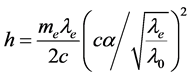 (4)
(4)
依据洛伦兹变换原理,外层电子能量也可以用下面公式计算:
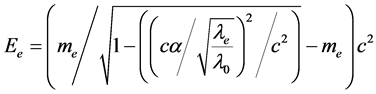 (5)
(5)
用式(2)与式(5)结合,可以计算普朗克常数:
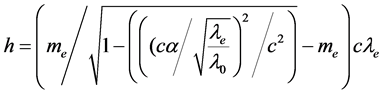 (6)
(6)
依据基本电荷,可用下式计算原子核外层能量场的梯度能级,或电势,或电压:
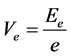 (7)
(7)
式中,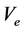 为原子核外层电压,单位是
为原子核外层电压,单位是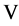 ;
;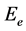 为外层电子的能量,
为外层电子的能量,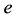 为基本电荷。电子在1伏电压下的电荷值
为基本电荷。电子在1伏电压下的电荷值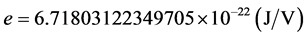 [13] 。1913年,密立根 [14] 通过油滴实验,计算出电子的基本电荷
[13] 。1913年,密立根 [14] 通过油滴实验,计算出电子的基本电荷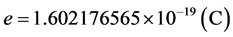 ,这一电荷值实际上不是1伏电势下的电子电荷值,而是238.489002461943伏电势下的电子电荷值。密立根油滴实验原理是科学的,但有些数据处理值得讨论,如在电场中的油滴密度会减小,空气粘滞系数会减小。实验给油滴加载的电势(理论值)为238.489002461943伏,此时油滴上电子的能量应为基本电荷与电势的乘积,电子在1伏电压下的电荷值
,这一电荷值实际上不是1伏电势下的电子电荷值,而是238.489002461943伏电势下的电子电荷值。密立根油滴实验原理是科学的,但有些数据处理值得讨论,如在电场中的油滴密度会减小,空气粘滞系数会减小。实验给油滴加载的电势(理论值)为238.489002461943伏,此时油滴上电子的能量应为基本电荷与电势的乘积,电子在1伏电压下的电荷值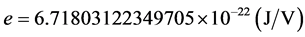 。由式(7)分别与式(2)、式(3)、式(5)结合,可以计算基本电荷:
。由式(7)分别与式(2)、式(3)、式(5)结合,可以计算基本电荷:
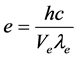 (8)
(8)
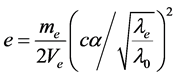 (9)
(9)
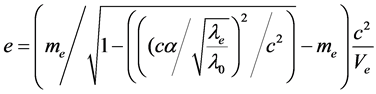 (10)
(10)
这一新的基本电荷值用最小电流法实验可以测量获得。最小电流法实验的基本原理:在一定电势下,电子的能量值是确定的,假设在导体中每一个时点通过一个电子,电子不间断地通过,保持电流不间断,这一电流就是最小电流。1伏电势下最小电流的理论值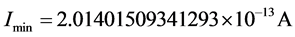 。最小电流的大小与电子能量的大小呈正比。最小电流法的测试电阻为巨电阻
。最小电流的大小与电子能量的大小呈正比。最小电流法的测试电阻为巨电阻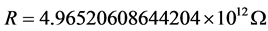 ,每秒通过的电子数
,每秒通过的电子数 。最小电流计算公式:
。最小电流计算公式:
 (11)
(11)
式中,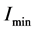 为最小电流,
为最小电流,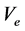 为原子核外层电压,
为原子核外层电压,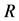 为巨电阻。用下式也可计算最小电流:
为巨电阻。用下式也可计算最小电流:
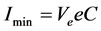 (12)
(12)
式中,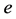 为基本电荷,
为基本电荷,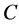 为每秒通过电子数。
为每秒通过电子数。
1916年,密立根光电效应实验 [15] ,也间接地测试了最小电流。下面以光电效应实验数据 、
、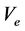 [13] ,用式(2)、式(3)、式(11)计算外层电子能量、电子波长、最小电流。计算结果见表2。
[13] ,用式(2)、式(3)、式(11)计算外层电子能量、电子波长、最小电流。计算结果见表2。
依据原子核外层梯度能级和电子能级公式,可以计算各种金属导电最大电压值。钢的价电子半径约为125 pm,相应电子波长为1.25 × 10−10,用式(2)计算,钢的价电子能量为1.58915796883086 × 10−15。用式(7)计算,钢的价电子所处电压为2365511.43625621电子伏特,用式(11)计算,钢的价电子最小电流为4.76417573626004 × 10−7安培。高压线一般用钢材料制成,特高压不可能达到这个电子伏特。如果接近这个电子伏特,高压线就会损毁。
4. 基于光子静止质量常数的外层电子的光子吸收与辐射
2016年,《普朗克常数与光子静止质量常数统一实验分析》一文 [13] 提出了光子静止质量常数假设,文中公式(2)可用下面公式替代,文中相关公式也应作相应修正。如果将基本粒子看作是一个球体粒子,
Table 1. Element cycle and outer electron distribution table
表1. 元素周期与外层电子排布表
Table 2. Incident photon wavelength, cutoff voltage, electron wavelength, electron energy, minimum current data table of photoelectric effect
表2. 光电效应入射光子波长、截止电压、电子波长、电子能量、最小电流数据表
这个粒子的静止质量与其体积呈反比,体积越大,质量越小,体积越小,质量越大。因此,可以建立光子(基本粒子)静止质量公式:
 (13)
(13)
式中,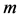 为基本粒子的静止质量,
为基本粒子的静止质量,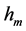 为光子静止质量常数,单位是
为光子静止质量常数,单位是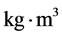 ,
,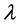 是光子(或基本粒子)的波长。电子质量、电子波长这两个常数通过实验反复证明是非常精确的,因此,可以用来计算光子静止质量常数。2012年国际粒子数据组 [12] 推荐,电子质量
是光子(或基本粒子)的波长。电子质量、电子波长这两个常数通过实验反复证明是非常精确的,因此,可以用来计算光子静止质量常数。2012年国际粒子数据组 [12] 推荐,电子质量 ,电子康普顿波长
,电子康普顿波长 ,则:
,则:
 (14)
(14)
原子在光子、电子、磁场、热能的激发下,可辐射或散射光子。这里,主要论述原子核外层电子如何吸收光子、辐射光子和散射光子。原子核、电子、光子的自旋磁场,从里至外磁量子密度呈梯度分布。入射光子的自旋磁场进入原子核自旋磁场,或进入电子自旋磁场,会与电子的自旋磁场发生碰撞,有弹性碰撞吸收与辐射,有弹性碰撞散射。碰撞的形式由入射光子的波长和外层电子波长或能量决定。入射光子的自旋磁场进入原子核自旋磁场,或进入电子自旋磁场,速度会减慢,光子速度与路径能量密度等效。1992年,Harris等人 [15] 预言原子数密度为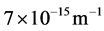 、长度为10 cm的Pb原子气体,可以让波长为283 nm的共振探测光的群速度减慢到
、长度为10 cm的Pb原子气体,可以让波长为283 nm的共振探测光的群速度减慢到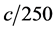 。1999年,美国哈佛大学的Hau研究小组 [16] 利用Na原子的玻色–爱因斯坦凝聚体成功地将光速降到
。1999年,美国哈佛大学的Hau研究小组 [16] 利用Na原子的玻色–爱因斯坦凝聚体成功地将光速降到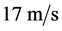 。近年来,L.V.Hau 等人 [17] [18] [19] 用电磁诱导透明(EIT)方法减慢光速,揭示了电磁与光的一些相互作用原理。
。近年来,L.V.Hau 等人 [17] [18] [19] 用电磁诱导透明(EIT)方法减慢光速,揭示了电磁与光的一些相互作用原理。
4.1. 原子核外层电子与入射光子的弹性碰撞吸收与辐射
所谓弹性碰撞吸收与辐射,是指入射光子能量等于电子能量时,入射光子自旋磁场与电子自旋磁场发生碰撞,光子被电子完全吸收。由于光子的能量密度小于电子的能量密度,吸收光子的电子会向外层跃迁,到达激发态顶点辐射一个光子;电子受原子核的吸引立即回迁,到下一个点再辐射一个光子,直到回迁至基态。入射光子波长大于外层电子波长,并且两者能量相等,才能产生弹性碰撞吸收。吸收光子的电子,能量密度减小,向外层跃迁;电子到达激发态顶点,辐射一个光子,能量密度增加,向内层回迁。外层电子吸收一个光子,可以辐射多个光子。辐射光子的波长与电子在辐射层次的波长相等。入射光子的波长越短,入射至原子核自旋磁场和电子的自旋磁场的层次越深,反之,越浅。
原子核外层电子能量与入射光子的能量相等。入射光子能量用下式计算:
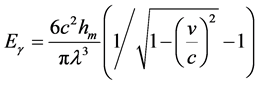 (15)
(15)
式中,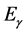 为入射光子能量,
为入射光子能量,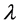 为入射光子波长,
为入射光子波长,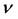 为光子的速度,
为光子的速度, 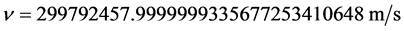 [13] 。
[13] 。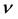 接近光速
接近光速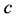 ,光子的动能接近光子的能量,式中“−1”可以省略。辐射光子的能量也可用式(15)计算,
,光子的动能接近光子的能量,式中“−1”可以省略。辐射光子的能量也可用式(15)计算, 则为辐射光子波长。与外层电子(自由电子)发生弹性碰撞吸收的光子的波长远远大于该外层电子(自由电子)辐射光子的波长。吸收光子波长与辐射光子波长用下式计算:
则为辐射光子波长。与外层电子(自由电子)发生弹性碰撞吸收的光子的波长远远大于该外层电子(自由电子)辐射光子的波长。吸收光子波长与辐射光子波长用下式计算:
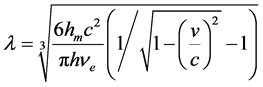 (16)
(16)
式中,计算入射光子波长时,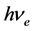 为发生弹性碰撞吸收的电子(或基态)能量;计算辐射光子波长时,
为发生弹性碰撞吸收的电子(或基态)能量;计算辐射光子波长时,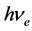 为辐射光子的电子(或激发态)能量。
为辐射光子的电子(或激发态)能量。
4.2. 原子核外层电子与入射光子的弹性散射
所谓弹性散射,是指入射光子自旋磁场进入原子核自旋磁场和外层电子自旋磁场时,入射光子波长约等于外层电子波长,两者发生弹性碰撞散射。散射光子有一定的波长范围,入射光子波长与外层电子波长相等,发生正向弹性碰撞散射,产生散射光子波长的峰值;入射光子的波长略小于或大于外层电子波长,发生偏正弹性碰撞散射,产生散射光子波长峰值两侧的值。弹性散射的外层电子能量用下式计算:
 (17)
(17)
式中,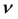 为散射光子的频率或散射光子的外层电子的频率。依据式(16)可以计算散射光子的波长。式中,
为散射光子的频率或散射光子的外层电子的频率。依据式(16)可以计算散射光子的波长。式中,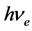 为散射光子的外层电子能量。
为散射光子的外层电子能量。
5. 氢原子光谱与精细结构常数分析
1853年安德斯∙约纳斯∙埃格斯特朗(Anders Jonas Ångström)从气体放电的光谱中找到氢的红线光谱 ,并测定其波长为656.21 nm,以后在可见光区又陆续发现了深绿
,并测定其波长为656.21 nm,以后在可见光区又陆续发现了深绿 、青
、青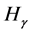 、紫
、紫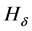 几条光谱线,波长分别为486.074 nm、434.01 nm、410.12 nm。1885年巴尔末(J.Balmer)仔细分析这些光谱线的波长,建立巴尔末公式,并计算出与实验吻合很好的巴尔末线系。1890年,里德伯建立氢原子光谱公式和里德伯常数。1906年莱曼(T.Luman)在氢光谱紫外区发现一线系,1908年、1922年和1924年,帕邢(F.Paschen)、布喇开(F.Bradkett)和普丰特(H.Pfund)分别在氢光谱红外区各发现一个线系,以及上世纪50年代初发现汉弗莱斯(Humphreys)线系。氢原子光谱公式:
几条光谱线,波长分别为486.074 nm、434.01 nm、410.12 nm。1885年巴尔末(J.Balmer)仔细分析这些光谱线的波长,建立巴尔末公式,并计算出与实验吻合很好的巴尔末线系。1890年,里德伯建立氢原子光谱公式和里德伯常数。1906年莱曼(T.Luman)在氢光谱紫外区发现一线系,1908年、1922年和1924年,帕邢(F.Paschen)、布喇开(F.Bradkett)和普丰特(H.Pfund)分别在氢光谱红外区各发现一个线系,以及上世纪50年代初发现汉弗莱斯(Humphreys)线系。氢原子光谱公式:
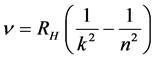 (18)
(18)
式中,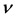 为光子频率,
为光子频率, 为里德伯常数,
为里德伯常数,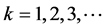 ,
,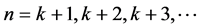 。
。
依据本文相关公式,可以计算氢原子光谱的光子波长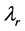 、外层电子波长
、外层电子波长 、入射光子的波长
、入射光子的波长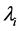 、辐射光子能量
、辐射光子能量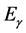 、外层电子能量
、外层电子能量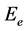 、里德伯常数公式计算的光子波长
、里德伯常数公式计算的光子波长 ,用表三描述。
,用表三描述。
依据表三的数据,氢原子光谱和精细结构常数可作如下解释。
5.1. 基态电子吸收能量相等的入射光子产生受激辐射
基态电子的能量与入射光子的能量相等,每个线系都有一个基态电子。基态电子的能量用式(2)、式(3)、和式(5)均可计算,入射光子的能量用式(15)计算。氢原子在特定的电场、磁场、热能条件下,电子处于特定的线系运动范围,可以用莱曼等线系描述。处于光谱线系的基态电子吸收能量相等的入射光子,向外层跃迁,到达激发态顶点,辐射一个光子,再回迁,随之辐射一系列的光子,直至回到基态。如果将每一个线系的第一个光子对应的外层电子(表3中加粗线描述的光子波长或电子波长)作为基态电子,另外5个为辐射光子,该基态电子受激发后相继辐射一系列光子。
5.2. 外层电子辐射光子时的波长与其辐射的光子波长相等
处于特定能级的外层电子具有特定的波长,简称外层电子波长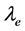 (或轨道电子波长)。外层电子的波长与其辐射的光子波长
(或轨道电子波长)。外层电子的波长与其辐射的光子波长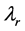 相等。外层电子的波长用式(2)推导计算,辐射光子波长用式(16)计算。
相等。外层电子的波长用式(2)推导计算,辐射光子波长用式(16)计算。
5.3. 辐射光子的能量之和等于入射光子的能量
处于基态的电子吸收一个入射光子,辐射一系列的光子,辐射光子的能量用式(15)计算。辐射光子的能量之和等于入射光子的能量。每个线系辐射光子数是有限的,不是无穷的。
5.4. 里德伯常数是波尔基态电子波长的倒数
依据波尔基态电子能量,用式(2)计算得波尔基态电子波长为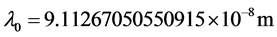 。这一波长的倒数是里德伯常数,
。这一波长的倒数是里德伯常数, [12] 。在式(3)、式(5)中,
[12] 。在式(3)、式(5)中,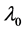 为氢原子基态电子波长。由式(2)与式(3)结合,计算里德伯常数:
为氢原子基态电子波长。由式(2)与式(3)结合,计算里德伯常数:
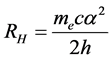 (19)
(19)
由式(19)也可以求普朗克常数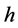 。由式(3)与式(7)结合,也可计算里德伯常数:
。由式(3)与式(7)结合,也可计算里德伯常数:
Table 3. Hydrogen atomic spectrum related data table
表3. 氢原子光谱相关数据表
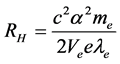 (20)
(20)
式中,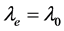 。
。
5.5. 氢原子光谱与精细结构常数的联系
精细结构常数与很多物理常数有着十分密切的联系。这里主要讨论精细结构常数与氢原子光谱相关的几个问题。波尔提出光速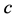 乘以精细结构常数
乘以精细结构常数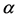 为基态电子的轨道速度。由式(2)与式(3)结合,计算精细结构常数:
为基态电子的轨道速度。由式(2)与式(3)结合,计算精细结构常数:
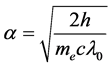 (21)
(21)
由式(3)与式(7)结合,也可计算精细结构常数:
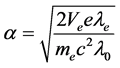 (22)
(22)
从表三可以看出,莱曼线基态电子波长,除以汉弗莱线系第一个辐射光子的波长,获得精细结构常数。汉弗莱线系第一个辐射光子的波长为氢原子精细结构常数波长,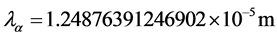 。用里德伯氢原子光谱公式计算,这一波长的值等于
。用里德伯氢原子光谱公式计算,这一波长的值等于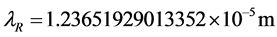 ,略小于氢原子精细结构常数波长。
,略小于氢原子精细结构常数波长。
表三中的实验数据 为巴尔末系实验数据(见图1) [20] ,略大于里德伯氢原子光谱公式计算的波长。从大量氢原子光谱实验数据分析,辐射光子的波长略大于里德伯氢原子光谱公式计算的波长,趋向氢原子精细结构常数波长分布。
为巴尔末系实验数据(见图1) [20] ,略大于里德伯氢原子光谱公式计算的波长。从大量氢原子光谱实验数据分析,辐射光子的波长略大于里德伯氢原子光谱公式计算的波长,趋向氢原子精细结构常数波长分布。
6. 结论
本文基于粒子自旋实验分析,提出了基于粒子自旋的原子模型,论述了原子核与电子的相互作用、

Figure 1. Emission dpectrum of the hydrogen atom in the visible and near violet region [Balmer series, Herzberg (41)]. 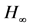 gives the theoretical on of the series limit
gives the theoretical on of the series limit
图1. 氢原子可见光和附近紫色光发射光谱[巴尔末线系,Herzberg (41)]。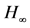 为该线系理论极限
为该线系理论极限
原子运动的机理和原子模型,论述了原子外层电子排布与元素周期的一致性。基于对普朗克常数和相关实验分析,进一步论证了普朗克常数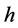 不是光子的能量常数,而是原子核外层电子的能量常数,阐述了原子核外层梯度能级、外层电子能量,以及基本电荷、电压、最小电流等电磁效应原理。基于光子(基本粒子)静止质量常数假设,论述了电子与光子的相互作用及光电效应原理。最后,运用上述原理对氢原子实验数据进行分析,论述了氢原子光谱与精细结构常数的联系。文章还提到原子核结构和磁量子等问题,由于篇幅有限,没有作深入探讨。本文对原子模型一些基本问题的讨论,将对原子物理学的发展开拓新的思路,对原子物理学的应用展示广阔的前景。
不是光子的能量常数,而是原子核外层电子的能量常数,阐述了原子核外层梯度能级、外层电子能量,以及基本电荷、电压、最小电流等电磁效应原理。基于光子(基本粒子)静止质量常数假设,论述了电子与光子的相互作用及光电效应原理。最后,运用上述原理对氢原子实验数据进行分析,论述了氢原子光谱与精细结构常数的联系。文章还提到原子核结构和磁量子等问题,由于篇幅有限,没有作深入探讨。本文对原子模型一些基本问题的讨论,将对原子物理学的发展开拓新的思路,对原子物理学的应用展示广阔的前景。
文章引用
吴先金. 基于粒子自旋的原子模型与实验分析
Atomic Model and Experimental Analysis Based on Particle Spin[J]. 现代物理, 2017, 07(04): 94-105. http://dx.doi.org/10.12677/MP.2017.74011
参考文献 (References)
- 1. Kwiat, P.G., Mattle, K., Weinfurter, H., Zeilinger, A., Sergienko, A.V. and Shih, Y.H. (1995) New High Intensity Source of Polarization Entangled Photon Pairs. Physical Review Letters, 75, 4337-4341. https://doi.org/10.1103/PhysRevLett.75.4337
- 2. Hall, E.H. (1897) On a New Action of the Magnet on Electric Currents. American Journal of Mathematics, 2, 3.
- 3. Hall, E.H. (1880) On the New Action of Magnetism on a Permanent Electric Current. Philosophical Magazine, 10, 301. https://doi.org/10.1080/14786448008626936
- 4. Klitzing, K.V., Dorda, G. and Pepper, M. (1980) New Method for High-Accuracy Determination of the Fin×10-Struc- ture Constant Based Quantized Hall Resistance. Physical Review Letters, 45, 494. https://doi.org/10.1103/PhysRevLett.45.494
- 5. Murakami, S., Nagaosa, N. and Zhang, S.C. (2003) Dissipa-tionless Quantum Spin Current at Room Temperature. Science, 301, 1348-1351. https://doi.org/10.1126/science.1087128
- 6. Sinova, J., Culcer, D., Niu, Q., et al. (2004) Universal Intrinsic Spin Hall Effect. Physical Review Letters, 92, 126603. https://doi.org/10.1103/PhysRevLett.92.126603
- 7. Chang, C.Z., Zhang, J.S. and Feng, X. (2013) Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science, 340, 167. https://doi.org/10.1126/science.1234414
- 8. Mott, N.F. and Jones, H. (1936) The Theory of the Properties of Metals and Alloys. Oxford University Press, Oxford.
- 9. Baibieh, M.N., Broto, J.M., Fert, A., Nguyen Van Dau, F., Petroff, F., Eitenne, P., Creuzet, G., Friederich, A. and Chazelas, J. (1988) Giant Magneto Resistance of (001)Fe/(001)Cr Magnetic Super Lattices. Physical Review Letters, 61, 2472.
- 10. Binasch, G., Grünberg, P., Saurenbach, F. and Zinn, W. (1989) Enhanced Magnetoresistance in Layered Magnetic Structures with Antiferromagnetic Interflayer Exchange. Physical Review B, 39, 4828. https://doi.org/10.1103/PhysRevB.39.4828
- 11. Planck, M. (1901) On the Law of Distribution of Energy in the Normal Spectrum. Annalen der Physik, 4, 553. https://doi.org/10.1002/andp.19013090310
- 12. Mohr, P.J., Taylor, B.N. and Newell, D.B. (2012) CODATA Recommended Values of the Fundamental Physical Constants: 2010. Reviews of Modern Physics, 84, 1586.
- 13. 吴先金. 普朗克常数与光子静止质量常数统一实验分析[J]. 现代物理, 2016, 6(6): 183-193. https://image.hanspub.org/pdf/MP20160600000_45285564.pdf
- 14. Millikan, R.A. (1913) On the Elementary Electrical Charge and the Avogadro Constant. Physical Review, 2, 109-143. http://authors.library.caltech.edu/6438/1/MILpr13b.pdf https://doi.org/10.1103/PhysRev.2.109
- 15. Millikan, R.A. (1916) A Direct Photoelectric Determination of Planck’s “H”. Physical Review, 7, 355-388. https://doi.org/10.1103/PhysRev.7.355
- 16. Haurs,S.E., Field, J.E. and Kasapi, A. (1992) Dispersive Properties of Electromagnetically Induced Transparency. Physical Review, 46, 29. https://doi.org/10.1103/PhysRevA.46.R29
- 17. Hau, L.V., Haurs, S.E., Dutton, Z. and ßehroozi, C.H. (1999) Light Speed Reduction to 17 Metres per Second in an Ultracold Atomic Gas. Nature, 397, 594. https://doi.org/10.1038/17561
- 18. Haurs, S.E. and Hau, L.V. (1999) Nonlinear Optics at Low Light Levels. Physical Review Letters, 82, 4611. https://doi.org/10.1103/PhysRevLett.82.4611
- 19. Fleisehhauer, M. and Lukin, M.D. (2000) Dark-State Polaritons in Electromagnetically Induced Transparency. Physical Review Letters, 84, 5094. https://doi.org/10.1103/PhysRevLett.84.5094
- 20. Herzberg, G. (2007) Atomic Spectra and Atomic Structure. Prentice-Hall, Upper Saddle River, New Jersey.
