Applied Physics
Vol.06 No.08(2016), Article ID:18426,9
pages
10.12677/APP.2016.68023
Dynamics Evolution Characteristic of Incoherent Bright Spatial Solitons in LiNbO3 Crystal
Guangwen Huo1*, Heng Chen1, Meizhi Zhang2
1College of Control Engineering, Xijing University, Xi’an Shaanxi
2School of Electronics Engineering, Xi’an University of Posts and Telecommunications, Xi’an Shaanxi
Email: *guangwenhuo@126.com
Received: Aug. 10th, 2016; accepted: Aug. 25th, 2016; published: Aug. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We theoretically study the formation mechanism and dynamic evolution characteristics of incoherent bright photovoltaic (PV) solitons in self-defocusing LiNbO3 crystal. It is found that the transition of self-defocusing to self-focusing can be realized by adding a background beam in LiNbO3 crystal, and bright spatial solitons generate under suitable conditions. Taking LiNbO3 as an example, we give the relationship between the spatial distribution of refractive index and the ratio of PV constant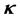 . We then calculate the existence curve of bright PV solitons. Furthermore, we analyze the propagation characteristics of incoherent bright PV solitons using coherent density approach, and simulate how the soliton formation is influenced by
. We then calculate the existence curve of bright PV solitons. Furthermore, we analyze the propagation characteristics of incoherent bright PV solitons using coherent density approach, and simulate how the soliton formation is influenced by  values with split-step Fourier method. The bright incoherent PV solitons are affected by intensity ratios
values with split-step Fourier method. The bright incoherent PV solitons are affected by intensity ratios 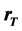 and the width of source angular power spectrum
and the width of source angular power spectrum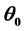 . It realizes the switching of bright and dark solitons by adding a background beam without extra bias voltage, which provides useful reference for all optical devices design based on solitons.
. It realizes the switching of bright and dark solitons by adding a background beam without extra bias voltage, which provides useful reference for all optical devices design based on solitons.
Keywords:Spatial Solitons, Transition of Self-Defocusing to Self-Focusing, Spatial Evolution, Coherent Density Approach

LiNbO3晶体中非相干空间亮孤子的 动态演化特性
霍广文1*,陈恒1,张美志2
1西京学院控制工程学院,陕西 西安
2西安邮电大学电子工程学院,陕西 西安

收稿日期:2016年8月10日;录用日期:2016年8月25日;发布日期:2016年8月30日

摘 要
本文理论研究了自散焦LiNbO3晶体中非相干亮光伏孤子的形成机理及其动态演化特性。研究发现,通过加载背景光的方法能够实现LiNbO3晶体由自散焦向自聚焦的转换并形成亮空间孤子。以LiNbO3晶体为例,给出了折射率空间分布与光伏常数比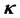 之间的关系,给出了亮光伏孤子的存在曲线。进一步采用相干密度法理论分析了非相干亮光伏孤子在LiNbO3晶体中的传输特性,并利用分步傅里叶算法数值模拟了
之间的关系,给出了亮光伏孤子的存在曲线。进一步采用相干密度法理论分析了非相干亮光伏孤子在LiNbO3晶体中的传输特性,并利用分步傅里叶算法数值模拟了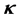 值对孤子形成的影响。此外,非相干亮光伏孤子的形成还受强度比值
值对孤子形成的影响。此外,非相干亮光伏孤子的形成还受强度比值 和光源角功率谱宽度
和光源角功率谱宽度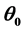 的影响。通过加载背景光的方法可以实现无偏压条件下亮暗孤子的切换,这对基于孤子的全光器件研究提供可靠性参考。
的影响。通过加载背景光的方法可以实现无偏压条件下亮暗孤子的切换,这对基于孤子的全光器件研究提供可靠性参考。
关键词 :空间孤子,自散焦向自聚焦转换,空间演化,相干密度法

1. 引言
光折变空间孤子在光开关、光互联等非线性光器件方面具有巨大的潜在应用价值,近二十年来受到人们的广泛关注。通常情况下,光折变空间孤子分为准稳态孤子 [1] ,屏蔽孤子 [2] 和光伏孤子 [3] 三种类型,而后两者尤其引人注目。屏蔽孤子和光伏孤子形成的物理机制不同。屏蔽孤子在外加偏压作用下通过非线性效应改变材料折射率,从而形成空间孤子;光伏孤子的形成不需要外加电场,光照区激发载流子,在光伏效应下形成孤子,具有很强的光伏电流。铁电晶体中,空间电场的形成是载流子沿轴向迁移累积的结果。在开路条件下( ),光伏晶体的折射率变化为
),光伏晶体的折射率变化为 ,其中
,其中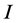 ,
, ,
,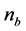 ,
, 和
和 分别为光束强度,暗辐射,无微扰折射率,有效电光系数和最大光伏场。在自聚焦光伏材料中,折射率变化是正值,可以形成亮光伏孤子 [4] ;在自散焦材料中,折射率变化为负值,能够产生暗光伏孤子 [5] 。该类型亮、暗光伏孤子在理论和实验上已经得到证明,其诱导的波导和方向耦合器也被实验研究 [6] - [8] 。与传统光伏空间孤子不同,通过加载背景光的方法可以实现光伏晶体自散焦与自聚焦的相互转换,这一现象由Anastassiou等人于1998年首次报道 [9] 。随后,刘思敏课题组研究了背景光照对材料自散焦和自聚焦转换的影响 [10] [11] 。2006年,佘卫龙等人在LiNbO3晶体中实验观察到二维亮光伏孤子 [12] 。随后几年,卢克清课题组在LiNbO3晶体中实验观察到一维亮光伏孤子,并分析了该孤子的调制不稳定性 [13] [14] 。然而,关于LiNbO3晶体中亮光伏孤子空间传输的动态演化特性却研究很少。非相干空间孤子的发现为孤子科学和非线性光学科学开辟了新的研究领域,在过去的十几年间一直是国际科研工作者研究的热点问题。目前,关于非相干孤子在理论上和实验上虽然都有较为完备的论述 [15] [16] ,但在自散焦光折变晶体中形成的非相干亮光伏孤子,其非线性传输特性还未曾报道。研究该新型亮光伏孤子的动态演化特性对基于孤子全光器件的设计具有重要意义。
分别为光束强度,暗辐射,无微扰折射率,有效电光系数和最大光伏场。在自聚焦光伏材料中,折射率变化是正值,可以形成亮光伏孤子 [4] ;在自散焦材料中,折射率变化为负值,能够产生暗光伏孤子 [5] 。该类型亮、暗光伏孤子在理论和实验上已经得到证明,其诱导的波导和方向耦合器也被实验研究 [6] - [8] 。与传统光伏空间孤子不同,通过加载背景光的方法可以实现光伏晶体自散焦与自聚焦的相互转换,这一现象由Anastassiou等人于1998年首次报道 [9] 。随后,刘思敏课题组研究了背景光照对材料自散焦和自聚焦转换的影响 [10] [11] 。2006年,佘卫龙等人在LiNbO3晶体中实验观察到二维亮光伏孤子 [12] 。随后几年,卢克清课题组在LiNbO3晶体中实验观察到一维亮光伏孤子,并分析了该孤子的调制不稳定性 [13] [14] 。然而,关于LiNbO3晶体中亮光伏孤子空间传输的动态演化特性却研究很少。非相干空间孤子的发现为孤子科学和非线性光学科学开辟了新的研究领域,在过去的十几年间一直是国际科研工作者研究的热点问题。目前,关于非相干孤子在理论上和实验上虽然都有较为完备的论述 [15] [16] ,但在自散焦光折变晶体中形成的非相干亮光伏孤子,其非线性传输特性还未曾报道。研究该新型亮光伏孤子的动态演化特性对基于孤子全光器件的设计具有重要意义。
本文以Vinetskii-Kukhtarev带输运模型为基础,理论研究了自散焦介质中亮光伏孤子的形成机理及其动态演化特性,分析背景光对晶体折射率变化和孤子传输特性的影响。选用LiNbO3晶体为例,首先计算了折射率空间分布随背景光与孤子光的光伏常数比值 之间的关系,给出了亮光伏孤子的存在曲线。然后,进一步采用相干密度法理论描述了非相干光伏孤子的传输特性,并利用分步傅里叶算法数值模拟了非相干高斯光束在不同
之间的关系,给出了亮光伏孤子的存在曲线。然后,进一步采用相干密度法理论描述了非相干光伏孤子的传输特性,并利用分步傅里叶算法数值模拟了非相干高斯光束在不同 值下的传输特性,分析背景光对非相干孤子空间演化特性的影响。此外,理论研究了强度比值
值下的传输特性,分析背景光对非相干孤子空间演化特性的影响。此外,理论研究了强度比值 和光源角功率谱宽度
和光源角功率谱宽度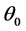 对非相干亮光伏孤子形成的影响。
对非相干亮光伏孤子形成的影响。
2. 自散焦介质中的带输运模型
在光折变晶体中,光折变效应由标准速率方程,连续性方程和高斯定律描述,其理论基础为单电子载流子模型。假设光强为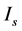 的孤子光束沿
的孤子光束沿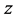 轴传播,只在
轴传播,只在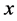 方向发生衍射,其偏振方向与晶轴平行,并且晶轴与
方向发生衍射,其偏振方向与晶轴平行,并且晶轴与 轴平行。另外,假设有一束均匀背景光照射晶体,强度为
轴平行。另外,假设有一束均匀背景光照射晶体,强度为 ,其偏振方向与晶轴垂直。在一维稳态条件下,上述方程可表述为 [9] [12] [13]
,其偏振方向与晶轴垂直。在一维稳态条件下,上述方程可表述为 [9] [12] [13]
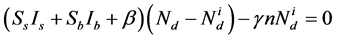 ( 1a )
( 1a )
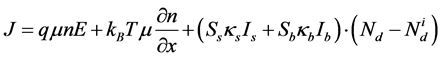 (1b)
(1b)
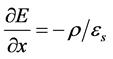 ( 1c )
( 1c )
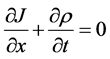 (1d)
(1d)
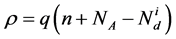 (1e)
(1e)
上式中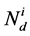 为电离施主浓度,
为电离施主浓度,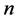 为自由电子密度,
为自由电子密度,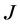 为电流密度,
为电流密度,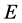 为晶体内的空间电场,
为晶体内的空间电场,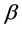 为晶体的暗辐射率。相关的晶体参数为总的施主密度
为晶体的暗辐射率。相关的晶体参数为总的施主密度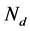 ,负电子受主密度
,负电子受主密度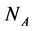 ,复合系数
,复合系数 ,低频介电常数
,低频介电常数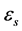 ,电子速率
,电子速率 ,波尔兹曼常数
,波尔兹曼常数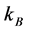 和绝对温度
和绝对温度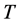 。
。 ,
,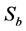 分别为孤子光束和背景光束的光致电离交叉系数。
分别为孤子光束和背景光束的光致电离交叉系数。 是背景光和孤子光的光伏常数之比,与材料和入射波长有关。在方程(
是背景光和孤子光的光伏常数之比,与材料和入射波长有关。在方程(
律我们得到 ,其中
,其中 是晶体电极之间的电压,
是晶体电极之间的电压,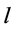 是两个电极之间的宽度,
是两个电极之间的宽度,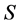 是电极的表面面积,
是电极的表面面积,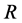 是外加电阻。
是外加电阻。
在方程(
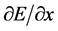 和电子密度
和电子密度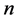 ,由于
,由于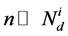 ,
, ,可以得到空间电场 [9]
,可以得到空间电场 [9]
 (2)
(2)
在开路条件下(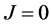 ),忽略晶体的暗辐射,方程(2)可化为
),忽略晶体的暗辐射,方程(2)可化为
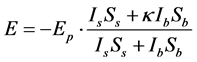 (3)
(3)
其中 。将方程(3)代入折射率变化公式
。将方程(3)代入折射率变化公式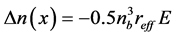 ,得
,得
 (4)
(4)
其中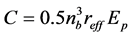 ,
,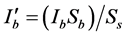 。
。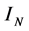 为归一化光强。
为归一化光强。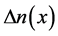 的符号由参数
的符号由参数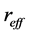 和
和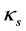 共同决定。在LiNbO3晶体中,
共同决定。在LiNbO3晶体中,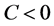 ,背景光强度是均匀的,
,背景光强度是均匀的,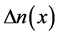 的空间分布由
的空间分布由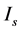 决定。图1是
决定。图1是 分别取0,0.5,1,1.5,2时,LiNbO3晶体折射率变化随孤子光强度变化的曲线。图中显示,当
分别取0,0.5,1,1.5,2时,LiNbO3晶体折射率变化随孤子光强度变化的曲线。图中显示,当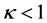 包含
包含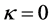 时,折射率的变化随着
时,折射率的变化随着 的增加而减少,晶体表现出自散焦现象,可以形成暗孤子;当
的增加而减少,晶体表现出自散焦现象,可以形成暗孤子;当 时,折射率的变化随着
时,折射率的变化随着 的增加而增加,表现出自聚焦现象,满足亮孤子形成条件;当
的增加而增加,表现出自聚焦现象,满足亮孤子形成条件;当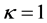 时,
时,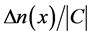 是常数,孤子光束既没有自散焦现象也没有自聚焦现象,犹如透过线性介质,不能形成孤子。因而,在自散焦晶体中
是常数,孤子光束既没有自散焦现象也没有自聚焦现象,犹如透过线性介质,不能形成孤子。因而,在自散焦晶体中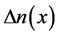 随
随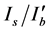 的变化规律取决于光伏常数之比
的变化规律取决于光伏常数之比 ,而
,而 的大小与晶体和入射波长有关。对于LiNbO3晶体来说,短波长的光具有较大的光伏常数,为了得到
的大小与晶体和入射波长有关。对于LiNbO3晶体来说,短波长的光具有较大的光伏常数,为了得到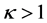 的亮孤子条件,入射的背景光必须比孤子光波长短。但无论
的亮孤子条件,入射的背景光必须比孤子光波长短。但无论 取何值,折射率变化
取何值,折射率变化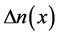 始终为负数,不能改变晶体类型。
始终为负数,不能改变晶体类型。
以高斯分布的信号光为例,其光强可表示为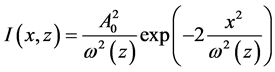 ,如图2(a)所示在。将该
,如图2(a)所示在。将该
高斯光束入射到LiNbO3晶体,并加一束强度均匀的背景光束。晶体折射率变化的空间分布除了与入射光束的强度分布有关,同样与两束光的光伏常数之比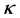 有关。图2(b)和图2(c)分别为高斯信号光照射下
有关。图2(b)和图2(c)分别为高斯信号光照射下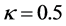 和
和 时晶体折射率的空间分布图。从图2看到,在自散焦LiNbO3晶体中,当
时晶体折射率的空间分布图。从图2看到,在自散焦LiNbO3晶体中,当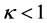 时,折射
时,折射
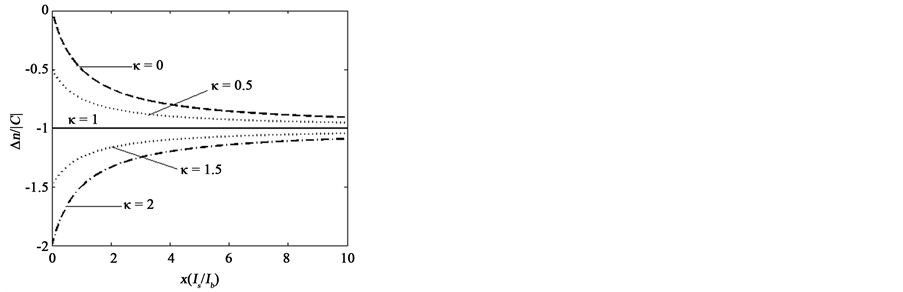
Figure 1. The refractive index change varying with intensity for different 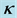 values
values
图1. 折射变化在不同 值下随强度变化
值下随强度变化

Figure 2. (a) The Gaussian profile of incident beam; the spatial distribution of refractive index with (b)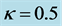 ; (c)
; (c)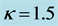
图2. (a) 高斯入射光强度包络;折射率的空间分布; (b)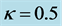 ; (c)
; (c)
率中间小边缘大,类似于凹透镜,具有自散焦效应,如图2(b)所示;当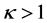 时,晶体折射率中间大边缘小,类似于凸透镜,具有自聚焦效应。虽然
时,晶体折射率中间大边缘小,类似于凸透镜,具有自聚焦效应。虽然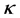 取不同数值会改变折射率的空间分布,表现出自散焦或者自聚焦现象,但折射率变化始终是负值。
取不同数值会改变折射率的空间分布,表现出自散焦或者自聚焦现象,但折射率变化始终是负值。
3. 亮光伏孤子形成
假设信号光场 (
(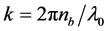 ),
), 是自由空间中的波长,在慢变幅近似和傍轴近似条件下,满足标量波方程
是自由空间中的波长,在慢变幅近似和傍轴近似条件下,满足标量波方程
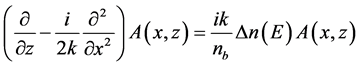 (5)
(5)
这里 由方程(4)表示。假设满足方程(5)的孤子解具有形式
由方程(4)表示。假设满足方程(5)的孤子解具有形式
 (6)
(6)
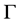 是孤子的传输常数,
是孤子的传输常数, 是归一化振幅。将方程(2)和(6)带入方程(5),可得方程 [8]
是归一化振幅。将方程(2)和(6)带入方程(5),可得方程 [8]
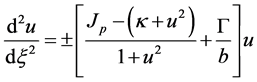 (7)
(7)
方程中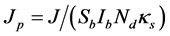 ,无量纲参数
,无量纲参数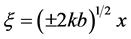 ,而
,而 。方程中的正负号与
。方程中的正负号与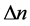 符号一致。
符号一致。
在开路条件下(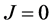 ),选用LiNbO3晶体,方程(7)化为
),选用LiNbO3晶体,方程(7)化为
 (8)
(8)
当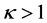 ,且满足边界条件
,且满足边界条件 ,及初始条件
,及初始条件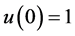 ,
, ,方程(8)可以得到亮孤子。
,方程(8)可以得到亮孤子。
利用LiNbO3晶体的参数,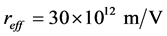 ,
, 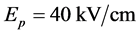 ,
, 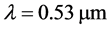 ,
,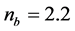 ,数值求解方程(8)可以得到亮光伏孤子解。图3描述了
,数值求解方程(8)可以得到亮光伏孤子解。图3描述了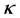 分别为1.1,1.5,2三种情况下亮孤子的归一化强度。从图中看到,随着
分别为1.1,1.5,2三种情况下亮孤子的归一化强度。从图中看到,随着 值的增大,亮光伏孤子的宽度逐渐变窄,晶体内光学非线性效应增加。
值的增大,亮光伏孤子的宽度逐渐变窄,晶体内光学非线性效应增加。
调节信号光和背景光的强度,假设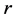 是
是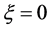 处孤子峰值强度与
处孤子峰值强度与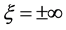 处光强之比,若将
处光强之比,若将 代入方程(8),通过数值求解方法可以得到亮光伏孤子宽度随光强比值
代入方程(8),通过数值求解方法可以得到亮光伏孤子宽度随光强比值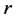 的变化曲线,如图4所示。从图中看到,当光强比值在1附近,孤子具有最小宽度;当光强比值逐渐变大时孤子宽度也增大;而在光强比值小于1时,随着强度比值的减小,孤子宽度急剧增大,形成的孤子具有不稳定性。LiNbO3晶体中所形成的亮光伏孤子与传统光伏孤子具有类似的存在曲线。
的变化曲线,如图4所示。从图中看到,当光强比值在1附近,孤子具有最小宽度;当光强比值逐渐变大时孤子宽度也增大;而在光强比值小于1时,随着强度比值的减小,孤子宽度急剧增大,形成的孤子具有不稳定性。LiNbO3晶体中所形成的亮光伏孤子与传统光伏孤子具有类似的存在曲线。
所以,光伏孤子和屏蔽孤子在折射率变化方面主要有两点不同。首先,屏蔽孤子的折射率变化可以通过改变外加电场得到控制,电场的极性决定着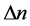 的符号。对于光伏孤子来说,折射率变化
的符号。对于光伏孤子来说,折射率变化 的符号取决于电光系数
的符号取决于电光系数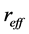 和光伏常数
和光伏常数 。对于给定的波长和偏振,该系数是不变的(比如,LiNbO3的
。对于给定的波长和偏振,该系数是不变的(比如,LiNbO3的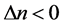 ,BaTiO3的
,BaTiO3的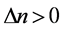 )。另外,对于屏蔽孤子和传统光伏孤子来说,加一束背景光不会增加新的物理现象,只能增加背景光在晶体导带中载流子浓度,相当于增加了晶体的暗辐射系数
)。另外,对于屏蔽孤子和传统光伏孤子来说,加一束背景光不会增加新的物理现象,只能增加背景光在晶体导带中载流子浓度,相当于增加了晶体的暗辐射系数 。而对于LiNbO3晶体中的亮光伏孤子来说,背景光束增加了一项额外的光伏电流,实现了自散焦向自聚焦转换的新物理现象。
。而对于LiNbO3晶体中的亮光伏孤子来说,背景光束增加了一项额外的光伏电流,实现了自散焦向自聚焦转换的新物理现象。
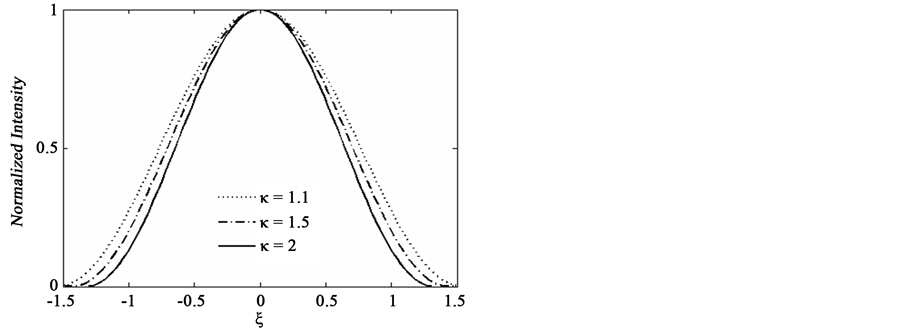
Figure 3. The normalized intensity profiles of bright PV soliton with different  values
values
图3. 亮光伏孤子在不同 值下的归一化强度包络
值下的归一化强度包络
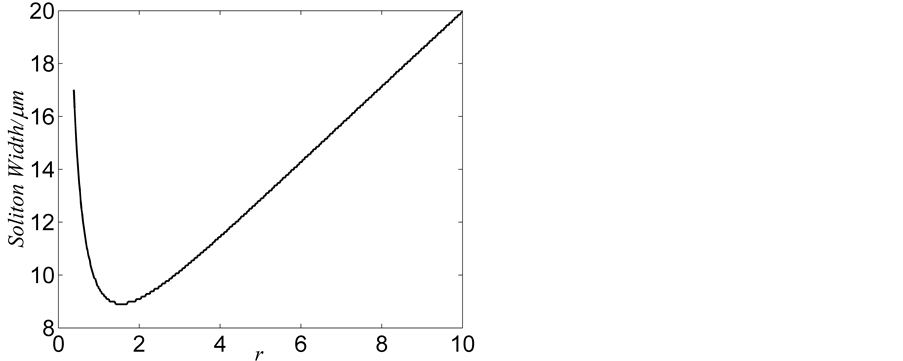
Figure 4. The FWHM of bright PV solitons varies with the ratio of soliton peak intensity to background intensity for
图4.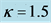 时亮光伏孤子的半高全宽随孤子峰值与背景光比值的变化
时亮光伏孤子的半高全宽随孤子峰值与背景光比值的变化
4. 相干亮光伏孤子的演化特性
LiNbO3晶体为非瞬时非线性介质,对光强分布具有慢时间响应。若入射一束空间非相干信号光,可以看作由一组相干成分组成,各个相干成分相互作用并受非线性效应影响。晶体在信号光和均匀背景光共同作用下,折射率变化可用公式(4)表示。在稳态条件下,非相干光束的演化过程可由下列一组类似耦合非线性薛定谔方程描述 [15] [16] ,
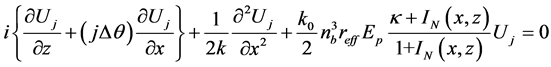 (9)
(9)
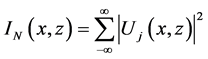 (10)
(10)
方程(9)-(10)中, 为离散的指数(
为离散的指数( ),
),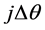 为第
为第 个“相干分量”与传输方向的夹角,
个“相干分量”与传输方向的夹角,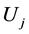 为非相干光束中的分量,即相干密度函数,
为非相干光束中的分量,即相干密度函数,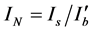 为非相干光束的归一化光强。方程(9)和(10)描述了在
为非相干光束的归一化光强。方程(9)和(10)描述了在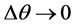 情况下,光伏晶体中非相干光由自散焦向自聚焦转换的物理过程。
情况下,光伏晶体中非相干光由自散焦向自聚焦转换的物理过程。
假定相干密度函数在初始位置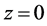 处的表达式为
处的表达式为
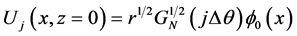 (11)
(11)
其中,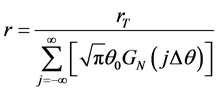 ,
,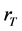 为亮非相干光束的最大光强(即:
为亮非相干光束的最大光强(即: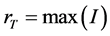 )
)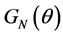 为归一化的非相干光源的角功率谱,
为归一化的非相干光源的角功率谱, 为空间调制函数。
为空间调制函数。
假定非相干光源的归一化角功率谱具有高斯分布形式,即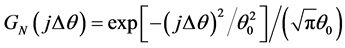 ,其中
,其中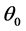 为角功率谱的宽度。在考虑亮非相干空间孤子时,空间调制函数在输入位置取为高斯函数,即
为角功率谱的宽度。在考虑亮非相干空间孤子时,空间调制函数在输入位置取为高斯函数,即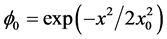 ,
,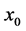 与光束半高宽度(FWHM)之间的关系为
与光束半高宽度(FWHM)之间的关系为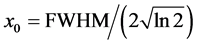 。选择 LiNbO3晶体,参数与图3相同,取
。选择 LiNbO3晶体,参数与图3相同,取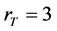 ,光源的角功率谱
,光源的角功率谱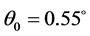 ,
, ,即非相干高斯光束的半高全宽为
,即非相干高斯光束的半高全宽为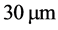 。利用分步傅里叶算法数值模拟方程(10),得到归一化的非相干高斯光在不同
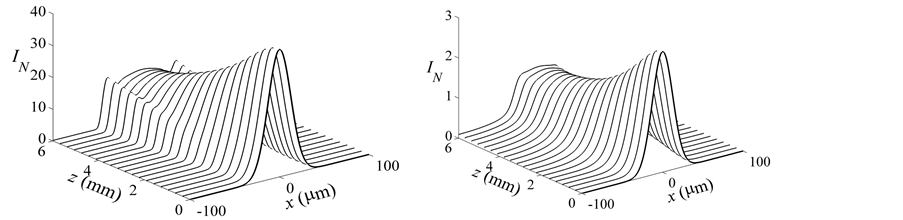
。利用分步傅里叶算法数值模拟方程(10),得到归一化的非相干高斯光在不同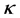 值下的演化曲线,如图5所示。图5(a)为
值下的演化曲线,如图5所示。图5(a)为 时光束的演化过程,信号光传输6 mm后半高宽度在自散焦作用下展宽。若晶体采用一束更短波长的背景光照射晶体,使得
时光束的演化过程,信号光传输6 mm后半高宽度在自散焦作用下展宽。若晶体采用一束更短波长的背景光照射晶体,使得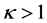 ,则光束自陷效应开始产生。图5(b)和图5(c)分别为
,则光束自陷效应开始产生。图5(b)和图5(c)分别为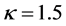 和
和 时光束的演化过程。此时,晶体表现出自聚焦效应,非相干光束中的各相干分量融合在一起,无弯曲向前传输形成稳态的孤子,如图5(c)所示。若
时光束的演化过程。此时,晶体表现出自聚焦效应,非相干光束中的各相干分量融合在一起,无弯曲向前传输形成稳态的孤子,如图5(c)所示。若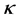 值继续变大,晶体的自聚焦效应更强,光束进一步塌陷。图5(d)为
值继续变大,晶体的自聚焦效应更强,光束进一步塌陷。图5(d)为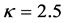 时光束传输的演化图,在此过程中,光束压缩或展宽均有可能。上述现象也与之前非相干孤子的实验观察相吻合。
时光束传输的演化图,在此过程中,光束压缩或展宽均有可能。上述现象也与之前非相干孤子的实验观察相吻合。
现在考虑较高强度比值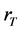 和较大角功率谱宽度
和较大角功率谱宽度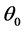 对非相干光传输的影响。图6(a)是非相干高斯光束在
对非相干光传输的影响。图6(a)是非相干高斯光束在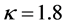 ,
, ,
,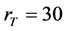 条件下的传输曲线。随着传输距离的增加,高斯光束出现展宽,且具有
条件下的传输曲线。随着传输距离的增加,高斯光束出现展宽,且具有
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 5. Evolution chart of the normalized intensity profile resulting from an incoherent Gaussian beam when its initial FWHM is ,
,  ,
,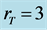 ; (a)
; (a) ; (b)
; (b) ; (c)
; (c)  and (d)
and (d)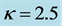
图5. 初始半高宽度为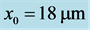 ,
, 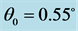 ,
,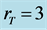 的非相干高斯光束归一化包络演化图;(a)
的非相干高斯光束归一化包络演化图;(a)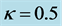 ; (b)
; (b) ; (c)
; (c)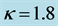 ; and (d)
; and (d)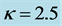
 (a) (b)
(a) (b)
Figure 6. Propagation of an incoherent Gaussian beam in LiNbO3 crystal when the parameters are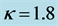 ,
,  , and (a)
, and (a)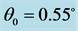 ,
,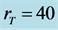 ; (b)
; (b)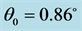 ,
,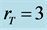
图6. LiNbO3晶体中非相干高斯光束的传输,光束参数为 ,
, 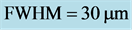 , (a)
, (a) ,
, ; (b)
; (b)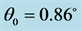 ,
,
不规则性。在相干极限情况下,这一展宽归结为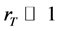 时饱和光折变非线性效应。在数值模拟过程中发现,角功率谱宽度
时饱和光折变非线性效应。在数值模拟过程中发现,角功率谱宽度 对光束传输也具有重要作用。图6(b)描述了
对光束传输也具有重要作用。图6(b)描述了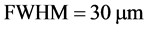 ,
,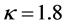 ,
,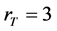 ,和
,和 时非相干高斯光束的传输过程。从图中看到,光束传输6 mm后展宽为类似于矩形形状。总之,在满足图5(c)所形成的亮光伏孤子条件时,若提高强度比值
时非相干高斯光束的传输过程。从图中看到,光束传输6 mm后展宽为类似于矩形形状。总之,在满足图5(c)所形成的亮光伏孤子条件时,若提高强度比值 和角功率谱宽度
和角功率谱宽度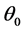 ,均会破坏孤子的形成。如果要克服衍射效应形成孤子,需要背景光提供更大的光伏效应。
,均会破坏孤子的形成。如果要克服衍射效应形成孤子,需要背景光提供更大的光伏效应。
5. 结论
总之,本文理论研究了LiNbO3晶体中一维亮光伏孤子的形成机理以及动态演化特性。通过加载背景光的方法使得自散焦晶体实现自聚焦的转换并形成亮光伏孤子。文章以自散焦LiNbO3晶体为例,计算了折射率空间分布与光伏常数比值 之间的关系,并给出了亮光伏孤子的存在曲线。研究发现,在
之间的关系,并给出了亮光伏孤子的存在曲线。研究发现,在 时,折射率分布类似于凹透镜,可形成暗光伏孤子;在
时,折射率分布类似于凹透镜,可形成暗光伏孤子;在 时,折射率分布类似于凸透镜,可形成亮光伏孤子。该研究结果对无偏压的全光孤子器件设计提供可靠性参考。另外,文章进一步采用相干密度法理论研究了非相干亮光伏孤子在自散焦晶体中的演化特性,并利用分步傅里叶算法数值模拟了不同
时,折射率分布类似于凸透镜,可形成亮光伏孤子。该研究结果对无偏压的全光孤子器件设计提供可靠性参考。另外,文章进一步采用相干密度法理论研究了非相干亮光伏孤子在自散焦晶体中的演化特性,并利用分步傅里叶算法数值模拟了不同 ,强度比值
,强度比值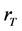 和角功率谱宽度
和角功率谱宽度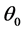 对非相干亮光伏孤子形成的影响。这里
对非相干亮光伏孤子形成的影响。这里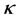 值越大,非线性效应越强,自聚焦效应越明显。在
值越大,非线性效应越强,自聚焦效应越明显。在 较大时或角功率谱宽度
较大时或角功率谱宽度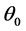 较小时存在调制不稳定。上述研究结果对基于孤子的光器件研究具有一定的理论指导。
较小时存在调制不稳定。上述研究结果对基于孤子的光器件研究具有一定的理论指导。
基金项目
陕西省教育厅项目(No. 16JK2247),西京学院高层次人才专项基金 (No. XJ15B02)。
文章引用
霍广文,陈 恒,张美志. LiNbO3晶体中非相干空间亮孤子的动态演化特性
Dynamics Evolution Characteristic of Incoherent Bright Spatial Solitons in LiNbO3 Crystal[J]. 应用物理, 2016, 06(08): 175-183. http://dx.doi.org/10.12677/APP.2016.68023
参考文献 (References)
- 1. Morin, M., Dree, G., Salamo, G. and Segev, M. (1995) Waveguides Formed by Quasi-Steady-State Photorefractive Spatial Solitons. Optics Letter, 20, 2066-2068. http://dx.doi.org/10.1364/OL.20.002066
- 2. Hao, L.L., Wang, Q. and Hou, C.F. (2014) Spatial Solitons in Biased Photorefractive Materials with both the Linear and Quadratic Electro-Optic Effects. Journal of Modern Optics, 61, 1236-1245. http://dx.doi.org/10.1080/09500340.2014.928379
- 3. Segev, M., Valley, G.C., Bashaw, M.C., Taya, M. and Fejer, M.M. (1997) Photovoltaic Spatial Solitons. Journal of the Optical Society America B, 14, 1772-1781. http://dx.doi.org/10.1364/JOSAB.14.001772
- 4. She, W.L., Lee, K. and Lee, W. (1999) Observation of Two-Dimensional Bright Photovoltaic Spatial Solitons. Physical Review Letters, 83, 3182-3185. http://dx.doi.org/10.1103/PhysRevLett.83.3182
- 5. Taya, M., Bashaw, M.C., Fejer, M.M., Segev, M. and Valley, G.C. (1995) Observation of Dark Photovoltaic Spatial Solitons. Physical Review A, 52, 3095-3100. http://dx.doi.org/10.1103/PhysRevA.52.3095
- 6. Zhang, M.Z., Lu, K.Q., Cheng, G.H., Zhang, L., Kang, Y.-F. and Zhang, Y.-P. (2008) One-Dimensional Waveguides Induced by Photovoltaic Dark Spatial Solitons of Partially Spatially Incoherent Light. Acta Photonica Sinica, 37, 1942-1946.
- 7. Lan, S., DelRe, E., Chen, Z.G., Shih, M.F. and Segev, M. (1999) Directional Coupler with Soliton-Induced Waveguides. Optics Letter, 24, 475-477. http://dx.doi.org/10.1364/OL.24.000475
- 8. Lu, K.Q., Zhao, W., Yang, Y.Y., et al. (2006) Soliton-Induced Waveguides in Photorefractive Photovoltaic Materials. Journal of Modern Optics, 53, 2137-2151. http://dx.doi.org/10.1080/09500340600809145
- 9. Anastassiou, C., Shih, M.F., Mitchell, M., Chen, Z.G. and Segev, M. (1998) Optically Induced Photovoltaic Self-Defocusing-to-Self-Fo- cusing Transition. Optics Letter, 23, 924-926. http://dx.doi.org/10.1364/OL.23.000924
- 10. Liu, S.M., Wang, D.Y., Zhao, H.E., et al. (2002) The Dynamic Conversion from Self-Defocusing to Self-Focusing and the Phase Conjugate Bright Spatial Soliton. Acta Physica Sinica, 51, 2761-2766.
- 11. Wang, D.Y., Liu, S.M., Chen, X.H., et al. (2003) The Influence and Control of Incoherent Irradiation on Photorefractive Nonlinearity of LiNbO3:Fe Crystal. Acta Physica Sinica, 52, 395-400.
- 12. She, W.L., Xu, C.C., Guo, B. and Lee, W.-K. (2006) Formation of Photovoltaic Bright Spatial Soliton in Photorefractive LiNbO3 Crystal by a Defocused Laser Beam Induced by a Background Laser Beam. Journal of the Optical Society America B, 23, 2121-2126. http://dx.doi.org/10.1364/JOSAB.23.002121
- 13. Zhang, M.Z., Lu, K.Q., Cheng, G.H., et al. (2010) One-Dimensional Steady-State Bright Photovoltaic Solitons in LiNbO3:Fe Crystal with Back Ground Illumination. Optik, 121, 575-580. http://dx.doi.org/10.1016/j.ijleo.2008.09.020
- 14. Zhang, M.Z., Huo, G.W., Zhang, Y.Q., Kang, Y. and Duan, Z. (2012) Modulation Instability of Bright Photovoltaic Solitons on a Partially Incoherent Background. Laser Physics, 22, 1295-1300. http://dx.doi.org/10.1134/S1054660X12080178
- 15. Christodoulides, D.N., Coskun, T., Mitchell, M. and Segev, M. (1997) Theory of Incoherent Self-Focusing in Biased Photorefractive Media. Physical Review Letters, 78, 646-649. http://dx.doi.org/10.1103/PhysRevLett.78.646
- 16. Cohen, O., Buljan, H., Schwartaz, T., Fleischer, J.W. and Segev, M. (2006) Incoherent Solitons in Instantaneous Nonlocal Nonlinear Media. Physical Review E, 73, 015601. http://dx.doi.org/10.1103/PhysRevE.73.015601
NOTES
*通讯作者。