Applied Physics
Vol.
12
No.
01
(
2022
), Article ID:
48368
,
13
pages
10.12677/APP.2022.121003
三维燃料组件流阻数值计算研究
汪俊1,符凯2,马佳珍1
1中国核电工程有限公司,北京
2上海积鼎信息科技有限公司,上海
收稿日期:2021年12月20日;录用日期:2022年1月19日;发布日期:2022年1月27日

摘要
燃料组件的阻力特性影响堆芯不同类型组件的流量分配,对堆芯设计的影响不可忽视。为得到更为精确的燃料组件流阻特性并获得对应阻力系数,本文采用分段计算方法针对两种工质条件下的燃料组件进行了单通道三维数值模拟研究。结果表明:不同工质下,随着进口速度上升,各计算域局部压降及总压降均增大;不同工质下,对于三种形式的底板阻力系数D,四孔底板最小,圆孔底板最大,Phi孔底板介于前两者之间。最后还获得了工质分别为水和空气时燃料组件区和不同形式底板区的阻力系数,为稳态多孔介质模型中计算表征多孔介质影响的源项S提供了参考,对燃料组件通道的三维数值模拟提供了指导意义。
关键词
燃料组件,数值模拟,阻力系数

Study on Numerical Calculation of Flow Resistance of Three-Dimensional Fuel Assembly
Jun Wang1, Kai Fu2, Jiazhen Ma1
1China Nuclear Power Engineering Co., Ltd., Beijing
2Shanghai Jiding Information Technology Co., Ltd., Shanghai
Received: Dec. 20th, 2021; accepted: Jan. 19th, 2022; published: Jan. 27th, 2022

ABSTRACT
The flow resistance characteristics of fuel assemblies affect the flow flux distribution of the different types of assemblies in the core, and its influence on the core design cannot be ignored. In order to obtain more accurate flow resistance characteristics and corresponding resistance coefficient of fuel assemblies, a single channel three-dimensional numerical simulation of fuel assemblies under two working fluids is carried out by using the domain division technique. The results show that with the increase of flow velocity of the inlet, the local pressure drop and total pressure drop in each calculation domain increase. Under different working fluids, for the three types of bottom plate resistance coefficient D, four holes bottom plate is the smallest, round hole bottom plate is the largest, and Phi hole bottom plate is between the first two. Meanwhile, the resistance coefficients of the fuel assembly area and different types of bottom plate areas are obtained when the working fluids are water and air respectively, which provides a reference for calculating the source term S representing the influence of porous media in the steady-state porous media model and provides a guiding significance for the three-dimensional numerical simulation of fuel assembly channels.
Keywords:Fuel Assembly, Numerical Simulation, Resistance Coefficient

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
燃料组件是核电站的核心部件之一,在役运行的核电站中燃料成本占总运行成本的近30%,研发具有高燃耗、低破损、长循环、高可靠性和良好热工水力性能等优点的先进燃料组件,是世界各大核电公司、机构改善核电站安全性、可靠性和经济性的有效手段,也是我国核电国产化的关键。燃料组件由燃料棒和定位格架组成复杂的开式通道,系统掌握燃料组件中的流场行为特性,建立合理的阻力特性计算方案,是优化其热工水力性能的关键一步,也是建立燃料组件设计评价体系,突破先进燃料组件自主设计技术的重要基础。
Holloway等 [1] [2] 开展了不同雷诺数下5 × 5棒束单相传热实验,通过压降测量确定了格架压力损失系数和特征损失系数。Govindha等 [3] [4] 研究发现通道内流量分配对摩擦阻力系数产生影响。李继威等 [5] 开展燃料组件上下管座压降试验获得了阻力系数及其测量不确定度。李勇等 [6] 基于雷诺数相似准则通过实验研究燃料组件在铅基合金冷却剂中的阻力特性,获得一定雷诺数范围内摩擦因子随Re变化的关系式。杜语聪 [7] 等应用不同摩擦阻力计算公式对组件模型进行模拟计算,通过对比燃料组件摩擦阻力压降、流速分布以及温度分布的计算结果和实验结果,确定了计算性能最佳的燃料组件摩擦阻力计算公式。晁嫣萌等 [8] [9] 利用CFX对棒束通道热特性进行了数值模拟,分析了多种典型湍流模型对燃料组件压降及换热特性数值结果的影响。Péniguel等 [10] 对钠冷快堆冷却剂的三维流动特性和耦合传热进行了分析,但缺乏对局部压力分布及整体压降的模拟计算。燃料组件总压降由各部件局部压降叠加得到。魏宗岚等 [11] 基于CFD对燃料组件上管座的阻力特性进行了分析和评价,说明了阻流塞是实验测量结果与参考数据存在差异的主要原因,并给出了上管座阻力系数的取值建议,上述相关研究都是对燃料组件各部分进行单独研究,关于燃料组件全组件的流阻特性计算研究还较少。杨红义等 [12] 对燃料区6类燃料组件中的两类进行模块式及整体式三维数值模拟,获得了两类组件的流阻特性,并深入研究了流速及温度变化对流阻特性的影响。因此,为得到更为精确的燃料组件流阻特性并获得对应阻力系数,对不同工质条件下的燃料组件进行三维数值模拟研究至关重要。
本文采用分段计算方法对某燃料组件进行单通道数值模拟。获得工质分别为水和空气时燃料组件区及底板区压降及流阻特性,通过分析压降与进口速度对应关系,深入研究获得不同工质下燃料组件区和不同形式底板区的阻力系数,为稳态多孔介质模型中计算表征多孔介质影响的源项S提供了参考,对燃料组件通道的三维数值模拟提供了指导意义。
2. 几何模型及计算域划分
2.1. 几何模型
计算区域为燃料组件单通道部分,主要包括上管座、下管座、端部格架(2个)、大格架(6个)和小格架(3个)、导向管和燃料棒,如图1所示。
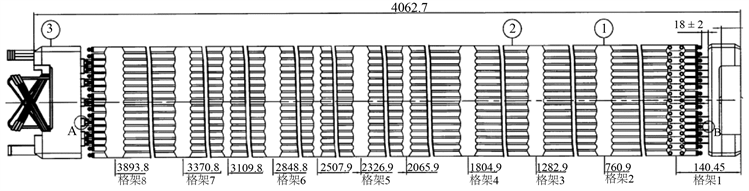
Figure 1. Schematic diagram of fuel assembly and its skeleton
图1. 燃料组件及其骨架示意图
2.2. 计算域划分
由于整个燃料组件结构复杂,网格量巨大,整体计算困难,M.A. Navarro等 [13] 于2011年采用了分段计算方法(DDT)计算了5 × 5的某格架上下游流动。其策略是将燃料组件沿z方向切割成若干块,分别对每块进行计算,上游计算域的出口对应下游计算域的进口。结果表明:在分区计算后,格架下游的压降比未分区时略高,但在可以接受的范围之内。
因此,结合实际模型和分段计算方法,对整个燃料组件进行如下计算,设计以下六种计算域:
1) 大格架与小格架联合计算域
2) 大格架计算域
3) 小格架计算域
4) 上管座联合端部格架计算域
5) 下管座联合端部格架计算域
6) 充分发展棒束区
对于各个部件,计算各区域的局部压降 。对于燃料组件棒束区,计算压降梯度 ,再乘以格架区和管座区之外的棒束长度,得到对应棒束区压降。这里的压降对应于某棒束充分发展区的压降。最后将各区域的局部压降叠加,得到整个燃料组件单通道区的总压降。
2.3. 棒束区入口段长度的确定
在流体流经格架后到达棒束区,经历一段距离后,其速度三个分量沿z方向不再变化时,我们认为流体已经进入充分发展区。
在确定棒束区流动达到充分发展所需的入口段长度时,主要考察棒束区流速沿z方向的发展。计算域的入口边界为均匀分布的速度场U = (0 0 0.068) m/s。出口边界的平均动压设为0。在棒束间流道内取A、B两点,其中A点靠近中央的导向管,B点靠近边缘的燃料棒,如图2所示。绘制A、B两点处z方向速度分量沿z轴变化图,如图3所示。

Figure 2. Position of points A and B in the flow cross section between rod bundles
图2. 棒束间流道内A、B点在流动横截面的位置

Figure 3. Variation of z-direction velocity component along z-axis at points A and B
图3. A、B点处z向速度分量沿z轴变化
由图可以确定,Re = 800时,棒束区流体充分发展所需入口段长度约为0.15 m。由于入口段长度L满足
(1)
式中,DH为水力直径。
对于雷诺数相同的流动,满足相似定律时入口长度应当接近。因此在工质为空气和水时,对于雷诺数相同的工况,认为其流动相似,入口段长度接近。而对于Re < 800的流动,流体在棒束间流动达到充分发展所需的距离更短。因此,在计算格架区压降时,下游所取的棒束区长度应大于0.15 m。
2.4. 格架区上游棒束长度的确定
在流体靠近格架时,流体减速导致局部高压区产生。入口位置应远离该局部高压区。由于大格架、小格架和端部格架下沿处几何形状类似,为了简化计算,这里只考察小格架上游至下游段的流场压力变化,以确定格架区局部高压区的范围。计算域中小格架上游的棒束区被加长到55 mm,入口速度为均匀分布的速度场U = (0 0 0.068) m/s充分发展后得到的速度分布,出口的平均动压值设为0。对图2中A、B两点动压p进行采样,得到A、B点处动压沿z方向的分布如图4所示。

Figure 4. Dynamic pressure p changes along the z-axis at points A and B
图4. A、B点处动压p沿z轴变化
由图看出,从入口流入该区域的流体由于已经充分发展,因此在远离格架的上游区域内动压p呈线性下降的趋势。流经A点的流体在接近小格架下沿时,遇到障碍速度下降,局部动压突然升高;流入至小格架栅板间后,流道突然变窄,A、B点处速度均增加,动压p陡降;流体进入小格架区内部时先稍许加速而后减速;流出小格架后,流道扩张,略微减速,动压p略微上升后再次下降。可以发现对于采用充分发展的速度入口时,小格架上游的影响域比较小,主要集中在格架下沿附近15 mm的区域内。为保险起见,格架区的入口棒束区长度至少取30 mm。
3. 数值计算方案
3.1. 阻力模型
采用OpenFOAM软件对燃料组件进行单通道数值模拟。在整池网格生成脚本中,套筒内部的单通道由于几何过于复杂,无法进行细致网格划分,因而对于每个单通道内部,均采用多孔介质模型进行近似计算。稳态多孔介质模型的质量方程为
(2)
动量方程为
(3)
其中源项S表征多孔介质的影响。
(4)
式中,S表达式中的前后两项分别为多孔介质对流体的粘性阻力和惯性阻力。公式中 表示流体密度, 表示孔隙率,全多孔区域中假定为常数, 表示粘性系数, 表示渗透率,C2表示惯性阻力因子。
源项S的计算需要阻力系数D和F。两者在具体计算时依赖于压降梯度,如下式。
(5)
其中,ΔP/L为压降梯度,Vs为流体表面速度。通过比较各项系数可得
(6)
因此,阻力系数D和F的计算需要通过若干组数值实验求得单通道区平均压降,拟合出形如式(5)的二次曲线。
3.2. 网格划分及无关性验证
根据结构的不同特性,采用专业前处理软件Ansa对燃料组件各区域进行网格划分,全区域的体网格以四面体非结构网格为主。考虑到单通道区内部流动对应的Re数很低(最多不超过200),根据文献 [1] 中所述,Re数小于900时,格架区的流动为层流。进出口面呈正方形,中间挖去燃料棒与导向管截面,如图5所示。
由于流体流动时会绕过栅板及搅浑翼,在生成网格时栅板厚度方向以及搅浑翼厚度方向需生成至少两层网格,以确保计算时良好的收敛性,如图6。
上下管座区网格的生成过程与格架区类似。管座与棒束区有一段为导向管,导向管的面网格可通过拉伸棒束区导向管的截面与管座融合得到。下管座的防异物板区的面网格同样需要在厚度方向生成两层网格。

Figure 5. Mesh of inlet and outlet surface
图5. 进出口面网格
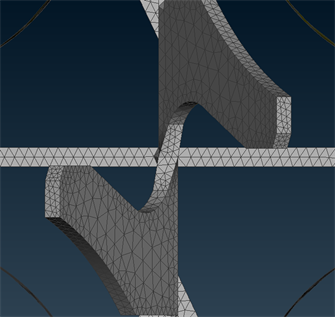
Figure 6. Grid of grid plate and muddy wing
图6. 栅板与搅浑翼的网格
为提高计算精度,采用缩小棒束面网格尺寸为标准网格的50%并同时缩小进出口棒束空隙间的面网格尺寸的加密方式对端部格架区的网格进行了加密,获得共三套网格方案。
为确保网格划分的可靠性,在Re = 800时,对不同网格方案以端部格架两个端面间的平均压差为标准,进行网格无关性验证,结果如表1所示。
Table 1. Grid independence verification
表1. 网格无关性验证
由表1可知,随着网格数量增加,端部格架两个端面间的平均压差趋于稳定。当网格数达到中等疏密时,其计算所得端部格架两个端面间的平均压差随网格数增加的量小于0.2%。兼顾计算效率与精度,最终选择中等疏密程度的网格生成方案。经过网格质量验证,计算域各部分网格的边长比、正交性和面积比均符合OpenFOAM软件的要求。
3.3. 边界条件及收敛判据
关于边界条件,在计算压降时,流体从各个部件区的底部流入,从上部出口流出。计算域的边界条件设定如表2所示。
工质分别为水和空气时的进口速度取值如表3所示,分别取八个数值进行模拟,对应雷诺数100~800,在该雷诺数范围工况下,格架区的流动均未进入转捩区。
采用标准不可压求解器simpleFoam计算各部件区的动压和速度,组件格架区的流体采用层流模型,底板区的流体采用湍流模型。流动介质为水时,ν = 1.01e−6 m2/s;流动介质为空气时,ν = 1.5e−5 m2/s。收敛时速度各分量残差不高于1e−3,动压p残差不高于1e−3。
Table 2. Boundary conditions
表2. 边界条件
其中,p = P/ρ,p为动压(kinematic pressure),P是流体的压力,ρ为流体密度。
Table 3. Inlet velocity under different working conditions when the working medium is water and air
表3. 工质为水和空气时不同工况进口速度
4. 计算结果分析与讨论
4.1. 压降计算及分析
4.1.1. 燃料组件区压降
为计算部件区的局部压降,利用OpenFOAM中的后处理模块pressure Difference Patch计算得到进口和出口间的平均动压差。其中面平均压力根据下式进行计算
(7)
其中,Ai为各个网格单元的面积,pi为各个单元内的动压。
根据格架的数量及分布,燃料组件区的总压降可通过下式计算。
(8)
其中,ΔPsum为燃料组件区总压降,ΔPBS为大格架区压降,ΔPSS为小格架区压降,ΔPB&S为大小格架联合区域压降,ΔPTL为上管座联合端部格架区域压降,ΔPLB为下管座联合端部格架区域压降,ΔProd/Lrod为棒束区压降梯度,Lot为格架区和管座区之外的棒束长度,ΔProd为棒束区压降。
工质为水和空气时计算得到的各计算域局部压降及总压降数据分别如图7、图8所示。可以看出,不同工质下,随着雷诺数从100增至800,即进口速度上升,各计算域局部压降及总压降均增大,其中局部压降占比最大为棒束区压降,棒束区压降占总压降比值逐渐减小,工质为水时压降比值从0.34减小至0.22;工质为空气时压降比值从0.33减小至0.21,即棒束区损失减小。

Figure 7. Calculation results of different working conditions when the working medium is water
图7. 工质为水时不同工况的计算结果
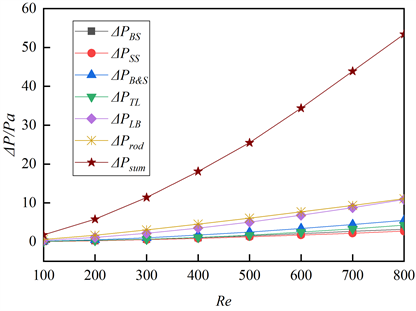
Figure 8. Calculation results of different working conditions when the working medium is air
图8. 工质为空气时不同工况的计算结果
4.1.2. 底板区压降
因底板区的几何参考长度较大,流动的雷诺数较高,且流过底板孔的流体存在不稳定的涡结构,所以在计算底板区的压降时采用了湍流模型计算流场。流体在垂直流向底板时,z向速度分量为0,尤其对于中心未开孔的四孔底板,底板的近壁面区耗散很大。对于此区域,k-ε模型中的耗散项在建模时存在局限性,已经无法描述此区域的湍流行为。而k-ω SST模型在近壁面区采用k-ω模型进行建模,远离壁面区采用k-ε模型,可以有效避免ε在近壁面域增长失控。
取三种形式底板分别为Phi孔底板、圆孔底板和四孔底板,工质为水和空气时各雷诺数下流动参数及计算得到的各形式底板压降分别如表4和图9所示。由图9可以看出,不同工质下,四孔底板压降均最大,圆孔底板次之,Phi孔底板最小。随着雷诺数增大,各形式底板压降均增大,即底板损失增大。

Figure 9. Pressure drop in floor area under different working conditions with different working medium
图9. 不同工质时不同工况底板区压降
Table 4. Flow parameters in floor area under different working conditions with different working medium
表4. 不同工质时不同工况底板区流动参数
4.2. 阻力系数计算及分析
4.2.1. 燃料组件区阻力系数
分别拟合工质为水和空气时总压降与z方向速度分量W得到二次曲线,如图10和图11所示。燃料组件总长L为4.062 m,通过2.1节公式(5)计算可得渗透率α和惯性阻力因子C2,进而求得对应阻力系数D和F,拟合二次曲线及求得各参数值如表5所示。
Table 5. Values of each parameter are obtained by fitting when the working medium is water and air
表5. 工质为水和空气时拟合求得各参数值
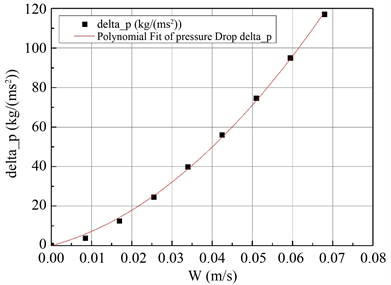
Figure 10. Fitting curve of total pressure drop and velocity in single channel region when working medium is water
图10. 工质为水时单通道区总压降与速度拟合曲线

Figure 11. Fitting curve of total pressure drop and velocity in single channel area when working medium is air
图11. 工质为空气时单通道区总压降与速度拟合曲线
根据文献 [14],空气粘性阻力系数SLAM与形状阻力系数Σk的计算公式如下。
(9)
(10)
其中粘性阻力系数SLAM与层流压降的主要组成部分有关,形状阻力系数Σk与层流压降的次主要组成部分有关。
(11)
(12)
a1与a2为压降梯度公式中速度项的系数,DH,Ref为水力直径。
(13)
结合表5中压降梯度二次曲线可得单通道燃料组件全域的平均阻力因子。
(14)
这里Σk的计算值接近于文献 [14] 中的实验计算值30.6,而SLAM比文献 [12] 中的值132.9要低,这是因为实验所采用的单通道燃料组件模型在实验中被外围套筒所包围,并且它的格架数目更多(9个大格架,10个小格架,2个端部格架)。燃料组件外围的套筒与多出的格架引起的摩擦压降使得实验中燃料组件的粘性阻力因子更大。
4.2.2. 底板区阻力系数
对于三种形式的0.03 m厚的底板,即Phi孔底板、圆孔底板和四孔底板。根据类似于3.2.1节单通道燃料组件区的阻力系数计算方法可得底板区阻力系数如表6所示。
Table 6. Resistance coefficients of each floor when the working medium is water and air
表6. 工质为水和空气时各底板阻力系数
由表可知,不同工质下,对于三种形式的底板阻力系数D,四孔底板最小,圆孔底板最大,Phi孔底板介于前两者之间。
5. 结论
本文采用数值模拟方法对单通道燃料组件各区域压降及总压降进行了计算,采用了分段计算方法避免了全区域燃料组件的计算,大大降低了单次计算的网格量,也避免了对格架过分简化。获得如下主要结论:
1) 确定了单个计算域格架下游的棒束区长度,对格架纵向分布的设计具有指导意义。格架之间的纵向距离应大于该流速下的棒束区充分发展长度。若两格架安放的纵向距离小于该流速下对应的充分发展长度,那么流经格架的总压降将会偏低。
2) 不同工质下,随着进口速度上升,各计算域局部压降及总压降均增大,其中局部压降占比最大为棒束区压降,棒束区压降占总压降比值逐渐减小。工质为水时压降比值从0.34减小至0.22;工质为空气时压降比值从0.33减小至0.21,即棒束区损失减小。
3) 获得了工质分别为水和空气时燃料组件区和不同形式底板区的阻力系数,为稳态多孔介质模型中计算表征多孔介质影响的源项S提供了参考,对燃料组件通道的三维数值模拟提供了指导意义。
4) 不同工质下,对于三种形式的底板阻力系数D,四孔底板最小,圆孔底板最大,Phi孔底板介于前两者之间。
文章引用
汪 俊,符 凯,马佳珍. 三维燃料组件流阻数值计算研究
Study on Numerical Calculation of Flow Resistance of Three-Dimensional Fuel Assembly[J]. 应用物理, 2022, 12(01): 15-27. https://doi.org/10.12677/APP.2022.121003
参考文献
- 1. Holloway, M.V., Mcclusky, H.L., Beasley, D.E., et al. (2003) The Effect of Support Grid Features on Local, Single-Phase Heat Transfer Measurements in Rod Bundles. Proceedings of the ASME 2003 Heat Transfer Summer Conference, American Society of Mechanical Engineers, 547-560. https://doi.org/10.1115/HT2003-47433
- 2. Holloway, M.V., Beasley, D.E., Conner, M.E., et al. (2008) Single-Phase Convective Heat Transfer in Rod Bundles. Nuclear Engineering & Design, 238, 848-858. https://doi.org/10.1016/j.nucengdes.2007.08.003
- 3. Govindha Rasu, N. (2014) Thermal Hydraulic Effect of Porous Blockage in Fuel Subassembly of Sodium Cooled Fast Reactor. Annals of Nuclear Energy, 70, 612-616. https://doi.org/10.1016/j.anucene.2014.01.045
- 4. Govindha Rasu, N. (2014) Simultaneous Development of Flow and Temperature Fields in Wire-Wrapped Fuel Pin Bundles of Sodium Cooled Fast Reactor. Nuclear Engineering and Design, 267, 44-60. https://doi.org/10.1016/j.nucengdes.2013.11.066
- 5. 李继威, 干富军, 郑轶雄, 张朝柱, 朱丽兵, 顾汉洋. 燃料组件管座压降试验研究[J]. 动力工程学报, 2016, 36(3): 242-246.
- 6. 李勇, 吕科锋, 陈刘利, 高胜, 黄群英. 铅基研究堆燃料组件阻力特性模拟实验与分析[J]. 核安全, 2017, 16(1): 70-81.
- 7. 杜语聪, 丁常富, 薛新强. 低雷诺数绕丝组件摩擦阻力研究[J]. 华北电力大学学报(自然科学版), 2021, 48(6): 119-126.
- 8. 晁嫣萌, 杨立新, 张玉相, 等. 湍流模型对5×5格架棒束通道流动传热数值模拟影响分析[J]. 原子能科学技术, 2014, 48(10): 1782-1789.
- 9. 晁嫣萌. 定位格架对燃料组件流动传热特性影响的数值模拟研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2015.
- 10. Péniguel, C., Rupp, I., Juhel, J.P., et al. (2009) Three Dimensional Conjugated Heat Transfer Analysis in Sodium Fast Reactor Wire-Wrapped Fuel Assembly. Proceedings of ICAPP’09, Tokyo, 9-311.
- 11. 魏宗岚, 杜思佳, 王啸宇, 吴广皓, 刘松涛, 张渝. 基于CFD的燃料组件上管座阻力特性数值模拟研究[J]. 核动力工程, 2017, 38(S2): 29-33.
- 12. 杨红义, 周志伟, 林超, 李淞, 王予烨. 堆芯燃料组件流阻特性模块式与整体式三维数值模拟方案比较[J]. 原子能科学技术, 2020, 54(5): 908-915.
- 13. Navarro, M.A. and Santos, A.A.C. (2011) Evaluation of a Numeric Procedure for Flow Simulation of a 5×5 PWR Rod Bundle with a Mixing Vane Spacer. Progress in Nuclear Energy, 53, 1190-1196. https://doi.org/10.1016/j.pnucene.2011.08.002
- 14. Lindgren, E.R. and Durbin, S.G. (2013) Laminar Hydraulic Analysis of a Commercial Pressurized Water Reactor Fuel Assembly. US Nuclear Regulatory Commission, Washington DC.
