Computer Science and Application
Vol.06 No.10(2016), Article ID:18828,10
pages
10.12677/CSA.2016.610074
Decision Tree Analysis for Inconsistent Decision Tables
Meiling Xu, Ying Qiao, Jing Zeng, Yuchang Mo, Farong Zhong
College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua Zhejiang

Received: Oct. 5th, 2016; accepted: Oct. 23rd, 2016; published: Oct. 28th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Decision tree is a widely used technique to discover patterns from consistent data set. But if the data set is inconsistent, where there are groups of examples with equal values of conditional attributes but different decisions (values of the decision attribute), then to discover the essential patterns or knowledge from the data set is challenging. Based on the greedy algorithm, we propose a new approach to construct a decision tree for inconsistent decision table. Firstly, an inconsistent decision table is transformed into a many-valued decision table. After that, we develop a greedy algorithm using “weighted sum” as the impurity and uncertainty measure to construct a decision tree for inconsistent decision tables. An illustration example is used to show that our “weighted sum” measure is better than the existing “weighted max” measure to reduce the size of constructed decision tree.
Keywords:Data Mining, Inconsistent Decision Table, Many-Valued Decision, Greedy Algorithm

非一致决策表的决策树分析
许美玲,乔 莹,曾 静,莫毓昌,钟发荣
浙江师范大学数理与信息工程学院,浙江 金华

收稿日期:2016年10月5日;录用日期:2016年10月23日;发布日期:2016年10月28日

摘 要
决策树技术在数据挖掘的分类领域中被广泛采用。采用决策树从一致决策表(即条件属性值相同的样本其决策值相同)中挖掘有价值信息的相关研究较为成熟,而对于非一致决策表(即条件属性值相同的样本其决策值不同)采用决策树进行数据挖掘是当前研究热点。本文基于贪心算法的思想,提出了一种非一致决策表的决策树分析方法。首先使用多值决策方法处理非一致决策表,将非一致决策表转换成多值决策表(即用一个集合表示样本的多个决策值);然后根据贪心选择思想,使用不纯度函数和不确定性相关指标设计贪心选择策略;最后使用贪心选择设计决策树构造算法实现决策树构造。通过实例说明了所提出的权值和贪心选择指标能够比已有的最大权值贪心选择指标生成规模更小的决策树。
关键词 :数据挖掘,非一致决策表,多值决策,贪心算法

1. 引言
一致决策表或单值决策表指的是在给定的决策表中样本的条件属性值相同,并且决策值也相同。但是在实际情况下所分析的数据更多的是非一致决策表,即决策表中样本的条件属性值相同但决策值不同。
对于非一致决策表,一个样本具有多个决策值,目标是为每个样本找出一个决策值。该方法适用于典型的优化问题 [1] ,从多种优化方案中选择一种,并得到其优化结果。在文献 [2] 中,具有多个决策值的决策表通常被称为多标签决策表。在现实世界中多标签决策表无处不在,例如图像视频的语义标注,音乐的情感分析,基因组的功能分类以及文本分类等。多标签决策表的数据分类问题有两种解决方法,一种是通过修改常用的分类方法来处理多标签决策表;另一种是把多标签决策表转换为单标签决策表,然后使用分类算法处理这些数据。这些方法都是通过把整个决策集分成相关决策集和不相关决策集两部分,从而处理决策表的非一致问题,目的是找到预测样本的相关决策集。此外,我们还可以采用学习的方法处理非一致数据问题,如局部学习 [3] 、模糊学习 [4] 、多类标学习 [5] 。由于每个样本都具有多个类标,但只有一个类标是正确的,因此该方法的问题是如何找到正确类标。在局部学习和多类标学习中采用概率方法来处理,在模糊学习中采用标准排序方法来处理。
本文基于贪心算法 [6] 的思想,提出了一种非一致决策表的决策树分析方法。贪心策略是指从问题的初始状态出发,通过若干次的贪心选择而得出最优值(或较优解)的一种解题方法。贪心算法就是从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快地求得更好的解。当达到算法中的某一步不能再继续前进时,算法停止。这时就得到了问题的一个解,但不能保证求得的最后解是最优的做一种目前最贪婪的行动。本文首先使用多值决策方法处理非一致决策表,将非一致决策表转换成多值决策表;然后根据贪心选择思想,使用不纯度函数和不确定性相关指标设计贪心选择策略;最后使用贪心选择设计决策树构造算法实现决策树构造。在该方法中,我们假设每条记录对应的决策都是正确的;并且可以从整个决策集而不是相关决策集中找到一个决策 [7] 。
本文剩余部分组织如下:第二节介绍多值决策表的构造;第三节提出决策树构造方法;第四节进行实例说明,并比较由不同的不纯度函数构造的决策树的大小;最后一节总结全文并介绍下一步工作。
2. 多值决策表构造
在分析非一致决策表时,可以把它们转换为已有的决策表。例如在粗糙集理论 [8] 中,广义决策(generalized decision, GD)可以处理非一致数据问题。通过把一个非一致决策表转换成一个多值决策表,决策集中的决策值分别用不同的数字表示,相同的决策集用相同的数字表示,如由决策表T0 (表1)转换而成的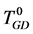 (表2)。另一种方法是使用常用决策 [9] (the most common decision, MCD)来处理这类问题,常用决策的概念来自于使用常用值替代缺失值 [10] 。考虑条件属性值均相同的一组样本中的一个样本,该样本的决策值用样本组中的常用决策表示,如表3中
(表2)。另一种方法是使用常用决策 [9] (the most common decision, MCD)来处理这类问题,常用决策的概念来自于使用常用值替代缺失值 [10] 。考虑条件属性值均相同的一组样本中的一个样本,该样本的决策值用样本组中的常用决策表示,如表3中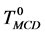 所示。
所示。
和GD,MCD方法不同,本文使用多值决策(many-valued decision, MVD)方法处理非一致决策表,将非一致决策表转换成多值决策表 [2] (即用一个集合表示样本的多个决策值)。考虑条件属性值均相同的一组样本中的一个样本,并且用集合表示该样本的多个决策值,即决策属性集,我们把这样的决策表称为多值决策表,如表4中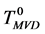 所示。
所示。
一个多值决策表T用一个矩形表示,每一列表示条件属性f1,…,fn,每一行用非负整数表示对应的条件属性值。如果是字符串类型的属性值,那么将其转为非负整数。不出现相同的样本(即不出现重复的行),样本的多个决策用一个非空有限集合表示,如表5所示。N(T)表示T中样本的数量(即行数)。
从决策表T中删除一些样本后得到的表称为T的子表,子表用T(fi1, a1)…(fim, am)表示,fi1,…,fim表示条件属性,a1,…,am表示对应的条件属性值。例如,在表6中子表T(f1, 1)由表5中的第1、2、3个样本组成。同样,表7中子表T(f1, 1) (f2, 1)由表5中的第1、3个样本组成。
如果一个决策属于决策表T中所有决策集,那么称这个决策为决策表T的公共决策,如表7中子表T(f1, 1) (f2, 1)的公共决策是3。如果决策表T没有任何样本或者有一个公共决策,那么称这个决策表为退化表,如表8所示。
E(T)表示决策表T中条件属性值非一致的属性集合。例如,在决策表T中,E(T) = {f1, f2, f3}。同样,在子表T(f1, 1)中,E(T(f1, 1)) = {f2, f3},因为在T(f1, 1)中,属性f1的值是一致的。对于fi ∈E(T),E(T, fi)表示决策表T中条件属性fi对应的属性值集合。例如,决策表T中条件属性f1对应的属性值集合表示为E(T, f1) = {0, 1}。
决策表T中,出现次数最多并且数值最小的决策称为最常用决策。例如,决策表T(f1, 1)中最常用决策是1。因为决策1,3在决策集中都出现了两次但1在数值上是最小的,所以1是最常用决策。Nmcd(T)表示决策表T中包含最常用决策的样本数量。
3. 多值决策表构造
在由多值决策表T构造的决策树中,每个叶子节点代表一个决策(一个自然数),每个非叶子节点代表条件属性集合{f1, …, fn}中的一个属性,每个非叶子节点有多条边(即每个条件属性具有多个属性值)。例如,二元属性有两条边,分别用0和1表示。
Γ表示决策表T构造的决策树,v表示Γ的节点。T(v)表示T的子表,如果v是决策树的根节点,那么T(v) = T,否则T(v)就是决策表T的子表T(fi1,δ1)…(fim,δm),条件属性为fi1,…,fim对应的属性值为δ1,…,δm,分别代表从根节点到节点v整条路径上的节点和边。决策树Γ满足以下条件:
1) 如果T(v)是退化表,那么节点v用公共决策标记。
2) 如果T(v)不是退化表,那么节点v用fi标记,fi∈E(T(v)),如果E(T(v), fi) = {a1, …, ak},那么节点v有k条边,分别用a1,…,ak表示。
例如,图1是由一个多值决策表构造的决策树。如果节点v用一个非叶子节点f3标记,那么与v对应的子表T(v)就是T(f1, 0)。同样,与叶子节点2对应的子表是T(f1, 0) (f3, 1),并且2是公共决策。
在贪心算法中,我们需要选择合适的属性将决策表分区,即形成更小的子表,直到我们得到可以用于标记叶子节点的退化表。不纯度函数用于计算当前分区的不确定性,不纯度函数值越小,则表示该分
Table 1. Decision table T0
表1. 决策表T0
Table 2. Decision table
表2. 决策表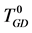
Table 3. Decision table
表3. 决策表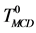
Table 4. Decision table
表4. 决策表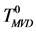
Table 5. A many-valued decision table T
表5. 多值决策表T
Table 6. A subtable of many-valued decision table T
表6. 子表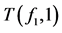
Table 7. A subtable of many-valued decision table T
表7. 子表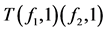
Table 8. A degenerate many-valued decision table
表8. 退化表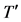
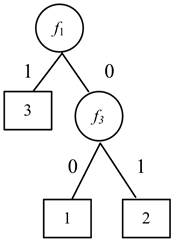
Figure 1. Decision tree for the many-valued decision table
图1. 多值决策表构建的决策树
区的不确定性越小,即分区质量越高。我们使用不纯度函数来评估分区的质量,从而选择合适的分区构造决策树。通过计算分区的不确定性指标,从而计算不纯度函数。如果有一个公共决策,那么不确定性指标为0。
1) 不确定性指标:不确定性指标U是从非空多值决策表集合到真实数值集合的函数,因此,U(T) ≥ 0,当且仅当是退化表时,U(T) = 0。我们选择错分误差 [11] 作为不确定性指标。
错分误差:me(T) = N(T) − Nmcd(T),N(T)表示T中样本的数量(即行数),Nmcd(T)表示决策表T中包含最常用决策的样本数量。计算决策表T中所有样本数量和包含最常用决策样本数量之间的差值。
2) 不纯度函数:U是一个不确定性指标,fi∈E(T), E(T, fi) = {a1, …, at},属性fi把决策表T分成t个子表:T1 = T(fi, a1), …, Tt = T(fi, at)。我们将不纯度函数做如下定义:
权值和: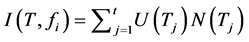
根据多值决策表,采用贪心策略、自顶向下递归构造决策树。首先初始化决策树,用决策表标记根节点,然后判断决策表的不确定指标是否为0,如果不确定指标为0,则用决策表中的公共决策代替决策表标记根节点;如果不确定指标不为0,则计算决策表中每个条件属性对应的不纯度函数,选择函数值最小的属性,当函数值相同时,选择下标最小的属性,将其作为分裂节点,并代替决策表标记根节点,根据所选属性的属性值创建节点,各个节点用对应的子表标记,分裂节点到各个节点上的边用对应的属性值表示,按上述步骤递归创建决策树各个节点。当树中所有节点都没有用表标记时,停止树的构造,输出决策树。
具体的决策树构造算法如表9所示。
4. 决策树构造实例
本节通过实例(见表10)分析说明本文所提出的基于权值和指标贪心选择策略的决策树分析过程,并和已有文献 [4] 中所采用的基于最大权值指标贪心选择策略的决策树分析过程进行比较。
首先创建决策树G的根节点,并用表T标记该节点,然后自顶向下循环创建决策树各个节点。第一次循环中,选择的子表T′为表T,即T′ = T,树G中只有一个根节点v,所以用T′标记节点v。因为U(T′) ≠ 0,所以对于每个fi,fi∈E(T′) = {f1, f2, f3},使用表10中的数据分别计算不纯度函数I(T′, f1)、I(T′, f2)、I(T′, f3)的值,通过计算可知,I(T′, f1) = 41,I(T′, f2) = 38,I(T′, f3) = 47,I(T′, f2)值最小,用f2代替T′标记节点v,对于每个δ,δ ∈E(T′, f2) = {0, 1, 2},在树G中加入节点v0,v1,v2,分别与连接节点v相连并将边标记为0,1,2,分别用子表T(f2, 0),T(f2, 1),T(f2, 2)标记节点v0,v1,v2,结果如图2所示。
然后从子表T(f2, 0),T(f2, 1),T(f2, 2)中选择一个子表,比如选择T(f2, 0)即T′ = T(f2, 0)。因为U(T′) ≠ 0,所以对于每个fi,fi∈E(T′) = {f1, f3},使用表11分别计算不纯度函数I(T′, f1)、I(T′, f3)的值,通过计算可知,I(T′, f1) = 0,I(T′, f3) = 0,但是i值取最小,所以选择f1,用f1代替T′标记节点v0,对于每个δ,δ ∈E(T′, f1) = {0, 1, 2},在树G中加入节点v0,v1,v2,分别与连接节点f1相连并将边标记为0,1,2,分别用子表T(f2, 0) (f1, 0)、T(f2, 0) (f1, 1)、T(f2, 0) (f1, 2)标记节点v0,v1,v2,结果如图3所示。重复上述过程得到最终的决策树(图4)。
为了和已有文献 [4] 中所采用的基于最大权值指标贪心选择策略的决策树分析过程进行比较,使用表10的数据采用最大权值贪心选择指标策略进行决策树构造,得到结果如图5所示。比较图4和图5中节点数量,我们可以知道,选择权值和作为不纯度函数可以缩小决策树的规模。
5. 总结
本文基于贪心算法思想,提出了一种非一致决策表的决策树分析方法。采用多值决策将非一致决策
Table 9. Greedy algorithm
表9. 决策树构造算法
Table 10. A many-valued decision table T
表10. 多值决策表T
Table 11. A many-valued decision table
表11. 多值决策表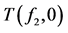
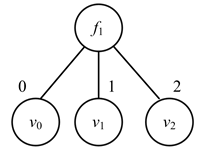
Figure 2. Decision tree for the first step
图2. 第一步贪心选择构造的决策树

Figure 3. Decision tree for the second step
图3. 第二步贪心选择构造的决策树
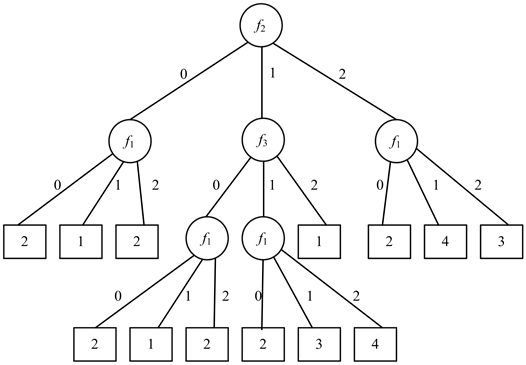
Figure 4. Decision tree building by the weighted sum and misclassification error
图4. 使用权值和贪心选择指标构造的最终决策树
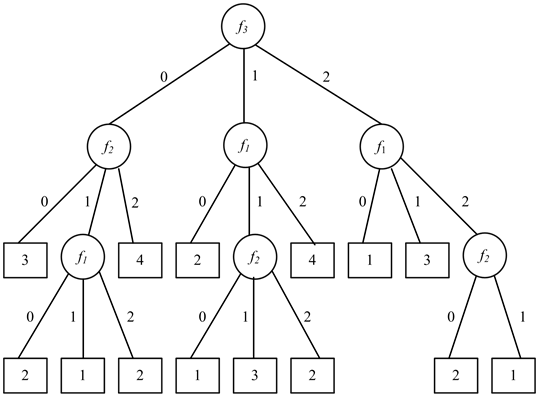
Figure 5. Decision tree building by the weighted max and misclassification error
图5. 使用最大权值贪心选择指标构造的最终决策树
表转换成多值决策表,使用不纯度函数和不确定指标设计决策树构造算法,实现决策树的构造。现实生活中经常会遇到非一致决策表的数据分类问题,例如,邮政局报刊征订部门根据以往客户订购报刊杂志类型的历史记录,预测客户可能订购的刊物类型,而刊物类型具有多个分类属性;具有多个语义标注的图像视频分类问题;以及基因组的功能分类等问题,通过该方法可以处理上述非一致决策表的数据分类问题。我们的下一步工作是寻找更好的贪心指标,并与动态规划算法进行比较,实现更好的决策树分析方法。
基金项目
国家自然科学基金面上项目(61572442, 61272130)浙江省科技厅公益性技术应用研究项目(
文章引用
许美玲,乔莹,曾静,莫毓昌,钟发荣. 非一致决策表的决策树分析
Decision Tree Analysis for Inconsistent Decision Tables[J]. 计算机科学与应用, 2016, 06(10): 597-606. http://dx.doi.org/10.12677/CSA.2016.610074
参考文献 (References)
- 1. Moshkov, M. and Zielosko, B. (2011) Combinatorial Machine Learning-A Rough Set Approach, ser. Studies in Computational Intel-ligence. Springer, Berlin, Vol. 360.
- 2. Tsoumakas, G. and Katakis, I. (2007) Multi-Label Classification: An Overview. International Journal of Data Warehousing and Mining (IJDWM), 3, 1-13. http://dx.doi.org/10.4018/jdwm.2007070101
- 3. Cour, T., Sapp, B., Jordan, C. and Taskar, B. (2009) Learning from Ambiguously Labeled Images. IEEE Conference on Computer Vision and Pattern Recognition, 20-25 June 2009, 919-926. http://dx.doi.org/10.1109/CVPRW.2009.5206667
- 4. Hüllermeier, E. and Beringer, J. (2006) Learning from Ambiguously Labeled Examples. Intelligent Data Analysis, 10, 419-439.
- 5. Jin, R. and Ghahramani, Z. (2002) Learning with Multiple Labels. Neural Information Processing Systems, Vancouver, 9 December 2002, 897-904.
- 6. Azad, M., Chikalov, I., Moshkov, M. and Zielosko, B. (2012) Greedy Algorithm for Construction of Decision Trees for Tables with Many-Valued Decisions. Proceedings of the 21st International Workshop on Concurrency, Specification and Programming, Berlin, 26-28 September 2012, CEUR-WS.org, Vol. 928.
- 7. Azad, M. and Moshkov, M. (2014) Minimization of Decision Tree Average Depth for Decision Tables with Many- Valued Decisions. Procedia Computer Science, 35, 368-377. http://dx.doi.org/10.1016/j.procs.2014.08.117
- 8. Dembczynski, K., Greco, S., Kotlowski, W. and Roman, S. (2007) Optimized Generalized Decision in Dominance- Based Rough Set Approach. 2nd International Conference on Rough Sets and Knowledge Technology, Toronto, 14-16 May 2007, 118-125.
- 9. Azad, M., Chikalov, I. and Moshkov, M. (2013) Three Approaches to Deal with Inconsistent Decision Tables— Comparison of Decision Tree Complexity. Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing, 46-54.
- 10. Mingers, J. (1988) An Empirical Comparison of Selection Measures for Decision-Tree Induction. Machine Learning, 3, 319-342. http://dx.doi.org/10.1007/BF00116837
- 11. Azad, M. and Moshkov, M. (2014) “Misclassification Error” Greedy Heuristic to Construct Decision Trees for Inconsistent Decision Tables. Proceedings of the International Conference on Knowledge Discovery and Information Retrieval, Rome, 184-191. http://dx.doi.org/10.5220/0005059201840191
