Modeling and Simulation
Vol.05 No.03(2016), Article ID:18309,8
pages
10.12677/MOS.2016.53011
Improved Split Bregman Method for Fluorescence Microscopic Image Restoration
Changchun Zhang, Yu Wang*, Hongbing Xiao
School of Computer and Information Engineering, Beijing Technology and Business University, Beijing

Received: Jul. 24th, 2016; accepted: Aug. 14th, 2016; published: Aug. 17th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Fluorescence microscopic image restoration has many very important applications such as astronomical imaging, electronic microscopy, single particle emission computed tomography (SPECT) and positron emission tomography (PET). Traditional total variation imaging restoration based on split Bregman algorithm can preserve sharp edges and save the image texture. Serious staircase effect phenomena, however, is generally accompanied. Therefore an improved image restoration algorithm is proposed based on split Bregman in this paper, which is mainly considered two aspects. One is that the total variation regularization model is used, which is an effective tool to recover blurred images. The other is that the weight function of the total variation is involved, which can not only suppress the staircase effect, but also preserve the image texture information. By appropriately choosing the reasonable parameters, the better restoration results can be obtained. The experimental results on synthetic images and real fluorescence microscopic images show the effectiveness and feasibility of the proposed algorithm.
Keywords:Split Bregman Algorithm, Weighted, Total Variation Regularization, Image Restoration

改进的分裂Bregman方法荧光显微图像复原
张长春,王瑜*,肖洪兵
北京工商大学计算机与信息工程学院,北京

收稿日期:2016年7月24日;录用日期:2016年8月14日;发布日期:2016年8月17日

摘 要
荧光显微图像复原有着很多重要的应用,例如,天文成像,电子显微镜成像,单光子发射计算机断层成像术和正电子发射断层成像技术等等。传统基于全变差的分裂Bregman算法能够很好地保护图像边缘和纹理信息,但在图像的平滑区域会产生严重的阶梯效应,针对这一问题,本文提出了一种复原算法,主要考虑两点,一是采用全变差(Total Variation, TV)正则化模型,可以很好地复原模糊图像。二是引入权函数,对TV进行加权抑制阶梯效应,同时保护了图像的纹理信息。通过对参数的合理选择,获得最佳的复原效果,在模拟图像和真实荧光显微图像的实验结果验证了该算法的有效性和可行性。
关键词 :分裂Bregman算法,加权,全变差正则化,图像复原

1. 引言
荧光显微镜方法是一种新兴有效的显微镜成像技术,在生物医学研究中,它能够提供活体样本的三维图像 [1] 。但是,由于成像系统衍射和噪声干扰等 [2] 因素,荧光显微图像不可避免出现模糊和噪声等退化现象,荧光显微图像的质量通常受两个因素影响:一是由显微光学成像系统的物理限制而导致的模糊,用点扩散函数 [3] (Point Spread Function PSF)来表征;二是测量工作大多在低光子流的情况下进行,因此会产生泊松噪声。面对这些固有的光学限制,以及对高质量图像的大量需求,用数字图像处理技术去除这些模糊和噪声是一项很有意义的工作。
目前,分裂Bregman算法 [4] - [7] 是求解范数最优化问题及其相关优化问题的最有效的方法之一,它是Rudin [8] 等学者提出的一种基于Bregman距离的迭代正则化算法 [9] - [11] ,起初是用于图像去噪,后来Goldstein [12] 在此基础上提出了分裂Bregman迭代图像复原模型。
Brette等人 [13] 提出了基于各项同性扩散的目标边缘保护先验知识,即全变差正则化 [11] 。全变差图像复原是基于变分的思想,把全变差图像复原模型转化为一个偏微分方程求解的过程。目前典型求解方法是根据Wang Yilun、Yang Junfeng等 [14] 提出的基于变量分离和半二次惩罚函数法的快速全变差反卷积算法 [15] (Fast Total Variation deconvolution, FTVd),把图像复原模型看作是一个无约束问题优化求解,实验结果验证了FTVd的有效性和稳定性。Setzer等 [16] 提出了分裂Bregman算法复原被泊松噪声污染的模糊图像,与其他的图像复原算法相比,它的优点在于不存在内部迭代及迭代过程中不产生负像素值。后来,王静等人 [7] 提出了基于分裂Bregman方法的全变差图像去模糊算法,首先利用辅助变量及其二次惩罚泛函把全变差去模糊优化问题转化成一个等价的无约束优化问题,然后基于Bregman迭代将其分解为两个子优化问题采用交替最小化方法 [15] 进行求解,接着根据子问题结构特点,采用离散傅里叶变换及收缩技术实现子优化问题的快速计算。
传统全变差分裂Bregman算法图像去模糊是假设图像在高斯噪声破坏情况下进行的,当图像实际被泊松噪声污染时,该算法虽然能在一定程度上抑制阶梯效应,但是复原效果并不理想,并且在噪声影响过大的情况下,去模糊效果会有所下降。针对图像被泊松噪声污染并且噪声影响过大去模糊效果不理想的情况,本文在传统基于分裂Bregman方法的全变差图像去模糊算法的基础上,引入TV约束模型和权函数,将加权TV约束模型与分裂Bregman方法有效地结合,既可以保留图像的边缘信息,又可以抑制平滑区域的阶梯效应,达到更好的去模糊效果。
2. 相关工作
图像复原就是根据一定的先验知识(如:模糊核),从已知的的模糊图像复原真实图像,其图像退化的模型如下:
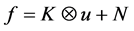 (1)
(1)
其中,f、u分别是模糊图像和真实图像,K是模糊核矩阵,N是加入的噪声,“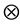 ”表示卷积运算。
”表示卷积运算。
2.1. 基本分裂Bregman算法
假设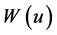 和
和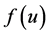 是关于变量u的凸能量泛函,则关于u的无约束化问题的形式是:
是关于变量u的凸能量泛函,则关于u的无约束化问题的形式是:
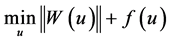 (2)
(2)
引入辅助变量d,则得到与公式(2)等价的约束优化问题的形式:
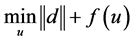 s.t.
s.t. (3)
(3)
根据变量分离理论,对式(3)加入Lagrange乘子 [16] ,便可到关于u和d的无约束优化问题:
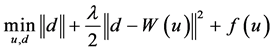 (4)
(4)
式中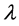 是惩罚系数,
是惩罚系数,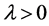 。基于分裂Bregman理论 [7] ,引入辅助变量
。基于分裂Bregman理论 [7] ,引入辅助变量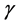 ,则得到关于u和d及
,则得到关于u和d及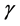 的迭代更新公式:
的迭代更新公式:
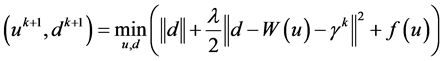 (5)
(5)
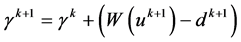 (6)
(6)
利用交替极小化的方法 [14] ,可分别得到变量u、d的更新公式:
 (7)
(7)
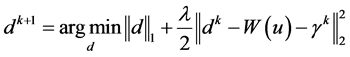 (8)
(8)
2.2. 算法收敛性
参考文献 [6] [9] 保证了算法的收敛性,其证明如下:
假设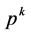 和
和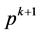 分别表示
分别表示 和
和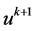 的梯度函数,
的梯度函数,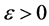 和
和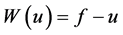 ,根据平均理论有:
,根据平均理论有:
 (9)
(9)
其中,D表示Bregman距离,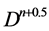 为对角矩阵,
为对角矩阵,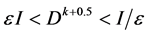 ,
,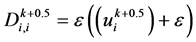 ,
, 是
是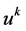 和
和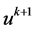 之间的值,故我们可以得到如下的公式:
之间的值,故我们可以得到如下的公式:
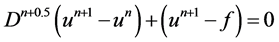 (10)
(10)
然后,对公式(10)两边同时乘以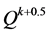 ,其中
,其中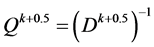 ,则公式(10)可以重新表示为:
,则公式(10)可以重新表示为:
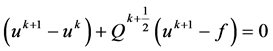 (11)
(11)
最后,对公式(11)两边同时减去f,我们可以得到公式(12):
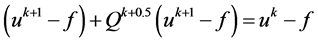

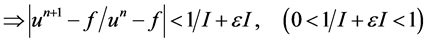 (12)
(12)
根据以上的讨论,我们可以得到分裂Bregman算法是收敛的。
3. 改进的图像复原算法
传统全变差分裂Bregman算法是假设图像在高斯噪声破坏的情况下进行的,当实际图像被泊松噪声破坏时,该算法虽能在一定程度上抑制阶梯效应,但当存在很大的泊松噪声时,复原效果并不理想,针对这种情况,本文提出一种新算法,即引入加权的全变差约束模型,来抑制阶梯效应,同时也保存了图像的纹理,得到了很好的复原效果。
3.1. 算法改进
在本文中,提出了引入加权全变差约束模型,根据变量分离理论和分裂Bregman算法,进行荧光显微图像复原。则公式(1)的目标函数如下:
 (13)
(13)
其中, ,
,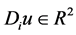 表示u在像素i水平方向和垂直方向的一阶有限差分,
表示u在像素i水平方向和垂直方向的一阶有限差分,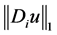 表示变量u在像素i处的变差数,
表示变量u在像素i处的变差数,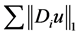 表示对所有的i
表示对所有的i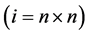 求和,
求和,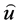 设置为u,
设置为u,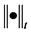 表示t–范数,第二项
表示t–范数,第二项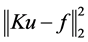 是保真项,
是保真项,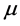 是正则化参数,
是正则化参数,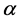 表示权函数,其表达式是公式(14)所示:
表示权函数,其表达式是公式(14)所示:
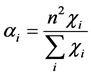 ,
,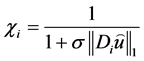 (14)
(14)
全变差图像去模糊的问题可以看作是一个无约束问题优化问题。因此,引入辅助变量y,式(13)可以转化为关于u和y的无约束模型:
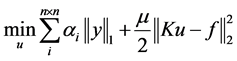 s.t.
s.t.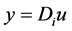 (15)
(15)
添加变量u和y的二次惩罚项,转化为与式(15)等价的关于u和y的最优化问题的模型:
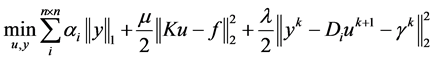 (16)
(16)
基于变量可分离理论和分裂Bregman迭代,可以转化为求关于u和y两个子优化问题,于是,得到关于变量u和y以及参数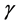 的迭代更新迭代公式:
的迭代更新迭代公式:
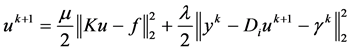 (17)
(17)
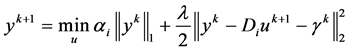 (18)
(18)
 (19)
(19)
本文图像复原算法图像边界条件设为周期型边界,K和D均是块循环矩阵。在求解子问题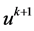 时,对式(17)中的
时,对式(17)中的 求导并且令导数为零,可得到如下形式:
求导并且令导数为零,可得到如下形式:
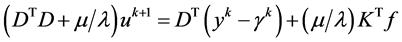 (20)
(20)
采用FFT及其反变换得到与(17)式等价形式的快速求解u的迭代公式:
 (21)
(21)
式中“*”表示复共轭,“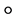 ”表示分量分式乘积,F、F−1分别表示傅里叶变换及其逆变换。
”表示分量分式乘积,F、F−1分别表示傅里叶变换及其逆变换。
求解子问题y,根据式(18)的结构特点,可利用shrink函数求解,其定义如下:
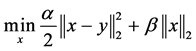 (22)
(22)
其解的形式为:
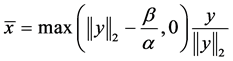 (23)
(23)
其中规定 。
。
由式(22)和(23),可得到子问题y的快速更新迭代公式为:
 (24)
(24)
3.2. 算法流程
本文算法是假设PSF已知,故可以由快速迭代式(21)得到目标图像 ,然后根据式(24)和(19)更新得到的数值带入到式(21),最后得到更新后的图像
,然后根据式(24)和(19)更新得到的数值带入到式(21),最后得到更新后的图像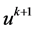 ,收敛精度tol取经验值
,收敛精度tol取经验值 。表1给出了本文算法的具体流程。
。表1给出了本文算法的具体流程。
4. 评价准则
图像复原的质量评价包括主观评价和客观评价,而主观评价包含了人的视觉特性和心理因素,其评价结果较符合实际观察到的图像质量,但有一定的随意波动性,在实际应用中因过程繁琐并且无法完全重复受到了严重的限制。本文中采用信噪比 [14] (Signal to Noise Ratio, SNR)作为客观的图像复原质量的标准:
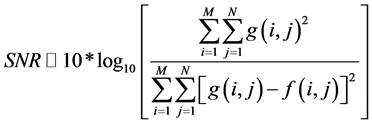 (25)
(25)
式中M和N分别表示图像长度和宽度上的像素个数,g(i,j)和f(i,j)分别是原始图像和复原图像在点(i,j)处的灰度值,信噪比的数值越大,图像质量越好。
5. 仿真结果与分析
为了验证本文算法的有效性,分别使用人工合成的模糊噪声图像和真实的荧光显微图像进行了验证,并且同FTVd-FM算法 [15] ,传统分裂Bregman算法 [7] 进行了比较,实验编译环境为Matlab,个人PC机:Inter Core双核,3.60 GHz,4 GB内存。使用SNR作为客观评价方法评价图像复原的质量。
5.1. 合成图像
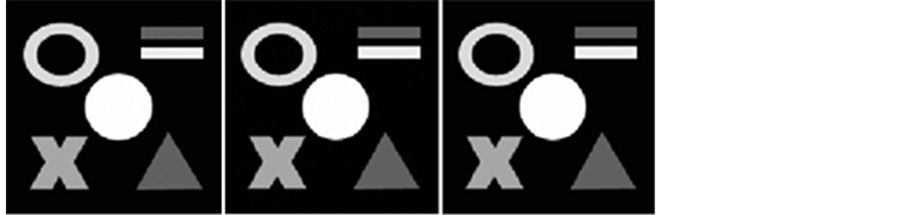
在合成的模糊噪声图像上应用本文算法,图1(a)为合成图像(130 × 130像素),图1(b)是其对应的退化图像(泊松噪声和模糊)。在我们的实验中采用高斯PSF(大小5 × 5,标准差为1.5),复原结果如图2所示。
从图2可以看出,FTVd-FM算法存在明显的阶梯效应;传统分裂Bregman算法虽然一定程度上减轻了阶梯效应,但得到的图像边缘仍存在部分阶梯效应;本文算法得到的复原图像阶梯效应得到明显改善。
5.2. 真实图像
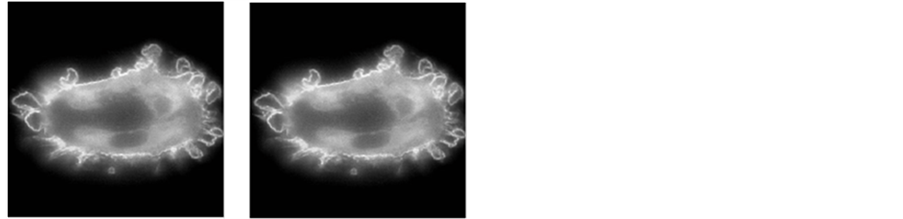
为了验证算法的有效性和实用性,本文采用了真实的荧光显微图像进行了相关实验。图3(a)是真实观察到的荧光显微图像(512 × 512像素),由于并未知该图像的具体参数信息,因此,实验时仍然采用人工人工合成图像中的PSF值。
利用人工合成图像实验所得到的相关参数在真实荧光显微图像上进行实验。图3(b)是采用FTVd-FM算法得到的复原图像。从图中可以看出,复原的图像在明显的阶梯效应;图3(c)是使用传统分裂Bregman算法,从图中可以看出,阶梯效应得到了明显的抑制,但是仍然存在部分阶梯效应,影响复原图像的质量。图3(d)是利用本文算法得到的复原图像,从图中可以看出,使用本文算法既有效的抑制了阶梯效应,又保持了图像在平滑区域的光滑性和图像边缘区域的细节信息。
为了更加直观的观察复原结果的细节信息,我们对图3(a)中的黑色矩形框标记的区域进行了放大,图4(a),图4(b),图4(c)和图4(d)是分别对应图3(a),图3(b),图3(c)和图3(d)中相对应的区域。
Table 1. The flow of the improved split Bregman image restoration method
表1. 改进的分裂Bregman图像复原算法流程
 (a) (b)
(a) (b)
Figure 1. Synthetic image (a) original image, (b) degraded image
图1. 合成实验图像(a)原图,(b)退化图像
 (a) (b) (c)
(a) (b) (c)
Figure 2. Restored images by (a)FTVd-FM method (SNR = 45.50 dB), (b) traditional split Bregman method (SNR = 45.50 dB), (c) our method (SNR = 49.68 dB)
图2. 图像复原结果(a) FTVd-FM算法(SNR = 45.50 dB),(b) 传统分裂Bregman算法(SNR = 45.50 dB),(c) 本文算法(SNR = 49.68 dB)

 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 3. (a) The degradation of the image, the restored image by the (b) FTVd-FM method, (c) traditional split Bregman method, and (d) our method
图3. 真实荧光显微图像图像复原结果;(a) 退化图像,(b) FTVd-FM算法,(c) 传统分裂Bregman算法,(d) 本文算法
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 4. A close-up of (a) Figure 3 (a), the corresponding close-up of (b) Figure 3 (b), (c) Figure 3 (c) and (d) Figure 3 (d)
图4. (a)图3(a)的局部放大图,(b)图3(b)的局部放大图,(c)图3(c)的局部放大图,(d)图3(d)的局部放大图
6. 结束语
本文在分裂Bregman算法的基础上提出了一种新的图像复原算法,引入了权函数,通过对TV加权,抑制阶梯效应,提高图像复原效果,同时可以很好地保护图像的纹理信息。通过对参数的合理选择,获得了较好的复原效果。在合成图像和真实的荧光显微图像上的实验结果验证了算法的有效性和可行性,但是需要特别强调的是,在图像的模糊核过大的情况下,本文算法的图像复原效果会有所下降,这将是下一步研究工作中的主要任务。
基金项目
北京市自然基金面上项目(No. 4162018);北京市委组织部青年拔尖人才支持计划项目(No. 20140000 26833ZK14);北京市属高等学校高层次人才引进与培养计划项目(No.CIT&TCD201504010)。
文章引用
张长春,王瑜,肖洪兵. 改进的分裂Bregman方法荧光显微图像复原
Improved Split Bregman Method for Fluorescence Microscopic Image Restoration[J]. 建模与仿真, 2016, 05(03): 81-88. http://dx.doi.org/10.12677/MOS.2016.53011
参考文献 (References)
- 1. Lefkimmiatis, S., Bourquard, A. and Unser, M. (2012) Hessian-Based Regularization for 3D Microscopy Image Restoration. 9th IEEE International Symposium on Biomedical Imaging, Barcelona, 2-5 May 2012, 1731-1734.
- 2. Chaux, C., Blanc-Féraud, L. and Zerubia, J. (2007) Wavelet-Based Restoration Methods: Application to 3D Confocal Microscopy. SPIE Proceedings, 6701, 78-89. http://dx.doi.org/10.1117/12.731438
- 3. Zhang, B., Fadili, J., Starck, J.-L. and Olivo-Marin, J.-C. (2007) Multiscale Va-riance-Stabilizing Transform for Mixed Poisson Gaussian Processes and Its Applications in Bio-Imaging. IEEE International Confe-rence on Image Processing, Vol. 6, San Antonio, 16 September-19 October 2007, 233-236.
- 4. Getreuer, P. (2012) Total Variation Deconvolution Using Split Bregman. Image Processing on Line, 2, 158-174. http://dx.doi.org/10.5201/ipol.2012.g-tvdc
- 5. Goldstein, T. and Osher, S. (2009) The Split Bregman Algorithm for L1 Regu-larized Problems. SIAM Journal on Imaging Sciences, 2, 323-343. http://dx.doi.org/10.1137/080725891
- 6. Li, Y.F. and Feng, X.C. (2010) The Split Bregman Method for L1 Projection Problems. Acta Electronica Sinica, 38, 2471-2475.
- 7. Wang, J., Lü, K., He, N. and Wang, Q. (2012) Total Variant Image Deblurring Based on Split Bregman Method. Acta Electronica Sinica, 40, 1503-1508.
- 8. Rudin, L., Osher, S. and Fatemi, E. (1992) Nonliner Total Variation Based Noise Removal Algorithm. Physica D, 60, 259-268. http://dx.doi.org/10.1016/0167-2789(92)90242-F
- 9. Osher, S., Burger, M., Goldfarb, D., Xu, J.J. and Wotao, Y. (2005) An Iterative Regularization Method for Total Variation-Based Image Restoration. Multiscale Modeling and Simulation, 4, 460-489. http://dx.doi.org/10.1137/040605412
- 10. Tikhonov, A.N. and Arsenin, V.Y. (1997) Solutions of Ill-Posed Problems. V.H. Winston & Sons, Washington DC.
- 11. Babacan, S., Moluna, R. and Katsaggelos, A. (2008) Parameter Estimation in TV Image Restoration Using Variational Distribution Approximation. IEEE Transactions on Image Processing, 17, 326-339. http://dx.doi.org/10.1109/TIP.2007.916051
- 12. Goldstein, T. and Osher, S. (2009) The Split Bregman Algorithm for L1 Re-gularized Problems. SIAM Journal on Imaging Sciences, 2, 323-343. http://dx.doi.org/10.1137/080725891
- 13. Brette, S. and Dier, J. (2006) Optimized Single Site Update Algorithms for Image Deblurring. International Conference on Image Processing, Vol. 3, Lausanne, 16-19 September 1996, 65-68. http://dx.doi.org/10.1109/ICIP.1996.560370
- 14. Yin, W.T. and Yang, J.F. (2009) Alternating Direction Algorithms for Total Variation Deconvolution in Image Reconstruction. http://www.optimization-online.org/DB-HTML/2009/11/2463.html
- 15. Yang, J.F., Yin, W.T., Zhang, Y. and Wang, Y.L. (2009) A Fast Algorithm for Edge-Preserving Variational Multichannel Image Restoration. SIAM Journal on Imaging Sciences, 2, 569-592. http://dx.doi.org/10.1137/080730421
- 16. Setzer, S., Steidl, G. and Teuber, T. (2010) Deblurring Poissonian Images by Split Bregman Techniques. Journal of Visual Communication and Image Representation, 21, 193-199. http://dx.doi.org/10.1016/j.jvcir.2009.10.006
