Modeling and Simulation
Vol.
12
No.
03
(
2023
), Article ID:
64967
,
14
pages
10.12677/MOS.2023.123161
三维Y肋相变蓄热器的热性能数值模拟及分析
叶文兰,赵明,姚莉,方强
上海理工大学能源与动力工程学院,上海
收稿日期:2023年2月19日;录用日期:2023年4月29日;发布日期:2023年5月6日

摘要
运用数值模拟的方法,研究了三维Y型肋片不同分布时模型对相变蓄热器蓄放热过程以及入口流速对蓄热过程的影响。结果表明:首先,在轴向不同位置处,蓄放热过程有明显差异,特别是蓄热过程;其次,Y型肋片越向底部聚集,自然对流持续时间越长,蓄热效果越好;在蓄热过程中,模型5 (30˚ Y型肋片模型)相比于模型2 (72˚ Y型肋片模型)蓄热时间缩短了19.01%,在放热过程中,模型2、模型3、模型4和模型5相比于模型1放热时间分别缩短了67.77%、44.39%、22.65%和12.20%。最后,提高换热流体入口流速可明显缩短熔化时间,但对蓄热速率的增大程度有一定范围。当入口速度大于0.1 m/s时,入口速度对熔化时间的影响显著降低。
关键词
三维相变蓄热器,Y肋模型,数值模拟,流速,自然对流

Numerical Simulation and Analysis of Thermal Performance of a Three-Dimensional Y-Ribbed Phase Change Heat Accumulator
Wenlan Ye, Ming Zhao, Li Yao, Qiang Fang
School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai
Received: Feb. 19th, 2023; accepted: Apr. 29th, 2023; published: May 6th, 2023

ABSTRACT
Using the method of numerical simulation, the effects of the model with different distribution of three-dimensional Y-shaped fins on the heat storage and release process of phase change heat storage unit and the inlet velocity on the heat storage process were studied. The results show that: firstly, there are obvious differences in the heat storage and release process at different axial positions, especially in the heat storage process; Secondly, the more Y-shaped fins gather to the bottom, the longer the duration of natural convection, and the better the heat storage effect; In the heat storage process, the heat storage time of model 5 (30˚ Y-rib model) is shortened by 19.01% compared with model 2 (72˚ Y-rib model), and in the heat release process, the heat release time of model 2, model 3, model 4 and model 5 is shortened by 67.77%, 44.39%, 22.65% and 12.20% respectively compared with model 1. Finally, increasing the inlet flow rate of heat exchange fluid can significantly shorten the melting time, but it has a certain range for the increase of heat storage rate. When the inlet velocity is greater than 0.1 m/s, the effect of inlet velocity on melting time decreases significantly.
Keywords:Three Dimensional Phase Change Heat Storage Unit, Y-Rib Model, Numerical Simulation, Current Speed, Natural Convection

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
储热技术被认为是解决太阳能、风能、地热能等可再生能源连续性问题的关键。储热分为化学储热、显热储热和相变储热,其中相变储热与显热储热相比,储热密度更大、结构更紧凑,且相变过程相变温度变化稳定,与化学储热相比更安全、更易控制,相变储热已成为国内外研究热点。
为强化相变蓄放热性能,在相变蓄热器结构中添加翅片是主要手段。Zhang [1] 等人通过数值模拟的方法研究了四种不同翅片布置(下翅片、上翅片、中翅片和算术翅片)的LHTE热性能,结果表明,采用算术翅片可使完全熔化时间缩短49.9%,使性能最大化,且相变材料在熔化过程均匀性最大。Yu、M. Alizade [2] [3] [4] 等人通过仿生学的方法建立了树状、V形和Y形肋片,运用响应面法对肋片进行优化,分别获得了最优的肋片几何参数,数值模拟结果表明在潜热储能系统中多级肋片可加快相变过程以及使温度场更均匀。张峰鸣 [5] 采用数值模拟的方法对4种多相变材料的分腔式蓄热模型的蓄热过程进行了分析,结果表明对于不同的分腔模型采用不同PCM组合填充方案能获得更好的蓄热效果。任智彬 [6] 等人通过数值模拟的方法对三维不同肋片模型的相变蓄热单元的蓄放热特性进行了分析,结果表明,添加分形肋片可以大大提高相变蓄热单元的蓄放热速率,并且Y型肋片相比于T型肋片整体效果要好。林道光 [7] 等人以内翅式套管相变蓄热器为研究对象,运用数值模拟的方法探讨了蓄热器内翅片个数、翅片高度、翅片厚度等因素对石蜡蓄热过程的影响,结果表明自然对流在内翅式套管相变蓄热器蓄热过程中有重要作用,且翅片个数、高度和厚度的增加均能加强换热,但增强换热效率会趋于平缓。
综上所述,国内外学者在蓄热器结构优化方面做了大量的工作,但大多文献较少从三维上对模型进行研究和较少涉及到关注蓄热器底部PCM难熔问题并且在这一方面上结合自然对流作用的影响进行研究。本文建立了三维相变蓄热器模型,考虑自然对流的作用,并考虑流体侧对流换热、壁面导热和相变区的耦合换热,通过数值模拟方法研究Y型肋片不同分布以及不同入口速度对相变蓄热单元蓄放热的影响,同时分析轴向和径向上传热差异特性,为蓄热器的结构优化提供参考。
2. 问题描述和数值模型
2.1. 物理模型
所建立的物理模型如图1所示,共有5种不同结构的蓄热器模型,分别是:模型1 (光管模型)为文献 [8] 所用模型,该模型用来对比和验证数值模拟的结果,并和Y型肋片模型相比较;模型2为72˚ Y型肋片模型(肋片均匀分布);模型3为60˚ Y型肋片模型,模型4为45˚ Y型肋片模型,模型5为30˚ Y型肋片模型。Y型肋片厚度为0.001 m,整体高度为0.032 m。所有模型肋片填充量均相同,与内管之间以拼接的方式进行连接,流动方向为x轴正方向。所有模型内管内径为0.038 m,外径为0.040 m,外管外径为0.12 m,管长为1 m。内管外管和肋片材料均为铜,内管管内流动介质为水,内外管之间填充的相变材料为RT50,其热物性参数如表1所示。
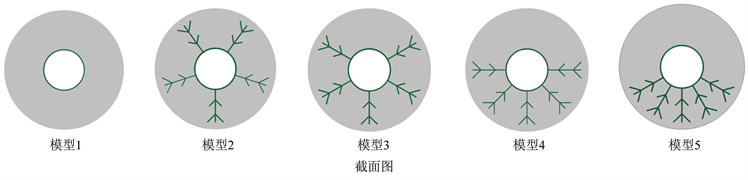
Figure 1. Physical model diagram
图1. 物理模型简图
2.2. 数学模型及边界条件
2.2.1. 数学模型
为方便分析,对模型作以下几点假设:
1) 综合考虑计算精度和计算时间,传热流体采用一维分布参数模型,传热流体轴向导热和粘性耗散忽略不计;
2) 相变材料热物性取常数;
3) 相变蓄热单元内管壁热阻忽略不计,外管表面当绝热处理;
4) 相变材料的密度符合Boussinesq假设。
Table 1. Physical parameters of phase change materials
表1. 相变材料物性参数表
2.2.2. 控制方程
引入焓法模型 [9] 对相变过程中的边界移动问题进行处理。依据上述假设,传热流体测采用一维分布参数法模型,控制方程如:
(1)
相变材料侧为了考虑自然对流的影响,采用三维柱坐标模型,动量方程如下:
(2)
(3)
(4)
能量方程为:
(5)
式中: 为换热流体温度、 为换热流体质量流量、 为换热流体密度、 为内管外径、h为对流换热系数、 为相变材料温度、 为动力粘度、 为膨胀系数、 为传热流体给定入口温度、L为相变材料潜热、λ为相变材料导热系数、 为箱变材料比热、f为相变材料液化分数。
2.2.3. 初始条件及边界条件
初始条件:蓄热过程初始时刻相变材料及传热流体的温度为298.15 K,边界条件设置如下。
1) 传热流体侧 采用给定入口温度和流速的第一类边界条件。在蓄热过程中,入口温度为353.15 K,入口流速分别为0.02 m/s,0.1 m/s、0.5 m/s,1 m/s。在放热过程中,入口温度为298.15 K,入口流速为0.2 m/s。
2) 相变材料侧 外壁面采用绝缘边界,PCM和肋片交界面采用coupled耦合边界条件。
2.3. 数值计算及模型考核
采用ANSYS FLUENT软件进行数值模拟计算,引入基于焓值方法的Solidification & Melting模型对相变过程进行模拟,物性参数和温度的关系采用UDF实现。
模型整体上进行结构化划分。对比分析模型整体网格数分别为480,113、750,351、1,000,839和1,800,257时PCM液相分数以及平均温度的变化情况。网格考核结果如图2所示。
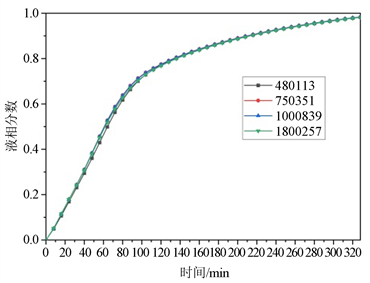 (a) 不同网格数的液相分数
(a) 不同网格数的液相分数
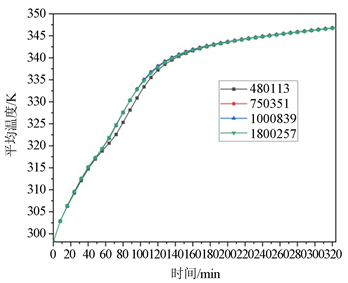 (b) 不同网格数的PCM平均温度
(b) 不同网格数的PCM平均温度
Figure 2. Grid independence verification
图2. 网格无关性验证
由图2(a)和图2(b)可知,在蓄热过程中,随着网格数目的增加,液相分数以及平均温度相差很小,最大计算误差分别为5.54%和0.71%。为考虑计算经济性,故选择网格数目为1,000,839。
在网格数目1,000,839情况下,对比分析模型时间步长分别为0.1 s、0.2 s、0.4 s时液相分数以及PCM平均温度的变化情况。经过考核,最大误差分别为0.52%和0.042%。故从计算经济性考虑出发,选择0.2 s作为后续计算的时间步长。时间步长考核结果如图3所示。
 (a) 不同时间步长的液相分数
(a) 不同时间步长的液相分数
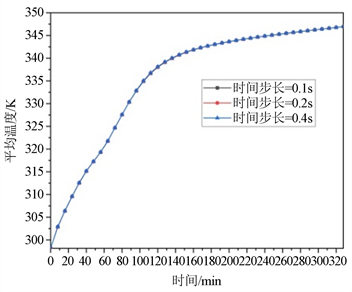 (b) 不同时间步长的PCM平均温度
(b) 不同时间步长的PCM平均温度
Figure 3. Time step verification
图3. 时间步长验证
如图4所示,通过将模型1的数值模拟结果与文献 [8] 所提供的实验数据进行对比,发现模拟结果T与文献实验数据最大误差为4.1%,数据吻合较好,因此模型验证正确。

Figure 4. Model validation verification
图4. 模型有效性验证
3. 结果与讨论
3.1. 不同肋片分布下三维蓄热单元的蓄热特性
首先,模拟了流体入口温度为353.15 K时模型1到模型5的蓄热过程。图6和图7为5个模型在t = 10 min、t = 30 min和t = 80 min时沿轴向上不同位置处截面的液相云图(图5左半部分)、温度云图(图5右半部分)和流场图(图6)。由图可知,蓄热过程可分为三个阶段。
阶段1:由液相图和温度图(图5(a))及流场图(图6(a))知,在熔化第一阶段以导热为主,此时所有模型内管外壁面及肋片附近产生液态薄层,液态薄层温度较高,流速较快。沿着流动方向,熔化的PCM逐渐减少。从模型2到模型5,当肋片逐渐向底部聚集时,有更多PCM在底部熔化,底部温度也较高,顶部还未受影响。
在不同轴向位置处,可以看到熔化情况有明显的差异。在x = 0.35 m及往后截面处,模型2到模型5的流场没有明显差异。此时,在x = 0.05 m截面处,模型1相比于其他模型,其流速稍微更大一点。对于各个模型内管的换热流体,可以看到沿着流动方向,有明显的温度分层现象,且低温区在逐渐增多。
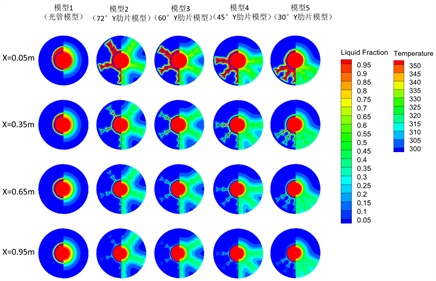 (a) 10 min
(a) 10 min
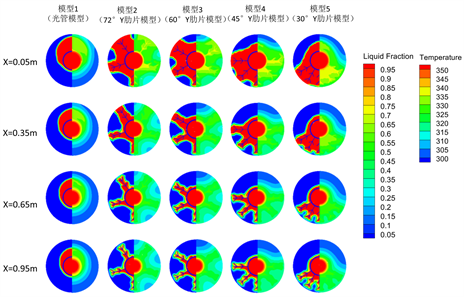 (b) 30 min
(b) 30 min
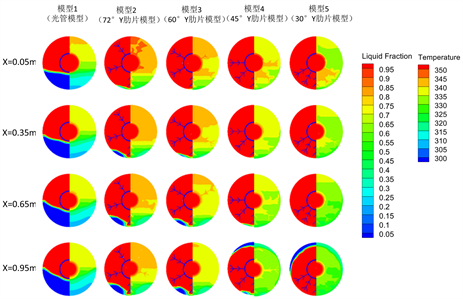 (c) 80 min
(c) 80 min
Figure 5. Liquid phase diagram (left) and temperature diagram (right) of heat storage process
图5. 蓄热过程液相图(左)和温度图(右)
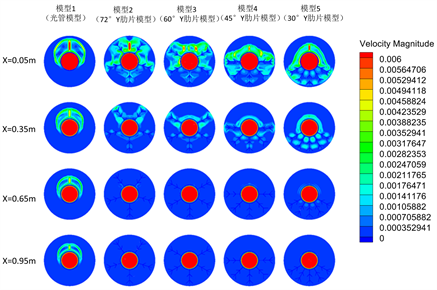
阶段2:在t = 30 min时,蓄热过程为综合作用阶段,导热和自然对流同时起作用,自然对流逐步增强。由液相图(图5(b))和流场图(图6(b))知,模型1已表现出明显的固液分层现象,且在重力和浮升力的影响下,熔化的液相PCM上移,使得固相PCM在蓄热器底部形成堆积。对于加肋的模型2到模型5,随着肋片逐渐向底部聚集,在蓄热器底部熔化的PCM逐渐增多;和10 min时相比,各模型形成自然对流的区域明显增多,且都更加强烈。
在不同轴向位置处,各模型熔化过程表现出不同的效果,且差异较大,沿着流动方向熔化PCM明显减少。由温度图和流场图可知,随着肋片逐渐向底部聚集,模型2到模型5的顶部区域温度均较低,出口处蓄热过程还以导热为主向自然对流为主转变,但入口处,蓄热过程早已以自然对流为主。模型5在入口处底部PCM已基本全部熔化,这增强了自然对流对上部区域的影响,但在管子尾端,肋片及内管壁附近生成的还是液态薄层,管子前后端熔化情况有很大差异,出口端熔化明显滞后于入口端。因此,管子前后端相比,熔化时间相差很大。在x = 0.05 m和x = 0.35 m截面处,可看到较明显的自然对流,但在x = 0.65 m以及x = 0.95 m截面处,模型2到模型5蓄热以导热向自然对流转变为主,但模型1可看到明显的自然对流,这是因为沿着流动方向热流体在模型1中相比于其他加肋模型换热量较少,热流体温度降低不大,管子后端换热依然很强。
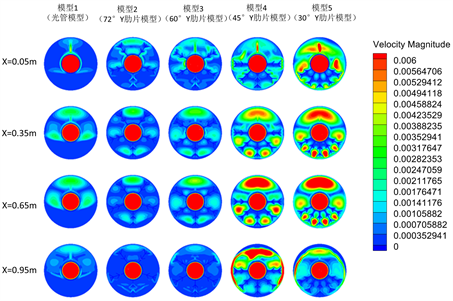
阶段3:在蓄热过程进行到80 min时,为蓄热过程完成阶段。由液相图(图5(c))可知,模型1上部的PCM已全部熔化,但在底部形成严重的固相PCM堆积;模型2到模型5的PCM整体已大部分熔化。模型2和模型3,由于上部有两个翅片,最后未熔化处于蓄热器底部;而模型4和模型5,由于肋片都集中在蓄热器底部,上部未熔PCM多于下部。对于各个模型的难熔区,模型1占到36.38%,而有肋模型,模型2占7.38%,模型3占3.43%,模型4只有极小一部分,而模型5不形成难熔区。难熔区的固相PCM熔化以导热为主,速度缓慢,而模型4和模型5上部固相PCM熔化以自然对流为主,可大大加快熔化。
在不同轴向位置处,模型5前三个不同截面位置PCM已全部熔化,但在x = 0.95 m处,有未熔PCM在蓄热器上方。由温度图(图5(c))和流场图(图6(c))可知,80 min时各模型不同轴向位置处熔化的PCM区域均有明显的流动,且与30 min时相比,流动更加强烈,这主要是因为随着肋片在底部聚集,下方的PCM温度高于上方的PCM温度,使得上下液相PCM交换,蓄热器整体温度分布更均匀。对于模型4和模型5,轴向位置从x = 0.05 m到x = 0.65 m,液相PCM流动更加强烈,而x = 0.95 m处流动比x = 0.65 m小,主要是因为管子前部分PCM最先全部熔化,尾端PCM较后熔化,且在出口处蓄热器上方还有未熔PCM,使得流动范围较小,流动较弱。
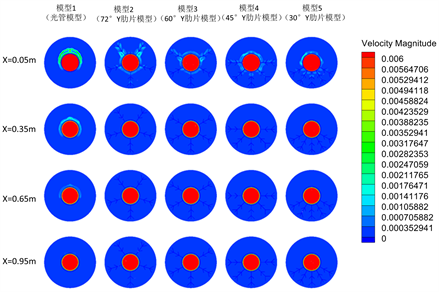 (a) 10 min
(a) 10 min
 (b) 30 min
(b) 30 min
 (c) 80 min
(c) 80 min
Figure 6. Flow field diagram
图6. 流场图
从图7液相分数图可以看出Y肋模型相比光管模型可大大缩短蓄热时间;对于Y肋模型,随着Y肋逐渐向底部聚集,可以明显加快熔化,缩短蓄热时间。其中模型3、模型4和模型5比Y肋均匀分布的模型2蓄热时间分别缩短了5.24%,13.28%,19.01%。
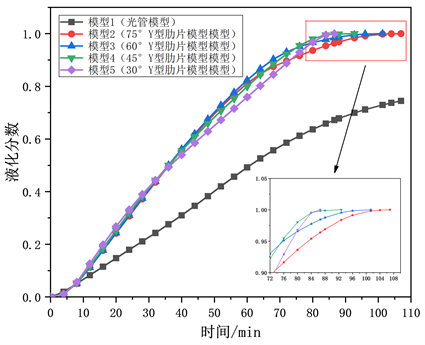
Figure 7. Change of liquid phase fraction during heat storage
图7. 蓄热过程液相分数的变化
3.2. 换热机理的演化
为了分析蓄热器蓄热过程的换热机理,引入平均 数 [10] ,定义如下:
(6)
式中 为PCM流体的平均对流换热系数,定义如下:
(7)
式中q为热流密度, 为壁面温度, 为液态临界温度。
图8展示了平均Nu数随时间的变化,根据曲线所展示的特征,蓄热器蓄热过程可以分为四个阶段。
阶段1,导热作用占主导地位。首先刚开始流入的流体加热管壁和肋片,管壁和肋片温度快速升高,此时被加热的相变材料平均Nu数也急剧增大。
阶段2,自然对流占主导地位。随着熔化过程的进行,液态薄层逐渐增厚,导热热阻增加,因此平均Nu数先减小。随着高温流体逐渐增多,自然对流作用逐渐增强,此时导热热阻变得很大,但二者相互影响之下平均Nu数有所回升。从液相图可知,不同轴向位置熔化情况差异很大,整体综合之下,导致平均Nu数回升程度并不大。
阶段3,自然对流逐渐向导热转变。随着蓄热过程的进行,热流体逐渐增多,固态PCM逐渐减少,产生自然对流的动力逐渐减弱,但减弱幅度并不大,主要原因是肋片更向底部聚集的模型底部液相流体比上部多,自然对流作用依然较强,可以维持更长时间,因此平均Nu数下降幅度较小。
阶段4,导热作用占主导地位。随着蓄热过程的进行,这个阶段PCM已大部分熔化,蓄热器热流体温度较趋于一致,自然对流效应很快变得微弱,换热主要以导热形式进行,因此平均Nu数以更快速度下降。由图可知,模型5向导热作用转变的拐点出现在更后面,其自然作用影响时间更长。

Figure 8. Change of average Nu number during heat storage
图8. 蓄热过程平均Nu数的变化
3.3. 不同入口速度对蓄热过程的影响
图9展示了4个不同Y型肋片分布模型在蓄热过程中热流体不同入口速度对熔化时间的影响。可以发现,入口速度对完全熔化时间有显著的影响。比如模型5,入口速度为0.1 m/s、0.5 m/s和1 m/s时,相比于0.02 m/s,完全熔化时间分别缩短了30.82%、46.36%和50.17%。主要原因是随着内管热流体流速的增大,到出口位置温度降低逐渐减小,使出口段热流体与PCM维持较大温差,加快熔化,缩短熔化时间。在入口速度为0.5 m/s以及1 m/s时,可以发现模型4比模型5的熔化时间短。另外,完全熔化时间可以直接描述融化速率 [8] ,随着入口速度的增大,熔化速率增大程度减小。当入口速度大于0.1 m/s时,入口速度对熔化时间的影响显著减少。
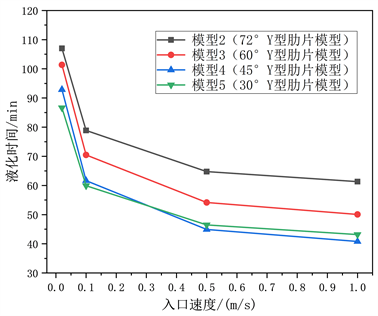
Figure 9. Effect of different inlet velocities on melting process
图9. 不同入口速度对熔化过程的影响
3.4. 放热过程模拟及结果分析
根据前面的方法,模拟了三维相变蓄热单元模型1到模型5的放热过程,如图10所示。从图中可知,不同模型的放热过程可分为三个阶段。阶段1:如图10(a),由于导热作用,内管壁面和肋片附近的液态PCM先凝固,此区域温度较低。沿着流动方向,内管壁面处的换热流体温度逐渐升高,此时换热流体与PCM的温差也较低,因此凝固范围减少。
 (a) 27 min
(a) 27 min
 (b) 67 min
(b) 67 min
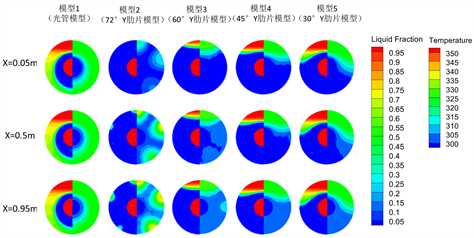 (c) 200 min
(c) 200 min
Figure 10. Liquid phase diagram (left) and temperature diagram (right) of exothermic process
图10. 放热过程液相图(左)和温度图(右)
阶段2:如图10(b),随着放热的进行,凝固的PCM逐渐增多,加肋模型凝固速度明显快于光管模型;当肋片逐渐向底部聚集时,底部凝固的PCM越多。模型5在入口处已将肋片夹角下的PCM全部凝固,且各模型从入口到出口处的各截面凝固的PCM逐渐减少,这是由于换热流体从入口开始被逐渐加热,沿着流向与PCM温差逐渐减小,从温度图中可以明显看出靠近壁面换热流体温度逐渐升高。
阶段3:如图10(c),模型2由于肋片分布更均匀,入口处的PCM已全部被凝固,模型2到模型5,由于肋片逐渐聚集在底部,导致顶部未凝固的PCM逐渐增多,且肋片间角度更大的模型温度分布更均匀。光管模型的凝固速度明显慢于有肋片模型。由于凝固主要依靠导热,可以看到轴向不同位置处凝固速度差异并不是很大。
由图11知,添加Y型肋片可以明显缩短放热时间,与模型1相比,模型2、模型3、模型4和模型5放热时间分别缩短了67.77%、44.39%、22.65%和12.20%。由图12可知,各模型的平均Nu数大部分时间都维持在比较低值,可以看出凝固过程主要以导热为主,由于模型2肋片分布更加均匀,形成更均匀的腔室,依靠Y型肋片的导热作用可以更快使PCM凝固,大大缩短凝固时间。
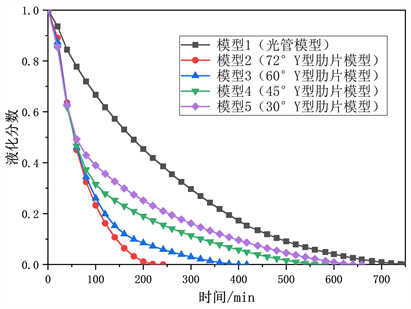
Figure 11. Change of liquid phase fraction during exothermic process
图11. 放热过程液相分数的变化

Figure 12. Variation of average Nu number during exothermic process
图12. 放热过程平均Nu数的变化
4. 结论
本文通过数值模拟的方法分别研究了Y型肋片不同分布情况对三维相变蓄放热过程以及入口流速对蓄热过程的影响,结论如下:
1) 三维相变蓄热器在轴向传热特性方面存在显著差异,尤其是蓄热过程;越靠近出口PCM熔化/凝固越滞后于入口部分。在蓄热过程,随着Y型肋片逐渐向底部聚集,径向自然对流作用持续时间更长,加快PCM熔化。
2) 添加Y型肋片的模型相比于光管模型可以明显缩短蓄热器的蓄/放热时间。对于Y型肋片不同分布情况的模型,在蓄热过程,模型5蓄热效果最好,相比于模型2蓄热时间缩短了19.01%;在放热过程,模型2放热效果最好,相比于模型1放热时间缩短了67.77%。
3) 换热流体入口流速的提高可明显缩短熔化时间,但对蓄热速率的增大程度有一定范围。当入口速度大于0.1 m/s时,入口速度对熔化时间的影响明显降低。
文章引用
叶文兰,赵 明,姚 莉,方 强. 三维Y肋相变蓄热器的热性能数值模拟及分析
Numerical Simulation and Analysis of Thermal Performance of a Three-Dimensional Y-Ribbed Phase Change Heat Accumulator[J]. 建模与仿真, 2023, 12(03): 1735-1748. https://doi.org/10.12677/MOS.2023.123161
参考文献
- 1. Pu, L., Zhang, S.Q., Xu, L.L. and Li, Y.Z. (2020) Thermal Performance Optimization and Evaluation of a Radial Finned Shell-and-Tube Latent Heat Thermal Energy Storage Unit. Applied Thermal Engineering, 166, Article ID: 116753. https://doi.org/10.1016/j.applthermaleng.2019.114753
- 2. Yu, C., Wu, S.C., Huang, Y.P., et al. (2020) Charging Per-formance Optimization of a Latent Heat Storage Unit with Fractal Tree-Like Fins. Journal of Energy Storage, 30, Article ID: 101498. https://doi.org/10.1016/j.est.2020.101498
- 3. Alizadeh, M., Hosseinzadeh, Kh., Shahavi, M.H., et al. (2019) Solidification Acceleration in a Triplex-Tube Latent Heat Thermal Energy Storage System Using V-Shaped Fin and Nano-Enhanced Phase Change Material. Applied Thermal Engineering, 163, Article ID: 114436. https://doi.org/10.1016/j.applthermaleng.2019.114436
- 4. Alizadeh, M., Hosseinzadeh, Kh. and Ganji, D.D. (2019) In-vestigating the Effects of Hybrid Nanoparticles on Solid-Liquid Phase Change Process in a Y-Shaped Fin-Assisted LHTESS by Means of FEM. Journal of Molecular Liquids, 287, Article ID: 110931. https://doi.org/10.1016/j.molliq.2019.110931
- 5. 张峰鸣, 赵明. 基于多相变材料的分腔式蓄热器蓄热性能优化[J]. 太阳能学报, 2020, 41(7): 227-236.
- 6. 任智彬, 黄河, 高佳徐, 等. 三维套管式加肋相变蓄热单元的传热特性分析[J]. 动力工程学报, 2022, 42(7): 437-443.
- 7. 林道光, 毛永宁, 李小华. 内翅式套管相变蓄热器蓄热特性的模拟研究[J]. 流体机械, 2021, 49(2): 84-89.
- 8. Yuan, Y.P., Cao, X.L., Xiang, B., et al. (2016) Effect of Installation Angle of Fins on Melting Characteristics of Annular Unit for Latent Heat Thermal Energy Storage. Solar Energy, 136, 365-378. https://doi.org/10.1016/j.solener.2016.07.014
- 9. Voller, V.R. (1990) Fast Implicit Finite-Difference Method for the Analysis of Phase Change Problems. Numerical Heat Transfer Fundamentals, 17, 155-569. https://doi.org/10.1080/10407799008961737
- 10. Kamkari, B. and Shokouhmand, H. (2014) Experimental Investigation of Phase Change Material Melting in Rectangular Enclosures with Horizontal Partial Fins. International Journal of Heat and Mass Transfer, 78, 839-851. https://doi.org/10.1016/j.ijheatmasstransfer.2014.07.056
