Advances in Applied Mathematics
Vol.3 No.02(2014), Article
ID:13492,7
pages
DOI:10.12677/AAM.2014.32010
T-D猜想上多输出布尔函数构造
Yiran Chen, Meng ZhouKey Laboratory of Mathematics, Information and Behaviour of the Ministry of Education, School of Mathematics and System Science, Beihang University, Beijing
Email: 13352225@qq.com, zm1613@sina.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Feb. 18th, 2014; revised: Mar. 20th, 2014; accepted: Mar. 28th, 2014
ABSTRACT
An improvement has been made on the construction method of Boolean Functions and the relevant conclusions of combinatorial conjecture proposed by Ziran Tu. We generalized their results and extended to the vectorial case. A class of bent Boolean functions F with the maximum algebraic immunity is presented by a more general construction method. Then by modifying F, we get new vectorial balanced functions with optimum algebraic degree, good nonlinearity and good algebraic immunity even maximum algebraic immunity for some cases.
Keywords:Vectorial Boolean Functions, Algebraic Immunity, Bent Function, Balancedness, Nonlinearity

T-D猜想上多输出布尔函数构造
陈怡然,周 梦
北京航空航天大学数学与系统科学学院,数学、信息与行为教育部重点实验室,北京
Email: 13352225@qq.com, zm1613@sina.com
收稿日期:2014年2月18日;修回日期:2014年3月20日;录用日期:2014年3月28日

摘 要
本文针对基于涂自然等人提出的组合猜想上布尔函数的构造方法和有关结论,将组合猜想和构造方法一般化,并将其推广到多输出布尔函数上去,构造出具有最优代数免疫度的多输出bent函数F,同时通过修改F构造出具有好的非线性度、最优代数度和最优代数免疫度兼具的多输出平衡布尔函数函数。
关键词
多输出布尔函数,代数免疫度,Bent函数,平衡性,非线性度

1. 引言
布尔函数作为密码学的重要组成部分,随着信息时代的到来,其研究得到了快速发展。布尔函数按构造可分为单输出布尔函数和多输出布尔函数两种,单输出布尔函数一般用于流密码,而用于构成S-盒的向量布尔函数也叫做多输出布尔函数在分组密码和流密码都有着重要作用。2009年涂自然和邓映蒲提出了T-D猜想,构造出能抵抗代数攻击[1] -[4] 等多种攻击,具有最佳非线性性和代数免疫度[5] 的单输出布尔函数。2011年冯克勤等将其猜想和构造方法推广到多输出布尔函数中,构造出了在一定条件下非线性和代数免疫度很好的多输出布尔函数。后来又出现了基于T-D猜想的各种组合猜想,构造出了更多的密码学性质优异的单输出布尔函数,由此我们基于T-D猜想和其他组合猜想大胆构造出一个一般的组合猜想,并假设这个猜想也可以推广到多输出布尔函数中,从而同样可以构造出更多的密码学性质优异的多输出布尔函数,我们将系统的对这个假设进行验证。
本文主要有这几个部分:第2节介绍相关知识;第3节给出T-D猜想和相关新组合猜想;第4节给出了一类具有最优代数免疫度的偶数元多输出布尔函数的构造;第5节对此多输出布尔函数进行修改,并讨论它的平衡性和非线性度;第6节进行总结和展望。
2. 布尔函数基本知识
2.1. 单输出布尔函数
单输出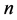 元布尔函数定义为:设
元布尔函数定义为:设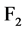 是二元有限域,
是二元有限域,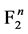 是
是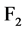 上的
上的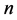 维向量空间,一个
维向量空间,一个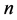 元布尔函数
元布尔函数 是从
是从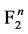 到
到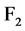 上的一个映射。
上的一个映射。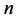 元布尔函数的全体记作
元布尔函数的全体记作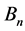 。一个
。一个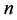 元布尔函数
元布尔函数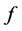 的基本表示方法是真值表表示,即
的基本表示方法是真值表表示,即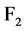 上的一个长为
上的一个长为 的向量:
的向量: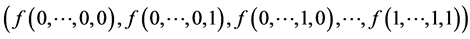 。每一个
。每一个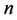 元布尔函数
元布尔函数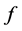 还可以唯一表示为
还可以唯一表示为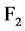 上的含
上的含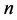 个变元的多项式,称之为
个变元的多项式,称之为 的代数正规型(Algebraic Normal Form, ANF):
的代数正规型(Algebraic Normal Form, ANF):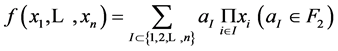 。非零布尔函数
。非零布尔函数 的代数次数
的代数次数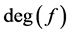 定义为代数正
定义为代数正
规型中系数非零项所含有最多的变元的个数,规定代数系数不超过1的布尔函数为仿射函数,全体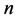 元仿射函数的集合记为
元仿射函数的集合记为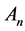 。设
。设 为
为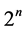 元有限域,则它可以看成
元有限域,则它可以看成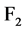 上的
上的 维向量空间。
维向量空间。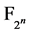 上的任意布尔
上的任意布尔
函数也可以表示成唯一的单变元多项式: 其中
其中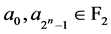 ,
, 对
对 ,且满足
,且满足 。此时
。此时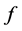 的代数次数
的代数次数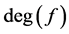 为
为 ,这里
,这里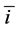 为
为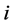 的二进制展开。
的二进制展开。
单输出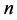 元布尔函数
元布尔函数 的支撑集定义为:
的支撑集定义为: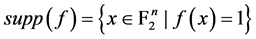 。支撑集
。支撑集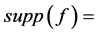 所含元素的个数称为
所含元素的个数称为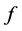 的Hamming重量,记为
的Hamming重量,记为 。若
。若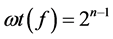 ,则称
,则称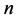 元布尔函数是平衡的。两个
元布尔函数是平衡的。两个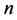 元布尔函数
元布尔函数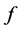 和
和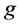 的Hamming距离
的Hamming距离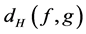 定义为
定义为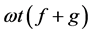 。
。
单输出布尔函数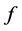 的非线性度定义为:
的非线性度定义为: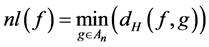 。
。
单输出布尔函数的Walsh谱定义为:令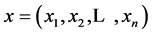 ,
, 都属于
都属于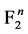 。记
。记 ,则Walsh谱
,则Walsh谱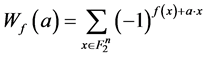 。对于
。对于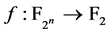 ,其
,其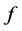 在
在 点的Walsh谱定义为:
点的Walsh谱定义为: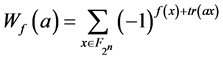 ,
,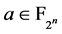 其中
其中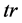 是从
是从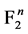 到
到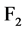 上的迹函数:
上的迹函数: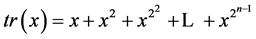 。对于
。对于 ,其
,其 在
在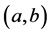 点的Walsh谱定义为:
点的Walsh谱定义为: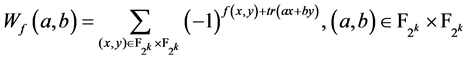 。一个布尔函数
。一个布尔函数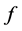 是平衡函数当且仅
是平衡函数当且仅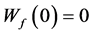 。
。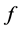 的非线性度也可以由Walsh谱给出:
的非线性度也可以由Walsh谱给出: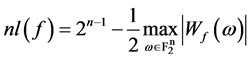 。对任意
。对任意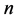 元布尔函数
元布尔函数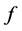 ,有
,有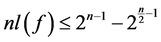 。达到这个上界的布尔函数称为Bent函数[6] 。
。达到这个上界的布尔函数称为Bent函数[6] 。
单输出布尔函数代数免疫度的定义:对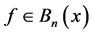 ,
,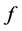 的零化子的集合记作:
的零化子的集合记作: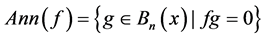 。布尔函数
。布尔函数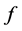 的代数免疫度(Algebraic Immunity)
的代数免疫度(Algebraic Immunity)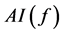 指的是:
指的是: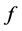 与
与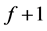 的非零零化子的最低次数,即
的非零零化子的最低次数,即 ,可以证明,
,可以证明,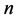 元布尔
元布尔
函数的代数免疫度不超过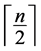 [3] [5] 。如果一个
[3] [5] 。如果一个 元布尔函数的代数免疫度恰好等于
元布尔函数的代数免疫度恰好等于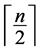 ,则称该函数具有最优代数免疫度或最大代数免疫度(Maximum Algebraic Immunity),简称MAI函数。
,则称该函数具有最优代数免疫度或最大代数免疫度(Maximum Algebraic Immunity),简称MAI函数。
2.2. 多输出(向量)布尔函数
假设 ,多输出布尔函数定义为:
,多输出布尔函数定义为: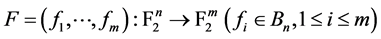 。
。
如果对所有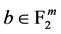 ,
,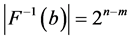 称布尔函数
称布尔函数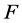 是平衡的,其中
是平衡的,其中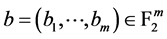 ,
,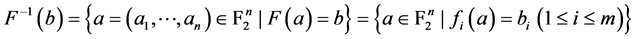 ,我们知道布尔函数
,我们知道布尔函数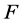 是平衡的当且仅当布尔函数
是平衡的当且仅当布尔函数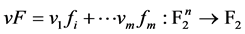 是平衡的,对每个
是平衡的,对每个 。
。
布尔函数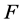 的非线性度定义为:
的非线性度定义为:
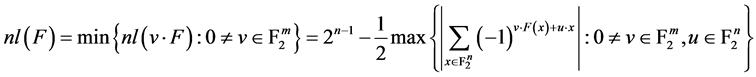 已经证明出对每个
已经证明出对每个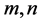 ,
,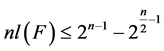 。如果
。如果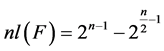 ,称布尔函数
,称布尔函数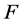 为bent函数,只有可能当且仅当
为bent函数,只有可能当且仅当 是偶数且
是偶数且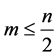 时得到。从定义可以很容易得到布尔函数
时得到。从定义可以很容易得到布尔函数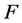 为bent函数当且仅当对每个
为bent函数当且仅当对每个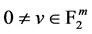 ,函数
,函数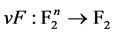 是bent函数。
是bent函数。
布尔函数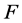 的代数度定义为:
的代数度定义为: ,如果
,如果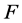 是平衡的,那么所有
是平衡的,那么所有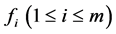 都是平衡的,所以
都是平衡的,所以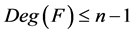 。
。
布尔函数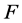 的代数免疫度定义为
的代数免疫度定义为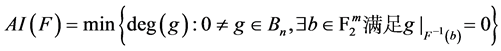 。令
。令 是满足
是满足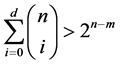 的最小整数,那么已经证明
的最小整数,那么已经证明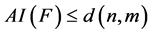 ,取等号时布尔函数
,取等号时布尔函数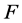 取得最优代数免疫度。
取得最优代数免疫度。
3. 一些组合猜想
猜想1[7] (T-D猜想) 设 ,
,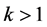 ,对任意
,对任意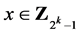 ,把
,把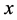 展开成
展开成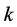 位二进制数,用
位二进制数,用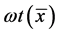 表示
表示 的展开式中1的个数,对任意
的展开式中1的个数,对任意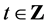 ,
,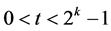 ,令
,令
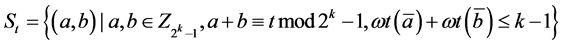 则
则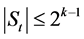 。
。
[7] 中涂自然和邓映蒲说明了虽然至今无法精确证明此猜想,但已经可以证明当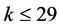 时猜想成立。D.Tang等人在文献[8] 又给出了一个类似的新组合猜想:
时猜想成立。D.Tang等人在文献[8] 又给出了一个类似的新组合猜想:
猜想2[8] 设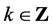 ,
, 。对任意
。对任意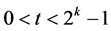 ,定义
,定义
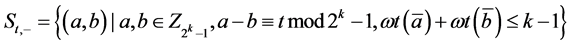 则
则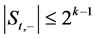 。
。
这个猜想已经被证明[9] ,同时也提出了下面的猜想:
猜想3[8] 设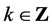 ,
,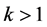 ,
,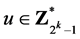 。对任意
。对任意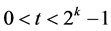 ,定义:
,定义:
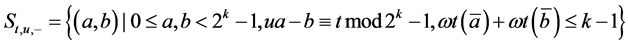 ,则
,则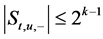 。
。
并且,当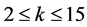 时,文献[8] 对
时,文献[8] 对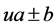 的情况给出了验证。可见猜想3包括了猜想2这种特殊情况,下面我们在这里将给出一个更一般化的组合猜想:
的情况给出了验证。可见猜想3包括了猜想2这种特殊情况,下面我们在这里将给出一个更一般化的组合猜想:
猜想4设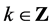 ,
, ,
,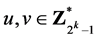 。对任意
。对任意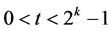 ,定义:
,定义:
 ,则
,则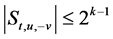 。
。
证明文献[10] 中已证明了 的情况等同于
的情况等同于 的情况,这里也可以用同样的手段得出猜想4等同于猜想3。
的情况,这里也可以用同样的手段得出猜想4等同于猜想3。
在文献[11] 中冯克勤等将组合猜想1推广到了多输出布尔函数上,于是大胆假设这几种猜想都同样可以推广到多输出布尔函数中,这里对猜想4进行推广:
猜想5令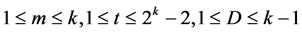 ,定义:
,定义:
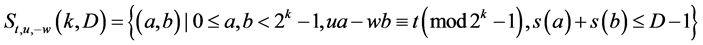 ;
;
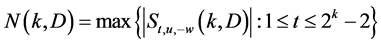 ,
,
其中对于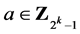 ,
,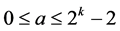 ,
,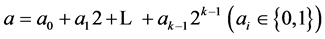 ,
,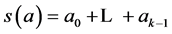 。令
。令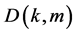 是最大的整数
是最大的整数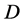 那么
那么 。
。
4. 最优代数免疫度的多输出布尔函数
根据上述猜想,和文献[11] 中的构造,给出了一个一般的构造:
构造1令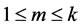 ,
,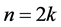 ,
,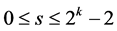 。
。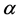 为
为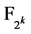 的本原元,
的本原元,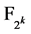 是下列
是下列 个不相交子列的并集:
个不相交子列的并集: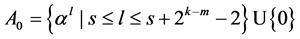 ;
; 。
。
每个整数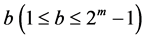 有2进制展开
有2进制展开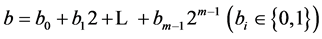 ,相当于向量
,相当于向量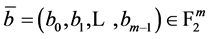 。对于每个
。对于每个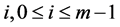 ,我们定义对
,我们定义对 ,
, ,
,
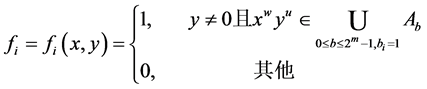 那么构造布尔函数
那么构造布尔函数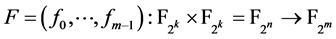 。
。
4.1. 代数免疫度
定理1:设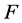 是构造算法1中的多输出布尔函数,则
是构造算法1中的多输出布尔函数,则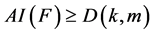 ,特别的,当
,特别的,当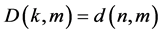 时
时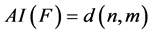 。
。
证明为了证明 ,我们只需要证明如果
,我们只需要证明如果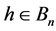 满足
满足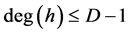 和至少有一个
和至少有一个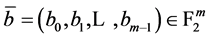 满足
满足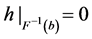 ,那么
,那么 。我们将
。我们将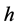 表示为
表示为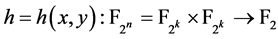 ,
,
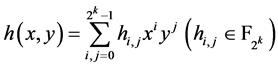 。
。
由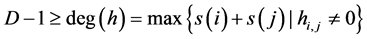 我们知道
我们知道 。
。
因为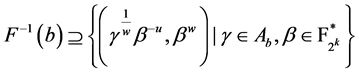 ,所以
,所以
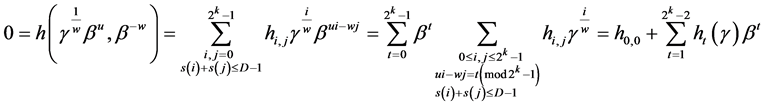
其中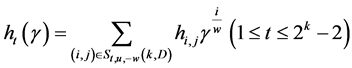 ,集合
,集合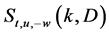 是猜想5中定义的。
是猜想5中定义的。
考虑多项式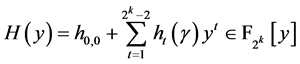 ,我们知道对所有的
,我们知道对所有的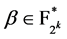 ,
,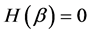 。因此我们得到
。因此我们得到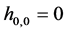 且
且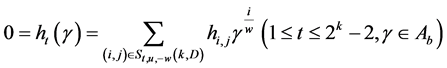 。
。
由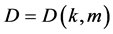 的定义,我们知道
的定义,我们知道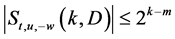 ,令
,令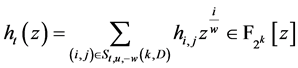 ,
,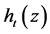 中
中
非零系数 的个数最多为
的个数最多为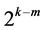 ,又对所有
,又对所有 ,
,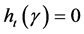 。如果
。如果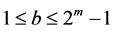 ,
,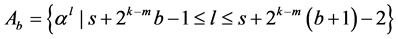 ,由BCH码[12] 中BCH界知
,由BCH码[12] 中BCH界知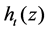 的所有系数都是0。当
的所有系数都是0。当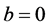 时,
时,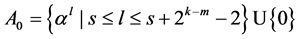 ,如果
,如果 ,那么
,那么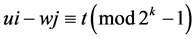 相当于
相当于 此时
此时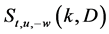 是空集。如果
是空集。如果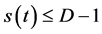 不妨设
不妨设 ,容易知道
,容易知道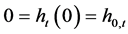 ,所以
,所以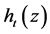 中非零系数的个数最多为
中非零系数的个数最多为 ,而
,而 ,得到
,得到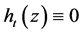 。综上,
。综上,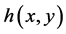 的所有系数
的所有系数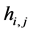 都等于0,即
都等于0,即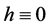 。
。
注:证明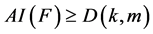 的过程中没有用到
的过程中没有用到 ,因此对任意
,因此对任意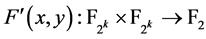 满足
满足 ,我们有不论
,我们有不论 的值是多少
的值是多少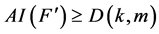 。
。
4.2. 一类具有最优代数免疫度的Bent函数
我们可以看出构造1中定义的布尔函数的非线性度随着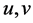 取值的变化而变化,我们考虑它可否成为非线性度达到最高的bent函数。
取值的变化而变化,我们考虑它可否成为非线性度达到最高的bent函数。
引理1:设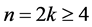 ,
,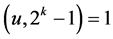 。
。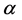 为
为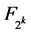 的本原元,设
的本原元,设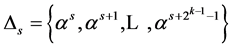 。其中
。其中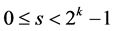 ,
,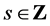 。定义
。定义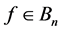 如下:
如下: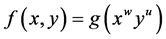 ,
, 其中
其中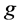 是定义在
是定义在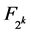 上满足
上满足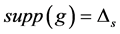 的布尔函数。当
的布尔函数。当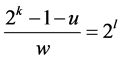 ,
,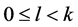 时,
时,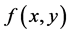 是bent函数。
是bent函数。
证明:我们仅需计算 。因为
。因为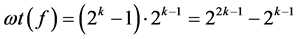 ,显然
,显然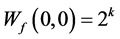 。
。 且
且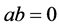 时
时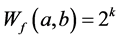 。
。
对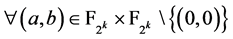 ,有
,有
 。
。
令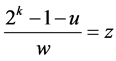 易知
易知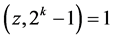 ,那么一定存在唯一的
,那么一定存在唯一的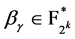 ,使得
,使得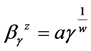 ,而
,而 ,所以
,所以 ,于是我们有:
,于是我们有: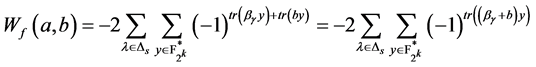 。
。
1)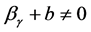 ,即对任意
,即对任意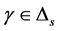 ,
,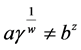 ,
,
 (因为
(因为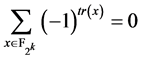 )
)
2)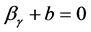 ,即对一些
,即对一些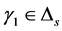 ,
,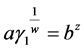 ,
,
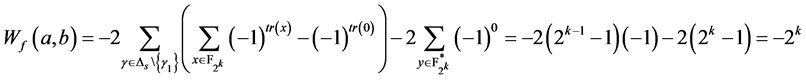
注意到最多只存在一个 满足
满足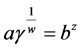 ,对
,对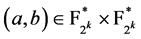 。
。
综上,对任意 ,
, 所以
所以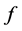 是bent函数。
是bent函数。
注:事实上,这类bent函数是Dillon提出的PS类函数[13] 。因为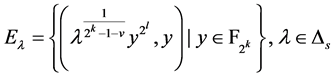
是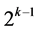 个
个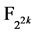 的
的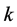 维线性子空间且对于
维线性子空间且对于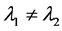 ,
,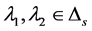 有
有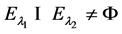 。
。
定理2令 是构造1中定义的多输出布尔函数,若
是构造1中定义的多输出布尔函数,若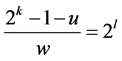 ,
,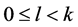 ,那么
,那么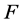 是具有最优代数免疫度的bent函数,
是具有最优代数免疫度的bent函数,
证明:要证明F是bent函数,我们需要证明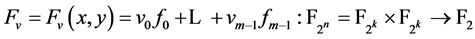 对每个
对每个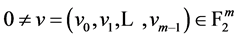 是bent函数。由
是bent函数。由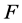 的定义知对于每个
的定义知对于每个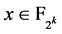 ,
,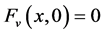 。假设
。假设 ,
,
那么对于每个 都存在
都存在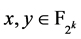 满足:
满足: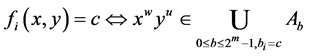 ,从而对每个
,从而对每个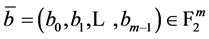 ,
,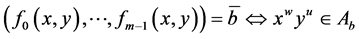 ,
,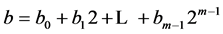 。
。
因此,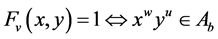 对每个
对每个 满足
满足 。
。
我们定义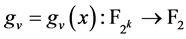 为
为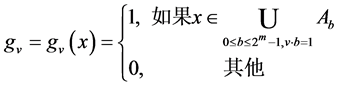 那么对于
那么对于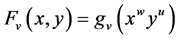
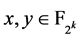 。
。
对每个非零向量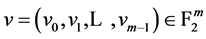 ,方程
,方程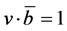 的解
的解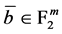 的个数是
的个数是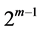 因此
因此 ,即
,即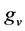 是平衡的,由引理1知对每个
是平衡的,由引理1知对每个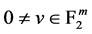 ,
,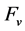 是bent函数,因此
是bent函数,因此 是bent函数。
是bent函数。
5. 具有最优代数免疫度的平衡布尔函数
平衡性是布尔函数又一个重要的密码学性质,一个非平衡的布尔函数其输出序列的随机性是最不理想的吗,易受区分攻击,bent函数有最大的非线性度,但不是平衡的。这个部分我们将把构造1中布尔函数改造为平衡函数,同时也兼具好的代数免疫度和非线性度。
构造2令 ,
,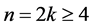 ,
, ,
, 是
是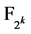 的两个本原元。令
的两个本原元。令 其中
其中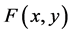 是构造1中定义的布尔函数,
是构造1中定义的布尔函数,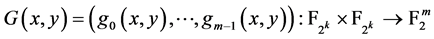 定义为:
定义为:
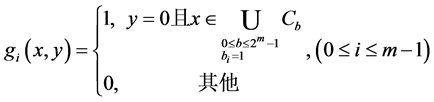
其中
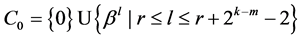 ,
,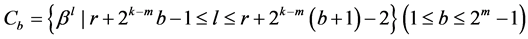 。
。
那么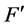 是平衡的,且
是平衡的,且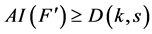 ,
,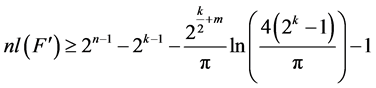 。
。
证明:因为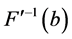 和
和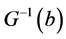 对任意
对任意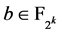 是不相交的所以
是不相交的所以 故
故 是平衡的。
是平衡的。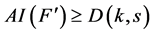 的证明参照定
的证明参照定
理1后的注。现在只需证明 。
。
注意到 ,其中:
,其中:
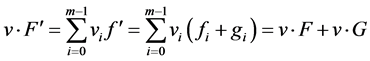 ,
,
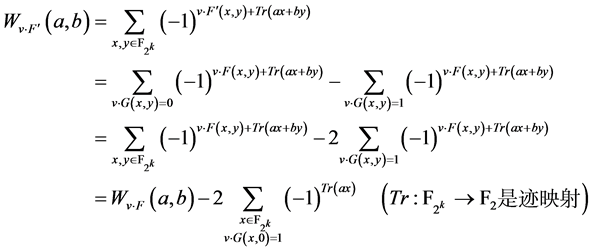
因为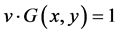 相当于
相当于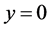 且
且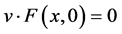 。
。
如果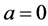 ,那么
,那么 。
。
而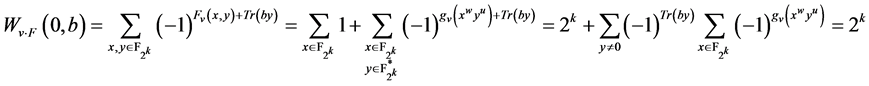 (
(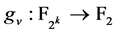 是证明定理1中构造的平衡函数)。
是证明定理1中构造的平衡函数)。
又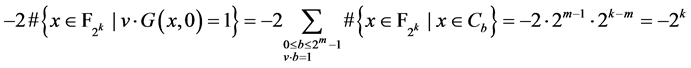 所以
所以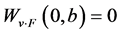 。
。
我们已经知道对于 ,
,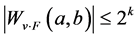 且
且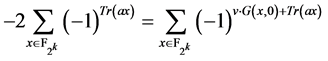 ,由文献[14] 中定理3的证明我们知道
,由文献[14] 中定理3的证明我们知道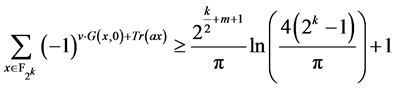 。因此
。因此 。
。
6. 总结与展望
我们发现当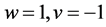 时,所构造的多输出布尔函数就是文献[11] 中的函数,也就是冯克勤教授等通过对T-D猜想的推广构造出的多输出布尔函数。这里本文的推广给出了可能的更一般的多输出布尔函数构造方法,能提供更多的布尔函数供研究所用,在本文中,我们基于T-D猜想构造出一般化的组合猜想,并将构造方法推广到多输出布尔函数中,构造出具有最优代数免疫度的多输出布尔函数,这时可以通过确定
时,所构造的多输出布尔函数就是文献[11] 中的函数,也就是冯克勤教授等通过对T-D猜想的推广构造出的多输出布尔函数。这里本文的推广给出了可能的更一般的多输出布尔函数构造方法,能提供更多的布尔函数供研究所用,在本文中,我们基于T-D猜想构造出一般化的组合猜想,并将构造方法推广到多输出布尔函数中,构造出具有最优代数免疫度的多输出布尔函数,这时可以通过确定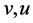 的取值来讨论布尔函数的各种密码学性质,这样更多的布尔函数可被发现并应用。本文还存在一些待解决的问题,如这种构造方法是否比已有方法更优还待考证,不同
的取值来讨论布尔函数的各种密码学性质,这样更多的布尔函数可被发现并应用。本文还存在一些待解决的问题,如这种构造方法是否比已有方法更优还待考证,不同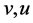 取值时构造出的布尔函数性质的比较,这类构造方法构造出的布尔函数与已有的多输出布尔函数的比较等等,都是以后的研究重点。
取值时构造出的布尔函数性质的比较,这类构造方法构造出的布尔函数与已有的多输出布尔函数的比较等等,都是以后的研究重点。
致 谢
本文工作受国家自然科学基金资助,涂自然等的研究成果给予了深厚的研究基础和启发,同时张喆琳硕士提供了重要的参考文献,在此一并致以衷心的感谢。
项目基金
国家自然科学基金NSFC 11271040资助项目。
参考文献 (References)
- Armknecht, F. (2004) Improving fast algebraic attacks: FSE 2004. Springer Verlag, 65-82.
- Batten, L.M. (2004) Algebraic attacks over GF(q): Cryptology-INDOCRYPT 2004. Springer Verlag, 84-91.
- Courtois, N. and Meier, W. (2003) Algebraic attacks on stream ciphers with linear feedback: Cryptology-EUROCRYPT 2003. Springer Verlag, 345-359.
- Courtois, N. (2003) Fast algebraic attacks on stream ciphers with linear feedback: Advances in Cryptology-CRYPTO 2003. Springer Verlag, 176-194.
- Meier, W., Pasalic, E. and Carlet, C. (2004) Algebraic attacks and decomposition of Boolean functions: CryptologyEUROCRYPT 2004. Springer Verlag, 474-491.
- Rothaus, O.S. (1976) On bent functions. Journal of Combinatorial Theory A, 20,300-305.
- Tu, Z. and Deng, Y. (2010) A conjecture about binary strings and its applications on constructing Boolean functions with optimal algebraic immunity. Designs, Codes and Cryptography, 1-14.
- Tang, D., Carlet, C. and Tang, X. Highly nonlinear Boolean functions with optimum algebraic immunity and good behavior against fast algebraic attacks. Cryptology ePrint Archive. http://eprint.iacr.org/2011/366.pdf
- Cohen, G. and Flori, J.P. On a generalized combinatorial conjecture involving addition mod 2k-1. Cryptology ePrint Archive. http://eprint.iacr.org/2011/400.pdf
- Jin, Q., Liu, Z., Wu, B. and Zhang, X. A general conjecture similar to T-D conjecture and its applications in constructing Boolean functions with optimal algebraic immunity. Cryptology ePrint Archive. http://eprint.iacr.org/2011/515.pdf
- Feng, K. and Yang, J. (2011) Vectorial Boolean functions with good cryptographic properties. International Journal of Foundations of Computer Science, 22, 1271-1282.
- MacWilliams, F.J. and Sloane, N.J.A. (1977) The Theory of Error-Correcting Codes. North-Holland, Amsterdam.
- Dillon, J.F. (1974) Elementary hadamard difference sets. Ph.D. Thesis, University of Maryland, College Park.
- Carlet, C. and Feng, K. (2009) An infinite class of balanced vectorial Boolean functions with optimal algebraic immunity and good nonlinearity. In: Xing, C., et al., Eds., Proceedings of the IWCC 2009, 1-11.