Advances in Applied Mathematics
Vol.04 No.04(2015), Article ID:16300,6
pages
10.12677/AAM.2015.44040
An Parabolic Differential Equation Inverse Problem with a Nonlinear Source Term
Hui Sun, Cui’e Xiao
School of Mathematics and Computation Sciences, Hunan City University, Yiyang Hunan
Received: Oct. 18th, 2015; accepted: Nov. 2nd, 2015; published: Nov. 9th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper is devoted to a class of inverse problem for parabolic differential equation with a nonlinear source term. Using the theories of monotone operator and the Sobolev embedding theorem, we verify the existence and uniqueness of weak solution for the direct problem as well as the existence of quasi-solutions of the inverse source problem in an appropriate class of admissible source functions.
Keywords:Nonlinear Parabolic Differential Equation, Direct Problem, Existence, Uniqueness, Inverse Problem, Quasi-Solution

具非线性来源项的抛物型方程反问题研究
孙惠,肖翠娥
湖南城市学院数学与计算科学学院,湖南 益阳

收稿日期:2015年10月18日;录用日期:2015年11月2日;发布日期:2015年11月9日

摘 要
本文主要研究一类具非线性来源项的抛物型方程,利用单调算子理论和Sobolev嵌入定理,证明了正问题解的存在性与唯一性。在合适的容许集中证明了反问题拟解的存在性。
关键词 :非线性抛物型方程,正问题,存在性,唯一性,反问题,拟解

1. 方程及基本假设
非线性抛物方程广泛存在于扩散现象、渗流理论、相变理论、生物化学以及生物群体动力学等领域,具有强烈的实际背景和重要的应用价值。近年来,随着计算方法和计算工具的不断发展,非线性抛物方程反问题得到了迅速发展,大量线性和非线性抛物型方程反问题以不同的形式出现在不同的应用背景下,如热传导、材料学、流体学、金融工程和数学物理及工程科学等。文献[1] -[7] 对非线性抛物方程及反问题进行了一定的研究。本文我们考虑如下具非线性来源项的抛物型方程:
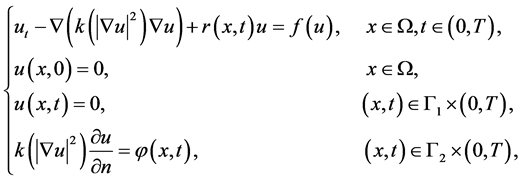 (1.1)
(1.1)
这里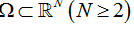 为有界开区域,边界
为有界开区域,边界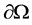 分片光滑,且
分片光滑,且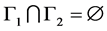 ,
,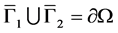 ,
,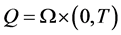 ,
,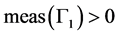 ,
,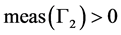 。
。
定义Sobolev空间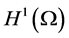 [8] 的闭子空间
[8] 的闭子空间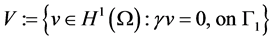 ,这里
,这里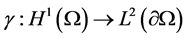 代表迹算子。在
代表迹算子。在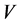 上赋以范数
上赋以范数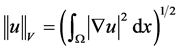 。令
。令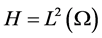 ,等同于它的对偶空间,则
,等同于它的对偶空间,则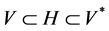 是稠密连续紧嵌入的[8] 。为方便起见,用
是稠密连续紧嵌入的[8] 。为方便起见,用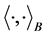 表示空间
表示空间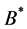 和
和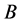 上的对偶积,用
上的对偶积,用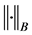 代表Banach空间
代表Banach空间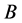 的模。记
的模。记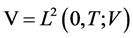 ,
, ,
,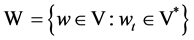 ,
,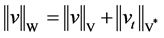 。则空间
。则空间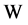 为可分自反的Banach空间,嵌入
为可分自反的Banach空间,嵌入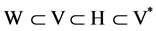 是连续嵌入,
是连续嵌入,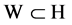 是紧嵌入。
是紧嵌入。
对于非线性源项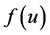 ,我们作如下假设:
,我们作如下假设:
(A1) 泛函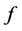 有界,即把有界集映为有界集;
有界,即把有界集映为有界集;
(A2) 函数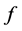 满足Lipschitz条件,即存在
满足Lipschitz条件,即存在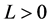 ,使得对任意的
,使得对任意的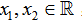 ,都有
,都有
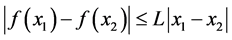 .
.
相应地,系数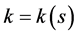 依赖于解的梯度,它通常用来描述Hencky物质材料性质。不失一般性,我们对系数
依赖于解的梯度,它通常用来描述Hencky物质材料性质。不失一般性,我们对系数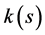 及
及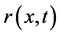 作如下假设:
作如下假设:
(A3)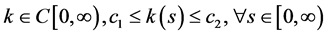 ;
;
(A4)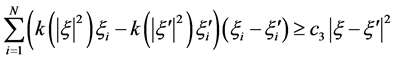 ;
;
(A5) 存在正常数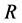 ,使得
,使得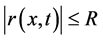 ,
,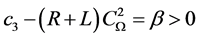
这里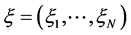 ,
,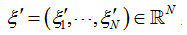 ,
,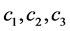 为正的常数,
为正的常数, 是Poincaré常数。
是Poincaré常数。
定义算子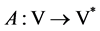 ,
,
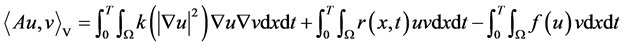 。 (1.2)
。 (1.2)
定义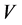 上有界线性泛函
上有界线性泛函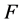 ,
,
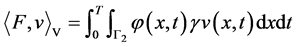 。 (1.3)
。 (1.3)
定义算子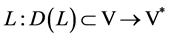 ,
,
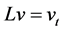 。 (1.4)
。 (1.4)
这里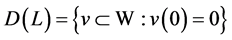 ,算子
,算子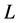 是线性稠密定义的极大单调算子([8] , p. 845)。从而问题(1.1)可表示为抽象算子方程:
是线性稠密定义的极大单调算子([8] , p. 845)。从而问题(1.1)可表示为抽象算子方程:
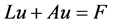 。 (1.5)
。 (1.5)
若已知源项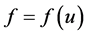 ,对于给定的函数
,对于给定的函数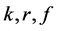 ,记(1.1)的解为
,记(1.1)的解为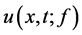 ,我们把从(1.1)中寻找解
,我们把从(1.1)中寻找解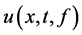 的问题,称为正问题(DP)。反之,若已知部分边界测量数据
的问题,称为正问题(DP)。反之,若已知部分边界测量数据
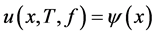
其中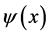 为已知数据。我们把寻找未知源项
为已知数据。我们把寻找未知源项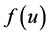 的问题称为未知源项的反问题,记为ISP。在实践中通常会用下列寻找最小化问题的解代替上述反问题ISP的解[9] ,即:
的问题称为未知源项的反问题,记为ISP。在实践中通常会用下列寻找最小化问题的解代替上述反问题ISP的解[9] ,即:
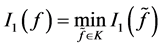 。 (1.6)
。 (1.6)
这里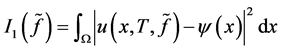 是辅助泛函,
是辅助泛函,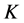 是函数
是函数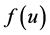 的容许集,最小化问题解称为上述反问题ISP的拟解。
的容许集,最小化问题解称为上述反问题ISP的拟解。
2. 正问题
为了得到问题(1.1)正问题弱解的存在唯一性,我们先给出几个定理和引理。
定理2.1 若条件(A2),(A3),(A5)成立,则算子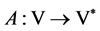 是次连续的。
是次连续的。
证明:假设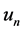 在
在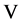 中强收敛到
中强收敛到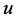 ,任取
,任取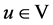 ,直接计算可得
,直接计算可得
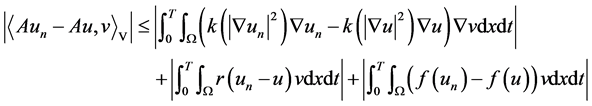
另一方面,由假设条件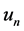 在
在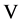 中强收敛到
中强收敛到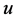 ,可以推出
,可以推出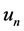 在
在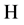 中强收敛到
中强收敛到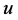 ,以及
,以及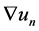 在
在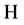 中强收敛到
中强收敛到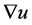 ,从而结合假设条件(A2),(A3),(A5)以及Lebesgue控制收敛定理不难推导出
,从而结合假设条件(A2),(A3),(A5)以及Lebesgue控制收敛定理不难推导出
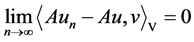 ,
,
即有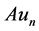 在
在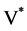 中弱收敛到
中弱收敛到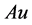 ,从而
,从而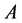 次连续。
次连续。
定理2.2 若条件(A2),(A4),(A5)成立,则算子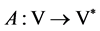 是强单调的。
是强单调的。
证明:任取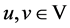 ,根据假设条件(A2),(A4),(A5),有
,根据假设条件(A2),(A4),(A5),有
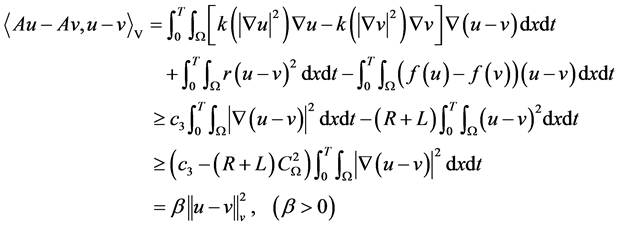 (2.1)
(2.1)
从而算子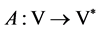 强单调。
强单调。
引理2.3 ([8] , p. 867)设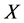 为Banach空间,算子
为Banach空间,算子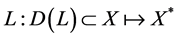 极大单调(定义域
极大单调(定义域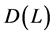 是
是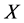 的非空凸闭集),算子
的非空凸闭集),算子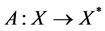 有界、伪单调、次连续,并且存在点
有界、伪单调、次连续,并且存在点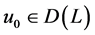 ,使得,
,使得,
当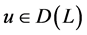 ,
,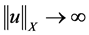 时,
时,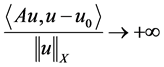 。(2.2)
。(2.2)
那么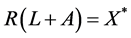 ,即对任意的
,即对任意的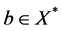 ,存在
,存在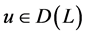 ,使得
,使得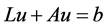 。
。
定理2.4 若条件(A1)~(A5)成立,则正问题(1.1)存在唯一解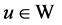 ,并且有先验估计:存在常数
,并且有先验估计:存在常数 ,使得
,使得
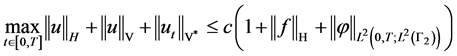 (2.3)
(2.3)
证明:根据假设条件(A1),(A3),(A5)可知, 是有界算子。由定理2.1和定理2.2,算子
是有界算子。由定理2.1和定理2.2,算子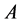 是单调次连续算子,从而是伪单调算子(见[8] P.586)。此外,令
是单调次连续算子,从而是伪单调算子(见[8] P.586)。此外,令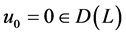 ,则
,则

因此,类似于(2.1)式的证明(取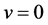 ),可以推出
),可以推出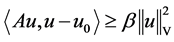 ,从而强制性条件(2.2)成立。因此,算子
,从而强制性条件(2.2)成立。因此,算子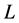 和
和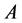 满足引理2.3中的条件,故存在
满足引理2.3中的条件,故存在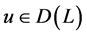 满足式(1.5),即正问题的解存在。
满足式(1.5),即正问题的解存在。
另一方面,由算子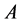 的强单调性不难推出(1.1)的解还是唯一的。
的强单调性不难推出(1.1)的解还是唯一的。
下面验证先验估计(2.3)。令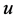 是(1.1)的解,在(1.5)式两边关于
是(1.1)的解,在(1.5)式两边关于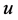 做内积可得
做内积可得
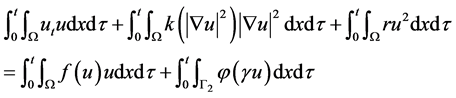 (2.4)
(2.4)
因为
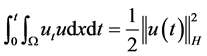
并且
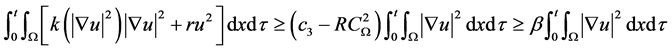
又根据Young不等式及Poincaré不等式,有
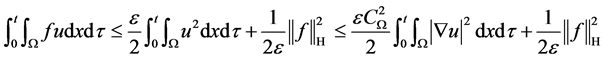
根据迹算子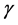 的有界性及Young不等式
的有界性及Young不等式
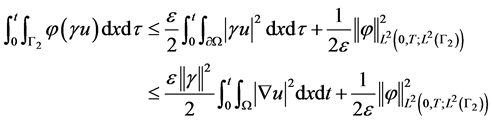
因此,结合式(2.4)并选取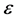 充分小,就可以存在常数
充分小,就可以存在常数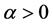 ,使得
,使得
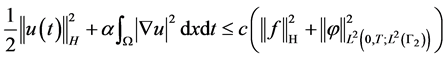 (2.5)
(2.5)
另一方面,由方程(1.5)可得
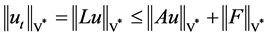 , (2.6)
, (2.6)
从而由(2.5),(2.6)以及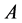 和
和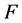 的有界性可以推出先验估计(2.3)。
的有界性可以推出先验估计(2.3)。
3. 反问题拟解的存在性
本节给出问题(1.1)反问题拟解的存在性。
定理3.1假设条件(A1)~(A5)成立,定义容许集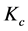 = {
= {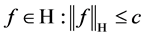 ,
,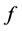 满足条件(A1),(A2)},则反问题(1.6)在
满足条件(A1),(A2)},则反问题(1.6)在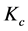 中至少存在一个拟解。
中至少存在一个拟解。
证明:因为任取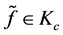 ,
,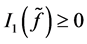 ,即
,即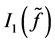 有下界,故存在下确界。设
有下界,故存在下确界。设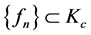 为
为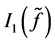 的极小化序列,即
的极小化序列,即
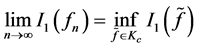
根据定理2.4,对任意的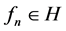 ,正问题(1.1)存在解
,正问题(1.1)存在解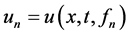 ,并满足先验估计式(2.3)。又因为
,并满足先验估计式(2.3)。又因为 ,故存在常数
,故存在常数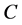 ,对
,对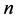 一致的有
一致的有
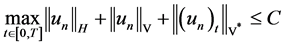 。
。
从而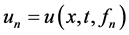 在
在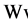 中有界,故存在弱收敛的子列(仍用原记号),不妨设
中有界,故存在弱收敛的子列(仍用原记号),不妨设 在
在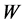 中弱收敛到
中弱收敛到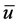 。由Aubin-Lions紧嵌入定理,
。由Aubin-Lions紧嵌入定理, 到
到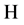 的嵌入是紧嵌入,故有
的嵌入是紧嵌入,故有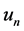 在
在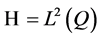 中强收敛到
中强收敛到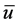 。
。
另一方面,因为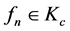 ,所以不妨设
,所以不妨设 在
在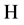 中弱收敛到
中弱收敛到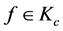 。根据定理2.4,对
。根据定理2.4,对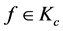 ,存在唯一解
,存在唯一解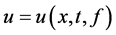 。又因为由
。又因为由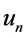 在
在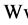 中弱收敛到
中弱收敛到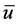 ,
,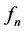 在
在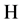 中弱收敛到
中弱收敛到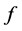 以及
以及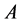 算子的伪单调次连续性质,可以推出
算子的伪单调次连续性质,可以推出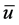 也满足(1.5)式,因此,由解的唯一性可知
也满足(1.5)式,因此,由解的唯一性可知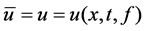 。
。
接下来我们将证明:
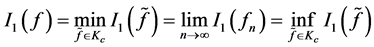 。 (3.1)
。 (3.1)
事实上,由于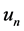 和
和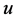 都满足式(1.5),两式相减并与
都满足式(1.5),两式相减并与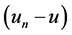 做内积,我们有
做内积,我们有
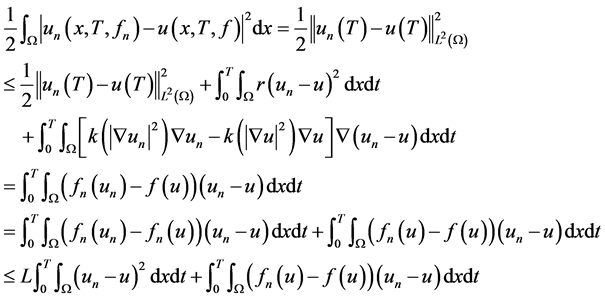 (3.2)
(3.2)
又因为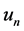 在
在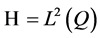 中强收敛到
中强收敛到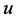 ,
,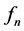 在
在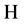 中弱收敛到
中弱收敛到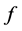 ,从而
,从而
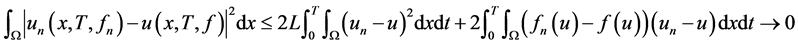
因此,
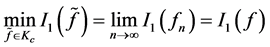
定理证毕。
基金项目
国家自然科学基金资助项目(11371125),湖南省教育厅资助科研项目(13A013, 13C127),湖南城市学院资助科研项目(2013xj009)。
文章引用
孙惠,肖翠娥. 具非线性来源项的抛物型方程反问题研究
An Parabolic Differential Equation Inverse Problem with a Nonlinear Source Term[J]. 应用数学进展, 2015, 04(04): 320-325. http://dx.doi.org/10.12677/AAM.2015.44040
参考文献 (References)
- 1. Xiao, C.E., Liu, J.B. and Liu, Y.L. (2011) An Inverse Pollution Problem in Porous Media. Applied Mathematics and Com-putation, 218, 3649-3653. http://dx.doi.org/10.1016/j.amc.2011.09.006
- 2. 李景. 不适定问题的正则化方法[D]: [博士学位论文]. 长沙: 中南大学, 2009.
- 3. Liu, Z.H. and Wang, B.Y. (2009) Coefficient Identification in Parabolic Equa-tions. Applied Mathematics and Computation, 209, 379-390. http://dx.doi.org/10.1016/j.amc.2008.12.062
- 4. Hua, O.Y., Hasanov, A. and Hai, L.Z. (2008) Inverse Coefficient Problems for Nonlinear Parabolic Differential Equations. Acta Mathematica Sinica, English Series, 24, 1617-1624. http://dx.doi.org/10.1007/s10114-008-6384-0
- 5. Liu, Z.H. (2000) On the Solvability of Degenerate Quasilinear Parabolic Equations of Second Order. Acta Mathematica Sinica, 16, 313-324. http://dx.doi.org/10.1007/s101140000052
- 6. Liu, Z.H. (2005) On Doubly Degenerate Quasilinear Parabolic Equations of Higher Order. Acta Mathematica Sinica, 21, 197-208. http://dx.doi.org/10.1007/s10114-004-0415-2
- 7. Liu, Z.H. (1999) Identification of Parameters in Semilinear Parabolic Equations. Acta Mathematica Scientia, 19, 175- 180.
- 8. Zeidler, E. (1990) Nonlinear Functional Analysis and Its Applications II A/B. Springer, New York.
- 9. Tikhonov, A. and Arsenin, V. (1977) Solutions of Ill-Posed Problems. Wiley, New York.