Advances in Applied Mathematics
Vol.05 No.01(2016), Article ID:16961,9
pages
10.12677/AAM.2016.51003
Stability Analysis of an Impulsively Population Control Model in Periodical Environment
Na Wang, Zhichun Yang
School of Mathematical Sciences, Chongqing Normal University, Chongqing

Received: Jan. 28th, 2016; accepted: Feb. 19th, 2016; published: Feb. 22nd, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In the paper, we study the stability of pest-extinction periodic solutions of an impulsively population control model in periodical environment. First, we formulate a plant-pest-natural enemy model in periodical environment with harvesting, spraying and releasing at different moments. Then, we obtain pest-extinction periodic solutions. Some sufficient conditions for local stability and globally stability of pest-extinction periodic solutions are determined by the comparison technique of impulsive differential equations and the Floquet theory.
Keywords:Impulsively, Periodical Environment, Pest-Extinction Periodic Solution, Stability

一类具有周期系数的脉冲种群模型稳定性分析
王娜,杨志春
重庆师范大学数学科学学院,重庆

收稿日期:2016年1月28日;录用日期:2016年2月19日;发布日期:2016年2月22日

摘 要
本文主要研究一类具有周期系数的脉冲种群控制模型的害虫灭绝周期解的稳定性问题。首先,建立在不同时刻收割庄稼、喷洒农药和释放天敌的一类具有周期系数的植物害虫天敌的脉冲控制模型。然后得到脉冲控制模型的两个害虫灭绝周期解,利用线性化方法、比较原理以及Floquet原理,分别给出害虫灭绝周期解局部稳定性和全局稳定性的一些充分条件。
关键词 :脉冲,周期系数,害虫灭绝周期解,稳定性

1. 引言
在过去几年,许多农民采用农药控制、生物控制或者物理控制治理害虫。随着科技的发展,害虫治理有了更加合理的办法,如通过释放该害虫的自然天敌来遏制害虫的生长。最近,不少学者建立了具有脉冲害虫治理的捕食种群模型,并进行动态行为分析[1] -[9] 。Jiao等 [1] 建立了一类在不同脉冲时刻捕捞和释放的捕食-食饵模型,给出了害虫灭绝周期解的局部稳定性、全局稳定性和系统持久性的充分条件。Kunwer等 [2] 建立了不同年龄阶段天敌的三种群模型,获得了害虫灭绝周期解稳定性存在的充分条件和模型的持久性。Paul等 [3] 建立了一类在不同脉冲时刻脉冲扰动的植物害虫天敌模型,研究了模型正周期性的存在性以及稳定性存在的条件。
另一方面,现实世界中种群环境通常是随时间周期变化的,考虑具有周期系数模型更加符合实际。Yang [4] 建立了具有脉冲周期系数和Holling III类功能反应的捕食系统,并得到了系统的持续生存性、周期解的存在唯一性和全局吸引性。Liu等 [5] 研究了一类具有周期系数的单种群模型,得出了模型稳定性的条件。Tang等 [6] 研究了一类具有周期系数的捕食模型,获得了周期解稳定性的充分条件。
据作者所知,同时考虑在不同时刻进行收割庄稼、喷洒农药和释放天敌,并具有周期系数的捕食-食饵模型几乎未见报道,其动态性质研究显得非常重要。
本文建立了一类在不同脉冲时刻收割庄稼、喷洒农药和投放天敌,且具有周期系数的植物–害虫–天敌的脉冲控制模型如下:
 (1)
(1)
其中, 表示
表示 时刻植物的密度;
时刻植物的密度;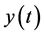 表示
表示 时刻害虫的密度;
时刻害虫的密度; 表示
表示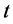 时刻天敌的密度。
时刻天敌的密度。 为植物的密度变化的内禀生长率,
为植物的密度变化的内禀生长率, 为植物的的环境容纳量函数,
为植物的的环境容纳量函数,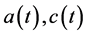 分别为植物和害虫的功能反应函数,
分别为植物和害虫的功能反应函数, 分别为植物和害虫的转化率及功能反应乘积函数,
分别为植物和害虫的转化率及功能反应乘积函数, 分别为害虫和天敌的死亡函数;其中
分别为害虫和天敌的死亡函数;其中 ,且都是
,且都是 周期函数;
周期函数; 表示释放天敌、喷洒农药和收割庄稼的周期;
表示释放天敌、喷洒农药和收割庄稼的周期; 表示
表示 时刻植物的收割率,
时刻植物的收割率, 分别表示
分别表示 时刻喷洒农药对害虫和天敌的损失率;
时刻喷洒农药对害虫和天敌的损失率; 表示
表示 时刻释放天敌的数量。
时刻释放天敌的数量。
我们主要利用线性化方法、脉冲微分方程的比较原理以及Floquet原理,讨论周期系统(1)的两个害虫灭绝周期解局部稳定性和全局稳定性的一些充分条件。
2. 预备知识
为了获得本文主要结论,本节将给出一些引理。
考虑脉冲微分方程
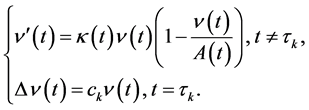 (2)
(2)
假设上述系统是T周期的,即存在 使得
使得
 (3)
(3)
且满足:
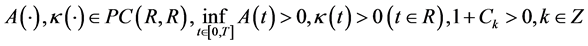 (4)
(4)
引理2.1 [10] 假设条件(3),(4)成立,若
 (5)
(5)
则系统有唯一的全局渐近稳定的正周期解 满足
满足 和
和 ,其中
,其中
 或者
或者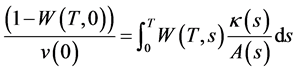 。
。
引理2.2 [11] 考虑如下的脉冲控制系统
 (6)
(6)
其中 。则系统有唯一的周期解
。则系统有唯一的周期解 ,且任意解
,且任意解 ,当
,当 有
有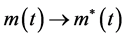 ,其中
,其中

证明 由系统(6)有

利用系统(6)的第二个和第三个式子,我们得到
 (7)
(7)
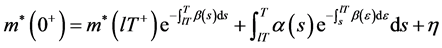 (8)
(8)
通过(7)和(8),有
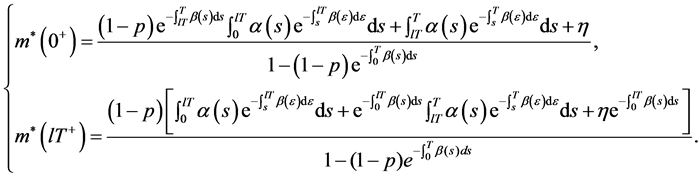
所以,可得系统(6)的周期解:

证毕。
3. 害虫灭绝周期解的稳定性
本节分析周期系统(1)的害虫灭绝的周期解的存在性,并给出周期解局部稳定性和全局稳定性的充分条件。
首先讨论系统(1)害虫灭绝周期解,即令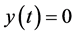 ,那么系统(1)将变为:
,那么系统(1)将变为:
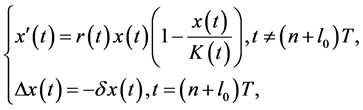 (9)
(9)
 (10)
(10)
根据引理2.1,如果

那么系统(9)有正周期解
 (11)
(11)
其中 。
。
利用引理2.2有系统(10)的周期解
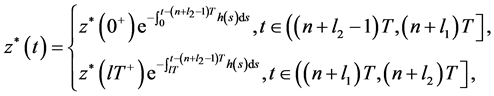 (12)
(12)
其中

由此可得系统(1)的两个害虫灭绝周期解 和
和 。下面我们分别讨论它们的稳定性问题。
。下面我们分别讨论它们的稳定性问题。
定理3.1 假设当 时,周期系统(1)的害虫灭绝周期解
时,周期系统(1)的害虫灭绝周期解 是局部稳定的;当
是局部稳定的;当 时,周期系统(1)的害虫灭绝周期解
时,周期系统(1)的害虫灭绝周期解 是不稳定的。
是不稳定的。
证明 假设 系统(1)的任意解,令
系统(1)的任意解,令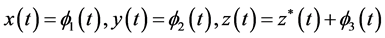 。将系统(1)在点
。将系统(1)在点 线性化得:
线性化得:
 (13)
(13)
设 是系统(13)的基解距阵,则有
是系统(13)的基解距阵,则有

考虑系统(13)的脉冲部分,有

和

令

则 的系统乘子为
的系统乘子为
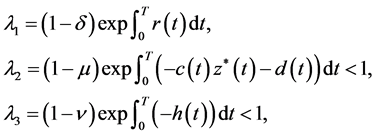
根据脉冲微分方程Floquet原理知,当 ,即
,即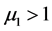 时害虫灭绝周期解
时害虫灭绝周期解 是局部稳定的。当
是局部稳定的。当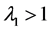 ,即
,即 时周期解
时周期解 是不稳定的。证毕。
是不稳定的。证毕。
下面我们讨论当 时,系统存在周期解
时,系统存在周期解 的稳定性。
的稳定性。
定理3.2 假设 ,如果
,如果
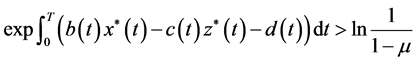 (14)
(14)
成立,则系统(1)的害虫灭绝周期解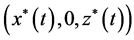 是不稳定的;如果
是不稳定的;如果
 (15)
(15)
成立,则系统(1)的害虫灭绝周期解 是局部稳定的。
是局部稳定的。
证明 类似定理3.1,将系统(1)在点 线性化的基解距阵有
线性化的基解距阵有
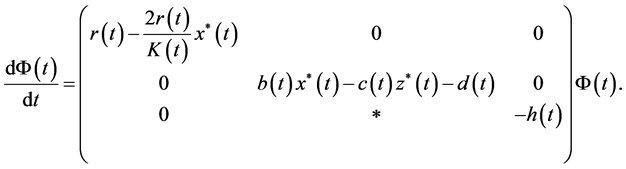
其中 且充分小。则
且充分小。则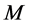 的系统乘子为
的系统乘子为

根据脉冲微分方程Floquet原理知,若 害虫灭绝周期解
害虫灭绝周期解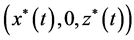 是不稳定的;若
是不稳定的;若 害虫灭绝周期解
害虫灭绝周期解 是局部稳定的。证毕。
是局部稳定的。证毕。
下面我们进一步得到 全局稳定性的充分条件。
全局稳定性的充分条件。
定理3.2 假设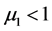 ,如果
,如果

成立,则系统(1)的害虫灭绝周期解 是全局渐近稳定的。
是全局渐近稳定的。
证明 假设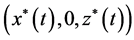 是系统(1)的任意解,则系统(1)可写作:
是系统(1)的任意解,则系统(1)可写作:
 (16)
(16)
由系统(16)第1个式子,得其比较系统
 (17)
(17)
由引理2.1和比较定理,有系统(17)存在周期解 且满足
且满足 当
当 ,其中
,其中 为方程(18)任意解。即存在整数
为方程(18)任意解。即存在整数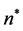 ,使得所有满足
,使得所有满足 ,且存在充分小的
,且存在充分小的 ,有
,有

类似地,考虑系统
 (18)
(18)
利用引理2.2,得系统(18)存在周期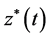 且满足
且满足 ,当
,当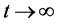 ,其中
,其中 为方程(18)任意解。
为方程(18)任意解。
即存在整数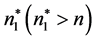 使得所有
使得所有 ,
,

从系统(1)的第二和第四个式子,我们得到
 (19)
(19)
那么

其中 。由脉冲的连续性,我们得频闪映射
。由脉冲的连续性,我们得频闪映射

其中 。
。
由条件 得
得 ,有
,有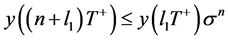 所以当
所以当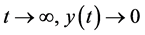 。因此存在一个充分小的
。因此存在一个充分小的 ,使得对所有的
,使得对所有的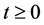 有
有 。
。
由系统(1),得到
 (20)
(20)
类似的,用比较原理和引理2.1,存在一个充分小的 且存在
且存在 使得
使得
 (21)
(21)
其中
同理我们可以得到
 (22)
(22)
类似的,存在一个充分小的 且存在
且存在 使得
使得
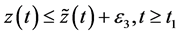
其中

不难得到当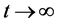 时,有
时,有 和
和 。证毕。
。证毕。
基金项目
国家自然科学基金(11471061);重庆市自然科学基金(No. CQ CSTC 2014JCYJA4004);重庆市高校创新团队计划(No. KJTD201308)。
文章引用
王娜,杨志春. 一类具有周期系数的脉冲种群模型稳定性分析
Stability Analysis of an Impulsively Population Control Model in Periodical Environment[J]. 应用数学进展, 2016, 05(01): 15-23. http://dx.doi.org/10.12677/AAM.2016.51003
参考文献 (References)
- 1. Jiao, J.J., Chen, L.S. and Cai, S.H. (2012) Dynamical Analysis of a Biological Resource Management Model with Im-pulsive Releasing and Harvesting. Advances in Difference Equations, 9, 1-15.
- 2. Singh Jatav, K. and Dhar, J. (2013) Hybrid Approach for Pest Control with Impulsive Releasing of Natural Enemies and Chemical Pesticides: A Plant-Pest-Natural Enemy Model. Nonlinear Analysis: Hybrid Systems, 9, 1-14.
- 3. Georgescu, P. and Morosanu, G. (2008) Impulsive Perturbations of a Three-Trophic Prey-Dependent Food Chain System. Mathematical and Computer Modelling, 48, 975-997. http://dx.doi.org/10.1016/j.mcm.2007.12.006
- 4. 杨志春. 具有脉冲和HollingⅢ类功能反应的捕食系统的持续生存和周期解[J]. Journal of Biomathematics, 2004, 19(4): 439-444.
- 5. Liu, X.N. and Chen, L.S. (2004) Global Dynamics of the Periodic System with Periodic Impulsive Perturbations. Journal of Mathe-matical Analysis and Applications, 289, 279-291. http://dx.doi.org/10.1016/j.jmaa.2003.09.058
- 6. Tang, S.Y. and Chen, L.S. (2002) The Periodic Predator-Prey Lokta-Volterra Model with Impulsive Effect. Journal of Mechanics in Medicine and Biology, 2, 267-296. http://dx.doi.org/10.1142/S021951940200040X
- 7. Wang, W.M., Wang, X.Q. and Lin, Y.Z. (2008) Complicated Dynamics of a Predator-Prey System with Watt-Type Functional Response and Impulsive Control Strategy. Chaos Solitons and Fractals, 37, 1427-1441. http://dx.doi.org/10.1016/j.chaos.2006.10.032
- 8. Song, X.Y. and Li, Y.F. (2007) Dynamics Complexities of a HollingⅡ Two-Prey One-Predator System with Impulsive Effect. Chaos Solitons and Fractals, 33, 463-478. http://dx.doi.org/10.1016/j.chaos.2006.01.019
- 9. Liu, K.Y., Meng, X.Z. and Chen, L.S. (2008) A New Stage Structured Predator-Prey Gomportz Model with Time Delay and Impulsive Perturbations on the Prey. Applied Mathe-matics and Computation, 196, 705-719. http://dx.doi.org/10.1016/j.amc.2007.07.020
- 10. Bainov, D. and Simeonov, P. (1993) Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical, England, 39-53.
- 11. 宋新宇, 郭红建, 师向云. 脉冲微分方程理论及其应用[M]. 北京: 科学出版社, 2011: 19-23, 98-109.