Advances in Applied Mathematics
Vol.06 No.01(2017), Article ID:19532,9
pages
10.12677/AAM.2017.61003
Limit Cycles for a Class of Discontinuous Generalized Lienard Differential Systems
Cuilian Yu
College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua Zhejiang

Received: Dec. 21st, 2016; accepted: Jan. 9th, 2017; published: Jan. 16th, 2017
Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
By using the Melnikov function theory, we study the maximum number of limit cycles which bifurcate from the periodic annulus of the nonlinear center for a class of generalized Lienard differential systems. By piecewise smooth polynomial perturbating, the estimation of the maximum number of limit cycles which bifurcate from the periodic annulus of this nonlinear center is obtained.
Keywords:Limit Cycles, Melnikov Functions, Piecewise Systems, Nonlinear Center

一类不连续广义Lienard微分系统的极限环
余翠连
浙江师范大学,数理与信息工程学院,浙江 金华

收稿日期:2016年12月21日;录用日期:2017年1月9日;发布日期:2017年1月16日

摘 要
利用Melnikov函数方法,我们研究从一类不连续广义Lienard微分系统的非线性中心的周期环域分支出极限环的最大个数问题。通过对该系统的非线性中心进行分段光滑的多项式扰动,得到了该系统从非线性中心的周期环域分支出极限环最大个数的估计。
关键词 :极限环,Melnikov函数,不连续系统,非线性中心

1. 引言
众所周知,希尔伯特第16问题就是考虑平面多项式微分系统的极限环个数问题。但是对于一般的多项式微分系统,研究该问题是非常困难的,所以人们考虑了一些特殊的系统。比如Lienard微分系统
 (1)
(1)
系统(1)的极限环个数问题一直被不断地研究,并且得到了许多经典的结果,如文献 [1] [2] [3] 。
在文献 [4] 中,作者把Lienard微分系统进行进一步推广,研究了下面广义Lienard微分系统
 (2)
(2)
其中 ,
, 是正整数,
是正整数, 是m次多项式,文章证明了从该系统非线性中心的周期环域最多分支出
是m次多项式,文章证明了从该系统非线性中心的周期环域最多分支出 个极限环。
个极限环。
然而,随着现实生活中出现许多不连续现象,越来越多的数学工作者开始研究不连续Lienard微分系统的分支问题。 例如文献 [5] 考虑了下面不连续Lienard微分系统
 (3)
(3)
其中 ,
,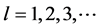 。运用不连续微分系统的一阶平均法,得到了该系统(3)
。运用不连续微分系统的一阶平均法,得到了该系统(3)
从中心的周期环域分支出极限环最大个数的线性估计。关于不连续微分系统更多的研究可见文献 [6] [7] 。
鉴于不连续微分系统的重要性,本文讨论如下类型的不连续广义Lienard微分系统
 (4)
(4)
其中
 ,
, ,
, (5)
(5)
 为正整数且
为正整数且 。
。
利用文献 [8] 中介绍的Melnikov函数方法,本文考虑了系统(4)从非线性中心的周期环域分支出极限环的最大个数问题。我们的主要结果如下:
定理1.1 假设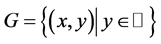 ,
, 为系统(4)从非线性中心
为系统(4)从非线性中心 ,
, 的周期环域分
的周期环域分
支出来的极限环的最大个数。
(i) 若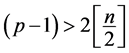 ,则
,则
(ii) 若 ,则
,则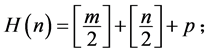
(iii) 若 ,则
,则
注:当 、
、 、
、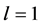 时,文献 [9] 同样运用Melnikov函数证明了该不连续微分系统从线性中心
时,文献 [9] 同样运用Melnikov函数证明了该不连续微分系统从线性中心
的周期环域可以分支出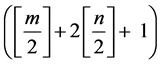 个极限环。显然,文献 [9] 的结果是定理1.1的结论(iii)的一种情
个极限环。显然,文献 [9] 的结果是定理1.1的结论(iii)的一种情
形。结果表明:在非线性中心的扰动下产生的极限环个数总是大于等于在线性中心扰动下的极限环个数,且极限环的个数与y的系数 是无关的。
是无关的。
2. 预备知识
在这一部分,我们将介绍定理1.1证明过程所运用的Melnikov函数。考虑平面分段近Hamilton系统
 (6)
(6)
其中 ,且
,且 可以表示成下面的形式
可以表示成下面的形式

对系统(6)作以下假设:
(H1) 存在区间 ,系统(6)
,系统(6) 有一族顺时针周期轨道
有一族顺时针周期轨道

(H2) 各周期轨道交轴于不同的两点 和
和 ,这里
,这里 ,且
,且 和
和
在假设(H1)和(H2)下,那么,由文献 [8] 中的定理1.1 和文献 [10] 中的引理2.2,可以得到系统(6)的Melnikov函数为
 (7)
(7)
这里 和
和 表示
表示 和
和 .此时,确定系统(6)的极限环个数问题就转化为求一阶Melnikov函数孤立零点个数(重根按重数计算)的问题。由文献 [11] 等式(7)等价于
.此时,确定系统(6)的极限环个数问题就转化为求一阶Melnikov函数孤立零点个数(重根按重数计算)的问题。由文献 [11] 等式(7)等价于
 (8)
(8)
其中
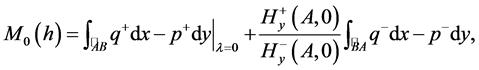

此时,对于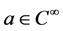 ,函数
,函数 满足
满足
 (9)
(9)
从文献 [11] 可知,若 在区间
在区间 有k个零点,则系统(6)从周期环域分支出k个极限环。所以只要考虑在(8)中第一个非零
有k个零点,则系统(6)从周期环域分支出k个极限环。所以只要考虑在(8)中第一个非零 的零点个数就能够得到
的零点个数就能够得到 的零点个数。
的零点个数。
在证明定理1.1之前,先给出一个在文献 [12] 的引理:
引理1.1如果函数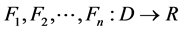 在实数R上是线性无关的,那么存在
在实数R上是线性无关的,那么存在 和
和 ,有
,有

3. 定理1.1的证明
为了运用函数(8),我们令 。为了方便运算,再把
。为了方便运算,再把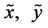 用x,y表示,则系统(4)等价于
用x,y表示,则系统(4)等价于
 (10)
(10)
根据(8)式,系统(10)的一阶Melnikov函数为

其中
 (11)
(11)
这里
 (12)
(12)
易知系统(10)是分段近Hamilton系统,且它的Hamilton函数为
 ,
,
并且当 时,系统(10)有一族周期轨道
时,系统(10)有一族周期轨道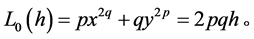 在证明定理1.1过程中,我们得到以下引理:
在证明定理1.1过程中,我们得到以下引理:
引理3.1 如果函数 则
则 至多存在
至多存在 个孤立的正零点。对于一些多项式
个孤立的正零点。对于一些多项式 和
和 ,这零点的最大个数是可以取得的。且当多项式
,这零点的最大个数是可以取得的。且当多项式 和
和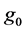 是奇函数时,函数
是奇函数时,函数 恒等于零。
恒等于零。
证明:根据(5),(10),(12)和格林公式,有
 (13)
(13)
通过运用格林公式和一般的Liapunov极坐标变换 (三角函数
(三角函数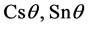 的详细介绍可见文献 [13] ),则
的详细介绍可见文献 [13] ),则 可变为
可变为
 (14)
(14)
从文献 [13] 可知
 (15)
(15)
又根据(13)得
 (16)
(16)
令 ,把(15)代入(14),再把(14),(16)代入(13),有
,把(15)代入(14),再把(14),(16)代入(13),有
 (17)
(17)
在系统(4)中,可知p,q满足 ,则(17)等价于
,则(17)等价于
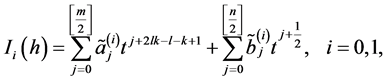 (18)
(18)
其中
 (19)
(19)
特别地,对于 ,从上面分析可知
,从上面分析可知 . 根据(18)式,我们可以知道函数
. 根据(18)式,我们可以知道函数 至多有
至多有 个孤立的正零点。显然
个孤立的正零点。显然 是独立的,所以函数
是独立的,所以函数 孤立零点的最大个数是可以
孤立零点的最大个数是可以
得到的。同时根据(18),(19)式也可以得到引理3.2。
引理3.2 假设 是阶数分别为m,n的奇函数,那么函数
是阶数分别为m,n的奇函数,那么函数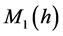 至多存在孤立的正零点个数
至多存在孤立的正零点个数 为
为
(i) 若 ,则
,则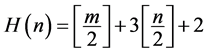 ;
;
(ii) 若 ,则
,则 ;
;
(iii) 若 ,则
,则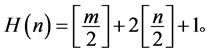
证明:其中沿着周期轨道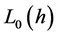 ,我们有
,我们有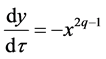 ,则由(12)得
,则由(12)得
 (20)
(20)
因为 是奇函数,则可得
是奇函数,则可得

根据等式(12)得
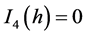 (21)
(21)
由上述预备知识可知 和
和 是满足下列方程的两个解
是满足下列方程的两个解
 (22)
(22)
方程(22)两边对 求导得
求导得
 (23)
(23)
则
 (24)
(24)
根据(11),(18)得
 (25)
(25)
因为 是奇函数,所以
是奇函数,所以 可以表示成
可以表示成
 (26)
(26)
根据前面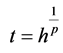 ,则从(5),(9),(13),(25)和(26)式可知
,则从(5),(9),(13),(25)和(26)式可知
 (27)
(27)
其中

综合上述(11),(18),(20),(27)式,则函数 的表达式为
的表达式为

其中

函数 的零点等价于
的零点等价于 的零点,且
的零点,且
 (28)
(28)
为了计算函数 的零点,我们按下面的情况进行分类讨论:
的零点,我们按下面的情况进行分类讨论:
第一种情况:假设 ,此时在(28)式中任意参数
,此时在(28)式中任意参数 是独立的,因此,根据预备知识中的引理1.1,我们可以知道函数
是独立的,因此,根据预备知识中的引理1.1,我们可以知道函数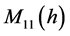 至多存在
至多存在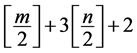 个零点。
个零点。
第二种情况:假设 ,在这种情况下,函数
,在这种情况下,函数 的表达式可写成
的表达式可写成
 (29)
(29)
其中

我们注意到对任意参数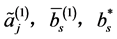 是独立的,从引理1.1我们可知函数
是独立的,从引理1.1我们可知函数 至多可存在
至多可存在 个零点。
个零点。
第三种情况:假设 ,这时函数
,这时函数 的表达式是
的表达式是
 (30)
(30)
其中

容易证明对任意参数 是独立的,因此,根据引理1,函数
是独立的,因此,根据引理1,函数 至多可存在
至多可存在 个零点。
个零点。
综合上述三种情况,引理3.2证毕。
根据引理3.1,假设 ,如果
,如果 不恒等于0,那么函数
不恒等于0,那么函数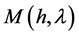 的零点的最大个数在引理3可以得到,则定理1.1已经得证。
的零点的最大个数在引理3可以得到,则定理1.1已经得证。
4. 结束语
经过计算和证明,我们得到了该系统从非线性中心的周期环域分支出极限环最大个数的估计。结果表明:在非线性中心的扰动下产生的极限环个数总是大于等于在线性中心扰动下的极限环个数,且极限环的个数与y的指数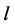 是无关的。
是无关的。
致谢
在论文写作过程中得了老师和同学的帮助和指导,在此表示感谢。同时我也要感谢学校和学校的领导给我们创造的良好的学习环境,让我们能够在良好的氛围中完成论文。最后,感谢国家自然科学基金(11171309, 11172269)的支持。
基金项目
国家自然科学基金(11171309, 11172269)。
文章引用
余翠连. 一类不连续广义Lienard微分系统的极限环
Limit Cycles for a Class of Discontinuous Generalized Lienard Differential Systems[J]. 应用数学进展, 2017, 06(01): 20-28. http://dx.doi.org/10.12677/AAM.2017.61003
参考文献 (References)
- 1. Maesschalck, P.D. and Dumortier, F. (2011) Classical Lienard Equations of Degree n ≥ 6 Can Have [(n − 1) = 2] + 2 Limit Cycles. Journal of Differential Equations, 250, 2162-2176.
- 2. Caubergh, M. and Dumortier, F. (2008) Hilbert’s 16th Problem for Classical Lienard Equations of Even Degree. Journal of Differential Equations, 244, 1359-1394.
- 3. Li, C. and Llibre, J. (2012) Uniqueness of Limit cycles for Lienard Differential Equations of Degree Four. Journal of Differential Equations, 252, 3142-3162.
- 4. Llibre, J. and Makhlouf, A. (2015) Limit Cycles of a Class of Generalized Lienard Polynomial Equations. Journal of Dynamical and Control Systems, 12, 189-192. https://doi.org/10.1007/s10883-014-9253-4
- 5. 李时敏. 一类不连续广义Lienard微分系统的极限环分支[J]. 中山大学学报(自然科学版), 2015, 54(5): 16-18.
- 6. di Bernardo, M., Budd, C.J., Champneys, A.R. and Kowalczyk, P. (2008) Piecewise-Smooth Dynamical Systems Theory and Applications. Springer-Verlag, London.
- 7. Li, S.M. and Liu, C.J. (2015) A Linear Estimate of the Number of Limit Cycles for Some Planar Piecewise Smooth Quadratic Differential System. Journal of Mathematical Analysis and Applications, 428, 1354-1367.
- 8. Liu, X. and Han, M. (2010) Bifurcation of Limit Cycles by Perturbing Piecewise Hamiltonian Systems. International Journal of Bifurcation and Chaos, 20, 1379-1390.
- 9. Sheng, L.J. (2016) Limit Cycles of a Class of Piecewise Smooth Lienard Systems. International Journal of Bifurcation and Chaos, 26, 1650009.
- 10. Liang, F. and Han, M. (2012) Limit Cycles Near Generalized Homoclinic and Double Homoclinic Loops in Piece-wise Smooth Systems. Chaos Solitons Fractals, 45, 454-464.
- 11. Xiong, Y. (2015) Limit Cycle Bifurcations by Perturbing Piecewise Smooth Hamitonian Systems with Multiple Parameters. Journal of Mathematical Analysis and Applications, 421, 260-275.
- 12. Llibre, J. and Swirszca, G. (2011) On the Limit Cycles of Polynomial Vector Fields. Dynamics of Continuous Dis-crete & Impulsive Systems, 18, 203-214.
- 13. Liapunov, A.M. (1966) Stability of Motion. With a Contribution by V. A. Pliss Andan Introduction by V. P. Basov. Mathematics in Science and Engineering. Academic Press, New York.