ABSTRACT

Solving the systems of linear equations plays an important role in higher algebra and linear algebra. Cramer rule uses determinant to characterize the existence and uniqueness of solutions of systems of linear equations, which can be applied to the systems of linear equations containing the same number of linear equations and unknown variables, and it is of remarkable theoretic value. In this paper, we will present an alternative proof for Cramer rule by using the properties of determinant, and the inverse proposition of Cramer rule is also proved to be true.

Keywords:System of Linear Equations, Cramer Rule, The Inverse Proposition of Cramer Rule, The Properties of Determinant

一个关于克拉默法则及其逆命题的注记

杜志斌

肇庆学院数学与统计学院，广东 肇庆

收稿日期：2017年2月26日；录用日期：2017年3月18日；发布日期：2017年3月21日

摘 要

解线性方程组是高等代数和线性代数中的一个重要内容。克拉默(Cramer)法则运用了行列式来刻画线性方程组解的存在性和唯一性，它适用于方程个数与未知量个数相等的线性方程组，具有显著的理论价值。本文将利用行列式的性质给出克拉默法则的另一种证明，并证明克拉默法则的逆命题也是正确的。

关键词 :线性方程组，克拉默(Cramer)法则，克拉默(Cramer)法则的逆命题，行列式性质

Copyright © 2017 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

线性方程是指未知量均为一次的方程，多个线性方程可组成线性方程组，比如说，

(1)

为一个含有个未知量，条线性方程的线性方程组。

关于线性方程组的研究最早可追溯到公元一世纪初的《九章算术》方程章。事实上，现今大量科学技术问题可归结为解线性方程组。因此，线性方程组在多个学科和领域中皆有着重要应用，如数学、工程学、经济学等。

作为线性方程组研究中最基本且最重要的研究内容，线性方程组解的存在性与唯一性一直都是线性方程组的研究核心。特别地，对于方程个数与未知量个数相等的线性方程组，克拉默(Cramer)法则运用行列式来刻画此类线性方程组的系数与解的存在性和唯一性之间的关系，见 [1] [2] 。

记

为线性方程组(1)的系数行列式，且记

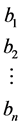
为线性方程组(1)的常数项。此外，对任意，记为将系数行列式的第列换成常数项后所得的行列式，即

定理1 (克拉默法则) 若线性方程组(1)的系数行列式，则该线性方程组具有唯一解，且该唯一解为

根据线性方程组有唯一解的判别法(见 [1] [2] )，易知克拉默法则的逆命题也是正确的。

定理2 (克拉默法则的逆命题)若线性方程组(1)具有唯一解，则其系数行列式。

在高等代数和线性代数的教材中，克拉默法则常常作为行列式的应用出现。学者们一般采用行列式按行(列)展开的公式来证明克拉默法则，但证明过程中牵涉到多个连和式子，略显繁琐，如 [1] [2] ，或者干脆暂且不证明，等到后面讲述完逆矩阵与伴随矩阵的关系之后，再补充证明，如 [3] [4] [5] [6] 。此外，教材在讲述克拉默法则时，极少提及到克拉默法则的逆命题也是正确的。

为了教学上的连贯性以及证明的易读性，我们有必要引入一种仅与行列式的定义和性质有关，且简单明了的方法来证明克拉默法则及其逆命题。本文将以此为主旨，运用行列式的性质来证明克拉默法则(即定理1)，以及证明克拉默法则的逆命题(即定理2)也是正确的。

2. 克拉默法则的基于行列式性质的证明方法

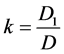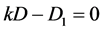定理1的证明首先证明线性方程组(1)的解的存在性。令，等价地，，即

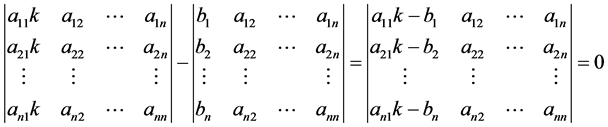
这表明行列式

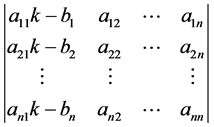
中存在某一列可由其余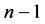列线性表示，更一般地，可知存在不全为0的常数，使得

(2)

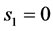首先假设，则有

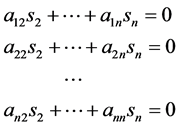
于是，系数行列式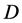中存在某一列可由其余列线性表示，可得，这与假设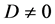矛盾。因此，。

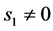现对方程组(2)移项后，可得

于是，

为线性方程组(1)的一组解，这就证明了线性方程组(1)的解的存在性。

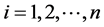接下来证明线性方程组(1)的解的唯一性。设为线性方程组(1)的一组解。对任意，将线性方程组(1)相应地移项后，可得

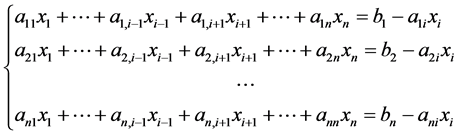
这表明

此外，注意到

进而有，等价地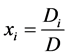，。由此，线性方程组(1)的解的唯一性得证，且该唯一解为

现定理1得证。

3. 克拉默法则的逆命题的基于行列式性质的证明方法

定理2的证明运用反证法，假设，且为线性方程组(1)的唯一解。

首先假设，则线性方程组(1)即为齐次线性方程组

(3)

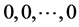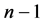一方面，显然是线性方程组(3)的一组解。另一方面，既然，所以系数行列式中存在某一列可由其余列线性表示，不妨假设系数行列式的第列可由其余列线性表示，即存在常数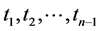，使得

移项后，可得

因此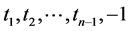，也是线性方程组(3)的一组解，这与线性方程组(3)的解的唯一性矛盾。

再假设不全为0，即线性方程组(1)为非齐次线性方程组。基于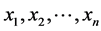为非齐次线性方程组(1)的一组解，以及为齐次线性方程组(3)的一组解，可得知亦为非齐次线性方程组(1)的一组解，这与线性方程组(1)的解的唯一性矛盾。

综上所述，可知。

基金项目

广东省自然科学基金项目(2014A030310277)；广东省教育厅青年创新人才项目(2014KQNCX224)；广东省高等学校优秀青年教师培养计划资助项目。

文章引用

杜志斌. 一个关于克拉默法则及其逆命题的注记
A Remark on the Cramer Rule and Its Inverse Proposition[J]. 应用数学进展, 2017, 06(02): 127-132. http://dx.doi.org/10.12677/AAM.2017.62014

参考文献 (References)