Advances in Applied Mathematics
Vol.06 No.05(2017), Article ID:21684,7
pages
10.12677/AAM.2017.65079
The Largest Existentially Definable Interval of a Class of Second Order Singular Differential Equations
Xiaoling Hu
Guangzhou University, Guangzhou Guangdong

Received: Jul. 21st, 2017; accepted: Aug. 7th, 2017; published: Aug. 14th, 2017

ABSTRACT
In this thesis, we investigate the largest existentially definable interval for the solutions of a class of second order singular differential equations. In the first part, we show the meaning for studying the existence of solutions of ordinary differential equations, some important existence theorems and the largest existentially definable interval theorems for solutions. In the second part, we study the largest existentially definable interval of a class of second order singular differential equations.
Keywords:Ordinary Differential Equations, Differential Equations with Singularities, The Largest Existentially Definable Interval
一类二阶奇异微分方程解的最大存在区间
胡小玲
广州大学,广东 广州
收稿日期:2017年7月21日;录用日期:2017年8月7日;发布日期:2017年8月14日

摘 要
本论文研究一类二阶奇异微分方程解的最大存在区间问题。第一部分我们叙述了研究常微分方程解的存在性的意义,一些重要的常微分方程解的存在定理以及解的最大存在区间定理。第二部分我们研究了一类二阶奇异微分方程的解的最大存在区间。
关键词 :常微分方程,二阶奇异微分方程,最大存在区间

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
常微分方程发展至今已经有了很悠久的历史,并且依然保持着进一步发展的趋势,其中最根本的原因是它与各种实际现实问题息息相关。常微分方程的发展阶段按照研究内容来分,大致可以分为以下几个阶段,即常微分方程经典阶段,常微分方程适定性理论阶段,常微分方程解析理论阶段,常微分方程定性理论阶段,详情请见参考文献 [1] 和文献 [2] 。18世纪及其以前为常微分方程发展的经典阶段,这个阶段的主要研究内容是求通解。19世纪初期和中期为常微分方程发展的适定性理论阶段,以定解问题的适定性理论为其主要研究内容。19世纪末期及20世纪初期为常微分方程发展的解析理论阶段,主要研究内容是求微分方程的解析理论。20世纪中期以后为常微分方程发展的定性理论阶段,主要研究内容是定性与稳定性理论。在本世纪初期,Birkhoff独创了拓扑动力系统以及各态历经的相关理论,至此把常微分方程的研究应用提升到了更高的水平。
随着科学技术的迅速发展,在经济学,生物学,工程学,物理学,化学等很多领域中出现了非常多类型的非线性问题,而流体力学、气体动力学、边界层理论等中的许多非线性问题,又可以用奇异微分方程来概括描述。基于奇异微分方程的深刻的数学意义和广泛的应用背景,许多学者对它的理论研究非常关注,具体可参见文献 [3] [4] [5] [6] [7] [8] 。白阿拉坦高娃 [3] 利用混合有限元的方法对奇异两点边值问题以及一维奇异抛物型方程进行了研究,刘小林 [9] 对一类奇异微分方程与一类全非线性奇异椭圆方程的正则性问题进行了研究,蒋继强 [10] 对整数阶和分数阶上几类微分方程奇异和半正边值问题解的存在性、多解性进行了研究。
常微分方程最重要的理论基础是解的存在性、解的唯一性,即解在什么条件下是存在的,存在区间是多少等。关于常微分方程的解是否存在的问题,一些特殊方程是可以用初等积分法来求解,而相当大一部分方程由初等积分法无法求解,那么就需要借助一些定理来判定该微分方程是否有解,什么条件下有解,通过判定该方程有解,再来讨论方程的解存在区间,最大存在区间问题。本文将对一类二阶奇异微分方程的解的最大存在区间进行讨论。
2. 常微分方程解的存在性及解的最大存在区间
2.1. 常微分方程解的存在性
随着微分方程在实际问题中的应用越来越广泛,求得微分方程的解也对于我们处理实际问题提供了非常重要的帮助。我们已经知道一些特殊方程的求解问题,例如用一阶微分方程的初等积分法来求解,
但是,对于许多的方程不能用初等积分法求解,比如Riccati方程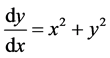 ,那么这类不能用初等积分
,那么这类不能用初等积分
法来求解的常微分方程在什么条件下一定会有解呢?下面是判断一些常微分方程有解的重要定理 [11] [12] 。
1) Lipschitz条件
设函数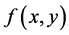 在某一区域D里满足以下不等式
在某一区域D里满足以下不等式
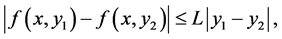
其中常数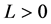 。那么就称函数
。那么就称函数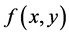 在这个区域D里面对
在这个区域D里面对 满足Lipschitz条件。
满足Lipschitz条件。
2) Picard定理
对于初值问题
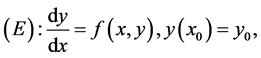
其中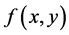 在以下矩形区域
在以下矩形区域
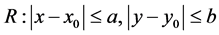
内连续,并且对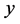 满足Lipschitz条件。那么
满足Lipschitz条件。那么 在
在 的这个区间上有且只有一个解,其中常数
的这个区间上有且只有一个解,其中常数
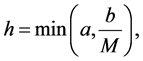 而
而
3) Peano存在定理
令函数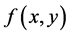 在上面所提及到的矩形区域R里面连续,那么初值问题
在上面所提及到的矩形区域R里面连续,那么初值问题
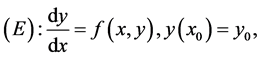
在 的这个区间上最少有一个解
的这个区间上最少有一个解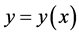 ,h的定义同上。
,h的定义同上。
2.2. 常微分方程解的最大存在区间
上面的定理表示我们只满足于在局部范围内讨论初值问题解的存在性,现在把这种讨论扩大到整体,讨论常微分方程解的最大存在区间。以下是关于解的存在区间的一些重要定理 [13] [14] 。
1) 解的延伸定理
令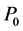 是任意区域
是任意区域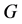 里的任一点,并且设
里的任一点,并且设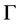 为微分方程
为微分方程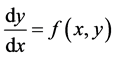 经过
经过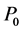 点的任意的一条积分曲线。
点的任意的一条积分曲线。
那么积分曲线 将会在任意区域
将会在任意区域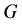 内延伸至边界,也就是说,对任意的有界区域
内延伸至边界,也就是说,对任意的有界区域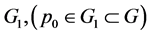 ,那么积分曲线
,那么积分曲线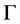 将会延伸至
将会延伸至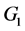 的外面。
的外面。
2) 解的最大存在区间定理
设微分方程
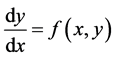
其中函数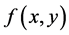 在下面条形区域
在下面条形区域
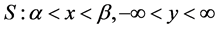
里面连续,且满足下面的不等式

其中 与
与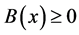 在
在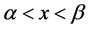 上连续。那么微分方程
上连续。那么微分方程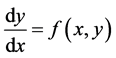 的任何一个解都以
的任何一个解都以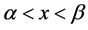 这
这
个区间为最大存在区间。
3) 第一比较定理
设函数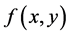 和
和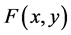 都在平面区域
都在平面区域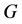 里面连续而且还满足以下不等式
里面连续而且还满足以下不等式

又设函数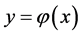 和
和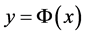 在
在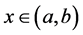 上依次是初值问题
上依次是初值问题
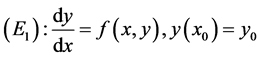
和
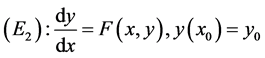
的解,其中 。那么我们有
。那么我们有
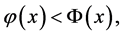 当
当
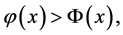 当
当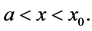
3. 一类二阶奇异微分方程解的最大存在区间
基于解的最大存在区间在各类微分方程研究中的重要性,近年来,这一问题越来越多地受到一些学者的强烈关注。本文讨论一类二阶奇异微分方程
 (3.1)
(3.1)
其中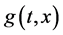 是连续且满足
是连续且满足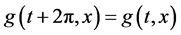 ,同时满足局部Lipschitz条件,而且在原点处有奇异性,即
,同时满足局部Lipschitz条件,而且在原点处有奇异性,即 ;
; 是以
是以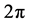 为周期的连续函数。为研究方便,我们将原点处的奇异性平移,也就是
为周期的连续函数。为研究方便,我们将原点处的奇异性平移,也就是
说令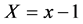 。原方程(3.1)可化为
。原方程(3.1)可化为
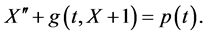
记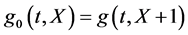 ,则
,则
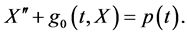
为方便计,我们仍考虑方程
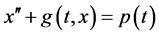 (3.2)
(3.2)
其中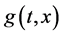 是连续且满足
是连续且满足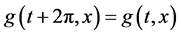 ,同时满足局部Lipschitz条件,而且在
,同时满足局部Lipschitz条件,而且在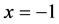 点处有奇异性,即
点处有奇异性,即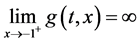 ;
;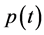 是以
是以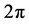 为周期的连续函数。令
为周期的连续函数。令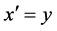 ,则(3.2)可化为
,则(3.2)可化为
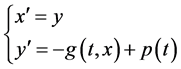 (3.3)
(3.3)
给定初始值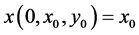 ,
,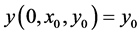 ,那么有
,那么有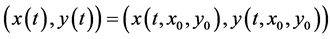 为方程(3.2)的解。下面考虑(3.2)的解的最大存在区间。
为方程(3.2)的解。下面考虑(3.2)的解的最大存在区间。
定理3.1 假设存在连续函数 ,
,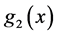 ,使
,使
 ,对
,对 一致成立
一致成立 
同时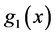 ,
,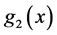 满足
满足
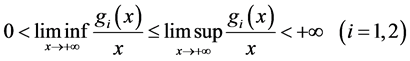
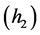
与
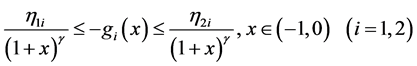
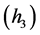
其中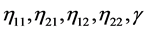 都是正常数。则对于系统(3.3)的任何一个解
都是正常数。则对于系统(3.3)的任何一个解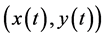 ,其最大存在区间为
,其最大存在区间为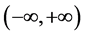 。
。
证明:定义一个势函数
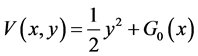 ,
,
其中 。
。
令
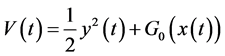
因此我们有

由于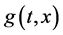 是以
是以 为周期的连续函数,所以存在连续函数
为周期的连续函数,所以存在连续函数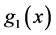 和
和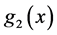 满足
满足
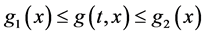
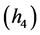
其中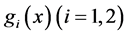 满足式
满足式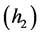 和
和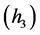 。
。
类似于文献 [4] 和文献 [5] 的方法,从式 和
和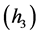 我们可知,存在一个常数
我们可知,存在一个常数 使得
使得
 ,
,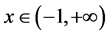
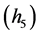
其中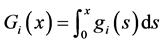 ,
,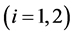
令 ,
,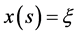 ,则有
,则有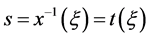 。
。
当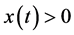 时,有
时,有
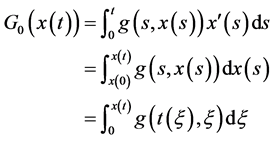
由式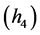 有
有
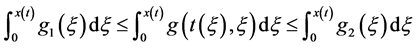
成立。
当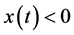 时,有
时,有
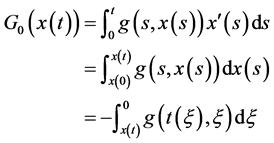
由式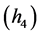 有
有
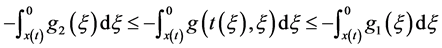
成立。
又由式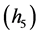 ,所以必存在
,所以必存在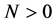 满足
满足
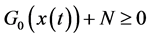 ,
, 
其中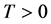 。
。
因此,
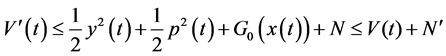
其中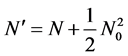 ,
,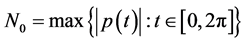 。那么对任意有限的
。那么对任意有限的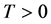 ,我们有
,我们有
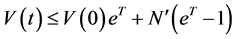 ,
, 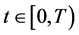
因此,在任何有限的区间 上不存在突变点
上不存在突变点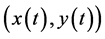 。所以,解
。所以,解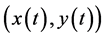 在区间
在区间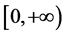 上存在。同理,我们也可以证明解
上存在。同理,我们也可以证明解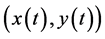 在区间
在区间 上存在。由于
上存在。由于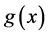 满足局部Lipschitz条件,解
满足局部Lipschitz条件,解 是存在唯一的,因此,方程(3.2)的解的最大存在区间为
是存在唯一的,因此,方程(3.2)的解的最大存在区间为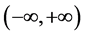 。
。
4. 总结
本文讨论了一类具体的二阶奇异微分方程的解的最大存在区间问题,由定理3.1及其证明,给出了这类解的最大存在区间为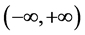 。由于解的最大存在区间在各类微分方程研究中的重要性,还有很多问题值得讨论,例如,更多微分方程的解的最大存在区间如何确定,是否存在一种方法适用于确定大部分微分方程的解的最大存在区间问题等。
。由于解的最大存在区间在各类微分方程研究中的重要性,还有很多问题值得讨论,例如,更多微分方程的解的最大存在区间如何确定,是否存在一种方法适用于确定大部分微分方程的解的最大存在区间问题等。
文章引用
胡小玲. 一类二阶奇异微分方程解的最大存在区间
The Largest Existentially Definable Interval of a Class of Second Order Singular Differential Equations[J]. 应用数学进展, 2017, 06(05): 670-676. http://dx.doi.org/10.12677/AAM.2017.65079
参考文献 (References)
- 1. 李文林. 数学史教程[M]. 北京: 高等教育出版社, 2004: 3-14.
- 2. 王树禾. 数学思想史[M]. 北京: 国防工业出版社, 2003: 2-23.
- 3. 白阿拉坦高娃. 一维奇异微分方程的混合有限元方法[D]: [硕士学位论文]. 呼和浩特: 内蒙古大学, 2011.
- 4. Wang, Z. and Ma, T. (2012) Existence and Multiplicity of Periodic Solutions of Semilinear Resonant Duffing Equations with Singularities. Nonlinearity, 25, 279. https://doi.org/10.1088/0951-7715/25/2/279
- 5. Wang, Z. (2014) Lazer-Leach Type Conditions on Periodic Solutions of Semilinear Resonant Duffing Equations with Singularities. Zeitschrift Für Angewandte Mathematik Und Physik, 65, 69-89. https://doi.org/10.1007/s00033-013-0323-3
- 6. Jiang, W., Huang, X., Guo, W., et al. (2013) The Existence of Positive Solutions for the Singular Fractional Differential Equation. Journal of Applied Mathematics & Computing, 41, 171-182. https://doi.org/10.1007/s12190-012-0603-7
- 7. Vong, S.W. (2013) Positive Solutions of Singular Fractional Differential Equ-ations with Integral Boundary Conditions. Mathematical & Computer Modelling, 57, 1053-1059. https://doi.org/10.1016/j.mcm.2012.06.024
- 8. Han, Z. (2012) Uniqueness of Positive Solutions for Boundary Value Problems of Singular Fractional Differential Equations. Inverse Problems in Science & Engineering, 20, 299-309. https://doi.org/10.1080/17415977.2011.603726
- 9. 刘小林. 一类奇异微分方程解的正则性及其应用[D]: [博士学位论文]. 北京: 清华大学, 2013.
- 10. 蒋继强. 非线性奇异微分方程边值问题的正解及其应用[D]: [博士学位论文]. 曲阜: 曲阜师范大学, 2013.
- 11. 丁同仁, 李承治. 常微分方程教程[M]. 北京: 高等教育出版社, 1991: 7-23.
- 12. 丁同仁. 常微分方程定性方法的应用[M]. 北京: 高等教育出版社, 2004: 8-31.
- 13. 弭鲁芳, 纪在秀. 论一类常微分方程解的最大存在区间[J]. 聊城大学学报, 2006, 19(4): 24-26.
- 14. 孔志宏, 米芳. 微分方程解的存在区间的确定[J]. 大学数学, 2013, 29(5): 71-80.