Advances in Applied Mathematics
Vol.06 No.06(2017), Article ID:22113,12
pages
10.12677/AAM.2017.66089
Subcritical Hopf Bifurcation of a Hematopological System
Suqi Ma
Mathematical Department of Chinese Agricultural University, Beijing

Received: Sep. 1st, 2017; accepted: Sep. 15th, 2017; published: Sep. 21st, 2017

ABSTRACT
The periodic cyclical neutrophil oscillating model of hematopoietic is discussed. Mathematically, the model is a multi-delay DDEs with high nonlinearity. Varying time delay brings forth Hopf bifurcation in system dynamic behavior. By calculating coefficients of normal form, it is analyzed that Hopf bifurcation is sub-critical. Numerical simulation coincides with the theoretical analyze result.
Keywords:Hematological Cell Model, Subcritical Hopf Bifurcation, Delay
造血系统的下临界Hopf分岔
马苏奇
中国农业大学数学系,北京
收稿日期:2017年9月1日;录用日期:2017年9月15日;发布日期:2017年9月21日

摘 要
本文讨论了造血干细胞引发周期噬中性粒子血液病的两房模型。数学上,该模型是一多时滞的时滞微分系统的复杂非线性模型。变化时滞可带来系统的Hopf分岔行为,通过计算范式,分析得出该分岔点处发生了下临界Hopf分岔。数值模拟与理论分析结果一致。
关键词 :造血系统,下临界Hopf分岔,时滞

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在系统生态学动力学行为研究中,造血干细胞模型一直是人们非常关注的一个话题。在数学上,人们致力于应用不同的数学模型来描述干细胞增殖分化的时空动力系统。造血干细胞经分化得到人类必须的三类血液细胞:白细胞、红细胞和血小板。造血功能失调会带来多种血液学疾病,典型的例子有长期发烧、“打摆子”,和慢性的嗜中性粒子白血球减小症。病人呈现出周期性的嗜中性粒子低水平振荡现象,振荡周期经生物学实验证实为11天~19天。应用非线性动力学模型来刻画血液细胞的动力学振荡现象可以帮助理解其复杂动力学机制。
近十几年来,Mackey等人给出了建立血液学疾病机理的基本数学框架 [1] - [7] 。从建模起,描述血液学疾病机理的数学模型是一含有多个滞量的时滞微分系统(DDEs)。造血系统由激发分化和增殖的机制以及成熟机制组成,由于细胞的分化和成熟都需要时间,因此在系统中含有多个时滞。一般地,细胞需要经历的成熟期为2到6天,变化不同参数组合,得到振荡的周期解 [8] 。医学上,人们应用集落刺激因子管理嗜中性粒子减少血液病 [3] [4] [5] 。集落刺激因子管理有助于降低血液细胞的程序性凋亡率和增加增殖分化所需时间。国内Lei等人发展了基于集落刺激因子管理嗜中性粒子的血液病振荡数学模型,一般地,他们给出的数学模型如下 [9] [10] ,
(1)
其中Holling函数
可以看出,模型(1)中干细胞以速率
进入其增殖相,并以速率
进入嗜中性粒子房。其它参数的生理学意义如下,
(1) 造血过程由激发分化和成熟机制组成,具体地,造血干细胞经由细胞分裂分化成为全部血液细胞包括白细胞、红细胞和血小板,并能自我更新,
表示凋亡率,增殖相需要的天数是 。
。
(2) 与嗜中性粒细胞不同的是,血液干细胞分化以速率
分化成为其它血液细胞;
(3) 嗜中性粒细胞耦合时滞为
,由两部分和组成,分别是其前驱细胞的增殖相需要的天数
和成熟相需要的天数
。
是增殖速率,
是成熟相中的死亡率。因而,嗜中性粒细胞的组合相中的放大系数为
注意到速率
和成熟时间
依赖于粒细胞集落刺激因子的管理。考虑到粒细胞集落刺激因子在医学上的成功使用,学者们在周期噬中性粒子的演化模型中,在增殖系数中用时滞来减弱系数。其估计的参数值列出如下
,
,
,
,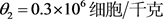 ,
,
,
,
,
,
。选取
和
为分岔参数。文 [11] 分析了系统(1)的长周期解,以及倍周期分岔和多周期解共存等复杂非线性现象,并证实了Haurie生理学实验的结论 [1] [2] [3] [4] [5] ,即造血模型的周期解存在着一个很广泛的周期,例从11天到89天等。
,
,
,
,
,
,
。选取
和
为分岔参数。文 [11] 分析了系统(1)的长周期解,以及倍周期分岔和多周期解共存等复杂非线性现象,并证实了Haurie生理学实验的结论 [1] [2] [3] [4] [5] ,即造血模型的周期解存在着一个很广泛的周期,例从11天到89天等。
本文首先分析了系统的Hopf分岔,其次通过范式分析,证实了Hopf分岔现象是下临界的Hopf分岔现象,并给出了下临界Hopf分岔的数值模拟。
2. Hopf分岔分析
设
是系统(1)的平衡点,计算方程在平衡点的特征值,如果方程(1)的特征方程有一对纯虚根
,并满足横截条件,则方程(1)发生了Hopf分岔,且经由Hopf分岔,系统(1)出现稳定或不稳定的周期解。作坐标平移,系统的三次Taylor截断展开式为
其中
和
我们引入向量
,设参数向量
,那么方程(1)可以写成其向量形式
(2)
其中
,
,
和
(3)
设
表示连续可微函数
构成的巴拿赫空间,定义时间平移
,
,那么方程(2)的算子微分方程形式为
(4)
这里,设在Hopf分岔临界值处的线性算子
为
(5)
非线性算子
可被写作(6)
(6)
其中
。
设连续可微函数
构成空间
,在 上定义线性算子
的伴随线性算子为
上定义线性算子
的伴随线性算子为
定义双线性形式
为
(7)
容易证明,有
成立。
在临界Hopf分岔值
处,有一对纯虚特征值
,且其余特征值都具有负实部。因而
可被分解为
,其中
为相应于
的特征空间,而
是其补空间。计算得
相应于特征值
的特征向量为
,
,
相应于
的特征向量为
,
,满足
,进一步可证明
。
注意到
(8)
每个
可以被写作
(9)
使得
(10)
对(9)两边微分,注意到(8)式成立,因而可得
(11)
其中
(12)
3. 二维中心流形
将
展开成级数
(13)
其中系数
依赖于
,令
,把方程(11)写作
(13)
其中
有展式
(14)
其中
为常数,计算见附录。
从方程(9)和(11)可得
(15)
方程(14)的第一个方程可以写成
(16)
其中
其中系数
。
由于
所以
,
,
,
为了决定分岔解的行为,通过下式计算
。
(17)
注意到算子
的定义,(17)式即
,
(18)
相似地,由方程(15)的第二个方程得到初值条件
(19)
对方程(18)积分在初值条件(19)下积分,可得出
(20.1)
(20.2)
 (20.3)
(20.3)
其中系数
由方程初值条件(19)决定。
4. 下临界Hopf分岔
当特征值穿越虚轴时,系统(1)的平衡点处发生了Hopf分岔,一般的Hopf分岔分为超临界的Hopf分岔和下临界的Hopf分岔。若当参数值小于临界值时分岔出不稳定的周期解,Hopf分岔被称为是下临界的;若当参数值大于临界值时分岔出的周期解是稳定的,Hopf分岔被称为是超临界的。对平衡点作分析,方程(1)的线性化方程的特征方程为
(21)
当有一对共轭复特征值穿越虚轴时,方程(1)的平衡点的稳定性发生改变,这时方程(21)确定了一对

Figure 1. Periodic solutions near the subcritical Hopf point, wherein stable periodic solutions is denoted by blue lines, whilst unstable perioidc solutions represented by red lines
图1. 下临界hopf点附近的周期解。红线表示不稳定周期解,蓝线表示稳定的周期解
Hopf分岔的临界值
。并由方程(21)确定
,即系统在Hopf临界值处满足横截性。
由特征方程(21)可以计算
,以上计算得到大于零的第一Lyapunov数,又由于
,从而Hopf分岔是下临界的。数值模拟得到该Hopf分岔点附近的周期解,如图1所示。
5. 总结
本文应用Hopf分岔原理研究造血系统中噬中性粒子数周期性振荡现象发生的机制。模型中引入集落刺激因子管理,有助于降低血液细胞的程序性凋亡率和增加增殖分化所需时间,在数学上,使得造血系统成为含时滞依赖物理参数的多时滞系统。变化时滞得到系统的Hopf分岔点,应用范式理论进一步得到该分岔是下临界Hopf分岔现象。连续延拓得到系统共存的稳定周期解和不稳定周期解。
文章引用
马苏奇. 造血系统的下临界Hopf分岔
Subcritical Hopf Bifurcation of a Hematopological System[J]. 应用数学进展, 2017, 06(06): 740-751. http://dx.doi.org/10.12677/AAM.2017.66089
参考文献 (References)
- 1. Lei, J.Z. and Mackey, M.C. (2014) Understanding and Treating Cytopenia through Mathematical Modeling. Springer, New York, 844, 279-302. https://doi.org/10.1007/978-1-4939-2095-2_14
- 2. Zhuge, C.J., Lei, J.Z. and Mackey, M.C. (2002) Neutrophil Dynamics in Response to Chemotherapy and G-CSF. Journal of Theoretical Biology, 293,111-120. https://doi.org/10.1016/j.jtbi.2011.10.017
- 3. 马苏奇. 造血系统中的周期解分岔及反馈控制[J]. 应用数学进展, 待发表.
- 4. Mackey, M.C. (1978) Unified Hypothesis for the Aplastic Anemia and Periodic Hematopoiesis. Blood, 51, 941-956.
- 5. Mackey, M.C. (1979) Dynamic Hematopological Disorders of Stem Cell Origin, Biophysical and Biochemical Information Transfer in Rec-ognition. Plenum, New York, 373-409. https://doi.org/10.1007/978-1-4899-5330-8_33
- 6. Haurie, C., Dale, D.C. and Mackey, M.C. (1998) Cyclical Neutropenia and Other Periodic Hematological Diseases: A Review of Mechanisms and Mathematical Models. Blood, 92, 2629-2640.
- 7. Haurie, C., Dale, D.C. and Mackey, M.C. (1999) Occurrence of Periodic Oscillations in the Differential Blood Counts of Congenital, Idiopathic and Cyclical Neutropenic Patients before and during Treatment with G-CSF. Experimental Hematology, 27, 401-409. https://doi.org/10.1016/S0301-472X(98)00061-7
- 8. Haurie, C., Person, R., Hale, D.C. and Mackey, M.C. (1999) Haematopoietic Dynamics in Grey Collies. Experimental Hematology, 27, 1139-1148. https://doi.org/10.1016/S0301-472X(99)00051-X
- 9. Haurie, C., Hale, D.C., Rudnicki, R. and Mackey, M.C. (2000) Modelling Complex Neutrophil Dynamics in the Grey Collie. Journal of Theoretical Biology, 204, 505-519. https://doi.org/10.1006/jtbi.2000.2034
- 10. Hearn, T., Haurie, C. and Mackey, M.C. (1998) Cyclical Neutropenia and Peripheral Control of White Blood Cell Production. Journal of Theoretical Biology, 192,167-181. https://doi.org/10.1006/jtbi.1997.0589
- 11. Bernard, S., Belair, J. and Mackey, M.C. (2003) Oscillations in Cyclical Neutropenia: New Evidence Based on Mathematical Modeling. Journal of Theoretical Biology, 223, 283-298. https://doi.org/10.1016/S0022-5193(03)00090-0
附录
计算
相应于特征值
的特征向量为
,
,
相应于
的特征向量为
,
由定义直接计算得
而且
比较
在方程两边的系数得
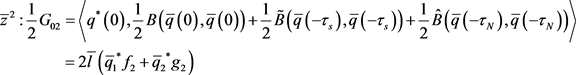
其中,
知网检索的两种方式:
1. 打开知网页面http://kns.cnki.net/kns/brief/result.aspx?dbPrefix=WWJD
下拉列表框选择:[ISSN],输入期刊ISSN:2324-7991,即可查询
2. 打开知网首页http://cnki.net/
左侧“国际文献总库”进入,输入文章标题,即可查询
投稿请点击:http://www.hanspub.org/Submission.aspx
期刊邮箱:aam@hanspub.org






 。
。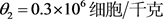 ,
,
,
,
,
,
。选取
和
为分岔参数。文 [11] 分析了系统(1)的长周期解,以及倍周期分岔和多周期解共存等复杂非线性现象,并证实了Haurie生理学实验的结论 [1] [2] [3] [4] [5] ,即造血模型的周期解存在着一个很广泛的周期,例从11天到89天等。
,
,
,
,
,
,
。选取
和
为分岔参数。文 [11] 分析了系统(1)的长周期解,以及倍周期分岔和多周期解共存等复杂非线性现象,并证实了Haurie生理学实验的结论 [1] [2] [3] [4] [5] ,即造血模型的周期解存在着一个很广泛的周期,例从11天到89天等。 上定义线性算子
的伴随线性算子为
上定义线性算子
的伴随线性算子为 (20.3)
(20.3)