有理Bézier曲线及其应用 Rational Bézier Curve and Its Application

doi:10.12677/AAM.2017.68112

Advances in Applied Mathematics
Vol.06 No.08(2017), Article ID:22765,7 pages
10.12677/AAM.2017.68112

Rational Bézier Curve and Its Application

Fang Wang, Genzhu Bai

●Abstract

●Full-Text PDF

●Full-Text HTML

●Full-Text ePUB

●Linked References

●How to Cite this Article

¹Zhejiang Changzheng Vocational & Technical College, Hangzhou Zhejiang

²Inner Mongolia University for the Nationalities, Tongliao Inner Mongolia

Received: Nov. 3^rd, 2017; accepted: Nov. 16^th, 2017; published: Nov. 23^rd, 2017

ABSTRACT

Our study introduces rational Bézier curves to blend the axes of two tubes with non-coplanar axes. Furthermore, our method constructs blended tubes with the same radius but non-coplanar axes. By choosing appropriate weight factors for the corresponding control vertices, we can control the distances between the axes and the control polygons. Our method could be favorable in application.

Keywords:Rational Bézier Curves, Blending, Axes, Tubes

有理Bézier曲线及其应用

王芳¹，白根柱²

¹浙江长征职业技术学院，浙江杭州

²内蒙古民族大学，内蒙古通辽

收稿日期：2017年11月3日；录用日期：2017年11月16日；发布日期：2017年11月23日

摘要

本文利用有理Bézier曲线光滑拼接两个轴线异面圆管道的轴线，进而构造了光滑拼接两个轴线异面的半径相同圆管道，并适当选择对应控制顶点的权因子可调节轴线靠近或远离控制多边形，以利于应用。

关键词 :有理Bézier曲线，光滑拼接，轴线，管道

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

代数曲面拼接问题是计算机几何设计和几何造型的基本问题，有着广泛的应用。二十世纪以来，随着多元样条函数理论的发展，关于显式或参数曲面的理论研究日益完善。但它们在空间曲面设计的应用是有局限性的。二十世纪60年代以来，由Buchberger提出的Groebner基方法以及吴文俊提出的特征列方法，使得交换代数及代数几何中许多结果变成可计算的。于是，关于曲面拼接问题的研究日益活跃，国内国外的学者在用代数曲面构造光滑拼接曲面方面做了大量的研究工作 [1] [2] [3] [4] [5] 。但是，代数曲面拼接时过渡曲面的形状是未知的，与实际曲面设计需求有一定的差距。另外，工业制造中有时因为管道交叉、障碍物阻扰等因素或其他原因，不仅需要考虑过度参数曲面还要对光滑曲面的形状。所以要考虑轴线异面管道拼接的研究是很必要的，其主要的用途在于工业上具有特定工艺功能的制造。

注意到在构造光滑拼接的过渡曲面时，一般都要求待拼接的曲面有交线或管道的轴线相交。对于两个管道的轴线为异面的情形，相应的拼接技术已有成果不多。雷娜 [6] 证明了二轴异面圆管在其任意平面截口处通常不能用三次代数曲面光滑拼接，提出构造轴线与给定二圆管的轴分别共面的辅助圆柱，并利用二轴共面的吴文俊公式实现了给定圆管的分两段三次光滑拼接。白根柱 [7] [8] 给出了两个轴线异面的圆柱面存在三次拼接曲面的充要条件，并给出了存在光滑拼接的三次曲面时，两个圆柱面系数之间的关系和两个轴线异面的圆柱面在与轴线斜交的平行平面截口处若干种情形不存在光滑拼接曲面。Hartmann [9] 研究了基于轴线光滑拼接的方法对于轴线相交的管道进行光滑拼接。白根柱等 [10] - [16] 提出了基于轴线光滑拼接的轴线异面管道光滑拼接技术，主要集中在以Bézier曲线为轴线的管道、以推广的Hartmann曲线为轴线的管道、以锥面交线为轴线的管道光滑拼接两个轴线异面的管道和用各种螺旋线为轴线的管道光滑拼接两个轴线异面的管道方面的工作。

设 $C Y L_{1}$ 和 $C Y L_{2}$ 为以 $L_{1}$ 和 $L_{2}$ 为轴线的给定二管道的参数表示， $P_{1}, P_{2}$ 为给定的平面的参数表示，它们确定的曲面分别表示为 $s (C Y L_{i}) (i = 1, 2)$ ，其中 $s (P_{i}, C Y L_{i}) (i = 1, 2)$ 分别为柱面和平面的交线。

设 $s (P_{i}) (i = 1, 2)$ 为与 $s (C Y L_{i}) (i = 1, 2)$ 的轴线垂直的平面，则

$\begin{array}{l} P_{1} = A_{1} (x - X_{1}) + B_{1} (y - Y_{1}) + C_{1} (z - Z_{1}), \\ P_{2} = A_{2} (x - X_{2}) + B_{2} (y - Y_{2}) + C_{2} (z - Z_{2}) . \end{array}$

在上述基本假设下，我们研究存在圆柱螺旋管CH，并分别与 $s (P_{i}) (i = 1, 2)$ 在 $s (C Y L_{i}, P_{i})$ 处光滑拼接的条件，并给出拼接曲面的表达式。

2. 有理Bézier曲线及其性质

拟用以有理Bézier曲线为轴线的管道光滑拼接两个轴线异面的管道。在文献中构造了以Bézier曲线为轴线的光滑拼接两个轴线异面的管道的过渡曲面。Bézier曲线具备很多有点，但是不能调整曲线的局部形状，也不能精确表示一些二次曲线。有理Bézier曲线是Bézier曲线的推广，在保持控制顶点不变的前提下，有理Bézier曲线既可以整体修改曲线形状，又能精确表示

圆锥曲线。因此有理Bézier曲线在曲线、曲面拼接中有更广泛的应用。

定义给定 $n$ 个控制顶点 $V_{i} (i = 0, 1, \dots, n)$ ，对 $t \in [0, 1]$ 定义曲线

$r (t) = \sum_{i = 0}^{n} B_{n, i} (t) V_{i},$

和

$r (t) = \frac{\sum_{i = 0}^{n} B_{n, i} (t) w_{i} V_{i}}{\sum_{i = 0}^{n} B_{n, i} (t) w_{i}}$

分别为 $n$ 次Bézier曲线和 $n$ 次有理Bézier曲线。其中 $B_{n, i} (t), i = 0, 1, \dots, n$ 为Bernstein基函数， $w_{i} \neq 0, i = 0, 1, \dots, n$ 对应控制顶点的权因子。有理Bézier曲线和Bézier曲线一样通过首、末顶点并和特征多边形的首、末两条边相切。除此之外还具有以下特性：

1) 若权因子有正、有负，则出现数值不稳定现象；

2) 若权因子同号并取互为相反的两组数，所得有理Bézier曲线重叠，以下假设 $w_{i} > 0, i = 0, 1, \dots, n$ ；

3) 若所有权因子取相同的数 $w_{1} = w_{2} = \dots = w_{n} = k > 0$ ，则有理Bézier曲线退化为Bézier曲线；

4) 若 $0 < w_{i} < 1, i = 0, 1, \dots, n$ ，则所得有理Bézier曲线远离控制多边形；

5) 若 $w_{i} > 1, i = 0, 1, \dots, n$ ，则所得Bézier曲线靠近控制多边形，见图1，图2。

Figure 1. (Case of $w_{0} = 1, w_{1} = w_{2} = - 30, w_{3} = 1$ and $w_{0} = 1, w_{1} = - 2, w_{2} = 20, w_{3} = - 3$ )

图1. ( $w_{0} = 1, w_{1} = w_{2} = - 30, w_{3} = 1$ 和 $w_{0} = 1, w_{1} = - 2, w_{2} = 20, w_{3} = - 3$ 的情形)

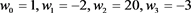
Figure 2. (Case of $w_{0} = w_{1} = w_{2} = w_{3} = \frac{1}{2}$ and $w_{0} = 2, w_{1} = 20, w_{2} = 20, w_{3} = 2$ )

图2. ( $w_{0} = w_{1} = w_{2} = w_{3} = \frac{1}{2}$ 和 $w_{0} = 2, w_{1} = 20, w_{2} = 20, w_{3} = 2$ 的情形)

3. 构造基于轴线光滑拼接的管道拼接曲面

设 $L_{1} : {\begin{cases} x = X_{1} + A_{1} s, \\ y = Y_{1} + B_{1} s, \\ z = Z_{1} + C_{1} s . \end{cases}$ 和 $L_{2} : {\begin{cases} x = X_{2} + A_{2} s, \\ y = Y_{2} + B_{2} s, \\ z = Z_{2} + C_{2} s . \end{cases}$ 为两个给定管道的轴线的参数方程，这里的直线 $l_{1}$ 是过点

$O_{1} (X_{1}, Y_{1}, Z_{1})$ 且方向矢量为 $d_{1} (A_{1}, B_{1}, C_{1})$ ， $l_{2}$ 是过点 $O_{2} (X_{2}, Y_{2}, Z_{2})$ 且方向矢量为 $d_{2} (A_{2}, B_{2}, C_{2})$ 。则空间两直线 $l_{1}$ 和 $l_{2}$ 是异面直线的充要条件为

$| \begin{matrix} X_{2} - X_{1} & Y_{2} - Y_{1} & Z_{2} - Z_{1} \\ A_{1} & B_{1} & C_{1} \\ A_{2} & B_{2} & C_{2} \end{matrix} | \neq 0.$

设 $C Y L_{1}$ 和 $C Y L_{2}$ 为给定的二管道的参数表示， $P_{1}, P_{2}$ 为给定的平面的参数表示，它们确定的曲面分别表示为 $s (C Y L_{i})$ ， $s (P_{i}) (i = 1, 2)$ ， $s (C Y L_{i}, P_{i}) (i = 1, 2)$ 为管道和平面的交线。

为叙述方便， $C Y L_{1}$ 的轴线 $L_{1}$ 位于OXY平面上且与Y轴平行，可设过点 $V_{0} (x_{0}, y_{0}, 0)$ ， $V_{1} (x_{0}, 0, 0)$ ， $C Y L_{2}$ 的轴线 $L_{2}$ 位于OYZ平面上，可设过点 $V_{2} (0, y_{2}, 0)$ ， $V_{3} (0, y_{2}, z_{2})$ ，于是参数表示分别为

$L_{1} : {\begin{cases} x = x_{1} + 0 s, \\ y = y_{1} + B_{1} s, \\ z = 0 + 0 s . \end{cases}$ 和 $L_{2} : {\begin{cases} x = 0 + 0 s, \\ y = y_{2} + 0 s, \\ z = z_{2} + C_{2} s . \end{cases}$

则管道方程分别为

${\begin{cases} x = X_{1} + a \cos t + a \sin t, \\ y = Y_{1} + B_{1} s + a \cos t + a \sin t, \\ z = a \cos t + a \sin t . \end{cases}$ 和

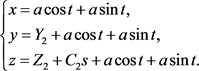
$t \in [0, 2 π]$ 其中 $a$ 为管道的半径。在这种假设下，先构造光滑拼接轴线的曲线，进而构造光滑拼接两个轴线异面的管道的拼接曲面。

根据有理Bézier曲线的性质，构造以 $V_{0}, V_{1}, V_{2}, V_{3}$ 为控制顶点的三次有理Bézier曲线

${\begin{cases} X = \frac{(- u^{3} + 3 u^{2} - 3 u + 1) w_{0} x_{0} + (3 u^{3} - 6 u^{2} + 3 u) w_{1} x_{1} + (- 3 u^{3} + 3 u^{2}) w_{2} x_{2} + u^{3} w_{3} x_{3}}{(- u^{3} + 3 u^{2} - 3 u + 1) w_{0} + (3 u^{3} - 6 u^{2} + 3 u) w_{1} + (- 3 u^{3} + 3 u^{2}) w_{2} + u^{3} w_{3}}, \\ Y = \frac{(- u^{3} + 3 u^{2} - 3 u + 1) w_{0} y_{0} + (3 u^{3} - 6 u^{2} + 3 u) w_{1} y_{1} + (- 3 u^{3} + 3 u^{2}) w_{2} y_{2} + u^{3} w_{3} y_{3}}{(- u^{3} + 3 u^{2} - 3 u + 1) w_{0} + (3 u^{3} - 6 u^{2} + 3 u) w_{1} + (- 3 u^{3} + 3 u^{2}) w_{2} + u^{3} w_{3}}, \\ Z = \frac{(- u^{3} + 3 u^{2} - 3 u + 1) w_{0} z_{0} + (3 u^{3} - 6 u^{2} + 3 u) w_{1} z_{1} + (- 3 u^{3} + 3 u^{2}) w_{2} z_{2} + u^{3} w_{3} z_{3}}{(- u^{3} + 3 u^{2} - 3 u + 1) w_{0} + (3 u^{3} - 6 u^{2} + 3 u) w_{1} + (- 3 u^{3} + 3 u^{2}) w_{2} + u^{3} w_{3}} . \end{cases}$

则此曲线光滑拼接轴线异面管道的轴线 $L_{1}$ 和 $L_{2}$ 。

这样，可以构造轴线异面的管道 $s (C Y L_{1})$ 和 $s (C Y L_{2})$ 在通过点 $V_{0}$ 和 $V_{3}$ 并与 $L_{1}$ 和 $L_{2}$ 垂直的平面处光滑拼接的管道。其拼接管道的参数表示为

$p (u, t) = {\begin{cases} X + a N_{1} (u) \cos t + a B_{1} (u) \sin t, \\ Y + a N_{2} (u) \cos t + a B_{2} (u) \sin t, \\ Z + a N_{3} (u) \cos t + a B_{3} (u) \sin t . \end{cases}$

其中 $a$ 为拼接管道的半径， $N (u) = (N_{1} (u), N_{2} (u), N_{3} (u))$ 和 $B (u) = (B_{1} (u), B_{2} (u), B_{3} (u))$ 分别为拼接管道在点 $u \in [0, 1]$ 处的法矢和副法矢。

4. 拼接实例

分异面角等于 $\frac{π}{2}$ ，小于 $\frac{π}{2}$ 和大于 $\frac{π}{2}$ 三种情形，给出拼接实例。可适当调整有理Bézier曲线的权因子，

使拼接管道的轴线远离控制多边形或靠近控制多边形，便于应用。

例1：设轴线异面管道的轴线分别为 $L_{1} : {\begin{cases} x = 3, \\ y = - 4 + t, \\ z = 0. \end{cases}$ 和 $L_{2} : {\begin{cases} x = 0, \\ y = 5, \\ z = 6 + t . \end{cases}$ 管道半径为1，有理Bézier曲线

的权因子取 $w_{0} = 1, w_{1} = 10, w_{2} = 10, w_{3} = 1$ 时，通过点 $V_{0} (3, - 4, 0)$ 和 $V_{3} (0, 5, 6)$ 并与 $L_{1}$ 和 $L_{2}$ 垂直的平面处光滑拼接的管道，图3。

例2：设轴线异面管道的轴线分别为 $L_{1} : {\begin{cases} x = 3, \\ y = - 4 + t, \\ z = 0. \end{cases}$ 和 $L_{2} : {\begin{cases} x = 0, \\ y = 3 - 2 t, \\ z = 6 + 6 t . \end{cases}$ 管道半径为1，有理Bézier曲线

的权因子取 $w_{0} = 1, w_{1} = 3, w_{2} = 3, w_{3} = 1$ 时，通过点 $V_{0} (3, - 4, 0)$ 和 $V_{3} (0, 3, 6)$ 并与 $L_{1}$ 和 $L_{2}$ 垂直的平面处光滑拼接的管道，图4。

例3：设轴线异面管道的轴线分别为 $L_{1} : {\begin{cases} x = 3, \\ y = - 4 + t, \\ z = 0. \end{cases}$ 和 $L_{2} : {\begin{cases} x = 0, \\ y = 8 + 3 t, \\ z = 6 + 6 t . \end{cases}$ 管道半径为1，有理Bézier曲线

的权因子取 $w_{0} = 1, w_{1} = 8, w_{2} = 8, w_{3} = 1$ 时，通过点 $V_{0} (3, - 4, 0)$ 和 $V_{3} (0, 8, 6)$ 并与 $L_{1}$ 和 $L_{2}$ 垂直的平面处光滑拼接的管道，图5。

尽管用有理Bézier曲线为轴线的管道能够光滑拼接轴线异面的圆管道，但是还不能够用隐式曲面轴线异面的管道。

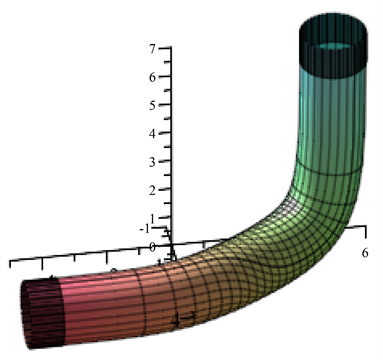
Figure 3. Blending of two tubes with non-coplanar axes when the dihedral angle pi/2

图3. 异面角为 $\frac{π}{2}$ 情形两个异面管道光滑拼接

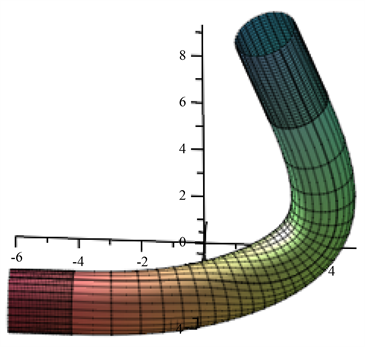
Figure 4. Blending of two tubes with non-coplanar axes when the dihedral angle is smaller than pi/2

图4. 异面角小于 $\frac{π}{2}$ 情形两个异面管道光滑拼接

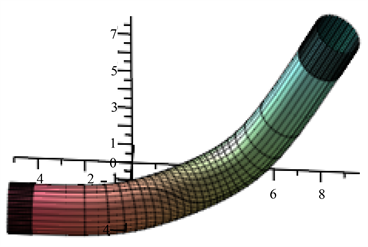
Figure 5. Blending of two tubes with non-coplanar axes when the dihedral angle is larger than pi/2

图5. 异面角大于 $\frac{π}{2}$ 情形两个异面管道光滑拼接

5. 结束语

本文利用有理Bézier曲线光滑拼接两个轴线异面的圆管道的轴线 $L_{1}$ 和 $L_{2}$ ，在此基础上实现了两个半径相同的轴线异面圆管道的 $G^{1}$ 光滑拼接。而对于半径不同轴线异面圆管道问题用此方法只能做到 $G^{0}$ 拼接。因此，有必要研究基于轴线光滑拼接的半径不同轴线异面管道的光滑拼接问题。

基金项目

浙江省教育厅一般项目资助(Y201636628)，国家自然科学基金项目资助(11561052)。

文章引用

王芳,白根柱. 有理Bézier曲线及其应用
Rational Bézier Curve and Its Application[J]. 应用数学进展, 2017, 06(08): 935-941. http://dx.doi.org/10.12677/AAM.2017.68112

参考文献 (References)

1. Warren, J. (1989) Blending Algebraic Surfaces. ACM Transactions on Graphics, 8, 263-278.
https://doi.org/10.1145/77269.77270

2. 吴文俊, 王定康. CAGD中的代数曲面拟合问题[J]. 数学的实践与认识, 1994(3): 26-31.

3. Wallner, J. and Pottmann, H. (1997) Rational Blending Surfaces between Quadrics. CAGD, 14, 407-419.

4. Wu, T.R. and Zhou. Y.S. (2000) On Blending of Several Quadratic Algebraic Surfaces. CAGD, 17, 759-766.

5. Cheng, J.S. (2003) Blending Quadric Surfaces via a Base Curve Method. In: Proceedings of ASCM03, World Scientific, Beijing, 17-19 April 2003, 77-86.
https://doi.org/10.1142/9789812704436_0007

6. 雷娜, 崔丽, 伍铁如. 两个轴异面的管道拼接[J]. 吉林大学学报(理学版), 2002, 40(2): 138-140.

7. 白根柱. 两个轴异面圆柱面的光滑拼接问题[D]: [硕士学位论文]. 长春: 吉林大学, 2004.

8. 白根柱. 隐式代数曲面拼接[J]. 数学的实践与认识, 2006, 36(4): 274-277.

9. Hartmann, E. (2001) Gn-Continuous Connections between Normal Ringed Surfaces. Computer Aided Geometric Design, 18, 751-770.

10. Bai, G.Z., Wang, H. and Yin, Z.J. (2014) Employing Generalized Bézier Tube to Smoothly Blending Tubes Whose Axes Are Non-Coplanar. Applied Mechanics and Mate-rials, 513-517, 2301-2306.

11. Wang, H. and Bai, G.Z. (2013) Employing Generalized Cylindrical Helicoid Tube to Smoothly Blending Tubes Whose Axes are Non-Coplanar. Applied Mechanics and Materials, 380-384, 1750-1754.

12. Bai, G.Z. and Wu, Z. (2013) Multi-Degree Reduction Approximation of Bézier Curves by Subdivision Method. Intelligent Information Management Systems and Technologies, 9, 37-42.

13. Bai, G.Z., Liu, S.Y., Wang, H., Wu, Z. and Yin, Z.J. (2014) A Novel Method for Smooth Blending Cylindrical Surfaces Whose Axes Are Non-Coplanar Based on Smooth Blending Axes. Applied Mechanics and Materials, 687-691, 1470-1473.

14. Bai, G.Z., Wang, H., Wu, Z., Yin, Z.J. and Liu, S.Y. (2015) Smoothly Blending of Two Elliptic Cylinders Whose Axes are Non-Coplanar. Applied Mechanics and Materials, 713-715, 152-158.

15. 刘斯语, 白根柱. 利用推广的Hartmann方法光滑拼接两个异面直线[J]. 内蒙古民族大学学报(自然科学版), 2015(2): 102-104.

16. 邱梦鸾, 肖琳, 白根柱. 用单页双曲螺旋管实现两个轴异面管道的光滑拼接[J]. 重庆师范大学学报(自然科学版), 2016(2): 108-112.

期刊菜单