Dynamical Systems and Control
Vol.05 No.03(2016), Article ID:18004,10
pages
10.12677/DSC.2016.53010
Computation of the Simplest Normal Form and Its Application
Shuping Chen
College of Applied Mathematics, Xiamen University of Technology, Xiamen Fujian

Received: Jun. 25th, 2016; accepted: Jul. 15th, 2016; published: Jul. 18th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper presents a new computation method for obtaining a significant refinement of the simplest normal form for four dimensional nonlinear systems. The formulae are derived, which can be used to compute the coefficients of the simplest normal form and the associated nonlinear transformation. By using the simplest normal form theory, the stability analysis of a simply-sup- ported functionally graded materials (FGMs) rectangular plate subject to the transversal and in- plane excitations is investigated. It is seen that the stability is exhibited under certain circumstances. The fourth-order Runge-Kutta algorithm is utilized to do numerical simulation of the stability behavior of the FGM rectangular plate.
Keywords:Functionally Graded Materials, Normal Form, Stability, Nonlinear Transformations

最简规范形的计算及其应用
陈淑萍
厦门理工学院应用数学学院,福建 厦门

收稿日期:2016年6月25日;录用日期:2016年7月15日;发布日期:2016年7月18日

摘 要
本文提出了计算四维非线性系统最简规范形的新方法,得到了计算四维非线性系统最简规范形的通用公式,并将该方法用于计算受横向和面内载荷共同作用的功能梯度材料矩形板系统的平均方程。理论结果表明,功能梯度材料矩形板系统在区域I内是稳定的,最后,利用四阶Rung-Kutta算法对功能梯度材料矩形板系统的稳定性行为进行数值模拟。
关键词 :功能梯度材料,规范形,稳定性,非线性变换

1. 引言
力学、航空航天和机械工程领域中,许多问题的力学模型可用高维非线性系统来描述。规范形理论是研究动力系统动力学特征的强有力工具,它的基本思想是在奇点附近经过一系列光滑的非线性变换把非线性系统在奇点附近简化为尽可能简单的形式,其实质是消去起次要作用的非线性项,同时,变换前后的非线性系统保持拓扑等价 [1] - [3] 。
规范形的概念,最早是由Poincare [4] 提出的。经过一个多世纪的发展,传统规范形理论已日趋成熟。关于规范形理论与计算在力学领域特别是非线性振动中的应用,国内外学者对此做了大量研究:文献 [5] [6] 利用规范形理论研究了非平面非线性运动悬臂梁的多脉冲和混沌动力学,粘弹性传动带的多脉冲轨道和混沌动力学;文献 [7] 利用规范形理论研究了单级倒立板系统的稳定性和混沌动力学;文献 [8] 将规范形理论应用于非线性振动减震器模型的全局分叉与动态混沌,研究了该系统的全局分叉和Shilnikov型混沌。
分叉理论是非线性科学的一个重要分支,近年来,国内外不少学者对非线性系统的分叉与稳定性进行了深入地研究,并取得了许多研究成果。文献 [9] 利用数值积分方法求解了系统分叉后的周期解,并对高速客车系统的横向稳定性问题进行了分析;文献 [10] 利用规范形理论和稳定性理论研究了种群生态系统的局部性态和全局稳定性文献 [11] 利用打靶法分析了非线性轮对陀螺系统的Hopf分叉,分析了陀螺力对蛇行运动稳定性的影响;文献 [12] 讨论了一类具有饱和发生率和饱和治愈率的SIR传染病模型的稳定性和分叉行为。
关于低维非线性动力系统最简规范形的计算已有很多研究,但对高维非线性系统最简规范形的研究相对较少。文献 [13] 研究了2维和3维非线性系统最简规范形的计算。本文在此基础上研究了四维非线性系统的最简规范形计算,并将理论结果应用于功能梯度材料矩形板系统,讨论了线性部分具有一对零特征值的功能梯度材料矩形板系统的稳定性问题。
2. 四维非线性系统的最简规范形计算
对于微分方程
 ,
, , (1)
, (1)
其中 为3阶非线性项。假定原点
为3阶非线性项。假定原点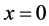 是一个奇点,即有
是一个奇点,即有 。
。
引进非线性变换
 , (2)
, (2)
将式(2)代入式(1),有
 ,(3)
,(3)
令
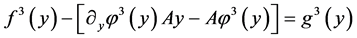 , (4)
, (4)
我们定义线性算子 如下:
如下:
 ,
,
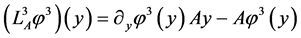 ,
, 。 (5)
。 (5)
令 是
是 的值域,
的值域, 是
是 在
在 中的任意补空间,则有
中的任意补空间,则有
 。 (6)
。 (6)
当 并不唯一时,我们可以利用它来进一步化简
并不唯一时,我们可以利用它来进一步化简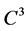 中的一些非线性项,因此,定义如下非线性算子
中的一些非线性项,因此,定义如下非线性算子
 且
且 。 (7)
。 (7)
令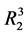 为算子
为算子 的一个值域,
的一个值域, 为
为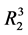 在
在 中的一个补空间,有
中的一个补空间,有
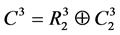 。 (8)
。 (8)
如果我们适当选择 ,使得
,使得 ,且
,且 ,则存在
,则存在 ,使(1)式转化为
,使(1)式转化为
 , (9)
, (9)
其中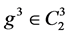 。
。
本文讨论线性部分具有一对零特征值,一对纯虚特征值情况,其中
 , (10)
, (10)
令
 ,
, ,
,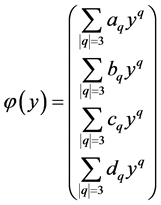 ,(11)
,(11)
将式(10)和(11)代入式(7),得到
 , (
, (
 , (12b)
, (12b)
 , (
, (
 。 (12d)
。 (12d)
令
 ,
,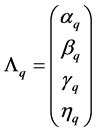 ,
, 。 (13)
。 (13)
由式(12)和式(13),得到
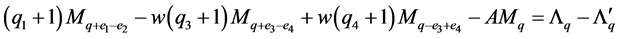 。 (14)
。 (14)
令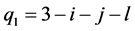 ,
,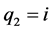 ,
, ,
,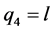 ,则有
,则有
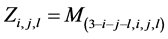 ,
, ,
,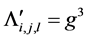 。 (15)
。 (15)
将式(15)代入式(14),得到
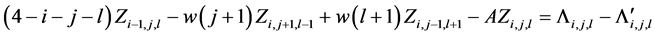 。 (16)
。 (16)
则由式(16)得到,
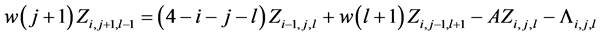 。 (17)
。 (17)
对应的余项为(当 )
)
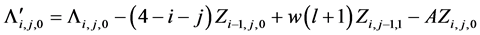 。 (18)
。 (18)
3. 功能梯度材料矩形板模型
对于如图1的功能梯度材料矩形板,直角坐标系位于功能梯度材料矩形板的中面,板沿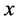 、
、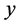 、
、 方向的几何尺寸分别为
方向的几何尺寸分别为 ,
, ,
, 。此功能梯度材料板受到横向和面内载荷共同作用,其中
。此功能梯度材料板受到横向和面内载荷共同作用,其中
 表示板沿着厚度方向的面内载荷,
表示板沿着厚度方向的面内载荷, 为横向载荷。
为横向载荷。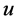 ,
,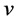 ,
, 表示板内
表示板内
任意一点在 ,
, ,
, 方向的位移,
方向的位移,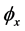 和
和 表示板中面法线相对
表示板中面法线相对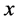 ,
, 轴的转角。功能梯度材料的非线性动力学方程为 [14] - [16]
轴的转角。功能梯度材料的非线性动力学方程为 [14] - [16]
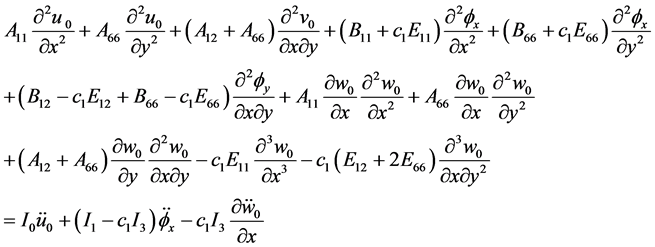 , (
, (
 , (19b)
, (19b)
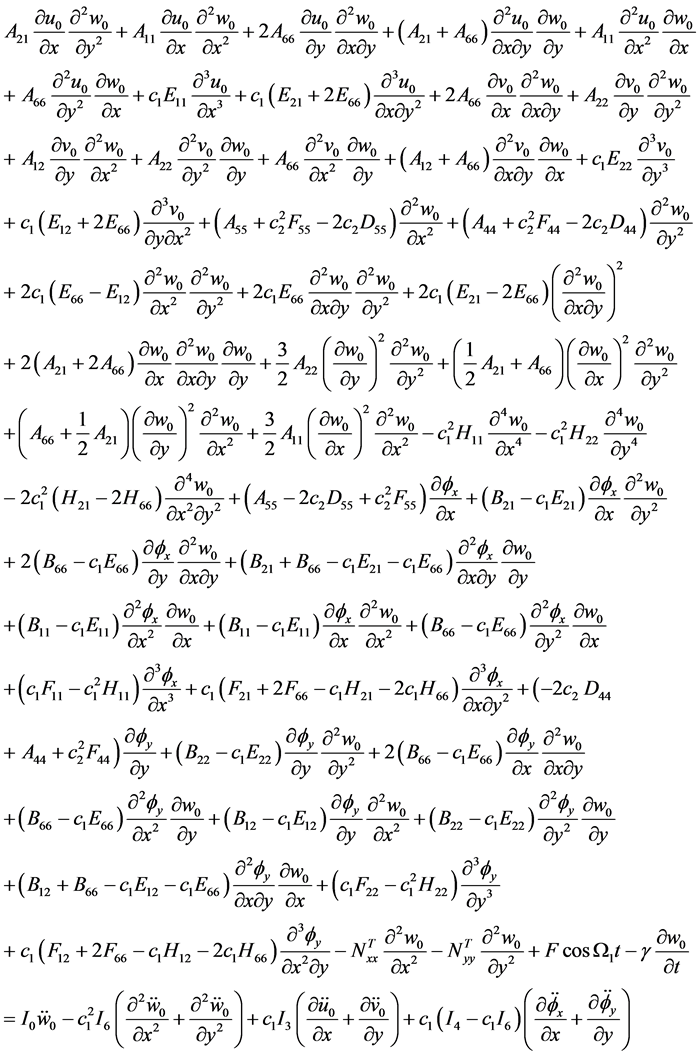 , (
, (
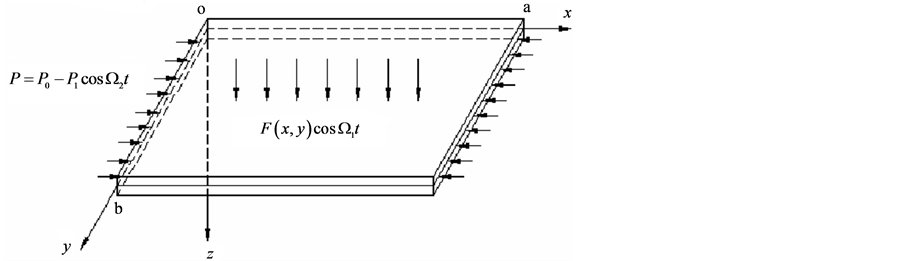
Figure 1. The model of a functionally graded materials rectangular plate
图1. 功能梯度材料矩形板模型
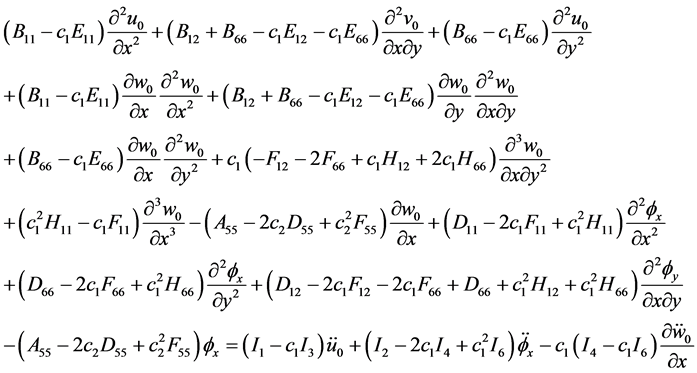 , (19d)
, (19d)
 。(19e)
。(19e)
其中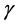 为阻尼系数。
为阻尼系数。
功能梯度材料板的边界条件表示为
 与
与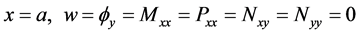 , (
, (
 与
与 , (20b)
, (20b)
 ,
, , (
, (
考虑主参数共振和1:2内共振,即,
 ,
,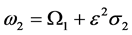 ,
,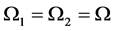 , (21)
, (21)
其中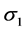 ,
, 为调谐参数。
为调谐参数。
使用Galerkin方法,并引入无量纲变量,得到无量纲化后的二自由度非线性动力学方程如下:
 , (
, (
 , (22b)
, (22b)
利用渐进摄动法,得到系统直角坐标下的平均方程为
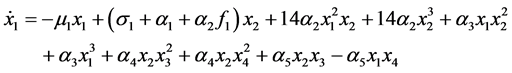 , (
, (
 , (23b)
, (23b)
 , (
, (
 。 (23d)
。 (23d)
4. 功能梯度材料矩形板的稳定性分析
在这一节,我们将利用改进的规范形方法,研究复合材料层合悬臂板的稳定性。系统(23)对应的特征多项式为
 , (24)
, (24)
其中
 (25)
(25)
其中 ,
,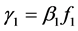 。
。
利用赫尔维茨判据 [17] ,有
 ,
, ,
, ,
, 。 (26)
。 (26)
显然,当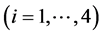
 时,系统的初始平衡点是稳定的。
时,系统的初始平衡点是稳定的。
本节主要讨论线性部分具有一对零特征根时系统的稳定性。
对于系统(23),取如下参数值:
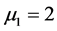 ,
, ,
, ,
, ,
,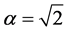 ,
, ,
,
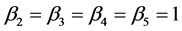 。 (27)
。 (27)
则系统(23)具有一对零特征值,引入新变量
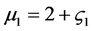 ,
, , (28)
, (28)
将式(28)代入式(24),得到
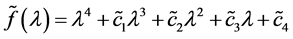 , (29)
, (29)
其中
 (30)
(30)
则对应的稳定性条件为
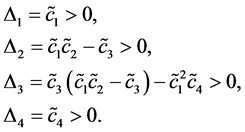 (31)
(31)
因此,我们可以得到如下四条缓和曲线
 (32)
(32)
如图2所示,在区域I内,初始平衡点是稳定的。
为了研究系统的非线性运动特性,利用改进的规范形方法对平均方程(23)进行化简,并利用龙格库塔方法进行数值模拟,见图3。系统在区域I内是稳定的,选取系统的参数值和初始条件如下:
 ,
,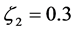 ,
, ,
, ,
, ,
, 。
。
其中,图(a)和(c)为相空间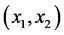 和
和 上的二维相图;图(b)为一阶模态振动特性的波形图;图(d)为二阶模态振动特性的波形图;图(e)为相空间
上的二维相图;图(b)为一阶模态振动特性的波形图;图(d)为二阶模态振动特性的波形图;图(e)为相空间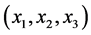 上的三维相图。
上的三维相图。
5. 小结
本文研究了四维非线性系统最简规范形的计算,对于线性部分具有一对零特征值的非线性系统,得到了计算其最简规范形的通用公式;利用改进的规范形方法,化简了受主参数共振和1:2内共振条件下的功能梯度材料矩形板系统的平均方程,研究了控制参数对系统稳定性的影响;最后,利用龙格库塔方法获得了系统的相图和波形图。此外,笔者仅利用改进的规范形方法研究了系统在奇点附近的稳定性,利用改进的规范形方法研究系统在奇点附近的分叉问题将作为今后的研究重点。
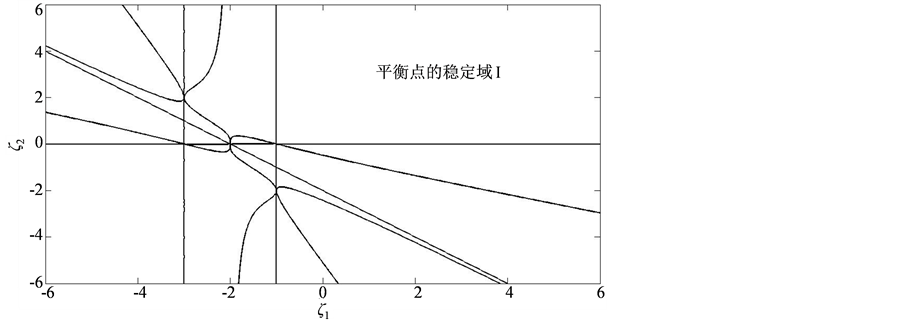
Figure 2. Transition curves of the system (23) for the case of a non-semisimple double zero eigenvalues
图2. 线性部分具有一对零特征根时系统的缓和曲线图

 (a) (b)
(a) (b)

 (c) (d)
(c) (d) (e)
(e)
Figure 3. Trajectory projection starting form initial point  when
when 
图3. 当参数 ,初始点
,初始点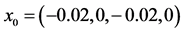 时,系统的运动轨迹
时,系统的运动轨迹
基金项目
国家自然科学基金青年基金项目11302184。
文章引用
陈淑萍. 最简规范形的计算及其应用
Computation of the Simplest Normal Form and Its Application[J]. 动力系统与控制, 2016, 05(03): 86-95. http://dx.doi.org/10.12677/DSC.2016.53010
参考文献 (References)
- 1. Bruno, A.D. (1989) Local Methods in Nonlinear Differential Equations. Springer-Verlag, Berlin, Heidelberg. http://dx.doi.org/10.1007/978-3-642-61314-2
- 2. Starzhinskii, V.M. (1980) Applied Methods in the Theory of Nonlinear Oscillations. Mir Publishers, Moscow.
- 3. Bruno, A.D. and Edneral, V.F. (2006) Normal Forms and Integrability of ODES Systems. Programming and Computer Software, 32, 139-144. http://dx.doi.org/10.1134/S0361768806030042
- 4. Poincaré, H. (1879) Sur les Propriétés des Fonctions Définies par des Equations aux Différences Partielles Thèse Inaugural. Gauthier-Villars.
- 5. Zhang, W. and Yao, M.H. (2006) Multi-Pulse Orbits and Chaotic Dynamics in Motion of Parametrically Excited Viscoelastic Moving Belt. Chaos, Solitons and Fractals, 28, 42-66. http://dx.doi.org/10.1016/j.chaos.2005.05.005
- 6. Zhang W., Wang, F.X. and Yao, M.H. (2005) Global Bifurcation and Chaotic Dynamics in Nonlinear Nonplanar Oscillations of a Parametrically Excited Cantilever Beam. Nonlinear Dynamics, 40, 251-279. http://dx.doi.org/10.1007/s11071-005-6435-3
- 7. Manuel, F.P., Manuel, P.M., Javier, G.C. and José, A.B. (2014) Stability and Chaotic Behavior of a PID Controlled Inverted Pendulum Subjected to a Harmonic Base Excitations by Using the Normal Form Theory. Applied Mathematics and Computation, 232, 698-718. http://dx.doi.org/10.1016/j.amc.2014.01.102
- 8. Zhang, W. and Li, J. (2001) Global Analysis for a Nonlinear Vibration Absorber with Fast and Slow Modes. International Journal of Bifurcation and Chaos, 11, 2179-2194. http://dx.doi.org/10.1142/S0218127401003334
- 9. 曾京, 徐涛. 客车系统非线性横向稳定性的分叉研究[J]. 西南交通大学学报, 1994, 29(3): 316-322.
- 10. 周稻详. 种群生态模型的分叉与稳定性研究[D]: [硕士学位论文]. 重庆: 重庆大学, 2013.
- 11. 张波, 曾京, 董浩. 非线性轮对陀螺系统的稳定性及分叉研究. 振动: 测试与诊断, 2015, 35(5): 955-960.
- 12. Erika, R., Eric, A. and Gerardo, G. (2016) Stability and Bifurcation Analysis of a SIR Model with Saturated Incidence Rate and Saturated Treatment. Mathematics and Computers Simulation, 121, 109-132. http://dx.doi.org/10.1016/j.matcom.2015.09.005
- 13. Chen, G. and Della Dora, J. (2000) Further Reductions of Normal Forms for Dynamical Systems. Journal of Differential Equations, 166, 79-106. http://dx.doi.org/10.1006/jdeq.2000.3783
- 14. Hao, Y.X., Zhang, W. and Yang, J. (2011) Analysis on Nonlinear Oscillations of a Cantilever FGM Rectangular Plate Based on Third-Order Plate Theory and Asymptotic Perturbation Method. Composites Part B: Engineering, 42, 402- 413. http://dx.doi.org/10.1016/j.compositesb.2010.12.010
- 15. Zhang, W., Song, C.Z. and Ye, M. (2006) Further Studies on Nonlinear Oscillations and Chaos of a Rectangular Symmetric Cross-By Laminated Plate under Parametric Excitation. International Journal of Bifurcation and Chaos, 16, 325-347. http://dx.doi.org/10.1142/S0218127406014836
- 16. Zhang, W., Hao, Y.X., Guo, X.Y. and Chen, L.H. (2012) Complicated Nonlinear Response of a Simply Supported FGM Rectangular Plate under Combined Parametric and External Excitations. Mecanica, 47, 985-1014. http://dx.doi.org/10.1007/s11012-011-9491-4
- 17. Ogata, K. (1970) Modern Control Engineering. Prentice-Hall, Englewood Cliffs.