Nuclear Science and Technology
Vol.04 No.02(2016), Article ID:17451,9
pages
10.12677/NST.2016.42006
Study on the Transient Neutron Diffusion Equation Solving Method Based on Exponential Transform
Bo Pang, Qiang Zhao, Chen Hao, Yan Yu
Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin Heilongjiang

Received: Apr. 8th, 2016; accepted: Apr. 22nd, 2016; published: Apr. 27th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Transient diffusion equation solution method based on exponential transform is studied mainly. Time integral aspect exponential transform weakens the influence of the stiff problem, and the time integration method is used to improve calculation accuracy. Fine mesh finite difference method is taken to improve the geometry calculation accuracy, and conjugate gradient squared method is used for solving final equations. Based on the above methods, multi-group neutron kinetics model calculation program is developed.
Keywords:Neuron Kinetics Model, Exponential Transform, Time Integration Method, Conjugate Gradient Squared Method

基于指数变换的瞬态扩散方程求解方法研究
庞博,赵强,郝琛,宇炎
哈尔滨工程大学核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨

收稿日期:2016年4月8日;录用日期:2016年4月22日;发布日期:2016年4月27日

摘 要
本文重点研究了基于指数变换的瞬态扩散方程求解方法,时间上采用指数变换减弱刚性问题的影响,并采用时间积分法提高计算精度。几何上采取细网有限差分以提高计算精度,并且采用平方共轭梯度法进行最后的方程组求解。本文基于上述方法开发了三维多群中子时空动力学计算程序。
关键词 :中子时空动力学,指数变换,时间积分法,共轭平方法

1. 引言
中子时空动力学模型是一个刚性模型。求解中子时空动力学模型时,常常将其简化为点堆模型。基于点堆模型提出了如下求解方法:吉尔算法、刚性限制方法(SCM)、线性多步法、四阶隐式龙格库塔法等。在多维的时空动力学求解时,有两种思路:一种是对多维时空动力学方程进行时空分离,如改进准静态法是一个快速高效的求解方法 [1] ;另外一种是直接求解多维时空动力学方程,并采用处理刚性问题的方法,例如,采用θ法求解中子时空动力学方程 [2] ,这种方法用前一时刻的结果估计新的θ值;使用对角线格式的隐式四阶龙格库塔法求解中子瞬态扩散方程 [3] 。
本文采取直接求解三维时空动力学方程的思路。首先采用指数变换的方法减缓中子通量的变化速率,从而限制刚性问题。然后对指数变换后的方程采用时间积分法求解,最后采用平方共轭梯度法(CGS)求解细网差分离散后的方程组。
2. 中子时空动力学求解
2.1. 指数变换
在本文中为表述方便将中子时空动力学方程的扩散模型写成如下算子形式:
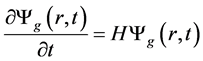 (1)
(1)
直接求解时空动力学问题会遇到刚性问题,直接求解时间步长不能选择过大,对于一般压水堆,显式求解方程(1)要选择10−4 s [4] ,使用θ法(θ = 0.5)计算能相对放大时间步长到10−3 s [2] 。为了进一步放大时间步长,采用指数变换减少中子通量的变化速度,采用指数变换后可以将时间步长进一步放大到10−2 s。具体方法如下:
将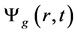 分解为如下乘积形式,
分解为如下乘积形式,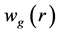 为指数变换系数。
为指数变换系数。
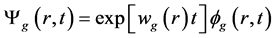 (2)
(2)
指数变换后的中子通量密度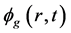 变化缓慢,能够解决由于中子通量变化速率快而导致的中子时空动力学方程的刚性问题,使得方程(1)更易求解。离散后的
变化缓慢,能够解决由于中子通量变化速率快而导致的中子时空动力学方程的刚性问题,使得方程(1)更易求解。离散后的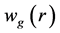 由式(3)求解 [5] 。
由式(3)求解 [5] 。
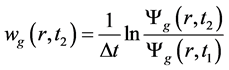 (3)
(3)
计算时我们希望,在沿着时间步长计算时所使用的公式为递推公式,所以在式(2)改写为如下形式。
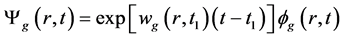 (4)
(4)
式中: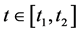 ;
;
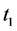 为当前步长起始时刻;
为当前步长起始时刻;
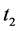 为当前步长结束时刻;
为当前步长结束时刻;
 为指数变换参数。
为指数变换参数。
为保证计算过程是单向的,避免求解一个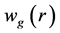 和
和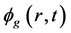 的耦合问题,选取
的耦合问题,选取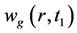 代替式(2)中的
代替式(2)中的 。将式(2)带入(1)中,得到指数变换后的通量计算表达式:
。将式(2)带入(1)中,得到指数变换后的通量计算表达式:
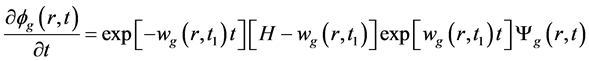 (5)
(5)
2.2. 时间积分方法
从上一节可知,在求解得到的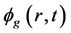 需要乘以一次指数形式才能得到真实的中子通量,为了减少这次指数变化导致的误差放大的问题,需要更精确的求解
需要乘以一次指数形式才能得到真实的中子通量,为了减少这次指数变化导致的误差放大的问题,需要更精确的求解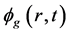 。为此本文采用时间积分法求解方程(5)。时间离散时,通常将时空动力学问题转化为求解带有固定源的稳态问题。
。为此本文采用时间积分法求解方程(5)。时间离散时,通常将时空动力学问题转化为求解带有固定源的稳态问题。 时刻通量和缓发中子先驱核分布为已知量,求解后的方程中
时刻通量和缓发中子先驱核分布为已知量,求解后的方程中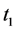 时刻相关量为固定源,其余各项的系数整理成求解方程组的系数矩阵。
时刻相关量为固定源,其余各项的系数整理成求解方程组的系数矩阵。
首先积分缓发中子,本文对缓发中子采取直接积分求解。在缓发中子积分过程中需要引入如下假设:在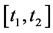 区间内,
区间内,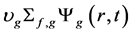 的变化关于t是线性的 [6] 。但是由于2.1中假设
的变化关于t是线性的 [6] 。但是由于2.1中假设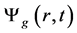 是指数变化形式,若假设
是指数变化形式,若假设 为线性变化与前面指数变换冲突,所以假设
为线性变化与前面指数变换冲突,所以假设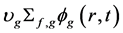 的变化关于t是线性的。同时也认为
的变化关于t是线性的。同时也认为 与各截面的乘积都关于时间t是线性变化;同时积分时采用梯形积分公式。缓发中子积分结果如下:
与各截面的乘积都关于时间t是线性变化;同时积分时采用梯形积分公式。缓发中子积分结果如下:
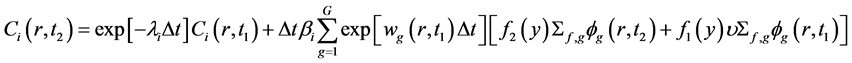 (6)
(6)
式中:
 ;
;
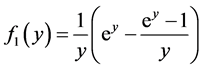 ;
;
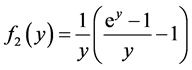 ;
;
指数变换后的通量的积分结果如下:
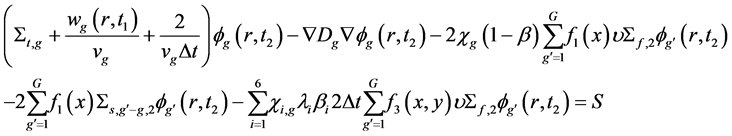 (7)
(7)
式中:S为固定源。
S由式(8)求解。
 (8)
(8)
式中: ;
;
 ;
;
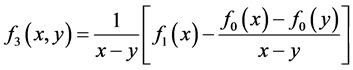 ;
;
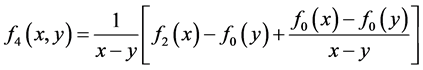 ;
;
由于x和y由待定参数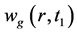 计算得到,不能保证在
计算得到,不能保证在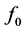 、
、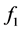 、
、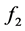 、
、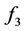 、
、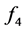 在计算过程中不出现分母为0的情况;而且如果分母的计算结果很小会导致函数计算结果失真。所以对
在计算过程中不出现分母为0的情况;而且如果分母的计算结果很小会导致函数计算结果失真。所以对 进行泰勒展开,计算化简后得到
进行泰勒展开,计算化简后得到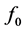 、
、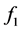 、
、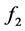 、
、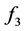 、
、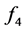 结果如下。
结果如下。
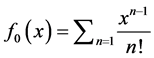 ;
;
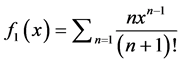 ;
;
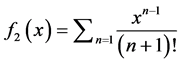 ;
;
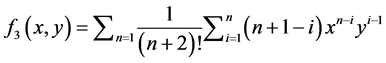 ;
;
 。
。
用泰勒展开得到的表达式计算方程(6)和(7)的计算参数,就避免了由于 而导致x或y等于0或趋近于0时,无法计算参数或者计算参数结果不稳定的情况。
而导致x或y等于0或趋近于0时,无法计算参数或者计算参数结果不稳定的情况。
2.3. 共轭平方法求解与矩阵压缩
由于放大了时间步长,再使用传统高斯赛德尔迭代时,收敛速度大幅减缓。本文为了加速收敛采用Krylov子空间法计算。
对所求的通量方程在空间上采取中心差分的形式离散。对于三维矩形网格,泄漏项展开成为7对角矩阵。由于通量方程能量上分为多群求解,不同能群之间存在散射和裂变关系。以二群为例,一群向二群散射的通量和二群裂变按能谱分配到一群的通量不同,导致最后得到的方程组系数矩阵是非对称的。
平方共轭梯度法是基于Lanczos双正交化的Krylov子空间法的一种。可以解决系数矩阵不对称时的线性方程组求解,并且求解过程具有和共轭梯度法一样的短迭代格式。短迭代格式能够减少计算过程中的存储量和每次迭代的计算量。平方共轭梯度法克服了Lanczos双正交化过程中需要计算系数矩阵转置的缺点。在系数矩阵需要压缩存储时计算更易实现。
设通过空间上积分离散后的系数矩阵为A,所求方程则为:
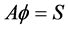 (9)
(9)
为求解方程(9),CGS迭代过程如下:
第一步,计算残量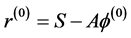 ,取
,取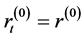 ,并且令
,并且令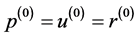 ,
,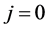 。
。
第二步,计算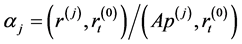 ,
, 。
。
第三步,计算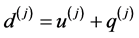 ,
,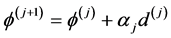 ,
, ,如果
,如果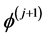 满足收敛条件,则跳出循环。
满足收敛条件,则跳出循环。
第四步,计算 ,并更新向量
,并更新向量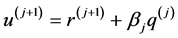 ,
,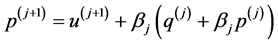 。令
。令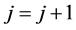 ,转第二步进行循环。
,转第二步进行循环。
可以看到CGS在求解过程中对A矩阵处理只需要进行矩阵乘向量计算,便于压缩矩阵的计算程序编写。在压缩存储时,本文采用两个矩阵A1,A2分别存储系数矩阵中不为0的参数。A1矩阵的每一行存储该行中不为0的参数的位置信息,A2存储相应的参数值。这样在矩阵与向量做内积运算中只需要在A1中找到系数矩阵中的参数位置信息,再在向量中找到相应位置的参数。这些参数与A2中的对应参数做内积运算即可完成矩阵乘向量的计算。这种压缩方式只存储不为0的参数,对于系数矩阵可以大大减少存储量和计算量。
3. 程序实现
根据第二章的介绍,程序主要流程如下。
第一步,先从输入卡中读入计算用参数。参数包括控制信息、几何信息、宏观计算界面、计算总时间、时间步长、缓发中子份额等;
第二步,在计算瞬态前首先计算初始状态的稳态通量分布,采用稳态计算结果作为初值有利于初始计算时瞬态计算的收敛;
第三步,然后计算指数变换后的通量分布,认为缓发中子在初始状态下偏导数为0,计算缓发中子先驱核的分布,计算总循环步数n,置循环变量t为1;
第四步,按式(8)计算固定源S;
第五步,按照截面参数随时间变化的情况,重新计算相应时间的系数矩阵A;
第六步,利用CGS求解器求解下一时刻的指数变化后的通量,其中收敛误差为10−6;
第七步,利用指数变化求解真实通量;
第八步,利用用式(6)求解缓发中子先驱核的密度,用式(3)更新指数变换系数;
第九步,计算并输出堆芯功率;
第十步,如果t = n那么跳出循环,程序终止;如果t < n那么循环变量t = t + 1,并返回第四步继续循环计算。
程序流程图如图1所示。
4. 数值验证
本文采用LMW算例进行三维堆芯验证。三维LMW问题模拟1/4对称堆芯的提棒和插棒过程,是一缓慢变化的瞬态过程。堆芯径向为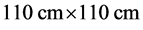 ,轴向高200 cm,其中,燃料区高160 cm,上、下各有20 cm的反射层。堆芯有两组控制棒,第1组控制棒0 s开始从堆芯内高100 cm处以3 cm/s的速度向上抽出,第2组棒在7.5 s时由堆芯活性区顶端以3 cm/s的速度插入,直到47.5 s停止;大约在20 s时堆芯功率达到峰值。计算分析堆芯从0 s到60 s的功率变化情况 [3] 。堆芯横截面示意图如图2所示,移动控制棒前后堆芯控制棒位置由图3所示。本文采用径向
,轴向高200 cm,其中,燃料区高160 cm,上、下各有20 cm的反射层。堆芯有两组控制棒,第1组控制棒0 s开始从堆芯内高100 cm处以3 cm/s的速度向上抽出,第2组棒在7.5 s时由堆芯活性区顶端以3 cm/s的速度插入,直到47.5 s停止;大约在20 s时堆芯功率达到峰值。计算分析堆芯从0 s到60 s的功率变化情况 [3] 。堆芯横截面示意图如图2所示,移动控制棒前后堆芯控制棒位置由图3所示。本文采用径向 网格划分轴向以2 cm网格划分。
网格划分轴向以2 cm网格划分。
瞬态过程在20秒左右达到峰值,比较峰值计算结果。直接采用θ法(θ = 0.5)和采用指数变换和缓发中子积分在20 s计算值时的结果如表1所示。
通过表1,可以看出指数变换和缓发中子积分的计算结果更为准确。而且在时间步长方面指数变换采用0.01 s为时间步长,而θ法(θ = 0.5)采用的是0.001 s作为时间步长。由此可以看出θ法中加入指数
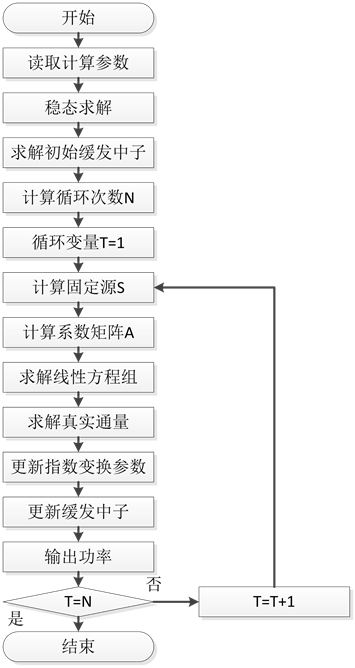
Figure 1. Program flow chart
图1. 程序流程图
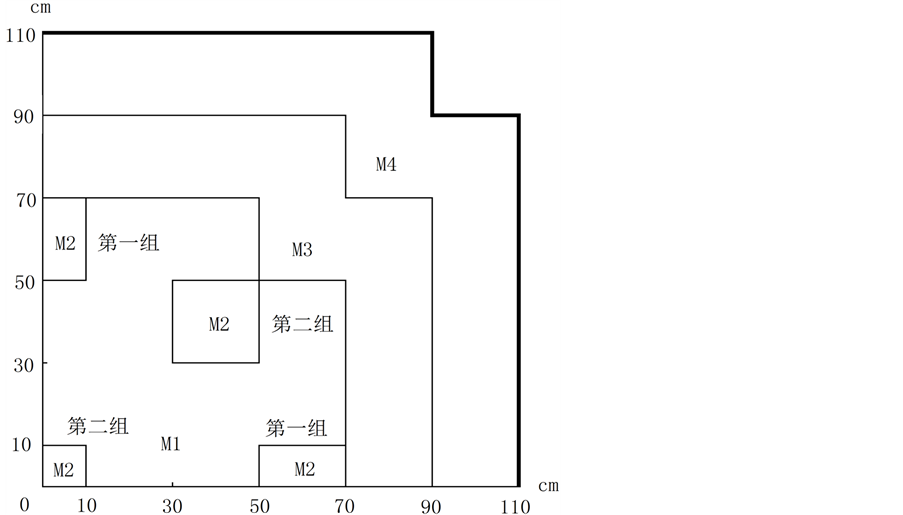
Figure 2. Radial sectional view of the reactor core
图2. 堆芯径向截面图
变换可以进一步放大时间步长,采用缓发中子积分能够减小误差。
放大时间步长后,对于传统迭代方法由于迭代矩阵的最大特征值更接近1,这导致传统的迭代方法如LSOR等,单次循环迭代次数大大增加,采用CGS计算方法能相对的减小迭代次数,如表2所示。
由表2可以看出CGS求解器迭代次数明显小于传统的LSOR算法求解器,能够起到加速计算的效果。
整体计算结果归一化功率变化如图4所示,横坐标轴为时间单位秒。整体计算结果关键点如表3所示,最大误差不超过2%,符合良好。
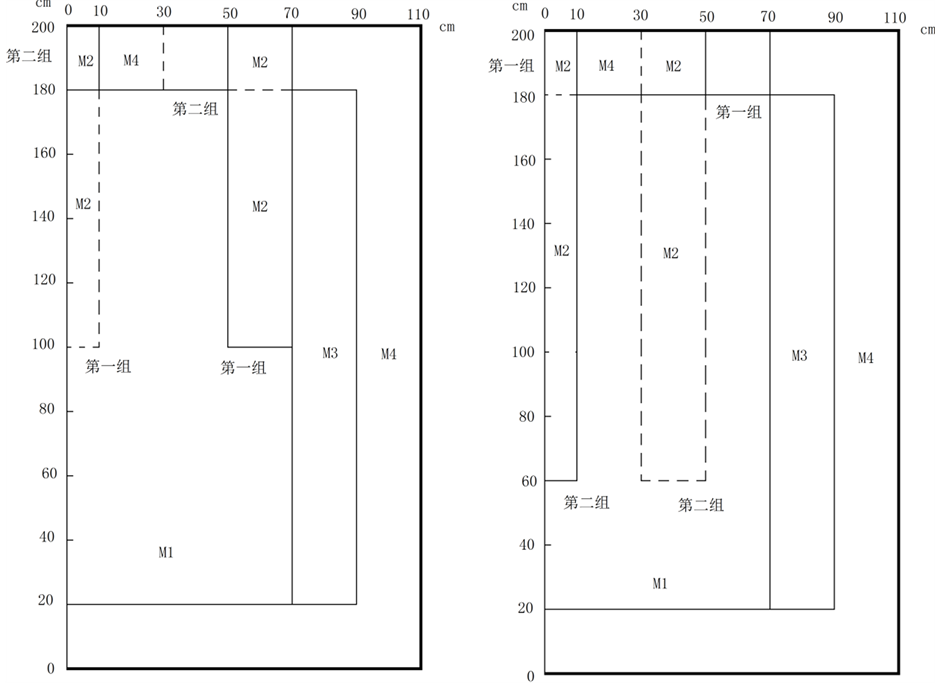
Figure 3. The initial rod position (left), final rod position (right)
图3. 初始控制棒棒位(左),最终控制棒棒位(右)
Table 1. LMW relative power comparison at 20 s
表1. LMW算例20 s相对功率比较
Table 2. The number of iterations, when the control rods in the first mesh movement
表2. 控制棒在第一个网格内运动时迭代次数比较
Table 3. LMW benchmark problem’s normalized power results
表3. LMW基准题归一化功率结果比较
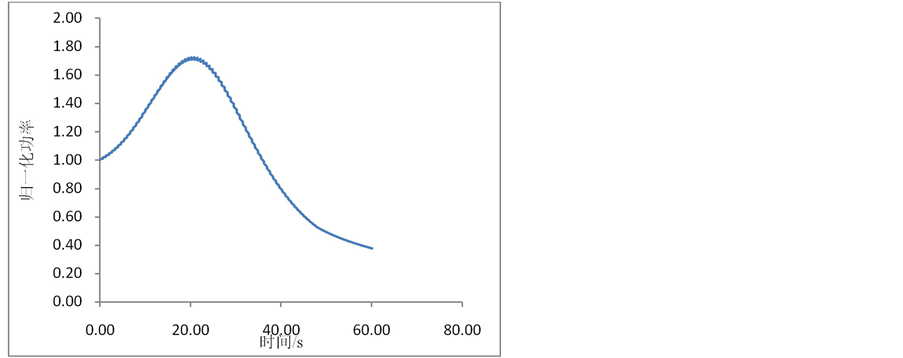
Figure 4. Normalized power value versus time results
图4. 归一化功率随时间变化结果
5. 结论
本文采用的先进行指数变换方法减缓中子通量的变化速率,然后采用时间积分法求解变换后的中子动力学方程的计算方法。经过与文献 [7] 中的计算结果比较,本文研究的求解中子动力学方程的方法及所开发的程序是正确的;与θ法(θ = 0.5)相比增大了时间步长,提高了计算精度;采取共轭平方法(CGS)与传统LSOR相比,减少了迭代次数。
指数变换方法能够减少中子通量离散过程中的截断误差,时间积分法避免了缓发中子先驱核的离散过程引入的截断误差。总体计算引入的系统误差小,能够适应反应堆物理提出的新的“高保真”要求。
准确性方面可以进一步提高空间离散的计算精度,采用输运的求解方法如MOC等,在细网条件下耦合求解更精确的功率分布。时间方面,指数变化后的方程可以采用比时间积分法这类二阶精度更高阶的积分方法来进一步提高计算精度。
在计算效率方面,可以采用先进的加速方法,如多重网格等,在精度不变的前提下提高计算速度。本文采用的求解器能够方便得在大型并行计算机上实现并行求解,这样也可以进一步提高计算速度。
文章引用
庞博,赵强,郝琛,宇炎. 基于指数变换的瞬态扩散方程求解方法研究
Study on the Transient Neutron Diffusion Equation Solving Method Based on Exponential Transform[J]. 核科学与技术, 2016, 04(02): 41-49. http://dx.doi.org/10.12677/NST.2016.42006
参考文献 (References)
- 1. 胡大璞. 求解中子时空动力学方程的动态反应性法[J]. 核动力工程, 1994, 15(1): 45-53.
- 2. 焦惠先, 李惠云. 小型压水堆弹棒事故反应性分析[J]. 核科学与工程, 1987, 7(3-4): 219.
- 3. 赵文博. 瞬态节块格林函数方法及其与热工–水力耦合研究[D]: [博士学位论文]. 北京: 清华大学, 2012.
- 4. 黄祖恰. 核反应堆动力学基础[M]. 北京: 北京大学出版社, 2007: 420-421.
- 5. Reed, W.H. and Hansen, K.F. (1970) Alternating Direction Methods for the Reactor Kinetics Equations. Nuclear Science and Engineering, 41, 431-442.
- 6. 谢仲生. 核反应堆物理数值计算[M]. 北京: 原子能出版社, 1997: 160.
- 7. Zimin, V.G. and Ninokata, H. (1998) Nodal Neutron Kinetics Model Based on Nonlinear Iteration Procedure for LWR Analysis. Annals of Nuclear Energy, 25, 507-528. http://dx.doi.org/10.1016/S0306-4549(97)00078-9
