Pure Mathematics
Vol.
14
No.
01
(
2024
), Article ID:
80320
,
6
pages
10.12677/PM.2024.141034
型为tr的5-半循环可分组设计
杜 珺1,黄月梅1,2*
1内蒙古师范大学数学科学学院,内蒙古 呼和浩特
2内蒙古自治区应用数学中心,内蒙古 呼和浩特
收稿日期:2023年11月27日;录用日期:2023年12月14日;发布日期:2024年1月31日

摘要
半循环可分组设计在组合编码中有着广泛的应用。根据半循环可分组设计的定义,给出型为tr,区组长度为5的半循环可分组设计存在的必要条件。再利用循环差阵、t-正则的循环填充及两种递归构造法,得到了型为tr,区组长度为5的半循环可分组设计存在的若干充分条件。
关键词
半循环可分组设计,循环差阵,循环填充,递归构造

Semi-Cyclic Group Divisible Design of Type tr with Block Size 5
Jun Du1, Yuemei Huang1,2*
1College of Mathematics Science, Inner Mongolia Normal University, Hohhot Inner Mongolia
2Inner Mongolia Center for Applied Mathematics, Hohhot Inner Mongolia
Received: Nov. 27th, 2023; accepted: Dec. 14th, 2023; published: Jan. 31st, 2024

ABSTRACT
Semi-cyclic group divisible design has many applications in combinatorial coding. The necessary condition of semi-cyclic group divisible design of type tr with block size 5 was obtained from the definition. In addition, several spectrums of semi-cyclic group divisible design with block size 5 were obtained by employing cyclic difference matrix, t-regular cyclic packing with the aid of two recursive constructions.
Keywords:Semi-Cyclic Group Divisible Design, Cyclic Difference Matrix, Cyclic Packing, Recursive Construction

Copyright © 2024 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
设 和k都是正整数, 且 表示模t剩余类加群。令 是点集 的k元子集族(基区组集)。对 中任意两个整数x和y及 中的k-子集B定义
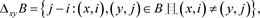
则 ,其中减法模t计算。 中的差称为 的 差。若当 时, ,
否则
,则称
是
上,组集为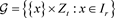 的一个型为tr的半循环可分组设计(semi-cyclic group divisible design),简记为k-SCGDD。
的一个型为tr的半循环可分组设计(semi-cyclic group divisible design),简记为k-SCGDD。
例1 令 , ,则下列7个区组构成型为75的5-SCGDD的基区组:
, ,
, ,
, ,
,
通过对以上七个基区组的每个元素的第二分量加1并模7运算就可以得到型为75的5-SCGDD的所有区组。
半循环可分组设计的定义由Yin J. [1] 提出。半循环可分组设计在其它设计和光正交码的构造中有重要的应用,因此它的存在性和组合构造问题被进行了系统地研究。Gallant R. P.等 [2] 解决了3-SCGDD存在的充要条件。Wang J. [3] 和Wang K. [4] 等给出型为 的k-SCGDD的递归构造方法,并解决了4-SCGDD
的存在问题。近期,Wang L.等 [5] 给出当p为奇素数,t为正整数时,型为 的 -SCGDD的存在条件。
目前关于5-SCGDD还没有独立的研究结果,因此本文对5-SCGDD的存在谱和构造问题进行了研究。首先从半循环可分组设计的定义出发,给出了型为tr的5-SCGDD存在的必要条件,再借助循环差阵和t-正则循环填充设计及递归构造方法得到了型为tr的5-SCGDD存在的部分充分条件,所得结果丰富了半循环可分组设计的研究内容。
2. 辅助设计及构造方法
半循环可分组设计的结构与循环差阵、循环填充及平衡不完全区组设计等设计有密切联系,下面给出相关设计的定义。
设 是正整数。一个循环差阵(CDM)是一个 阶矩阵 , ,且任意两行都满足 ,其中 , , ,记作 -CDM。
令 , , 是X的s个k元子集(基区组)的集合。若 包含 中的每个非零元至多一次,则 称为一个循环填充设计,记作CP 。特别地,若 可构成 的一个阶为t的加法子群,则CP 又记作t-正则CP 。在文献 [6] 中,t-正则CP 也被称作差族,简记为 -DF。
设 是正整数。一个平衡不完全区组设计,记作BIBD (或B ),是一个二元组 ,需满足条件:1) ;2) 对任意的 ,都有 ;3) X中任意两个不同的元素都恰好包含在λ个区组B中。
半循环可分组设计与以上几个设计之间的关系有如下几个结论。
引理1 [3] 型为tk的k-SCGDD与 -CDM等价。
引理2 [3] 若t-正则CP 存在,则存在型为tr的k-SCGDD。
以下是与半循环可分组设计有关的两个递归构造法。
构造法1 [3] 若型为tr和型为mk的k-SCGDD都存在,则存在型为 的k-SCGDD。
构造法2 [3] 若B 和型为tk的k-SCGDD存在,则存在型为tv的k-SCGDD。
以上两种构造方法具有一定的普适性,有助于我们得到更多类型的半循环可分组设计。
文献 [7] - [13] 中给出关于B 、 -CDM和t-正则CP 的存在条件如下:
引理3 [7] 当 且 时,B 存在。
引理4 [8] 当t是奇数, 且 时, -CDM存在;当 , 时, -CDM也存在。
引理5 [9] 当 ,t为偶数时, -CDM不存在; -CDM也不存在。
推论1 -CDM不存在。
证明:设A是一个 -CDM。由循环差阵的定义,移除A 任意一行得到一个 -CDM;因此,若 -CDM不存在,则 -CDM也不存在。由引理5可知, -CDM不存在,故 -CDM也不存在。
引理6 [10] [11] [12] [13] 设 是正整数,则对下列参数,t-正则CP 存在:
1) 当 或45, 是素数且 ;
2)当 ;
3) 当 或20, 是素数且 ;
4) 当 或12, 是素数;
5) 当 ,r是素数且 。
下面给出利用循环差阵、t-正则循环填充以及递归构造法构造半循环可分组设计的具体例子。
例2 型为55的5-SCGDD存在。
证:一个(5,5)-CDM如矩阵A所示:
.
可以验证,当
,
,
时,任意两行都满足
,符合循环差阵的定义。令
,
,其中
,则
构成点集
上,组集为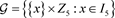 的型为55的5-SCGDD的基区组集。
的型为55的5-SCGDD的基区组集。
例3 若存在10-正则CP ,则存在型为109的5-SCGDD。
证明:文献 [10] 给出一个10-正则CP 的基区组集 ,其中四个区组为 , , , 。
对于任意的 ,令 , , ,则得到对应的二元组 。定义 为A的平移,
。对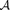 的四个区组及它们的平移做上述转换,则
构成点集
的四个区组及它们的平移做上述转换,则
构成点集
上,组集为 的型为109的5-SCGDD的基区组集。
例4 若型为75和型为55的5-SCGDD都存在,则型为355的5-SCGDD也存在。
证明:设型为75的5-SCGDD的点集
,组集
,基区组集
。对任意
,由例2,存在点集
上,组集为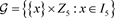 ,基区组集
的型为55的5-SCGDD。利用构造1,对任意的
,
,做
,基区组集
的型为55的5-SCGDD。利用构造1,对任意的
,
,做
.
再令
表示这些
构成的集合,其中
取遍
中的5个基区组,则
构成点集
上,组集 的型为355的5-SCGDD的基区组集。
的型为355的5-SCGDD的基区组集。
3. 型为tr的5-SCGDD的存在条件
这一小节将讨论型为tr的5-SCGDD的存在条件。
定理1 型为tr的5-SCGDD存在的必要条件是 , 且 。
证明:设 是一个型为tr的5-SCGDD。由可分组设计的定义,区组中的每个点取自不同的组,故 ;而包含点集中任意一个点x的区组个数为 ,又 为正整数,所以 。因为共有rt个点,所有的区组个数为 ,而每个区组轨道的长为t,所以基区组的个数为 ,因此 。
定理2 若t是奇数且 或9p,其中p是素数, 且 时,型为t5的5-SCGDD存在。当 或为偶数时,型为t5的5-SCGDD不存在。
证明:当 时, -CDM不存在,由引理1,型为35的5-SCGDD不存在;由引理1、5和推论1,当 或t是偶数时,型为t5的5-SCGDD不存在;当t是奇数且 以及 ,p为素数, 或 时,由引理1、4可知,型为t5的5-SCGDD存在。下面只需考虑 , ,其中 , 是素数的情况。由引理1、4,存在型为 的5-SCGDD和型为 的5-SCGDD,再由构造法1,型为 的5-SCGDD存在。综上,结论得证。
定理3 当t为奇数, 或9p, 为素数且 , , 时,型为tr的5-SCGDD存在。
证明:由引理3,当 且 时,B 存在;又由定理2,当t是奇数, 或9p, 是素数且 时,型为t5的5-SCGDD存在;再利用构造法2,结论得证。
由引理2、6及定理3易得下面结论。
推论2 当 满足下列条件之一时,型为tr的5-SCGDD存在:
1) ;
2) 或45, 是素数。
推论3 当 为奇数, 或9p, 为素数且 ,t和r取值为以下情况时,型为 的5-SCGDD存在:
1) , 且 ;
2) , 是素数且 , ;
3) , 是素数或 ;
4) , ;
5) , 是素数或 , 和5q;
6) , 是素数, ;
7) , 是素数。
证明:利用构造法1,结合引理2、6和定理2,结论得证。
4. 小结
本文先确定了型为tr的区组长度为5的半循环可分组设计存在的必要条件,再根据已知的辅助设计,如循环差阵,t-正则循环填充的部分存在条件及两个递归构造方法,给出型为tr的5-SCGDD存在的若干充分条件,即得到了此半循环可分组设计的无穷类,所得结果对半循环可分组设计及带有AM-OPPTS/PW限制的光正交码的研究工作有一定的理论参考价值。
基金项目
国家自然科学基金青年基金项目(11401326);无穷维哈密顿系统及其算法应用教育部重点实验室开放课题(2023KFZR03);内蒙古自治区高等学校科学研究项目(NJZY19021,NJZY22599,NJZY22600)。
文章引用
杜 珺,黄月梅. 型为tr的5-半循环可分组设计
Semi-Cyclic Group Divisible Design of Type tr with Block Size 5[J]. 理论数学, 2024, 14(01): 335-340. https://doi.org/10.12677/PM.2024.141034
参考文献
- 1. Yin, J.X. (2002) A General Construction for Optimal Cyclic Packing Designs. Journal of Combinatorial Theory (Series A), 97, 272-284. https://doi.org/10.1006/jcta.2001.3215
- 2. Gallant, R.P., Jiang, Z. and Ling, A.C.H. (1999) The Spectrum of Cyclic Group Divisible Designs with Block Size Three. Journal of Combinatorial Design, 7, 95-105. https://doi.org/10.1002/(SICI)1520-6610(1999)7:2%3C95::AID-JCD2%3E3.0.CO;2-K
- 3. Wang, J.M. and Yin, J.X. (2010) Two-Dimensional Optical Orthogonal Codes and Semicyclic Group Divisible Designs. IEEE Transactions on Information Theory, 56, 2177-2187. https://doi.org/10.1109/TIT.2010.2043772
- 4. Wang, K. and Wang, J.M. (2012) Semicyclic 4-GDDs and Related Two-Dimensional Optical Orthogonal Codes. Designs, Codes and Cryptog-raphy, 63, 305-319. https://doi.org/10.1007/s10623-011-9556-3
- 5. Wang, L.D., Feng, T., Li, Y.T., et al. (2023) Construction for Multichannel Conflict-Avoiding Codes with AM-OPPTS Restriction. IEEE Transactions on Infor-mation Theory, 69, 7398-7413. https://doi.org/10.1109/TIT.2023.3299307
- 6. Ge, G.N. and Yin, J.X. (2001) Constructions for Optimal Optical Orthogonal Codes. IEEE Transactions on Information Theory, 47, 2998-3004. https://doi.org/10.1109/18.959278
- 7. Hanani, H. (1975) Balanced Incomplete Block Designs and Related Designs. Discrete Mathematics, 11, 255-369. https://doi.org/10.1016/0012-365X(75)90040-0
- 8. Pan, R., Abel, R.J.R., Bunjamin, Y.A., et al. (2022) Differ-ence Matrices with Five Rows over Finite Abelian Groups. Designs, Codes and Cryptography, 90, 367-386. https://doi.org/10.1007/s10623-021-00981-6
- 9. Ge, G.N. (2005) On -Difference Matrices. Discrete Mathematics, 301, 164-174. https://doi.org/10.1016/j.disc.2005.07.004
- 10. Yin, J.X. (1998) Some Combinatorial Constructions for Optical Orthogonal Codes. Discrete Mathematics, 185, 201-219. https://doi.org/10.1016/S0012-365X(97)00172-6
- 11. Chang, Y.X. and Ji, L.J. (2004) Optimal Opti-cal Orthogonal Codes. Journal of Combinatorial Designs, 12, 346-361. https://doi.org/10.1002/jcd.20011
- 12. Ma, S. and Chang, Y.X. (2004) A New Class of Optimal Optical Orthogonal Codes with Weight Five. IEEE Transactions on Information Theory, 50, 1848-1850. https://doi.org/10.1109/TIT.2004.831845
- 13. Ma, S. and Chang, Y.X. (2005) Constructions of Optimal Optical Orthogonal Codes with Weight Five. Journal of Combinatorial Designs, 13, 54-69. https://doi.org/10.1002/jcd.20022
NOTES
*通讯作者。