Advances in Applied Mathematics
Vol.
12
No.
03
(
2023
), Article ID:
62980
,
15
pages
10.12677/AAM.2023.123119
低阶富勒烯图的匹配强迫谱和反强迫谱的 连续性
韩慧,周玉玉,王彦通*
西北师范大学数学与统计学院,甘肃 兰州
收稿日期:2023年2月21日;录用日期:2023年3月16日;发布日期:2023年3月23日

摘要
富勒烯图的凯库勒结构的内、外自由度,对应于图的完美匹配的强迫数与反强迫数,可用于衡量化学分子的稳定性。由于使用穷举法计算比较大的分子图给定完美匹配的反强迫数时过于耗时,因此本文选用相对高效的整数线性规划法计算了 的所有3958个同分异构体的匹配强迫谱和反强迫谱,据此给出了它们的连续性,并将相应的结果汇总成了一系列表格和折线图。本文的工作将为富勒烯图的稳定性等研究提供一些理论参考。
关键词
富勒烯图,强迫谱,反强迫谱,整数线性规划,连续性

Continuity of Matching Forcing Spectra and Anti-Forcing Spectra for Lower-Order Fullerenes
Hui Han, Yuyu Zhou, Yantong Wang*
College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu
Received: Feb. 21st, 2023; accepted: Mar. 16th, 2023; published: Mar. 23rd, 2023

ABSTRACT
The innate and external degrees of freedom of the Kekulé structure of fullerenes, corresponding to the forcing number and anti-forcing number of the perfect matching of graphs, can be used as a measure of molecular stability. The exhaustive method is too time-consuming to calculate the anti-forcing number of the perfect matching of large graphs. Therefore, this paper uses efficient integer linear programming to calculate the forcing spectrum and anti-forcing spectrum of all 3958 isomers of , gives their continuity, and summarizes the results into a series of tables and line charts. The work presented in this paper will provide some theoretical references for studying the stability of fullerenes.
Keywords:Fullerene, Forcing Spectrum, Anti-Forcing Spectrum, Integer Linear Programming, Continuity

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近些年来,图的匹配在有机化学领域的应用尤为突出。图的完美匹配的强迫数与反强迫数等价于多环共轭分子的凯库勒结构的内、外自由度。1985年Randic和Klein [1] 第一次提出强迫数的概念,Harary等 [2] 在1991年研究六角系统的时候将其正式称为强迫数。2004年,Adams等 [3] 定义了图G的强迫谱 ,即图G的所有完美匹配的强迫数构成的集合。2010年,张和平等 [4] 证明了任意富勒烯图的每个完美匹配的强迫数均不小于3。
2007年,Vukiěević和Trinajstić [5] 提出了反强迫数的概念。图G的反强迫谱区间 的定义类似于强迫谱,即图G的所有完美匹配的反强迫数构成的集合。如果 是一个整数区间,则称图G的反强迫谱区间是连续的;类似地,若 是一个整数区间,则称图G的强迫谱是连续的。2007年,邓汉元 [6] 得到了链状六角系统的反强迫数的算法和反强迫数的上下界。2015年,杨琴和张和平等 [7] 证明了富勒烯图的反强迫数至少为4,并且给出了构造所有反强迫数为4的富勒烯图的程序,进而证明了26个顶点的所有富勒烯图的反强迫数都为5。王杰彬、韩振云、姚海元等 [8] [9] [10] 得出了梯子图及几类变形梯子图的反强迫细谱和反强迫谱的连续性。刘雨童、韩慧、王杰彬等 [11] 研究了Möbius梯状图 的反强迫谱。刘雨童、马聪聪、姚海元等 [12] [13] [14] 使用整数线性规划的方法计算了60阶等富勒烯图的强迫谱和反强迫数,并讨论其连续性。在此基础上,本文沿用他们的整数线性规划法,计算出了阶数不超过58的所有富勒烯图的强迫谱和反强迫谱,并得出了强迫谱和反强迫谱的连续性,同时给出了阶数不超过58的富勒烯图的所有同分异构体所对应的强迫谱(反强迫谱)构成的表格。
2. 预备知识
有限的简单图G是指一个有序的二元组 ,其中 表示图G的顶点集, 表示图G的边集。图G的一个边子集M称为G的一个匹配,如果M中任意两条边均不相邻,则称M中边为G的匹配边。若存在M中的边与v相邻,则称M饱和顶点v,并且称v是M饱和的,否则称v是M非饱和的。若G的每个顶点都是M饱和的,则称M是G的完美匹配。即G的完美匹配是覆盖G的所有顶点的不相邻边的集合。
设M是图G的一个完美匹配,称G的圈C是M-交错圈,若圈C的边交替的出现在M和 中。若M的子集S不包含在G的其他完美匹配中,则称S为M的强迫集。M的强迫数是指M的最小强迫集的大小,记作 。图G中所有完美匹配强迫数的最小值称为G的(最小)强迫数,记作 ; 而最大值称为G的最大强迫数,记作 。
设 ,若M是 中唯一的完美匹配,则称S'为M的反强迫集,其中 表示从图G中删除集合S'中的所有边后剩余的支撑子图。M的反强迫数是指M的最小反强迫集的大小,记作 。类似地,将图G中所有完美匹配反强迫数的最小值称为G的(最小)反强迫数,记作 ;而最大值称为G的反最大强迫数,记作 。
关于图的完美匹配的强迫集和反强迫集有如下刻画。
引理1 [3] [15] [16] 设M为图G的一个完美匹配,则
1) 是M的强迫集当且仅当S包含G的每个M-交错圈的至少一条(匹配)边。
2) 是M的反强迫集当且仅当S'包含图G的每个M-交错圈的至少一条(非匹配)边。
3. 整数线性规划法
由于本文需要通过整数线性规划法计算出富勒烯图的强迫谱和反强迫谱,因此下面简单介绍整数线性规划法的原理。该方法由姚海元、马聪聪、刘雨童等 [12] [13] [14] 给出。
通过引理1,可将寻找最小强迫集 优化为问题:S是包含每个M-交错圈的至少一条(匹配)边的最小边子集。进而,得到图G的一个完美匹配M的强迫数的方法如下:
首先,给图G的顶点和边标号,其次生成图G的所有完美匹配(本文所使用的完美匹配是利用C程序生成的,此程序是在曾令辉的程序的基础上稍作修改得到的),再将每个完美匹配依次与其他完美匹配作对称差,得到该完美匹配的所有M-交错圈(即作对称差得到的连通分支)。若G有l个M-交错圈,令 是一个 矩阵,它的每个行向量对应于一个M-交错圈的0-1关联向量,其中交错圈上匹配边的位置为1,非匹配边的位置为0。令b和c为全1列向量,其中b的维数为l,c的维数为n。最后,我们就有了下面的整数线性规划(ILP):
(ILP):
s.t.
注释:M的强迫数就是上述(ILP)的最优值,若想得到M的反强迫数,只需在构造矩阵 时将交错圈上匹配边的位置改为0,非匹配边的位置改为1即可。
4. 低阶富勒烯图的强迫谱和反强迫谱及其连续性
本文对阶数不超过58的富勒烯图的所有3958个同分异构体进行了编号,其中48阶及以内的富勒烯图的同分异构体的数目、编号和邻接关系是通过Mathematica软件的数据库直接得到的,50阶到58阶的富勒烯图的同分异构体的数目、编号和邻接关系是从一个关于富勒烯的网站https://hog.grinvin.org/Fullerenes上得到的(见图1)。
定理1 的所有3958个同分异构体的强迫谱都是连续的。
定理2在 的所有3958个同分异构体中有3849个同分异构体的反强迫谱是连续的。
定理3在 的所有3958个同分异构体中有109个的反强迫谱是不连续的。其中次小不连续的有8个,次大不连续的有101个。
下面我们以C54为例,令 为C54的第i个同分异构体,[]表示连续的整数区间,{ }U[ ]表示次小整数不连续的整数区间,[ ]U{ }表示次大整数不连续的整数区间。
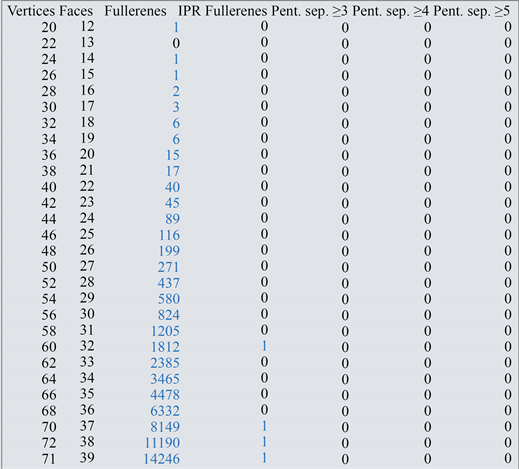
Figure 1. Low-order fullerenes
图1. 低阶富勒烯图(数据来源:https://hog.grinvin.org/Fullerenes)
由整数线性规划法我们可以得到C54所有同分异构体的强迫谱和反强迫谱。例如通过整数线性规划法我们可以计算出 的每一个完美匹配的强迫数和反强迫数,并得出 的强迫谱为连续的整数区间[4, 7],反强迫谱为次大反强迫数不连续的整数区间[6, 12] U {14}。类似的我们可以得到C54的其他同分异构体的强迫谱和反强迫谱。
对C54的同分异构体中强迫谱(反强迫谱)相同的同分异构体编号进行统计,得到:
1. 具有相同强迫谱的C54的同分异构体编号如下:
强迫谱为[3, 6]的有9个同分异构体,编号为:127,129,205,304,403,460,500,505,559。
强迫谱为[3, 7]的有245个同分异构体,编号为:2,4,9,12,14,21,22,23,24,25,26,28,29,30,31,32,34,36,39,43,44,45,46,47,48,51,58,60,62,63,64,66,67,68,69,70,71,72,78,79,80,83,84,88,89,90,92,96,98,99,100,101,104,105,106,109,113,115,118,121,122,123,124,125,126,128,132,134,135,136,137,139,141,142,143,144,145,146,147,148,155,156,158,159,160,161,162,165,167,170,173,174,183,188,190,191,192,196,199,200,201,203,204,206,207,208,209,218,219,220,222,223,224,225,226,227,228,229,230,231,232,234,237,238,239,240,241,242,244,245,248,249,254,256,257,258,259,261,262,263,264,267,276,277,281,283,284,285,287,288,289,290,293,294,295,296,297,298299,300,301,302,305,306,308,309,312,314,316,323,324,325,327,328,335,338,340,341,346,349,350,351,356,357,358,359,361,362,363,365,367,374,375,377,379,380,382,383,387,395,397,400,401,402,404,406,407,430,431,432,433,438,440,442,455,456,457,462,464,466,471,472,476,478,481,494,495,497,498,503,512,516,517,518,519,521,523,526,531,543,546,548,554,561。
强迫谱为[3, 8]的有11个同分异构体,编号为:7,10,11,13,27,59,61,74,91,116,119。
强迫谱为[4, 6]的有12个同分异构体,编号为:166,268,405,411,469,506,511,524,527,529,542,544。
强迫谱为[4, 7]的有284个同分异构体,编号为:1,3,5,6,8,15,16,17,18,19,20,33,35,37,38,40,41,42,49,50,52,53,54,55,57,65,73,75,76,77,81,82,85,86,87,93,94,95,97,102,103,107,108,110,112,114,117,120,130,131,133,138,140,149,150,151,152,153,154,157,163,164,168,169,171,172,175,176,177,178,179,180,181,182,184,185,186,187,189,193,194,195,197,198,202,210,211,213,214,215,216,217,233,235,236,243,246,247,250,251,252,253,255,260,265,266,269,270,271,272,273,274,275,278,279,280,282,291,292,303,307,310,311,313,315,317,319,320,321,322,326,329,330,331,332,333,334,336,337,339,342,343,344,345,347,348,352,353,354,355,360,364,366,368,369,373,376,378,381,384,385,386,388,389,390,391,392,393,396,399,408,409,412,413,414,415,418,419,420,421,422,423,424,425,426,427,428,429,434,436,437,439,441,443,444,445,446,447,448,449,450,451,452,453,454,458,459,461,463,465,467,468,470,473,474,475,477,480,482,483,484,485,486,487,488,489,490,491,492,493,496,499,501,502,504,507,508,509,510,513,514,515,520,522,525,528,530,532,533,534,535,536,537,538,539,540,541,545,547,549,550,551,552,553,555,556,557,558,560,562,563,564,565,567,568,570,571,572,573,574,575,576,577,578。
强迫谱为[4, 8]的有19个同分异构体,编号为:56,111,212,221,318,370,371,372,394,398,410,416,417,435,479,566,569,579,580。
对上述编号进行统计,得出C54的所有580个同分异构体所对应的强迫谱区间构成的表格,其中C54的强迫谱上界分别为6,7,8,强迫谱下界分别为3,4,它们构成了6个不同的连续强迫谱区间:
注:表中数据表示的是每个强迫谱区间的同分异构体个数。
C20,C24,C26均只有1个同分异构体,强迫谱分别为{3},[2, 3],{3},C30的3个同分异构体的强迫谱均为[3, 4],C32的6个同分异构体的强迫谱均为[3, 4],由于它们都只有一个强迫谱区间,故不做成表格。
由上述方法我们可以得到:
1) 构成2个不同的连续强迫谱区间的表格如下:
C28:
C34:
C36:
C38:
C42:
2) 构成3个不同的连续强迫谱区间的表格如下:
C40:
3) 构成4个不同的连续强迫谱区间的表格如下:
C44:
C48:
C50:
4) 构成5个不同的连续强迫谱区间的表格如下:
C46:
C52:
C56:
C58:
2. 具有相同反强迫谱的C54的同分异构体编号如下:
反强迫谱为{4} U [6, 12]的有1个同分异构体,编号为:45。
反强迫谱为[5, 12]的有9个同分异构体,编号为:46,70,102,107,127,231,290,301,505。
反强迫谱为[5, 13]的有25个同分异构体,编号为:1,7,12,13,14,25,30,43,44,47,58,68,96,99,104,106,108,230,264,267,288,289,292,299,395。
反强迫谱为[5, 14]的有7个同分异构体,编号为:31,77,82,87,112,145,190。
反强迫谱为[6, 11]的有2个同分异构体,编号为:411,469。
反强迫谱为[6, 12]的有149个同分异构体,编号为:18,35,39,55,100,121,122,124,128,129,132,135,136,140,141,142,149,152,153,158,166,174,191,200,204,205,208,223,224,227,229,232,235,237,239,241,248,250,255,256,257,260,268,269,271,272,282,284,295,296,300,303,304,314,321,324,331,337,341,345,351,354,356,357,359,362,364,371,373,378,379,381,392,396,402,403,404,405,406,408,419,422,431,440,441,442,443,455,459,460,463,467,470,472,475,482,484,485,488,493,498,500,501,502,508,510,511,512,513,514,516,518,519,521,523,524,,525,526,528,530,531,534,535,538,542,544,545,546,548,550,551,553,558,559,562,563,564,566,568,569,571,573,574,575,576,577,578,579,580。
反强迫谱为[6, 13]的有295个同分异构体,编号为:4,5,9,15,17,19,21,22,23,24,26,32,33,34,36,37,38,40,42,48,49,50,51,52,53,54,56,57,60,63,64,65,66,67,69,71,75,78,80,81,83,84,85,90,92,93,95,98,109,110,113,114,115,116,120,123,130,131,133,134,137,138,139,143,144,146,147,148,150,151,154,155,159,160,161,162,163,165,167,168,169,170,171,173,175,176,177,178,179,182,183,184,185,186,192,193,194,195,197,198,199,201,202,203,206,207,209,210,211,213,214,216,217,218,219,220,222,225,226,228,233,234,236,238,240,242,243,244,246,251,252,253,254,258,259,261,262,263,265,266,273,274,275,276,278,279,280,283,285,286,287,291,293,294,297,298,302,305,306,307,308,312,313,315,316,317,319,322,323,325,326,328,329,330,332,333,334,336,338,339,340,342,344,346,347,348,349,350,352,353,355,358,360,363,365,367,368,369,372,374,375,376,377,382,384,385,386,387,388,391,393,397,399,400,401,407,409,413,414,418,420,421,423,424,425,427,428,430,432,433,436,437,438,439,444,446,447,448,449,450,451,452,453,454,456,457,458,464,465,466,471,473,476,477,478,481,483,486,487,489,490,491,494,495,496,497,499,503,504,506,507,509,515,517,520,522,532,533,537,539,541,543,547,549,552,554,555,556,557,560,561,565,567,570,572。
反强迫谱为[6, 12] U {14}的有6个同分异构体,编号为:3,27,41,79,101,119。
反强迫谱为[6, 14]的有73个同分异构体,编号为:2,6,8,16,20,28,29,59,62,72,73,74,76,86,88,89,94,97,103,105,111,117,118,125,126,156,157,164,172,180,181,187,188,189,196,212,215,221,245,247,249,270,277,281,309,310,311,318,320,327,335,343,361,366,370,380,383,389,390,394,398,412,415,416,426,434,435,461,462,474,479,492,536。
反强迫谱为[6, 13] U {15}的有5个同分异构体,编号为:10,11,61,91,410。
反强迫谱为[7, 11]的有1个同分异构体,编号为:527。
反强迫谱为[7, 12]的有4个同分异构体,编号为:429,445,468,529。
反强迫谱为[7, 13]的有2个同分异构体,编号为:480,540。
反强迫谱为[7, 14]的有1个同分异构体,编号为:417。
对上述编号进行统计,得出C54的所有580个同分异构体所对应的反强迫谱区间构成的表格,其中C54的反强迫谱上界分别为11,12,13,14,15,反强迫谱下界分别为4,5,6,7,它们构成了13个不同的反强迫谱区间:
注:表中表示的是每个反强迫谱区间的同分异构体个数;*: 中的 分别表示次小反强迫数不连续的同分异构体个数,反强迫谱连续的同分异构体个数以及次大反强迫数不连续的同分异构体个数。
C20,C24,C26均只有1个同分异构体,它们的反强迫谱分别[4, 5],[4, 6],[5, 6],由于它们都只有一个反强迫谱区间,故不做成表格。
由上述方法我们可以得到:
1) 构成2个不同的连续反强迫谱区间的表格如下:
C28:
2) 构成3个不同的反强迫谱区间的表格如下:
C30:
C32:
C34:
C36:
3) 构成5个不同的反强迫谱区间的表格如下:
C38:
4) 构成6个不同的反强迫谱区间的表格如下:
C40:
C42:
5) 构成8个不同的反强迫谱区间的表格如下:
C46:
6) 构成9个不同的反强迫谱区间的表格如下:
C48:
7) 构成10个不同的反强迫谱区间的表格如下:
C44:
C50:
8) 构成11个不同的反强迫谱区间的表格如下:
C52:
9) 构成14个不同的反强迫谱区间的表格如下:
C58:
10) 构成15个不同的反强迫谱区间的表格如下:
C56:
由上述表格可分别得出 的最大强迫数、最小强迫数、最大反强迫数以及最小反强迫数,并据此绘制出如下两个分别反映这些富勒烯图的强迫数和反强迫数变化规律的折线图(见图2,图3)。由图可知,它们的最大强迫数和最大反强迫数是一条向上增长的曲线,而最小强迫数和最小反强迫数近似一条水平直线。

Figure 2. The trend of maximum and minimum forcing numbers in lower-order fullerenes
图2. 低阶富勒烯图的最大和最小强迫数变化趋势
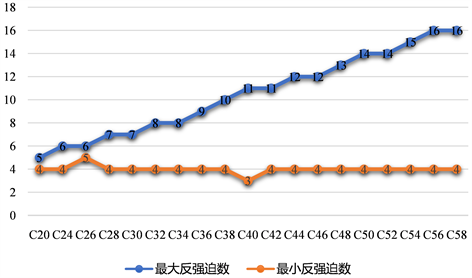
Figure 3. The trend of maximum and minimum anti-forcing numbers in lower-order fullerenes
图3. 低阶富勒烯图的最大和最小反强迫数变化趋势
基金项目
国家自然科学基金资助项目(12161081)。
文章引用
韩 慧,周玉玉,王彦通. 低阶富勒烯图的匹配强迫谱和反强迫谱的连续性
Continuity of Matching Forcing Spectra and Anti-Forcing Spectra for Lower-Order Fullerenes[J]. 应用数学进展, 2023, 12(03): 1173-1187. https://doi.org/10.12677/AAM.2023.123119
参考文献
- 1. Randić, M. and Klein, D.J. (1986) Kekulé Valence Structures Revisited. Innate Degrees of Freedom of π-Electron Cou-plings. In: Trinajstic, N., Ed., Mathematics and Computational Concepts in Chemistry, John Wiley & Sons, Inc., New York, 274-282.
- 2. Harary, F., Klein, D.J. and Živkovič, T.P. (1991) Graphical Properties of Polyhexes: Perfect Matching Vector and Forcing. Journal of Mathematical Chemistry, 6, 295-306. https://doi.org/10.1007/BF01192587
- 3. Adams, P., Mahdian, M. and Mahmoodian, E.S. (2004) On the Forced Matching Numbers of Bipartite Graphs. Discrete Mathematics, 281, 1-12. https://doi.org/10.1016/j.disc.2002.10.002
- 4. Zhang, H., Ye, D. and Shiu, W.C. (2010) Forcing Matching Num-bers of Fullerene Graphs. Discrete Applied Mathematics, 158, 573-582. https://doi.org/10.1016/j.dam.2009.10.013
- 5. Vukiěević, D. and Trinajstić, N. (2007) On the Anti-forcing Num-ber of Benzenoids. Journal of Mathematical Chemistry, 42, 575-583. https://doi.org/10.1007/s10910-006-9133-6
- 6. Deng, H. (2007) The Anti-Forcing Number of Hexagonal Chains. MATCH Communications in Mathematical and in Computer Chemistry, 58, 675-682.
- 7. Yang, Q., Zhang, H. and Lin, Y. (2015) On the Anti-Forcing Number of Fullerene Graphs. MATCH Communications in Mathematical and in Com-puter Chemistry, 74, 673-692.
- 8. 韩振云, 姚海元. 删边梯子图和“L”型梯子图的反强数[J]. 应用数学进展, 2019, 8(8): 1352-1361.
- 9. 姚海元, 王杰彬, 王旭. 循环梯状图的完美匹配的反强迫谱与卢卡斯数列[J]. 西北师范大学学报(自然科学版), 2018, 54(2): 21-25.
- 10. 王杰彬. 几类特殊图的反强迫谱的研究[D]: [硕士学位论文]. 兰州: 西北师范大学, 2018.
- 11. 刘雨童, 韩慧, 王杰彬. Möbius梯状图的完美匹配的反强迫多项式和卢卡斯数[J]. 应用数学进展, 2021, 10(8): 2868-2874.
- 12. 马聪聪. 几类富勒烯图的反强迫多项式[D]: [硕士学位论文]. 兰州: 西北师范大学, 2021.
- 13. 刘雨童. 60阶富勒烯图的双强迫多项式[D]: [硕士学位论文]. 兰州: 西北师范大学, 2022.
- 14. Liu, Y., Ma, C., Yao, H. and Wang, X. (2002) Computing the Forcing and Anti-Forcing Numbers of Perfect Matchings for Graphs by Integer Linear Programmings. MATCH Communications in Mathematical and in Computer Chemistry, 87, 561-575. https://doi.org/10.46793/match.87-3.561L
- 15. Riddle, M.E. (2002) The Min-imum Forcing Number for the Torus and Hypercube. Discrete Mathematics, 245, 283-292. https://doi.org/10.1016/S0012-365X(01)00228-X
- 16. Lei, H., Yeh, Y.-N. and Zhang, H. (2016) Anti-Forcing Numbers of Perfect Matchings of Graphs. Discrete Applied Mathematics, 202, 95-105. https://doi.org/10.1016/j.dam.2015.08.024
NOTES
*通讯作者。