Journal of Electrical Engineering
Vol.04 No.01(2016), Article ID:17077,8
pages
10.12677/JEE.2016.41004
Parameter Design of the Test Device for Arc Extinguishing
Xiaoling Zhao1, Juntao Jiao1, Su Zhao1, Dengming Xiao1, J. D. Yan2
1Department of Electrical Engineering, Shanghai Jiao Tong University, Shanghai
2University of Liverpool, Liverpool, UK

Received: Feb. 12th, 2016; accepted: Feb. 26th, 2016; published: Mar. 4th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Based on the mathematic theory for arc extinguishing, Mayr’s equation, we theoretically derived parameters of the test device for arc extinguishing, including the average speed of the contacts, size of nozzle, distance of the contacts, etc. Through qualitative analysis of elements and character parameters in arc extinguished chamber, as well as the experience of GCB design, mathematic theoretical calculation and arc extinguishing test, we came up with a tentative calculation and an estimation method for pressed arc extinguished chamber, which provide accordance for relative arc extinguishing test study.
Keywords:Test Device for Arc Extinguishing, Mayr’s Equation, Parameter Design

灭弧试验装置的参数设计
赵小令1,焦俊韬1,赵谡1,肖登明1,J. D. Yan2
1上海交通大学电气工程系,上海
2利物浦大学,利物浦,英国

收稿日期:2016年2月12日;录用日期:2016年2月26日;发布日期:2016年3月4日

摘 要
根据灭弧装置设计的数学理论依据麦也尔方程,本文较详细地进行了灭弧试验装置各项参数计算方法的介绍,包括平均分闸速度、喷嘴、触头开距等。通过对灭弧室各元件及各种特性参数的定性分析,并结合以往GCB (Gas Circuit Breaker)新品设计、灭弧室数学模拟计算及开断试验的经验,本文提出了一套压气式灭弧室初步设计及估算方法,为研制相关灭弧试验装置提供必要参考。
关键词 :灭弧试验装置,麦也尔方程,参数计算

1. 引言
自彼得罗夫于 1803 年发现电弧至今已有100年时间,然而关于电弧的研究是不多的,并且大都集中在人工照明方面利用电弧的应用上[1] 。长期以来,开断电器中的电弧研究集中在交流电弧电流过零阶段物理过程的研究。当断路器开断时,只要电路中的电流超过上百毫安,电源电压超过几十伏,动、静触头间就会出现电弧。此时触头即使已经分开,电流依然通过触头间的电弧继续流通,直到触头分开到足够长的距离,电弧熄灭后,电路才真正开断[2] -[4] 。因此,电弧是高压断路器开断过程中几乎不可避免的现象。而灭弧试验对新的灭弧介质、断路器结构和设备改进都有重要意义,在对电弧和设备的研究中起着举足轻重的作用。在灭弧实验前,对相关装置参数的估算和选择也是实验前必须的步骤。
气吹式(self-blast)断路器是一种常见的断路器结构。其在触头分开关断电路时,会有灭弧气体从高压区流向低压区吹拂电弧,从而达到灭弧的作用[5] 。气吹式断路器适合电路能量大,损耗少,电弧形成时间长的灭弧试验。同时,没有气体吹拂电弧时,这种灭弧试验装置还可以进行静态灭弧试验[6] ,此时用静态气体对电弧直接达到散热作用。适合电路能量较少、损耗较大,电弧形成时间较短的灭弧试验。
本文介绍了灭弧装置设计的数学理论依据麦也尔方程,并计算了灭弧试验装置的各项参数,包括平均分闸速度、喷嘴,触头开距等,为研制相关灭弧试验装置提供必要参考。
2. 参数设计的数学理论依据
灭弧装置设计的数学理论依据是麦也尔方程[7] 。麦也尔所采用的方法适合于交流过零时的情况。麦也尔主要假设电弧散热功率N取作常数,并把电弧电导gh与电弧内积存的热量Q的函数写为
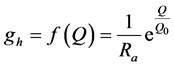 (1)
(1)
因此
 (2)
(2)
其中,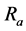 是常数(欧),
是常数(欧), 是常数(瓦∙秒),它与电弧热容有关。
是常数(瓦∙秒),它与电弧热容有关。
电弧微分方程式为
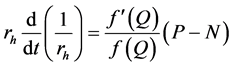 (3)
(3)
其中, 是电弧电阻,t是时间,P是电弧功率,N是电弧散热功率。将式(1) (2)带入电弧的微分方程式
是电弧电阻,t是时间,P是电弧功率,N是电弧散热功率。将式(1) (2)带入电弧的微分方程式
 (4)
(4)
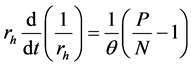 (5)
(5)
式中,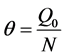 (秒),被称为电弧时间常数。电弧功率可写成
(秒),被称为电弧时间常数。电弧功率可写成
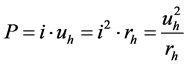 (6)
(6)
带入式(5)得
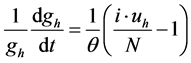 (7)
(7)
和
 (8)
(8)
式中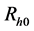 为t = 0时的电弧电阻。
为t = 0时的电弧电阻。
当电弧电流i为已知时,利用式(8)可以求出rh的变化过程。将式(6)代入(5),得
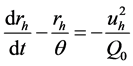 (9)
(9)
解得
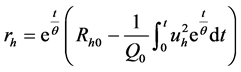 (10)
(10)
由式(10),以及弧上电压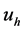 ,就可以求出
,就可以求出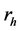 的变化过程。
的变化过程。
若已知电弧电流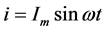 ,且
,且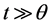 ,从式(8)得
,从式(8)得
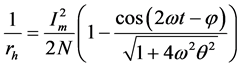 (11)
(11)
式中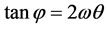 。当
。当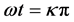 ,也就是电流过零时,电弧电阻r0由式(5)可得,当
,也就是电流过零时,电弧电阻r0由式(5)可得,当 时
时
 (12)
(12)
可见,增加弧隙散能系数N,或减小电弧时间常数θ,都能使电流过零时的电弧电阻r0增加。电流过零后,介质的恢复强度uj可求得
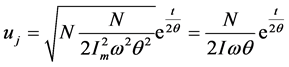 (13)
(13)
由式(13)可知,时间常数θ对介质强度uj有直接影响。一种灭弧介质或灭弧装置的θ越小,表明灭弧能力越强。因此,电弧时间常数θ是衡量灭弧能力的一个重要指标。当灭弧方式与灭弧装置不同的时候,θ值也不同[8] [9] 。
3. 灭弧试验装置的设计
本文把灭弧试验装置当做气体断路器(GCB)来进行设计。而 GCB 灭弧室带负荷开断过程是一个涉及热力学、电磁学、气体动力学及高压绝缘等专业等发面的极其复杂的物理过程,电弧的燃烧与熄灭特性与灭弧室结构是息息相关的[10] 。以往灭弧室的设计是以理论定性分析为基础,同时结合研究实验的经验设计,设计可靠性小,盲目性大、成功率低。近年来,灭弧室开断特性的数学模拟计算软件包[11] 已开发成功,给GCB新品设计开发工作带来了新的方法。然而,新的GCB灭弧室数学计算模型或新型灭弧室研究试品设计的好坏,对计算机计算结果的适用性及反复修改设计、反复计算的次数都有重要影响。
本节对灭弧室各元件及各种特性参数做了定性分析,结合以往GCB新品设计、灭弧室数学模拟计算和开断试验的经验,提出了一套压气式灭弧室初步设计及估算方法。这有助于快速而比较准确地建立一个新灭弧室数学计算模型或新品灭弧室研究实验方案,这个步骤对于减少灭弧室数学模拟计算次数和研究试验次数有重要意义[12] 。
影响灭弧室工作特性的主要元件和特性参数有:分闸速度;行程、超程和开距;压气缸直径和容积;喷嘴尺寸与形状;触头形状与尺寸等[13] [14] 。
考虑到灭弧试验装置要为后续关断大电流试验做必要准备,设计按照关断大短路电流而设计。特此假定试验电压为6 kV左右,试验电流为300 A左右,试验气压为0.2 MPa左右。现根据设计要求对灭弧装置各参数和元件的设计要点分析如下。
3.1. 平均分闸速度vf的设计
确定vf主要考虑两个因素:一是开断小电容电流(相当于冷态开断)时,要保证断口有足够的介质恢复速度;二是近区故障(SLF)开断时,对应短燃弧时间tad,要保证断口有足够快的介质热恢复速度。
切空载长线GCB开断小电容电流(31.5~500 A)时,对应于最短燃弧时间的断口电强度可由下式计算
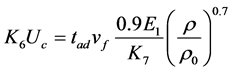 (14)
(14)
其中,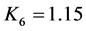 是设计裕度,
是设计裕度,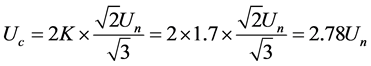 ,为恢复电压峰值(kV)。
,为恢复电压峰值(kV)。
根据JB5871-1991《交流高压断路器线路充电电流开合试验》表4和第11.2.2条的相关规定,单相试验时恢复电压峰值为:

式中,k = 1.2 - 1.7,该系数取决于系统中性点是否接地、是否发生单相(或两相)短路,计算时取最大值1.7。Un为系统额定工作电压。
tak (ms)是从起弧瞬时到恢复电压上升到峰值所需要的最短时间,即:
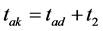
其中,tad是切小电容电流时可能的最短燃弧时间。参照部分产品的试验情况,与电压等级有一定关系的tad值列于如表1中。
表1中, (JB5871-1991规定值)。
(JB5871-1991规定值)。
E1 (kV/mm)为GCB在SF6操作闭锁气压时允许的雷电冲击场强。由于开断小电容电流时少量电弧分解物对绝缘有影响,计算时灭弧室断口间允许场强取0.9E1。
K7为断口电场分布不均匀系数,它与触头结构和开距有关。在切小电容电流开距较小时,K7值较大,参照部分产品电场数值计算的经验数据,K7推荐按如表2取值。
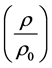 为切小电容电流时短燃弧时间对应的断口间SF6平均密度
为切小电容电流时短燃弧时间对应的断口间SF6平均密度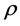 与GCB额定SF6密度
与GCB额定SF6密度 。不同灭弧室,
。不同灭弧室,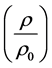 值不尽相同,根据部分灭弧室冷态气流场计算的经验数据,初步设计时可取
值不尽相同,根据部分灭弧室冷态气流场计算的经验数据,初步设计时可取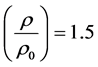 ,
,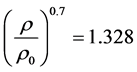 。
。
由下式(15)
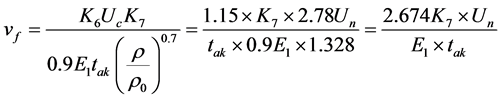 (15)
(15)
其中,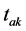 按表1取值(ms);
按表1取值(ms); 按表2取值;
按表2取值;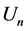 为额定电压(kV);
为额定电压(kV);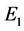 按表3取值。
按表3取值。
式(15)中,取 ,
, ,
,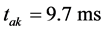 ,
,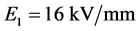 ,得到
,得到 。
。
3.2. 触头开距lk的设计
触头开距与分闸位置时断口间的静态耐受电压能力有关,同时也与开断时必需的熄弧距离有关。
相关设计时,需要考虑由vf及各种开断时预期的最长燃弧时间tac所决定的最长熄弧距离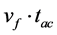 的需要,开距lk应满足下式要求
的需要,开距lk应满足下式要求
 (16)
(16)
同时还应按下式核算分闸位置时的静态电强度
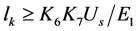 (17)
(17)
其中,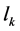 为触头开距(mm);
为触头开距(mm);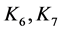 见式(15)和表2;
见式(15)和表2; 是比较稳妥的预期长燃弧时间;
是比较稳妥的预期长燃弧时间;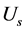 断口间雷电冲击耐受电压(计入反向电压峰值) (kV);
断口间雷电冲击耐受电压(计入反向电压峰值) (kV); 同式(15)值。
同式(15)值。
Table 1. The shortest extinguishing time tad for arc in long lines
表1. 切长线时可能的最短熄弧时间tad
Table 2. Electrical field uniformity K7 in arc extinguishing chamber
表2. 灭弧室断口电场不均匀系数K7
Table 3. Reference value in designing smooth conductors at different gas pressures in SF6 gas
表3. 不同SF6气压时光洁导体场强设计基准值
取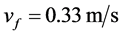 ,
,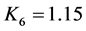 ,
,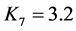 ,
,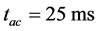 ,带入得
,带入得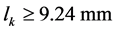 ,考虑需要一定的裕量,
,考虑需要一定的裕量, 。
。
此处的雷电冲击耐受电压其实是相对室外的断路器而言的,对于这个试验装置的设计本身基本是没有意义的,所以可以忽略这条设计标准。
3.3. 喷嘴设计
喷嘴形状和尺寸对气吹压力的建立和整个熄弧过程中气吹压力特性、弧道气流状态的影响都很大,对灭弧室的开断性能起着关键性作用。喷嘴的初步设计包括三个部分的形状和尺寸设计,即上游区设计、喉颈部及下游区。
1) 上游区设计
喷嘴入口处电弧的长度Lu对灭弧有两种相反的影响。适当而必要的入口电弧长度Lu有利于利用电弧能量来加热气缸的气体并使其增压,既有利于熄弧,也可减轻操动机构的负担。但若Lu太长,上游区的电弧能量和导电粒子积累过多,气流径向分速度下降(不利于弧根冷却),将影响电流过零后介质恢复速度的增长,对熄弧不利。
从定性分析入手,以部分产品的设计与开断试验经验为依据,Lu有三种定量的方法:
a) 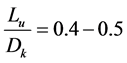
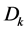 为喷嘴喉颈部直径,对应的喉部截面积
为喷嘴喉颈部直径,对应的喉部截面积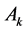 。
。
b) 
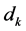 是触头外径。
是触头外径。
c) 气流入口侧表面积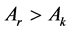 或
或
以上三种定量尺度中,尤其是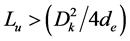 必须保证,
必须保证,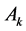 为喷嘴喉颈截面积。上游区气流通道(环形截面积
为喷嘴喉颈截面积。上游区气流通道(环形截面积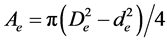 )设计对喷嘴气流特性及气缸压力特性都有重要影响。
)设计对喷嘴气流特性及气缸压力特性都有重要影响。
根据以往开断试验的经验,推荐按下式确定上游环形截面积 。
。
 (18)
(18)
 (19)
(19)
2) 喷嘴喉径Dk的设计
对于压气式灭弧室,Dk (mm)可按下式确定
 (20)
(20)
开断电流较小时,取较大的系数;开断电流较大时,取较小的系数。
按式(20)初步估算的Dk,还应通过灭弧室其他参数(如气缸直径、静弧触头直径)的选配之后才能确定。喉径与静弧触头之间隙Dk − dk常取3 mm左右。
3) 喉颈部的长度设计
喷嘴喉颈部的长度Lh及上游区的长度Lh是决定触头堵塞喷口时间的一个重要因素,堵塞时间td (ms)估算为
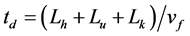
其中,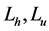 为喉颈及上游区长度(mm);
为喉颈及上游区长度(mm);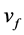 为平均分闸速度(m/s)。按照通常的设计经验,取td = 10 - 12 ms。当Lh、vf、Lu确定后,可按式(3)~(20)计算出Lk。
为平均分闸速度(m/s)。按照通常的设计经验,取td = 10 - 12 ms。当Lh、vf、Lu确定后,可按式(3)~(20)计算出Lk。
3.4. 触头设计
触头部分的设计,因为要配合喷嘴的设计,所以其实在喷嘴设计出来之后,触头的尺寸就大致定型了。取动触头直径为7 mm,静触头的直径为10 mm。之所以这样设计,一个是受制于喷嘴喉颈的大小,不得不让动触头直径小于8 mm,而静触头这样设计有效增大了动静触头的接触表面积,防止动静、触头之间虚接触。
由于预想的拉弧时间为微秒级,所以触头的发热情况可以忽略不计。因此触头材料为铜。
3.5. 灭弧室尺寸设计
灭弧室分为上游区和下游区两部分。上游区存储压缩气体,下游区为真空或正常大气压。
为了确保0.2 MPa的压力,上游区容积越大,需要的灭弧气体量越多。吹弧气流维持时间越长。
下游区容积越大,则上下游灭弧室压力差能维持更长时间,气流速度减小缓慢。
由于预想中灭弧时间比较短,因此对上下游灭弧室容积的大小要求并不苛刻。在实际制造过程中,灭弧室以有机玻璃圆筒为材料。灭弧室的大小以现成有机玻璃圆筒材料的尺寸而定。
4. 总语
本文根据断路器吹弧的气体动力学原理、上下游所需的压力差等理论,提出了灭弧试验所需要的实验装置的一些基本预期要求,根据这些要求,以标准SF6气体断路器(GCB)设计标准为参考,详细计算了灭弧试验装置的规格参数,为研制相关灭弧试验装置提供必要参考。
文章引用
赵小令,焦俊韬,赵 谡,肖登明,J. D. Yan. 灭弧试验装置的参数设计
Parameter Design of the Test Device for Arc Extinguishing[J]. 电气工程, 2016, 04(01): 23-30. http://dx.doi.org/10.12677/JEE.2016.41004
参考文献 (References)
- 1. 清华大学, 西安交通大学. 高电压绝缘[M]. 北京: 电力工业出版社, 1980.
- 2. 邱毓昌. GIS装置极其绝缘技术[M]. 北京: 水利电力出版社, 1994.
- 3. Christophorou, L.G. and Olthoff, J.K. (2000) Electron Interactions with SF6. Journal of Physical and Chemical Reference Data, 29, 267-330. http://dx.doi.org/10.1063/1.1288407
- 4. 李慧芬. SF6气体替代面临诸多挑战[J]. 高电压技术, 2000, 26(3): 50-51.
- 5. Qiu, Y. and Chalmers, I.D. (1993) Effect of Electrode Surface Roughness on Breakdown in SF6-N2 and SF6-CO2 Gas Mixtures. Journal of Physics D: Applied Physics, 26, 1928-1932. http://dx.doi.org/10.1088/0022-3727/26/11/014
- 6. Buttkau, A., Pfeiffer, J. and Sojka, B. (1984) Simens SF6/N2 Circuit-Breaker for Service at Low Temperature. Simens Power Engineering, 6, 32-37.
- 7. Christophorou, L.G., Olthoff, J.K. and Green, D.S. (1997) Gases for Electrical Insulation and Arc Interruption: Possible Present and Future Alternatives to SF6. Technical Note, 1425, 1-44.
- 8. Middleton, B. (2000) Cold Weather Applications of Gas Mixture (SF6/N2, SF6/CF4) Circuit Breakers: A User Utility’s Perspective. The US Environmental Protection Agency’s Conference on SF6 and the Environment: Emission Reduction Strategies, San Diego, 2-3 November 2000.
- 9. Pradayroly, C., Casanovasz, A.M., Hernouney, A. and Casanovasy, J. (1996) Spark decomposition of SF6 and SF6 + 50% CF4 Mixtures. Journal of Physics D: Applied Physics, 29, 1941-1951. http://dx.doi.org/10.1088/0022-3727/29/7/031
- 10. 肖登明, 邱毓昌, 李彦明. SF6混合气体中电子崩放电特性的研究[D]: [博士学位论文]. 西安: 西安交通大学, 1994.
- 11. 李正瀛. 电负性混合气体临界击穿场强与电子附着速率的探讨[J]. 物理学报, 1990, 39(9): 1400-1406.
- 12. Larin, A.V., Meurice, N., Trubnikov, D.N. and Vercauteren, D.P. (2004) Theoretical Analysis of the Synergism in the Dielectric Strength for SF6/CF4 Mixtures. Journal of Applied Physics, 96, 109-117. http://dx.doi.org/10.1063/1.1751637
- 13. Wu, C. and Kunhardt, E.E. (1988) Formulation and Propagation of Streamers in N2 and N2-SF6 Mixtures. Physical Review A, 37, 4396-4406. http://dx.doi.org/10.1103/PhysRevA.37.4396
- 14. Govinda Raju, G.R. and Dincer, M.S. (1982) Measurement of Ionization and Attachment Coefficients in SF6 and SF6 + N2. Journal of Applied Physics, 53, 8562-8567. http://dx.doi.org/10.1063/1.330502
