Pure Mathematics
Vol.4 No.06(2014), Article
ID:14365,5
pages
DOI:10.12677/PM.2014.46035
Boundedness of Solutions of a Second Order Differential Equation via Bellman’s Inequality
School of Science, Wuhan University of Science and Technology, Wuhan
Email: *645063914@qq.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Oct. 13th, 2014; revised: Oct. 31st, 2014; accepted: Nov. 4th, 2014
ABSTRACT
By using Bellman’s inequality, the boundedness of solutions of a second order differential equation is investigated. Two different forms of Bellman inequality are given, which can be used to get the boundedness of differential equations.
Keywords:Bellman Inequality, Differential Equation, Boundedness

基于Bellman不等式的一类二阶微分
方程的解的有界性
卢 明,王蔚敏*,吴 磊,刘少辉
武汉科技大学理学院,武汉
Email: *645063914@qq.com
收稿日期:2014年10月13日;修回日期:2014年10月31日;录用日期:2014年11月4日

摘 要
由Bellman不等式证明一类二阶微分方程的解的有界性,给出了两种不同形式的Bellman不等式,由此可得出有关微分方程解的有界性结论。
关键词
Bellman不等式,微分方程,有界性

1. 引言
早在1957年,欧阳亮在文[1] 中利用给出了如下引理:
若: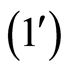




则

利用该引理,证明了 这类二阶微分方程的解的有界性,并给出了相关的结论。在2014年,Qusuay H. Alqifiary和Soon-Mo Jung在文[2] 中利用Bellman引理证明了一类二阶微分方程的Hyers-Ulam稳定性结论。而本文则是用Bellman引理1和引理5,在欧阳亮[1] 的基础上简化其证明过程,同时也减弱了文[1] 中对二阶微分方程的系数
这类二阶微分方程的解的有界性,并给出了相关的结论。在2014年,Qusuay H. Alqifiary和Soon-Mo Jung在文[2] 中利用Bellman引理证明了一类二阶微分方程的Hyers-Ulam稳定性结论。而本文则是用Bellman引理1和引理5,在欧阳亮[1] 的基础上简化其证明过程,同时也减弱了文[1] 中对二阶微分方程的系数 的要求,即只需要文[1] 中定理一中的条件(i)。除此之外,本文也与文[2] 中的定理2中对
的要求,即只需要文[1] 中定理一中的条件(i)。除此之外,本文也与文[2] 中的定理2中对 的要求不同,即不需要当
的要求不同,即不需要当 时,
时, 。从而对于证明微分方程的Hyers-Ulam稳定性起到了重要作用。
。从而对于证明微分方程的Hyers-Ulam稳定性起到了重要作用。
2. 正文
在本文中我们只讨论方程
 (1)
(1)
的解的有界性。
引理1 [2] :若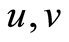 :
: 是可积函数,
是可积函数, 为常量且
为常量且![]() ,如果
,如果 满足不等式
满足不等式
 (2)
(2)
则
 (3)
(3)
证明:由(2)式可得
 (4)
(4)
对(4)式两边同时从0到 积分可得
积分可得
 (5)
(5)
整理可得
 (6)
(6)
综合(2)式可得
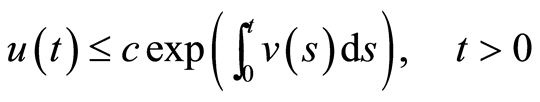 (7)
(7)
利用引理1,我们可以证明如下定理,即
定理2:若方程(1)的系数 ,
, 和
和 是可积函数,则当
是可积函数,则当 时,(1)式的所有解有界。
时,(1)式的所有解有界。
证明:对(1)式两边同乘 ,可得
,可得
 (8)
(8)
对(8)式从0到 积分并且利用分部积分可得
积分并且利用分部积分可得

 (9)
(9)
 (10)
(10)
令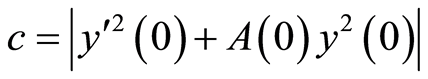 可得
可得
 (11)
(11)
那么
 (12)
(12)
对(12)进行变形可得
 (13)
(13)
利用引理1有
 (14)
(14)
即
 (15)
(15)
由于 为常量,
为常量, 也为一常量,故
也为一常量,故 。因而(1)式的解
。因而(1)式的解 是有界的。
是有界的。
我们来考虑方程
 (16)
(16)
利用上述的(15)式我们就可以得到如下的定理,即
定理3:若(16)满足条件![]() ,
,![]() 时,则当
时,则当 时,(16)的所有解有界。
时,(16)的所有解有界。
证明:令![]() ,那么由(15)式可得
,那么由(15)式可得
 (17)
(17)
这里的 。
。
引理4 [Biernacko]:若方程 的所有的解及其一阶微商有界,则方程
的所有的解及其一阶微商有界,则方程 的所有的解在条件
的所有的解在条件 时保持有界。
时保持有界。
引理5 [3] :若 ,
, 和
和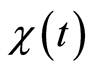 是定义在
是定义在 的实连续函数,
的实连续函数, 对所有的
对所有的 ,如果有不等式
,如果有不等式
 (18)
(18)
那么就有
 (19)
(19)
引理6:若 是可积函数,
是可积函数, 为常量且
为常量且![]() ,如果
,如果 满足不等式
满足不等式
 (20)
(20)
那么有
 (21)
(21)
证明:设![]() ,则
,则 。将上式带入(19)可得
。将上式带入(19)可得

根据数学分析中的young不等式可得
 (22)
(22)
令 ,根据引理5可得
,根据引理5可得
从而
 (23)
(23)
定理7:若方程
 (24)
(24)
满足下列条件
(i)![]() ,
,
(ii) 
则当 方程(21)所有的解保持有界。
方程(21)所有的解保持有界。
证明:显然我们只需证明(16)式的解的一阶微商在 时有界。给(16)式两边同乘
时有界。给(16)式两边同乘 ,再从0到
,再从0到 积分且利用分部积分可得:
积分且利用分部积分可得:
 (25)
(25)
因而
 (26)
(26)
由定理3以及引理5可得
 (27)
(27)
再根据引理4,一阶微商有界,就可以得到方程(24)是有界的。从而证得定理7成立。
定理8:若方程
 (28)
(28)
满足条件
 ,则当
,则当 时其所有的解保持有界。
时其所有的解保持有界。
证明:给(28)两边同乘 ,且从0到
,且从0到 积分,再利用分部积分,整理得
积分,再利用分部积分,整理得

则
 (29)
(29)
令
由引理1可得: 。从而可证得定理8。
。从而可证得定理8。
致 谢
本文是在冯育强教授的精心指导下完成的。从本科入学以来,无论在学习上还是在生活中冯老师都给予我们大量的关心,鼓励和帮助,对本文的写作进行悉心的指导,提出了宝贵的意见。在此,我们想冯老师表示深深的敬意和感谢!
基金项目
武汉科技大学优秀科技人才培育项目(2008RC01)武汉科技大学大学生科技创新项目(13ZRA067)。
参考文献 (References)
- [1] 欧阳亮 (1957) 有关分数阶微分方程的解的有界性. 数学进展, 3, 409-415.
- [2] Alqifiary, Q.H. and Jung, S.-M. (2014) On the Hyers-Ulam stability of differential equations of second order. Abstract and Applied Analysis, 2014, Article ID: 483707.

NOTES
*通讯作者。