Pure Mathematics
Vol.06 No.03(2016), Article ID:17376,6
pages
10.12677/PM.2016.63022
Computation of Distance-Based Topological Indices for Harary Graph H2m,n
Xingli Zhou, Wei Gao
School of Information, Yunnan Normal University, Kunming Yunnan

Received: Apr. 3rd, 2016; accepted: Apr. 18th, 2016; published: Apr. 21st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In the model of chemical graph theory, the molecular structure is represented as a graph: atoms represented by vertices and chemical bonds between atoms were expressed as edges. In this paper, we calculate the distance for each pair of vertex in Harary graph H2m,n by means of graph analysis, and then determine the expressions of Wiener related indices for Harary graph H2m,n according to the definition of topological indices.
Keywords:Harary Graph, Modified Wiener Index, Harary Index, Multiplicative Wiener Index

Harary图H2m,n的基于距离的拓扑指数计算
周兴丽,高炜
云南师范大学信息学院,云南 昆明

收稿日期:2016年4月3日;录用日期:2016年4月18日;发布日期:2016年4月21日

摘 要
化学图论其模型是用图结构来表示分子:原子用顶点来表示,原子之间的化学健用边来表示。本文利用图分析的方法计算Harary图H2m,n每对顶点的距离,并根据拓扑指数的定义给出维纳相关指数的表达式。
关键词 :Harary图,修改的维纳指数,Harary指数,乘法维纳指数

1. 引言
在化学图论和分子拓扑学中,对于不同的拓扑指数虽然可以用不同的方法计算得到,但其基本的思想及方法基础是一样的,那就是要确定原子的属性或分子图节点的化学特征(例如采用原子的分子连接度和原子共价半径等)、原子间的连接关系(键属性)以及利用各种分子图不变量(例如顶点数目、边数目、等长度路径数目、连接矩阵顶点度、分子图的特征多项式和图谱等) [1] 。
随着化学实验条件的改善和新化学生物技术的革新,大量的新化合物和药物涌现出来。近年来,有太多新发现的化合物、材料和药物急剧增长。这些新化学结构,都要鉴定它们的物理、化学和生物特征,这使得化学和制药领域的研究者的工作量大大增加。怎样才能精确、有效、快捷地知道新物质的特性成为现在科研的一个新的挑战。更多详细信息可以参看文献 [2] - [6] 。
研究实验表明:化合物和药物的部分特性离不开化学分子结构。所以,部分学者在分子结构图上定义了一些指标,如维纳指数,超维纳指数等,通过计算这些指数来得知它们的化学性质。这种方法可以大大减轻了鉴定药物特性的工作量,可以直接通过计算得出这些化学物质的特性,免去了化学实验,节约成本。关于指数信息可以参看文献 [7] - [14] 。
在理论化学中,其计算模型是用图结构来表示分子结构:其中原子用顶点来表示,原子之间的化学健用边来表示。一般地,设 是一个图,用顶点集合
是一个图,用顶点集合 即为原子集合,边集合
即为原子集合,边集合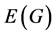 则为化学键集合。
则为化学键集合。
修改的维纳指数是原维纳指数的扩展,定义为
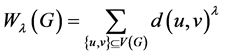 ,
,
其中 是非零实数。可见当
是非零实数。可见当 时,修改的维纳指数即为维纳指数。
时,修改的维纳指数即为维纳指数。
修改的超维纳指数是超维纳指数的扩展,定义为
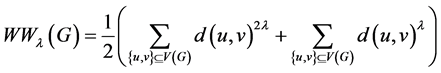 。
。
乘法维纳指数是维纳指数的另一种表现形式,定义为
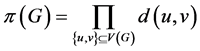 。
。
此外,对数乘法维纳指数定义为
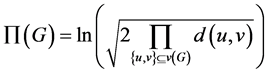
Harary指数是一类和维纳指数相关的指标,定义为
 =
=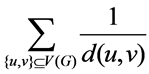 。
。
对应的Harary多项式则定义为
 。
。
上述Harary指数通常称为第一类Harary指数,而第二类和第三类Harary指数则定义为
 ,
,
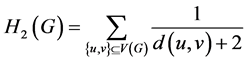 。
。
更一般地,广义Harary指数则定义为
 ,
,
其中 是一个非负整数。
是一个非负整数。
用 来表示Harary图,其中
来表示Harary图,其中 表示Harary图的顶点数。若将其顶点表示成
表示Harary图的顶点数。若将其顶点表示成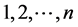 ,则两顶点用
,则两顶点用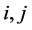 之间存在边当且仅当
之间存在边当且仅当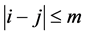 。图1给出当
。图1给出当 时的Harary图。
时的Harary图。
本文将Harary图 的顶点对距离进行分析,并给出修改的维纳指数,Harary指数和乘法维纳指数的计算公式。
的顶点对距离进行分析,并给出修改的维纳指数,Harary指数和乘法维纳指数的计算公式。
2. 主要结论及证明
根据Harary图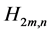 的定义,可知
的定义,可知 。图中取两个顶点
。图中取两个顶点 且满足
且满足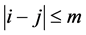 ,它们之间的距离为
,它们之间的距离为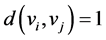 ,因此这个正则图边的数量为
,因此这个正则图边的数量为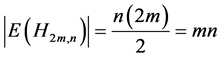 。另一方面从定义可知所有
。另一方面从定义可知所有 图的顶点都有相似的几何特征和拓扑结构,距离i点所有的路径总数就是顶点的个数。例如对
图的顶点都有相似的几何特征和拓扑结构,距离i点所有的路径总数就是顶点的个数。例如对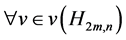 ,有2m条边,即有2m条距离为1的路径。从图的定义中可以看到
,有2m条边,即有2m条距离为1的路径。从图的定义中可以看到 和
和 ,
,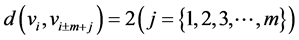 因为
因为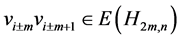 和
和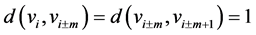 。显然
。显然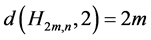 。因为
。因为
 ,
, 满足
满足 。因此
。因此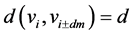
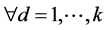 。显然
。显然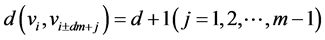 。由此可知,对于Harary图上的任意顶点
。由此可知,对于Harary图上的任意顶点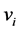 ,图的直径
,图的直径 就是
就是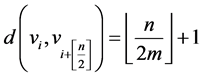 。同样顶点
。同样顶点 和
和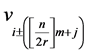 之间的距离也等于
之间的距离也等于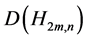 。对于所有的
。对于所有的 。容易看出如果
。容易看出如果 是奇数就由
是奇数就由 ,
, ,当n为偶数时
,当n为偶数时 。所以当n为奇数时对应的Hosoya多项式为:
。所以当n为奇数时对应的Hosoya多项式为:

当n为偶数时,设n = 2q,对应的Hosoya多项式为:

Figure 1. The Harary graph H6,10
图1. Harary图H6,10

综合以上分析和计算,当 为奇数时,
为奇数时,
 ,
,
 ,
,
 ,
,
 ,
,
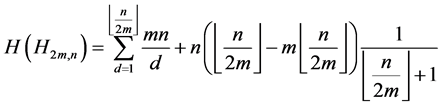 ,
,
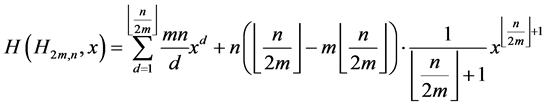 ,
,
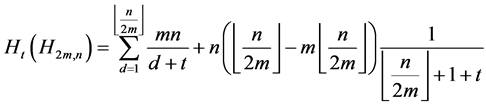 。
。
当 为偶数时,
为偶数时,


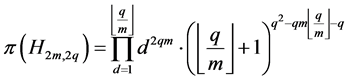 ,
,
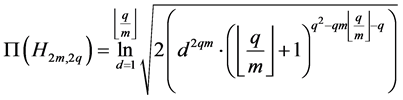 ,
,
 ,
,
 ,
,
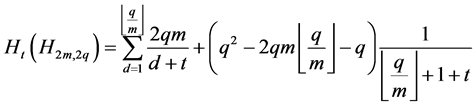 。
。
3. 总结
化学指数的计算是近10年来理论化学研究的重点内容。由于其结果可帮助科研工作者直接了解化合物的生物学和药理学特征,因此被广泛应用于化学、生物学、医学、药学、材料科学等领域。同时,其技术方法深受不发达国家和地区科研工作者的重视。
本文通过图结果分析,计算Harary图 中每一对顶点的距离,并由此对顶点对进行分类。再根据拓扑指数的定义得到若干与维纳指数相关的计算结果。
中每一对顶点的距离,并由此对顶点对进行分类。再根据拓扑指数的定义得到若干与维纳指数相关的计算结果。
文章引用
周兴丽,高 炜. Harary图H2m,n的基于距离的拓扑指数计算
Computation of Distance-Based Topological Indices for Harary Graph H2m,n[J]. 理论数学, 2016, 06(03): 151-156. http://dx.doi.org/10.12677/PM.2016.63022
参考文献 (References)
- 1. 冯前进, 刘润兰. 方剂图论和拓扑学[J]. 山西中医学院学报, 2013: 2-55.
- 2. 徐俊明. 图论及其应用[M]. 第2版. 合肥: 中国科学技术出版社, 2004: 3-4.
- 3. 骆崇亮. 随机二叉树的拓扑指数研究[D]. 北京: 中国科技大学, 2014.
- 4. Gao, W., Farahani, M.R. and Rajesh Kanna, M.R. (2015) Asian Academic Research Journal of Multidisciplinary. A Peer Reviewed International Journal of Asian Academic Research Associates, 2, 2319-2801.
- 5. 高云, 高炜. 修改的维纳指数和修改的超维纳指数的若干结果[J]. 生物物理学, 2015, 3(3): 59-66.
- 6. Farahani, M.R. (2013) Hosoya Poly-nomial Wiener and Hyper-Wiener Indices of Some Regular Graphs. Informatics Engineering an International Journal, 1, 10.
- 7. Diudea, M.V. (2002) Hosoya Polynomial in Tori. MATCH Communications in Mathematical and in Computer Chemistry, 45, 109-122.
- 8. Dobrynin, A.A., Entringer, R. and Gutman, I. (2001) Wiener Index of Trees: Theory and Ap-plications. Acta Applicandae Mathematicae, 66, 211-249. http://dx.doi.org/10.1023/A:1010767517079
- 9. Hosoya, H. (1989) On Some Counting Polynomials in Chemistry. Discrete Applied Mathematics, 19, 239-257. http://dx.doi.org/10.1016/0166-218X(88)90017-0
- 10. Klein, D.J., Lukovits, I. and Gutman, I. (1995) On the Definition of the Hyper-Wiener Index for Cycle-Containing Structures. Journal of Chemical Information and Computer Sciences, 35, 50-52. http://dx.doi.org/10.1021/ci00023a007
- 11. Knor, M., Potocnik, P. and Skrekovski, R. (2013) Wiener Index of Iterated Line Graphs of Trees Homeomorphic to the Claw K1;3. Ars Mathematica Contemporanea, 6, 211-219.
- 12. Randic, M. (1993) Novel Molecular Descriptor for Structure-Property Studies. Chemical Physics Letters, 211, 478. http://dx.doi.org/10.1016/0009-2614(93)87094-J
- 13. West, B. (2003) Introduction to Graph Theory. Prentice Hall of India.
- 14. Wiener, H. (1947) Structural Determination of Paraffin Boiling Points. Journal of the American Chemical Society, 69, 17-20. http://dx.doi.org/10.1021/ja01193a005
注释
文中的“ ”表示取其中最接近它的较小的一个整数。
”表示取其中最接近它的较小的一个整数。