Pure Mathematics
Vol.06 No.06(2016), Article ID:18993,6
pages
10.12677/PM.2016.66065
The Associative Form and Restrictiveness of Modular Lie Superalgebra 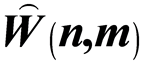
Qi Cui, Lihua Zhang
School of Mathematics and System Science, Shenyang Normal University, Shenyang Liaoning

Received: Nov. 2nd, 2016; accepted: Nov. 19th, 2016; published: Nov. 22nd, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, the nonsingular associative form of finite-dimensional simple modular Lie superalgebra 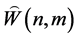 is given and proved, and the restrictiveness of
is given and proved, and the restrictiveness of 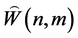 is discussed.
is discussed.
Keywords:Simple Modular Lie Superalgebra, Associative Form, Restricted Lie Superalgebra

模李超代数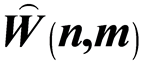 的结合型和限制性
的结合型和限制性
崔琪,张丽华
沈阳师范大学数学与系统科学学院,辽宁 沈阳

收稿日期:2016年11月2日;录用日期:2016年11月19日;发布日期:2016年11月22日

摘 要
本文给出并证明了有限维单模李超代数 具有非退化的结合型并且讨论了李超代数
具有非退化的结合型并且讨论了李超代数 的限制性。
的限制性。
关键词 :单模李超代数,结合型,限制李超代数

1. 引言
目前,有限维单模李超代数的分类问题还没有解决,所以文献 [1] 构造了新的有限维单模李超代数 ,并确定了它的单性,文献 [2] 确定了
,并确定了它的单性,文献 [2] 确定了 的导子超代数。
的导子超代数。
为了将 与已有的有限维单模李超代数进行比较,文本讨论了
与已有的有限维单模李超代数进行比较,文本讨论了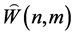 的结合型和限制性。
的结合型和限制性。
2. 回顾
回顾
下面将文献 [1] 构造的有限维单模李超代数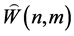 作简要回顾。用
作简要回顾。用 表示正整数集,
表示正整数集, 是特征数为
是特征数为 的域,设
的域,设 ,
, 为域
为域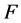 上具有
上具有 个未定元
个未定元 的外代数。
的外代数。
定义: ,
, 。
。
令 。
。
对 ,令
,令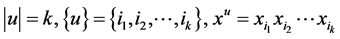 ,且约定
,且约定 ,则
,则 构成
构成 的一组
的一组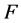 -基底。
-基底。
令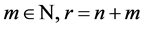 ,
,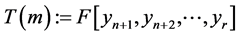 为满足
为满足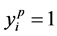 ,
, 的截头多项式代数。
的截头多项式代数。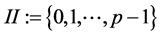 表示整数模
表示整数模 的剩余类环,
的剩余类环,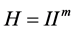 ,设
,设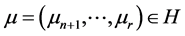 ,定义:
,定义: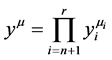 ,于是
,于是 ,
, 为
为 的
的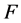 -基底。
-基底。
设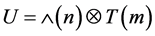 ,
,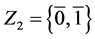 为模2的剩余类环,令:
为模2的剩余类环,令:

于是 是由
是由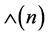 的
的 -阶化诱导出的结合超代数。
-阶化诱导出的结合超代数。
若 ,将
,将 简记为
简记为 ,于是
,于是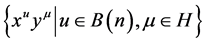 是
是 的一个
的一个 -基底。令
-基底。令 ,则
,则 是
是 -阶化的超代数,且
-阶化的超代数,且 。
。
令 。
。
对 ,令
,令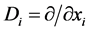 为
为 对
对 的偏导子,则
的偏导子,则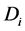 可以扩充为
可以扩充为 的导子,使得对
的导子,使得对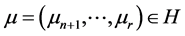 ,
,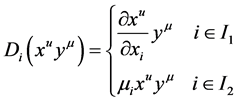 。
。
设 ,若
,若 ,则令
,则令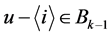 ,使得
,使得 ;
;
设 ,若
,若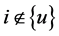 ,约定
,约定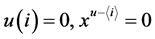 ,那么对任意的
,那么对任意的 ,有
,有 ,于是,若
,于是,若 ,则
,则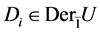 ,而若
,而若 ,则
,则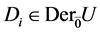 。
。
设 ,定义
,定义 ,那么:
,那么:

令 ,那么
,那么 为
为 的导子超代数
的导子超代数 的子代数,
的子代数, 为
为 一组
一组 -基底。下面简记
-基底。下面简记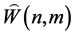 为
为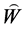 。
。
令 ,其中:
,其中:
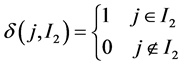 ,
,
那么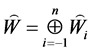 是
是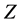 -阶化李超代数。
-阶化李超代数。
3. 结合型
引理3.1 [3] :设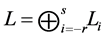 是有限维单
是有限维单 -阶化李超代数,置
-阶化李超代数,置 。假设
。假设 是一个超对称双线性型,并且满足下列条件:
是一个超对称双线性型,并且满足下列条件:
(a)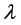 是
是 -不变的,即
-不变的,即 ;
;
(b)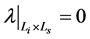 ,对
,对 ;
;
(c)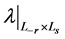 是
是 -不变的,即
-不变的,即 。
。
那么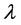 是
是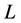 上的结合型。
上的结合型。
本文定义 ,使得
,使得 ,其中
,其中 ,
, ,显然
,显然 是线性的。
是线性的。
定理3.2 [4] : 具有非退化的结合型。
具有非退化的结合型。
证明:因为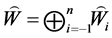 ,其中
,其中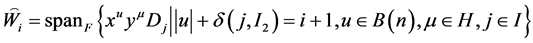 ,
,
所以: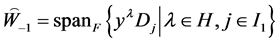 ,
,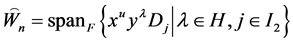

定义函数 ,显然
,显然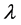 是双线性和超对称的。又因为
是双线性和超对称的。又因为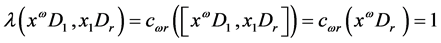 ,所以
,所以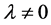 。下面验证
。下面验证 满足引理3.1中的三个条件:
满足引理3.1中的三个条件:
先验证(a),任取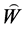 中的基向量
中的基向量 、
、 ,
, 中的基向量
中的基向量 ,其中
,其中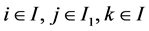 且
且 。
。
若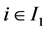 ,
,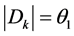 ,
, 或
或 ,有:
,有:

其中, ,
, ,且
,且 。
。
若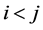 ,有:
,有:
若 ,有:
,有:
因此当 时
时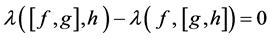
若 ,有
,有
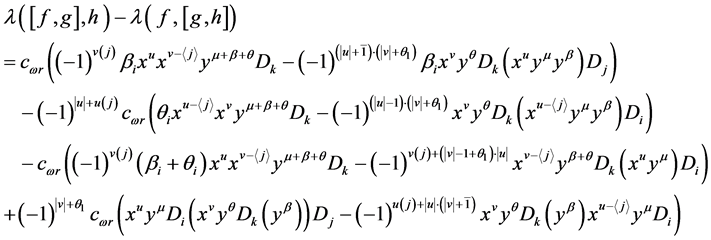
若 ,因为
,因为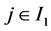 ,由
,由 定义,上式中除了第四项和第六项其余项均等于0。对于这两项,我们只需讨论
定义,上式中除了第四项和第六项其余项均等于0。对于这两项,我们只需讨论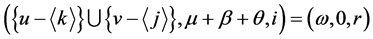 ,且
,且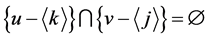 的情况,其余情况这两项均等于0。若
的情况,其余情况这两项均等于0。若 ,由于
,由于 ,所以第四项和第六项相加等于0;若
,所以第四项和第六项相加等于0;若 ,由于
,由于 ,所以第四项和第六项相加也等于0。
,所以第四项和第六项相加也等于0。
若 ,因为
,因为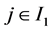 ,由
,由 定义,上式中第二项和第七项等于0。对于其余项,我们只需讨论如下几种情况:
定义,上式中第二项和第七项等于0。对于其余项,我们只需讨论如下几种情况:
①若 且
且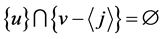 ,则上式等于
,则上式等于 由于
由于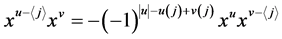 ,则该式等于0。
,则该式等于0。
②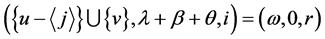 且
且 ,则上式等于
,则上式等于
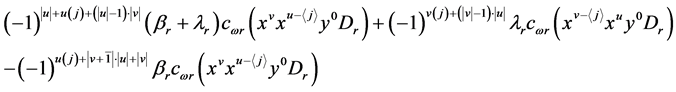
由于 ,则该式等于0。
,则该式等于0。
③若 ,由①②可知上式等于0成立。
,由①②可知上式等于0成立。
所以, 是
是 -不变的。
-不变的。
再验证(c),任取 中的基向量
中的基向量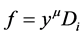 ,
, 中的基向量
中的基向量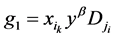 ,
, ,
, 中的基向量
中的基向量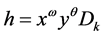 ,其中
,其中 且
且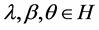 ,
, ,有
,有

若 ,则由
,则由 定义,上式等于0。
定义,上式等于0。
若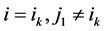 ,则上式等于
,则上式等于
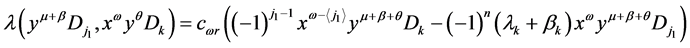 由
由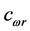 定义,该式等于0。
定义,该式等于0。
若 ,则上式等于
,则上式等于
 由
由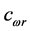 定义,该式等于0。
定义,该式等于0。
若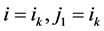 ,则上式等于
,则上式等于
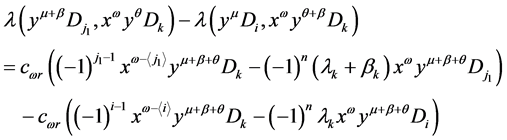
由 定义,该式等于0。
定义,该式等于0。
另一方面,

由 定义,该式等于0。
定义,该式等于0。
综上所述, 是
是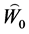 -不变的。
-不变的。
最后验证(b),任取 中的基向量
中的基向量 ,
,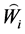 中的基向量
中的基向量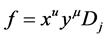 ,其中
,其中 ,有
,有 ,所以对任意的
,所以对任意的 ,
,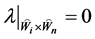 成立。
成立。
综上,由引理3.1可知,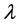 是
是 上一个结合型显然,
上一个结合型显然, 。由
。由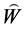 的单性,知
的单性,知 是非退化的。
是非退化的。
4. 限制性
引理4.1 [5] :设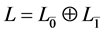 是域
是域 上的李超代数,
上的李超代数,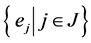 是
是 的一组
的一组 -齐次基底。如果存在
-齐次基底。如果存在 ,使得对任意的
,使得对任意的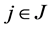 ,有
,有 ,其中
,其中 ,若
,若 ;
; ,若
,若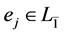 ,则
,则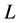 是一个限制李超代数。
是一个限制李超代数。
定理4.2:有限维模李超代数 是限制李超代数。
是限制李超代数。
证明:设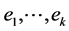 与
与 分别为
分别为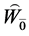 和
和 的一组基,下面证明
的一组基,下面证明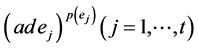 为内导子。下面分两种情况讨论:
为内导子。下面分两种情况讨论:
(1) ,则
,则 。
。
对任意的 ,因
,因 是偶导子,由Leibniz公式,有:
是偶导子,由Leibniz公式,有:
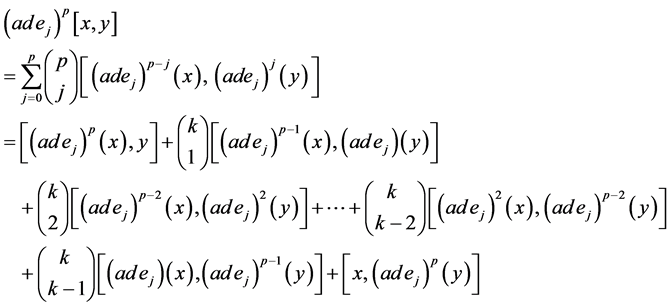
又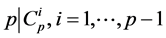 ,而
,而 是特征为
是特征为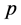 的域上的李超代数,所以有:
的域上的李超代数,所以有:

所以, 。
。
(2) ,则
,则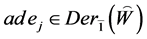 。
。
对任意的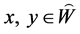 ,因为:
,因为:

所以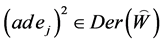 。
。
由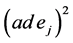 是偶导子及
是偶导子及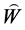 是特征为
是特征为 的域上的李超代数,仿照(1),有
的域上的李超代数,仿照(1),有

所以,
由于 ,所以
,所以 都为内导子,因此有限维模李超代数
都为内导子,因此有限维模李超代数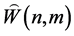 是限制李超代数。
是限制李超代数。
文章引用
崔 琪,张丽华. 模李超代数W⌒(n,m)的结合型和限制性
The Associative Form and Restrictiveness of Modular Lie Superalgebra W⌒(n,m)[J]. 理论数学, 2016, 06(06): 474-479. http://dx.doi.org/10.12677/PM.2016.66065
参考文献 (References)