Pure Mathematics
Vol.
11
No.
08
(
2021
), Article ID:
44497
,
6
pages
10.12677/PM.2021.118166
n-强-F-Ding投射模
钟魁晨
西北师范大学数学与统计学院,甘肃 兰州
收稿日期:2021年6月30日;录用日期:2021年8月4日;发布日期:2021年8月11日

摘要
引入n-强-F-Ding投射模,给出n-强-F-Ding投射模的等价刻画和基本性质,证明了一个模M是n-强-F-Ding投射模当且仅当M同构于某个n-强-F-Ding投射模与投射模的直和。
关键词
Ding投射模,n-强Ding投射模,n-强-F-Ding投射模

n-Strongly-F-Ding Projective Modules
Kuichen Zhong
College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu
Received: Jun. 30th, 2021; accepted: Aug. 4th, 2021; published: Aug. 11th, 2021

ABSTRACT
In this paper, we introduce n-Strongly-F-Ding projective module, give its equivalent characterization and basic properties, and prove that a module is n-Strongly-F-Ding projective module if and only if it is isomorphic to a direct sum of a n-Strongly-F-Ding projective module and a projective module.
Keywords:Ding Projective Module, n-Strongly-F-Ding Projective Module, n-Strongly-F-Ding Projective Module

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1995年,在文献 [1] 中,Enochs等人在任意结合环上引入了Gorenstein投射(内射,平坦)模的定义,推广了G-维数为0的有限生成模。2007年,Bennis和Mahdou在文献 [2] 中,引入了特殊的Gorenstein模,即强Gorenstein投射(内射,平坦)模的概念,给出强Gorenstein投射模的等价刻画,并且证明了一个模M是Gorenstein投射模当且仅当它是某个强Gorenstein投射模的直和项。在文献 [3] 中,Zhao和Huang引入n-强Gorenstein投射(内射,平坦)模的概念,研究这类模的性质。
2009年,在文献 [4] 中,Mao和Li等定义了强Gorenstein平坦模,即Ding投射模。证明了在凝聚环下,Ding投射模是Gorenstein平坦模。同年在文献 [5] 中,Xing定义了n-强Ding投射模的概念,证明了在交换环的情况下,一个模M是n-强Ding投射模,那么模M与投射模的张量是n-强Ding投射模。
2011年,在文献 [6] 中,作者引入了X-Gorenstein投射和Y-Gorenstein内射(平坦)模及它们的维数,研究了这类模的性质,给出了X-Gorenstein投射和Y-Gorenstein内射(平坦)维数的等价条件。
受以上启发,本文引入n-强-F-Ding投射模,研究它的性质,并给出它的等价条件。
本文中的环R均指有单位元的结合环,模指左R-模。Proj,Flat分别表示投射模类,平坦模类。
2. 预备知识
定义1.1 [1] 称R-模M是Gorenstein投射模,如果存在投射模的正合序列
,
其中 ,使得 ,且对 , 保持以上序列正合。记M为GP模。所有GP模的类记为 。
定义1.2 [4] 称R-模M是Ding投射模,如果存在投射模的正合序列
,
其中 ,使得 ,且对 , 保持以上序列正合。记M为Ding投射模。所有Ding投射模的类记为 。
定义1.3 [6] 设n是正整数。称R-模M是n-强Ding投射模,如果存在R-模的正合序列
,
其中 ,且对 , 保持以上序列正合。记M为 模。所有 模的类记为 。
注: 。
3. 主要结果
定义2.1 设n是正整数,F是包含所有平坦模的类,称R-模M是n-强-F-Ding投射模,如果存在R-模的正合序列
,
其中 ,且对 , 保持以上序列正合。记M为 模。所有 模的类记为 。
注1: 。
命题2.2 设 是一簇 模,那么 是 模。
证 通过定义对 有正合列
,
其中 ,对 , 作用下依旧正合。所以有正合列
,
其中 ,对 , 作用下依旧正合。通过定义知 是 模。
引理2.3 如果存在正合列
,
其中 且 ,那么 。
对照文献 [7] 的定义我们可以定义R-模M的F-投射维数 。当n不存在时记 ,下面给出n-强F-Ding投射模的等价刻画:
命题2.4 n是正整数,设M是R-模,则以下等价:
1) 。
2) 存在R-模的短正合列
,
其中 ,且对 ,。
3) 存在R-模的短正合列
,
其中 ,且对 ,。
证 , 显然。现在证 。
假设 。则有正合列
,
其中 。取 ,,其中 则有短正合列
,
,
,
,
对短正合列 用 作用并由长正合列定理及维数转移可得
,
故 。
我们回顾一下投射可解的定义,称R-模类X是投射可解的,那么对于R-模的短正合列 ,若 ,则 当且仅当 。而我们知道n-强Gorenstein模类通常情况下并不投射可解。那么我们思考当在什么情况下有相似于投射可解的结论呢?于是我们有如下结果:
命题2.5 设 ,是R-模的短正合列,其中P是投射模,则 当且仅当 。
证 因为 ,则通过定义存在R-模的正合列
,
其中 ,且对 , 作用下依旧正合。那么有R-模的正合列
,
通过定义知 。
由于 ,且 ,则通过定义知存在R-模的正合列
,
取 ,,由引理2.4 。
由推出图
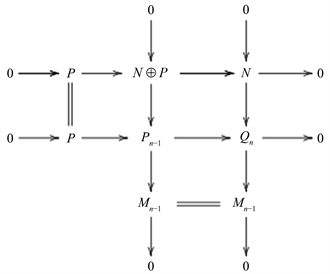
考虑短正合列
,
用 作用并由长正合列定理以及维数转移可得
因为 ,则
所以 。即中间行的正合列可裂,可得 ,且有短正合列
对 , 作用下依旧正合。
由拉回图
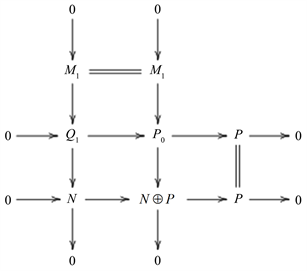
考虑到短正合列 可裂,可得 。且有短正合列
,
对 , 作用下依旧正合。从而有正合列
,
对 , 作用下依旧正合。
命题2.6 设 , 是R-模的短正合列。若 ,则 。
证 由于 ,则存在R-模的正合列
,
其中 ,取 ,由引理2.3知 。
考虑拉回图
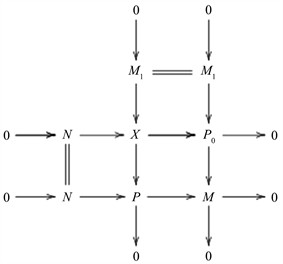
因为短正合列 可裂,所以 ,由命题2.4知 。
推论2.7 设 ,是R-模的短正合列,其中 ,则 当且仅当 。
命题2.8 设R是交换环, 。若 ,则 。
证 因为 ,则存在R-模的正合列
,
其中 ,那么
,
因为R是交换环,所以 ,由于
,
通过命题2.3知 。
文章引用
钟魁晨. n-强-F-Ding投射模
n-Strongly-F-Ding Projective Modules[J]. 理论数学, 2021, 11(08): 1482-1487. https://doi.org/10.12677/PM.2021.118166
参考文献
- 1. Enochs, E.E. and Jenda, O.M.G. (1995) Gorenstein Injective and Projective Modules. Mathmatische Zeitschrift, 220, 611-633. https://doi.org/10.1007/BF02572634
- 2. Bennis, D. and Mahdou, N. (2007) Strongly Gorenstein Pro-jective, Injective and Flat Modules. Journal of Pure and Applied Algebra, 210, 437-445. https://doi.org/10.1016/j.jpaa.2006.10.010
- 3. Zhao, G.Q. and Huang, Z.Y. (2011) n-Strongly Gorenstien Pro-jective, injective and Flat Modules. Communications in Algebra, 39, 3044-3062. https://doi.org/10.1080/00927872.2010.496749
- 4. Ding, N.G., Li, Y.L. and Mao, L.X. (2009) Strongly Gorenstein Flat Modules. Journal of the Australian Mathematical Society, 86, 323-338. https://doi.org/10.1017/S1446788708000761
- 5. Xing, J. (2012) n-Strongly Ding Projective, Injective and Flat Modules. International Mathematical Forum, 41-44, 2093-2098.
- 6. Meng, F.Y. and Pan, Q.X. (2011) X-Gorenstein Projective and Y-Gorenstein Injective Modules. Hacettepe Journal of Mathematics and Statistics, 40, 537-554.
- 7. Hu, Y., Zhou, J. and Zhao, Z.B. (2020) X-Strongly Gorenstein Modules. Journal of University of Science and Technology of China, 50, 128-131.