西北师范大学数学与统计学院，甘肃 兰州

收稿日期：2023年1月5日；录用日期：2023年2月6日；发布日期：2023年2月14日

摘要

设R和S均是环，本文研究了Gorenstein(n, d)-投射模及其一些基本性质，进一步，设 $f:R\to S$ 是一个环的满同态，给出了Gorenstein(n, d)-投射模的一个等价刻画。

关键词

Gorenstein(n, d)-投射模，n-凝聚环

Gorenstein(n, d)-Projective Modules

Lili Liu

College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu

Received: Jan. 5^th, 2023; accepted: Feb. 6^th, 2023; published: Feb. 14^th, 2023

ABSTRACT

Let R and S be rings, In this paper, Gorenstein(n, d)-projective modules and some of their basic properties are studied. Moreover, let $f:R\to S$ be asurjectivering homomorphism, an equivalent characterization of Gorenstein(n, d)-projective modules is given.

Keywords:Gorenstein(n, d)-Projective Module, n-Coherent Ring

Copyright © 2023 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

投射模是同调代数理论研究中非常重要的一种古典模类，上世纪九十年代，Enochs等 [1] 在任意结合环上引入Gorenstein投射模的概念，这是Auslander等引入的G-维数为0模的推广，也是经典同调代数中投射模在相对同调代数中的对应。此后，Gorenstein投射模受到了国内外学者的广泛关注。文献 [2] 中给出了(n, d)-投射模的定义，在此基础上我们对(n, d)-投射模进行了推广，给出了Gorenstein(n, d)-投射模的定义，并且对Gorenstein(n, d)-投射模进行了一般研究。

2. 预备知识

文中R和S均是有单位元的结合环，模均指酉模。我们用R-模(S-模)表示左R-模(左S-模)，R^OP-模(S^OP-模)表示右R-模(右S-模)。设n，d都是非负整数。 $i{d}_R\left(N\right)$ 表示R^OP-模N的内射维数。

定义1.1 R^OP-模U称为n-表现模 [3] ，如果存在R^OP-模的正合列

$F_n\to F_{n-1}\to \cdots \to F_1\to F_0\to U\to 0$ ,

其中每个 $F_i$ 都是有限生成自由模 $\left(i=0,1,2,\cdots ,m\right)$ 。

R是右n-凝聚环 [3] ，如果对任意n-表现R^OP-模是(n + 1)-表现的。

R^OP-模N称为(n, d)-内射模 [3] ，如果对任意n-表现R^OP-模U， ${\text{Ext}}_R^{d+1}\left(U,N\right)=0$ 。

R^OP-模M称为(n, d)-投射模 [2] ，如果对任意(n, d)-内射R^OP-模N， ${\text{Ext}}_R^1\left(M,N\right)=0$ 。

注1.2 [4] 设R是环，m和n是整数，则以下成立：

1) 当 $m\ge n$ 时，任意m-表现R^OP-模是n-表现的。

2) 当 $m\ge n$ 时，任意(n, d)-内射R^OP-模是(m, d)-内射的。

3) 当 $m\ge n$ 时，任意(m, d)-投射R^OP-模是(n, d)-投射的。

3. Gorenstein(n, d)-投射模

定义2.1 称R^OP-模G是Gorenstein(n, d)-投射模，如果存在(n, d)-投射R^OP-模的正合列

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

使得 $G\cong \text{Ker}\left(P^0\to P^1\right)$ ，并且对任意内射维数有限的(n, d)-内射R^OP-模N， ${\text{Hom}}_R\left(P,N\right)$ 正合。

定理2.2 设R是环，G是R^OP-模。若R是一个右n-凝聚环，则G是Gorenstein(n, d)-投射模当且仅当存在(n, d)-投射R^OP-模的正合列

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

使得 $G\cong \text{Ker}\left(P^0\to P^1\right)$ 。

证明 必要性由定义显然成立。

设(n, d)-内射R^OP-模N，且 $i{d}_R\left(N\right)=m<\infty$ ，下证G是Gorenstein(n, d)-投射模。

考虑短正合列 $0\to N\to E\to K\to 0$ ，其中E是内射模。对m进行归纳，当 $m=0$ ，显然 ${\text{Hom}}_R\left(P,N\right)$ 正合。 $i{d}_R\left(N\right)=m$ 时，因为内射模是(n, d)-内射的，由文献 [2] 中引理3.4知(n, d)-内射模关于单同态的余核封闭，所以K是(n, d)-内射R^OP-模。并且对任意 $i\ge 0$ ， $P_i$ 和 $P^i$ 都是(n, d)-投射R^OP-模。故 ${\text{Ext}}_R^1\left(P_i,K\right)={\text{Ext}}_R^1\left(P^i,K\right)=0$ 。得下面正合复形

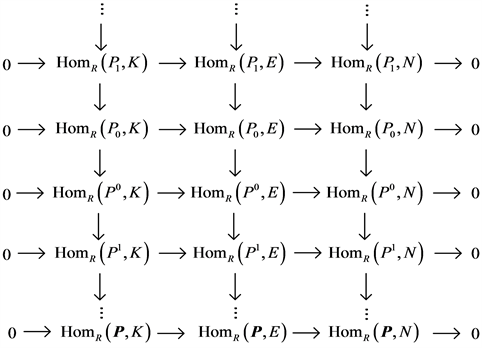
$i{d}_R\left(K\right)=m-1$ ，由归纳假定知 ${\text{Hom}}_R\left(P,K\right)$ 正合。再由复形的长正合列定理，即 ${\text{Hom}}_R\left(P,N\right)$ 正合，得证。

推论2.3 设R是一个右n-凝聚环，G是R^OP-模。则以下等价：

(1) G是Gorenstein(n, d)-投射模。

(2) 存在(n, d)-投射R^OP-模正合列 $0\to G\to P^0\to P^1\to \cdots$ 。

(3) 存在R^OP-模短正合列 $0\to G\to M\to L\to 0$ ，其中M是(n, d)-投射模，L是Gorenstein(n, d)-投射模。

证明 (1) $\Rightarrow$ (2)，(1) $\Rightarrow$ (3)显然。

(2) $\Rightarrow$ (1)对任意R^OP-模G，存在正合序列 $\cdots \to P_1\to P_0\to G\to 0$ ，其中 $P_i\left(i\ge 0\right)$ 是投射模。因为投射模是(n, d)-投射的，连接这两个序列得到(n,d)-投射R^OP-模正合序列 $\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ，使得 $G\cong \text{Ker}\left(P^0\to P^1\right)$ 。由定理2.2可得G是Gorenstein(n, d)-投射模。

(3) $\Rightarrow$ (2) 设R^OP-模短正合列 $0\to G\to M\to L\to 0$ ，其中M是(n, d)-投射模，L是Gorenstein(n, d)-投射模，由(1) $\Rightarrow$ (2)，存在正合序列 $0\to L\to P^{0^{\prime }}\to P^{1^{\prime }}\to P^{2^{\prime }}\to \cdots$ ，其中 $P^{i^{\prime }}\left(i\ge 0\right)$ 是(n, d)-投射模，连接两序列得到正合序列 $0\to G\to M\to P^{0^{\prime }}\to P^{1^{\prime }}\to P^{2^{\prime }}\to \cdots$ ，即为所求。

命题2.4 设R是一个右n-凝聚环，G是R^OP-模。若R是(n, d)环且G是Gorenstein(n, d)-投射模，则对任意整数 $i\ge 1$ 和任意内射维数有限的(n, d)-内射R^OP-模N， ${\text{Ext}}_{}^i\left(G,N\right)=0$ 。

证明设G是Gorenstein(n, d)-投射R^OP-模，则存在G的(n, d)-投射分解

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

将此序列打断

对任意(n, d)-内射R^OP-模N，且 ${\text{id}}_R\left(N\right)<\infty$ ，以函子 $\text{Hom}\left(-,N\right)$ 作用短正合列仍正合，并且G， $K_i\left(i\ge 0\right)$ 都是Gorenstein(n, d)-投射R^OP-模，所以 ${\text{Ext}}_{}^1\left(\text{G},N\right)={\text{Ext}}_{}^1\left(K_i,N\right)=0$ 。在短正合列 $0\to K_0\to P_0\to \text{G}\to 0$ 中，由长正合序列引理得 $\cdots \to {\text{Ext}}_{}^1\left(K_0,N\right)\to {\text{Ext}}_{}^2\left(\text{G},N\right)\to {\text{Ext}}_{}^2\left(P_0,N\right)\to \cdots$ ，又R是(n, d)环，由文献 [2] 中定理4.4知(n, d)投射模是投射的，得 ${\text{Ext}}_{}^2\left(G,N\right)=0$ 。在短正合列 $0\to K_1\to P_1\to K_0\to 0$ 中，由长正合序列引理得 $\cdots \to {\text{Ext}}_{}^1\left(K_1,N\right)\to {\text{Ext}}_{}^2\left(K_0,N\right)\to {\text{Ext}}_{}^2\left(P_1,N\right)\to \cdots$ ，得 ${\text{Ext}}_{}^2\left(K_0,N\right)=0$ 。由序列 $\cdots \to {\text{Ext}}_{}^2\left(K_0,N\right)\to {\text{Ext}}_{}^3\left(\text{G},N\right)\to {\text{Ext}}_{}^3\left(P_0,N\right)\to \cdots$ ，得 ${\text{Ext}}_{}^3\left(\text{G},N\right)=0$ 。依此类推，对任意整数 $i\ge 1$ ，故 ${\text{Ext}}_{}^i\left(G,N\right)=0$ 。

我们用 ${\text{G}}_n^d{\text{-pd}}_R\left(G\right)$ 表示R^OP-模G的Gorenstein(n, d)-投射维数， ${\text{G}}_n^d{\text{-pd}}_R\left(G\right)\le m$ 当且仅当G有长度为m的Gorenstein(n, d)-投射分解。

命题2.5 设R是一个右n-凝聚环，存在R^OP-模短正合列 $0\to K\to B\to G\to 0$ ，若B是(n, d)投射模，则 ${\text{G}}_n^d{\text{-pd}}_R\left(G\right)\le {\text{G}}_n^d{\text{-pd}}_R\left(K\right)+1$ 。特别地，若G是Gorenstein(n, d)-投射R^OP-模，则K也是。

证明 设 ${\text{G}}_n^d{\text{-pd}}_R\left(K\right)=m<\infty$ ，则K存在长度为m的Gorenstein(n, d)-投射分解 $0\to B_m\to B_{m-1}\to \cdots \to B_0\to K\to 0$ 。连接此序列和短正合列 $0\to K\to B\to G\to 0$ ，得G的Gorenstein(n, d)-投射分解 $0\to B_m\to B_{m-1}\to \cdots \to B_0\to B\to G\to 0$ ，故 ${\text{G}}_n^d{\text{-pd}}_R\left(G\right)\le m+1={\text{G}}_n^d{\text{-pd}}_R\left(K\right)+1$ 。

特殊情况由推论1可得。

命题2.6 设R是一个右n-凝聚环， $0\to A\to G\to H\to 0$ 是R^OP-模短正合列。若A是Gorenstein(n, d)-投射模，H是(n, d)投射模，则G是Gorenstein(n, d)-投射的。

证明 若A是Gorenstein(n, d)-投射R^OP-模，则存在R^OP-模正合列 $0\to A\to M\to L\to 0$ ，其中，M是(n, d)投射模，L是Gorenstein(n, d)-投射的。

考虑下面的推出图

在行正合列 $0\to M\to D\to H\to 0$ 中，因为(n, d)投射模关于扩张封闭，所以D是(n, d)投射模。在列正合列 $0\to G\to D\to L\to 0$ 中，D是(n, d)投射模，L是Gorenstein(n, d)-投射模，由推论2.3，G是Gorenstein(n, d)-投射的。

命题2.7 设R是环，m和n是整数。则以下成立：

1) 当 $m\ge n$ 时，任意Gorenstein(m, d)-投射R^OP-模是Gorenstein(n, d)-投射的。

2) 若R是一个右n-凝聚环，当 $m\ge n$ 时，任意Gorenstein(n, d)-投射R^OP-模是Gorenstein(m, d)-投射的。

证明 1) 设G是Gorenstein(m, d)-投射R^OP-模。当 $m\ge n$ 时，任意(m, d)-投射R^OP-模是(n, d)-投射的。则存在(n, d)-投射R^OP-模正合列

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

又因为任意(n, d)-内射R^OP-模是(m, d)-内射的，对任意内射维数有限的(n, d)-投射R^OP-模N， $\text{Hom}\left(P,N\right)$ 正合，故G是Gorenstein(n, d)-投射的。

2) 设G是Gorenstein(n, d)-投射R^OP-模，R是一个右n-凝聚环。当 $m\ge n$ 时，n表现R^OP-模是m表现的，故(m, d)-内射R^OP-模是(n, d)-内射的且(n, d)-投射R^OP-模是(m, d)-投射的。则存在(m, d)-投射R^OP-模正合列

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

对任意内射维数有限的(m, d)-投射R^OP-模N， $\text{Hom}\left(P,N\right)$ 正合，故G是Gorenstein(m, d)-投射的。

引理2.8 设 $f:R\to S$ 是一个环的满同态， $S_R^{}$ 是投射R^OP-模且 ${}_R{}^{}S$ 是投射R-模。若M是(n, d)-投射S^OP-模，则 $M{\otimes }_{S}S$ 是一个(n, d)-投射R^OP-模。

证明 设N是(n, d)-内射R^OP-模，由文献 [4] 中引理4.1可得 ${\text{Hom}}_R\left(S,N\right)$ 是一个(n, d)-内射S^OP-模。M是(n, d)-投射S^OP-模，由文献 [5] 中推论10.65，则有同构

${\text{Ext}}_R^1\left(M{\otimes }_{S}S,N\right)\cong {\text{Ext}}_S^1\left(M,{\text{Hom}}_R\left(S,N\right)\right)=0,$

得 ${\text{Ext}}_R^1\left(M{\otimes }_{S}S,N\right)=0$ ，故 $M{\otimes }_{S}S$ 是一个(n, d)-投射R^OP-模。

引理2.9 设 $f:R\to S$ 是一个环的满同态， $S_R^{}$ 是投射R^OP-模且 ${}_R{}^{}S$ 是投射R-模。若M是(n, d)-投射R^OP-模，则 $M{\otimes }_{R}S$ 是一个(n, d)-投射S^OP-模。

证明 设N是(n, d)-内射S^OP-模，则N是(n, d)-内射R^OP-模。由文献 [5] 中推论10.65，则有同构

${\text{Ext}}_S^1\left(M{\otimes }_{R}S,N\right)\cong {\text{Ext}}_R^1\left(M,{\text{Hom}}_S\left(S,N\right)\right)\cong {\text{Ext}}_R^1\left(M,N\right)=0$ ,

得 ${\text{Ext}}_S^1\left(M{\otimes }_{R}S,N\right)=0$ ，故 $M{\otimes }_{R}S$ 是一个(n, d)-投射S^OP-模。

命题2.10 设 $f:R\to S$ 是一个环的满同态， $S_R^{}$ 是投射R^OP-模且 ${}_R{}^{}S$ 是投射R-模。若N是一个R^OP-模且 ${\text{id}}_R\left(N\right)<\infty$ ，则 ${\text{id}}_S\left({\text{Hom}}_R\left(S,N\right)\right)<\infty$ 。

证明 设任意S^OP-模M，由文献 [5] 中推论10.65得同构式

${\text{Ext}}_S^n\left(M,{\text{Hom}}_R\left(S,N\right)\right)\cong {\text{Ext}}_R^n\left(M{\otimes }_{S}S,N\right)$ .

若 ${\text{id}}_R\left(N\right)=0$ ，N是一个内射R^OP-模， $n\ge 1$ 时，上式右边等于零，故 ${\text{Ext}}_S^{n\ge 1}\left(M,{\text{Hom}}_R\left(S,N\right)\right)=0$ ，得 ${\text{Hom}}_R\left(S,N\right)$ 是一个内射S^OP-模，即 ${\text{id}}_S\left({\text{Hom}}_R\left(S,N\right)\right)=0$ 。

若 ${\text{id}}_R\left(N\right)=m<\infty$ ，由上面同构式 ${\text{Ext}}_S^{m+1}\left(M,{\text{Hom}}_R\left(S,N\right)\right)\cong {\text{Ext}}_R^{m+1}\left(M{\otimes }_{S}S,N\right)=0$ ，得 ${\text{id}}_S\left({\text{Hom}}_R\left(S,N\right)\right)=m$ 。

综上， ${\text{id}}_S\left({\text{Hom}}_R\left(S,N\right)\right)<\infty$ 。

定理2.11设 $f:R\to S$ 是一个环的满同态， $S_R^{}$ 是投射R^OP-模且 ${}_R{}^{}S$ 是投射R-模，M是一个S^OP-模。则以下价：

(1) $M_R^{}$ 是Gorenstein(n, d)-投射R^OP-模。

(2) $M{\otimes }_{R}S$ 是Gorenstein(n, d)-投射S^OP-模。

(3) $M_S^{}$ 是Gorenstein(n, d)-投射S^OP-模。

证明 (1) $\Rightarrow$ (2)设N是(n, d)-内射S^OP-模且 ${\text{id}}_S\left(N\right)<\infty$ ，由文献 [6] 中引理3.12知N是(n, d)-内射R^OP-模且 ${\text{id}}_R\left(N\right)<\infty$ 。再由文献 [4] 中引理4.1得 ${\text{Hom}}_R\left(S,N\right)$ 是(n, d)-内射S^OP-模，故 ${\text{Hom}}_R\left(S,N\right)$ 也是(n, d)-内射R^OP-模。由命题2.10得 ${\text{id}}_S\left({\text{Hom}}_R\left(S,N\right)\right)<\infty$ ，同时 ${\text{id}}_R\left({\text{Hom}}_R\left(S,N\right)\right)<\infty$ 。由(1) $M_R^{}$ 是Gorenstein(n, d)-投射R^OP-模，存在(n, d)-投射R^OP-模的正合列

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

其中， $M_R^{}\cong \text{Ker}\left(P^0\to P^1\right)$ 。即存在(n, d)-投射S^OP-模的正合列

$P{\otimes }_{R}S=\cdots \to P_1{\otimes }_{R}S\to P_0{\otimes }_{R}S\to P^0{\otimes }_{R}S\to P^1{\otimes }_{R}S\to \cdots$ ,

其中， $M{\otimes }_{R}S\cong \text{Ker}\left(P^0{\otimes }_{R}S\to P^1{\otimes }_{R}S\right)$ 。由伴随同构

${\text{Hom}}_R\left(P,{\text{Hom}}_S\left(S,N\right)\right)\cong {\text{Hom}}_S\left(P{\otimes }_{R}S,N\right)$ .

对任意内射维数有限的(n, d)-内射R^OP-模 ${\text{Hom}}_R\left(S,N\right)$ ，因为f满，由文献 [5] 命题8.33，所以 ${\text{Hom}}_R\left(S,N\right)={\text{Hom}}_S\left(S,N\right)$ 。由条件(1)， ${\text{Hom}}_R\left(P,{\text{Hom}}_S\left(S,N\right)\right)$ 正合，故对任意(n, d)-内射S^OP-模N且 ${\text{id}}_S\left(N\right)<\infty$ ， ${\text{Hom}}_S\left(P{\otimes }_{R}S,N\right)$ 正合，得 $M{\otimes }_{R}S$ 是Gorenstein(n, d)-投射S^OP-模。

(2) $\Rightarrow$ (3)由 $M{\otimes }_{R}S=M_S^{}$ ，故 $M_S^{}$ 是Gorenstein(n, d)-投射S^OP-模。

(3) $\Rightarrow$ (1)设P是(n, d)-投射S^OP-模，则P是(n, d)-投射R^OP-模。 $M_S^{}$ 是Gorenstein(n, d)-投射S^OP-模，则存在(n, d)-投射R^OP-模的正合列

$P=\cdots \to P_1\to P_0\to P^0\to P^1\to \cdots$ ,

其中， $M_R^{}\cong \text{Ker}\left(P^0\to P^1\right)$ 。设N是(n, d)-内射R^OP-模且 ${\text{id}}_R\left(N\right)<\infty$ 。由文献 [4] 引理4.1和命题2.10得 ${\text{Hom}}_R\left(S,N\right)$ 是一个(n, d)-内射S^OP-模且 ${\text{id}}_S\left({\text{Hom}}_R\left(S,N\right)\right)<\infty$ 。由同构

${\text{Hom}}_S\left(P,{\text{Hom}}_R\left(S,N\right)\right)\cong {\text{Hom}}_R\left(P{\otimes }_{S}S,N\right)\cong {\text{Hom}}_R\left(P,N\right)$ ,

由条件(3)，对任意内射维数有限的(n, d)-内射S^OP-模 ${\text{Hom}}_R\left(S,N\right)$ ， ${\text{Hom}}_S\left(P,{\text{Hom}}_R\left(S,N\right)\right)$ 正合，故对任意(n, d)-内射R^OP-模N且 ${\text{id}}_R\left(N\right)<\infty$ ， ${\text{Hom}}_R\left(P,N\right)$ 正合，得 $M_R^{}$ 是Gorenstein(n, d)-投射R^OP-模。

文章引用

刘立丽. Gorenstein(n, d)-投射模
Gorenstein(n, d)-Projective Modules[J]. 理论数学, 2023, 13(02): 166-171. https://doi.org/10.12677/PM.2023.132019

参考文献