Operations Research and Fuzziology
Vol.06 No.02(2016), Article ID:17652,6
pages
10.12677/ORF.2016.62008
Combined Homotopy Method for Inequality Constrained Problems
Qingqun Huang
School of Mathematics and Statistics, Hechi University, Yizhou Guangxi

Received: May 4th, 2016; accepted: May 23rd, 2016; published: May 26th, 2016
Copyright © 2016 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
For the optimization problem with inequality constraints, this paper constructs a new homotopy equation which with the Newton’s method to get a combined homotopy Newton algorithm. The global linear convergence of the algorithm is proved at the end.
Keywords:Combined Homotopy, Convex Nonlinear Programming, Global Convergence, Newton Method

组合同伦法求不等式约束问题
黄青群
河池学院数学与统计学院,广西 宜州

收稿日期:2016年5月4日;录用日期:2016年5月23日;发布日期:2016年5月26日

摘 要
对含不等式约束的优化问题,构造一个新的同伦方程,与牛顿法相结合得到一个组合同伦牛顿算法,最后给出了该算法的全局线性收敛性的证明。
关键词 :组合同伦,凸非线性规划,全局收敛性,牛顿法

1. 引言
1976年,Smale [1] 及Kellogg [2] 提出了著名的同伦法后,近几十年来,组合同伦法就成为了不动点问题、非线性问题、均衡约束问题、非线性互补问题及多目标优化问题等诸多非线性问题的最优求解方法 [3] - [7] 。
同伦方法的基本思想是:为求解非线性方程组
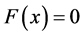 ,
,
其中 是光滑映射,构造带参数
是光滑映射,构造带参数 的同伦映射
的同伦映射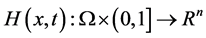 ,使之满足
,使之满足
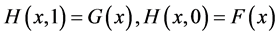 ,
,
其中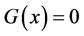 的解
的解 为已知。只要
为已知。只要 构造得合适,在特定的条件下,同伦方程就可确定一条从
构造得合适,在特定的条件下,同伦方程就可确定一条从 出发,趋于超平面
出发,趋于超平面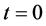 的光滑曲线,称之为同伦路径,而该曲线另一端的任意极限点的
的光滑曲线,称之为同伦路径,而该曲线另一端的任意极限点的 分量
分量 就是
就是 在
在 中的解。因此可通过数值跟踪该曲线从而得到
中的解。因此可通过数值跟踪该曲线从而得到 的解。本文对含不等式约束的优化问题提出了一个同伦路径跟踪方法,即通过构造一个新的同伦方程,与牛顿法相结合的得到一个组合同伦牛顿算法,最后给出了该算法的全局线性收敛性的证明。
的解。本文对含不等式约束的优化问题提出了一个同伦路径跟踪方法,即通过构造一个新的同伦方程,与牛顿法相结合的得到一个组合同伦牛顿算法,最后给出了该算法的全局线性收敛性的证明。
考虑下列不等式约束规划问题:
 (1)
(1)
其中 ,
, ,
, ,
, 为充分光滑函数,且
为充分光滑函数,且 为严格凸函数,
为严格凸函数,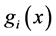 ,
, 为凸函数。定义问题(1)的可行域集合为
为凸函数。定义问题(1)的可行域集合为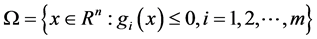 ,严格可行域集合为
,严格可行域集合为 。如果
。如果 ,则问题(1)的解存在的充要条件是存在
,则问题(1)的解存在的充要条件是存在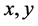 为下列K-K-T方程的解:
为下列K-K-T方程的解:
 (2)
(2)
其中
 ,
, ,
, ,
,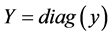 ,
, ,
, 为是(1)的约束拉格朗日乘子。
为是(1)的约束拉格朗日乘子。
为了求解问题(2),构造如下同伦方程:
 (3)
(3)
其中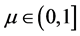 ,
, ,
,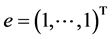 。我们作如下的假设:
。我们作如下的假设:
(C1)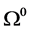 非空有界。
非空有界。
(C2) ,
, 是列满秩矩阵,其中
是列满秩矩阵,其中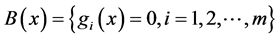 。
。
(C3) ( 在
在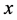 处的法锥条件)
处的法锥条件) ,
,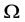 在
在 点的法锥与
点的法锥与 仅交于点
仅交于点 ,即
,即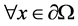 ,有
,有
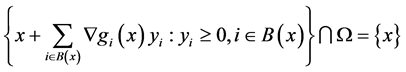 。
。
引理1 ,
, ,
, 为充分光滑函数,
为充分光滑函数, ,同伦方程如(3)定义,则对任意的
,同伦方程如(3)定义,则对任意的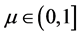 ,
, ,
, 是非奇异的。其中
是非奇异的。其中 。
。
证明:通过计算整理,有

其中 ,而
,而 为负对角矩阵,经过矩阵初等变换后,可得
为负对角矩阵,经过矩阵初等变换后,可得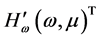 的相似阵
的相似阵

其中
 。
。
有
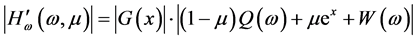 ,
,
因为 是充分光滑的凸函数,所以
是充分光滑的凸函数,所以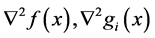 为半正定矩阵,又
为半正定矩阵,又 ,从而
,从而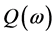 为半正定矩阵,因
为半正定矩阵,因 为正对角矩阵,通过计算知
为正对角矩阵,通过计算知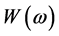 也为半正定矩阵,所以对任意的
也为半正定矩阵,所以对任意的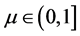 ,
, ,有
,有 为正定矩阵,
为正定矩阵, 。所以
。所以 ,即
,即 是非奇异矩阵。
是非奇异矩阵。
根据引理1及隐函数定理,对任意的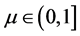 ,同伦方程(3)都有唯一的一个
,同伦方程(3)都有唯一的一个 与之对应。由点集
与之对应。由点集 构成
构成 内的连续曲线(其中
内的连续曲线(其中 ),即为组合同伦曲线。
),即为组合同伦曲线。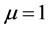 时
时 ,
, 时
时 ,
,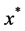 即为问题(1)的最优解。问题(1)的解可跟踪这条曲线得到。下面第2节构造的组合同伦牛顿算法就是跟踪这条曲线从而得到一系列迭代点:
即为问题(1)的最优解。问题(1)的解可跟踪这条曲线得到。下面第2节构造的组合同伦牛顿算法就是跟踪这条曲线从而得到一系列迭代点: ,且问题(1)的解就是其极限点
,且问题(1)的解就是其极限点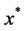 。第3节讨论了算法的收敛性。
。第3节讨论了算法的收敛性。
2. 算法
设组合同伦方程(3)的解曲线为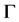 ,且当
,且当 时
时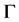 关于
关于 的分量是
的分量是 。由文献 [8] 、 [9] 知当
。由文献 [8] 、 [9] 知当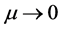 时,
时, 中关于
中关于 的极限点
的极限点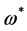 存在等价于问题(1)的K-K-T方程(2)有解
存在等价于问题(1)的K-K-T方程(2)有解 。
。
定义1:令
 ,
,
称 为
为 -锥邻域,其中
-锥邻域,其中 为邻域半径。
为邻域半径。
引理2:设 ,
,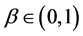 ,那么
,那么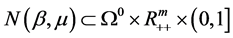 。
。
证:由于任意的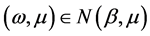 ,有
,有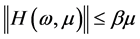 ,所以有
,所以有 。再由方程(3)的第二个等式有
。再由方程(3)的第二个等式有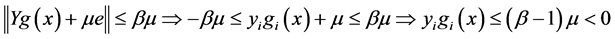 。
。
由已知 ,因此有
,因此有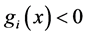 。综上所述有
。综上所述有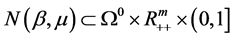 。
。
组合同伦牛顿算法
Step 0 (初始化)
令 ,
,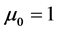 ,
, ,
,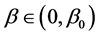 ,
, ,
,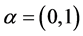 ,
, ,
,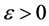 。
。
Step 1 (终止条件)
如果 ,则算法停止,且
,则算法停止,且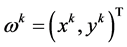 即为方程(3)的近似解。
即为方程(3)的近似解。
Step 2 (计算牛顿方向)
 (4)
(4)
其中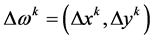 。
。
Step 3 (线搜索)
取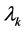 为
为 中的最大值,使之满足
中的最大值,使之满足
 (5)
(5)
令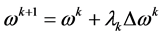 ,
, ,
,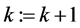 ,返回Step 1。
,返回Step 1。
3. 算法的全局收敛性
先讨论函数 以及算法的一些性质。
以及算法的一些性质。
引理3 [4] :假设 是由方程(3)定义的,给定有界凸集
是由方程(3)定义的,给定有界凸集 ,则对任意的
,则对任意的 ,
, ,存在常数
,存在常数 ,使得
,使得
 ,
, 。
。
定理1:算法是良定的。
证明:由引理1知,算法的Step 2良定。又由文献 [4] 知,当
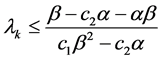
时,算法的Step 3良定,其中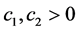 为常数。所以本文算法良定。
为常数。所以本文算法良定。
下面给出算法的全局收敛性。
定理2:设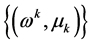 为由算法产生的无穷序列,则
为由算法产生的无穷序列,则
(i) 对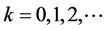
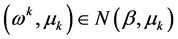 (6)
(6)
 (7)
(7)
(ii)序列 及
及 全局收敛于0。
全局收敛于0。
(iii) 存在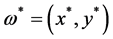 ,使得
,使得 。那么
。那么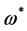 为同伦方程(3)的最优解,
为同伦方程(3)的最优解, 为问题(1)的最优解。
为问题(1)的最优解。
证明:
(i) 对 进行数学归纳法证明。
进行数学归纳法证明。
当 时,由算法知
时,由算法知 ,
,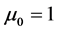 ,所以结论成立。假设对任意的
,所以结论成立。假设对任意的 有结论成立。那么对
有结论成立。那么对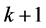 ,由算法可得到
,由算法可得到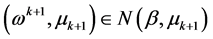 ,其中
,其中 ,且有
,且有
 ,所以(6) (7)式成立。
,所以(6) (7)式成立。
(ii)(1) 先证明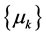 全局收敛于0。
全局收敛于0。
由定理1可知,对任意的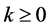 ,有
,有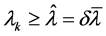 ,其中
,其中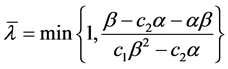 。结合(7)式可得
。结合(7)式可得 。故有
。故有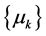 全局收敛于0。
全局收敛于0。
(2) 再证明 全局收敛于0。
全局收敛于0。
因为
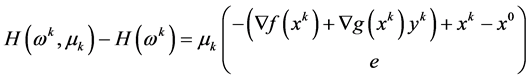 ,
,
所以必存在常数 ,使得
,使得 。根据前面所证,可得
。根据前面所证,可得
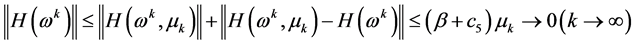
所以序列 全局收敛于0。
全局收敛于0。
(iii) 因为
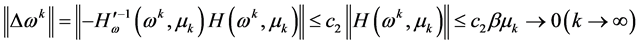 ,
,
因此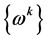 柯西收敛于某点
柯西收敛于某点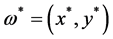 ,又从
,又从 可知
可知 。所以,
。所以,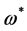 是同伦方程(3)的最优解,因而
是同伦方程(3)的最优解,因而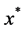 是问题(1)的最优解。
是问题(1)的最优解。
基金项目
广西高校科研项目(2013LX120),河池学院教改课题(2014EB019)。
文章引用
黄青群. 组合同伦法求不等式约束问题
Combined Homotopy Method for Inequality Constrained Problems[J]. 运筹与模糊学, 2016, 06(02): 60-65. http://dx.doi.org/10.12677/ORF.2016.62008
参考文献 (References)
- 1. Smale, S. (1976) A Convergent Process of Price Adjustment and Global Newton Method. Journal of Mathematical Economics, 3, 1-14. http://dx.doi.org/10.1016/0304-4068(76)90002-1
- 2. Kellogg, R.B., Li, T.Y. and Yorke, J.A. (1976) A Constructive Proof of the Brouwer Fixed-Point Theorem and Computational Results. SIAM Journal on Numerical Analysis, 18, 473-483. http://dx.doi.org/10.1137/0713041
- 3. 黄青群, 王祥玲, 杨萌. 凸非线性规划的一个预估–校正跟踪路径算法[J]. 广西科学, 2010, 17(2): 114-117.
- 4. 黄青群. 不等式约束优化问题的一个内点算法[J]. 河池学院学报, 2012, 32(5): 68-72.
- 5. 黄青群, 朱志斌, 卢钰松. 一般非线性规划的组合同伦牛顿法[J]. 湘潭大学自然科学学报, 2013, 35(1): 21-24.
- 6. 何非, 商玉凤, 梁心, 陶建武. 半内点同伦方法解均衡规划问题[J]. 吉林大学学报(理学版), 2014, 52(3): 470-474.
- 7. 赵雪, 杨月婷, 徐长玲. 多目标凸规划问题有效解集的求法[J]. 北华大学学报(自然科学版), 2015, 16(6): 701- 704.
- 8. Lin, Z., Li, Y. and Yu, B. (1996) A Combined HomotopyInterior Point Method for General Nonlinear Programming Problems. Applied Mathematics and Computation, 80, 209-224. http://dx.doi.org/10.1016/0096-3003(95)00295-2
- 9. Lin, Z., Yu, B. and Feng, G. (1997) A Combined HomotopyInterior Point Method for Convex Nonlinear Programming. Applied Mathematics and Computation, 84, 193-211. http://dx.doi.org/10.1016/S0096-3003(96)00086-0