Statistics and Application
Vol.05 No.03(2016), Article ID:18503,9
pages
10.12677/SA.2016.53024
The Parameter Estimation of the Mixture of Normal and Uniform Distribution Based on the Empirical Cumulative Distribution Function
Xiaoying Wang, Changlong Chen, Yinghua Li
School of Mathematics and Physics, North China Electric Power University, Beijing

Received: Aug. 20th, 2016; accepted: Sep. 4th, 2016; published: Sep. 9th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The normal mixture model is easily influenced by the outlier, and the maximum likelihood estimation of parameters is not robust estimation. Fraley and Raftery propose a normal model with the addition of a uniform distribution that is regarded as the outlier’s distribution. It fits the observation data accurately. The maximum likelihood function is unbounded when the two parameters are near infinitely, because of the probability density function of the uniform distribution. It is impracticable for using the EM algorithm directly. We can specify the parameters of uniform distribution with two different points in observation data which are fixed in the iteration. Then the parameters are specified by the estimation values whose maximum likelihood function is maximum. Coretto and Henning propose the gridding method, but this method also has large amount of calculation and low efficiency. Based on above, we propose a new method based on empirical cumulative distribution function for the general situation parameter estimation of the mixture of normal and uniform distribution, first estimating the parameter of the uniform distribution, second estimating the mixing proportion and the parameter of the normal distribution. We can know from the numerical simulation that our method has the advantages in high efficiency, high estimation precision, less amount of calculation and easy implementation.
Keywords:Empirical Cumulative Distribution Function, EM Algorithm, Mixture Model

基于经验累积分布的正态和均匀混合分布参数估计
王小英,陈常龙,李迎华
华北电力大学数理学院,北京

收稿日期:2016年8月20日;录用日期:2016年9月4日;发布日期:2016年9月9日

摘 要
混合正态分布模型易受离群点的影响,其参数的极大似然估计不是稳健估计。Fraley和Raftery在混合正态分布中添加一个均匀分布作为离群点的分布,能够准确的拟合观测数据,但是由于均匀分布概率密度函数的特殊性,即当两个参数充分接近时似然函数无界,因此直接利用EM算法进行迭代是行不通的。一般直接指定均匀分布的参数初始值为观测值中任意两个不同的数据点,在所有结果中选取最大似然函数值所对应的参数作为最终的参数估计值,尽管Coretto和Hennig提出网格化思想但是这种方法仍运算量大,效率低。针对一般情形的正态和均匀混合分布参数估计,本文提出了一种基于观测数据的经验累积分布函数的方法,直接估计均匀分布的参数,再估计混合比例和正态分布参数。数据模拟表明该方法具有效率高、计算量小、估计精度高且易于实现的优点。
关键词 :经验累积分布函数,EM算法,混合分布

1. 引言
混合分布模型一直是对复杂结构数据建模的最佳模型选择,因为混合分布模型不仅提供了一种用简单结构模拟复杂分布情形的模型,同时也为模拟同质性和异质性构建了一个自然框架。文献 [1] 中指出任意的密度函数都可以用混合正态分布模型拟合,即可以用混合分布模型拟合任意结构的数据,但是当混合模型的阶数较高时,由于模型的参数个数与阶数呈现近似倍数增加,故模型的参数估计更为复杂,所以应采用一种折中的方法来拟合复杂数据,即在模型阶数较低的前提下寻求拟合效果最好的模型。在混合分布模型中混合均匀分布一直作为一个特例,因为混合均匀分布不一定是可识别的,如文献 [2] 中举出的反例,当两个均匀分布的区间存在交叉时,模型的参数有可能是不可识别的,因此在考虑混合均匀分布的参数估计时应首先考虑参数的可识别性。均匀分布作为一种特殊的分布,常常被看作是异常值的分布,在混合分布中添加一个均匀分布作为观测数据中的异常值点的分布,使混合分布模型的拟合效果更好,模型能够更加准确的刻画出观测数据的内在规律和事物的本质特征。
文献 [3] 讨论了几种关于混合模型异常值点建模的方法,并比较几种方法的效果,在模型中添加异常值点的分布能够使参数估计是稳健估计。关于正态和均匀混合分布模型,Fraley和Raftery [4] 首次提出将一个均匀分布添加到混合正态分布中,并指定均匀分布的参数为整个观测数据的范围,即指定均匀分布的两个参数为观测数据的最小值和最大值;Dean和Raftery [5] 将同样的方法应用到生物中的微阵列数据。虽然这种方法能够拟合异常值点,但是这种指定均匀分布参数值的问题在实际应用中灵活性差,不能精确拟合观测数据中来自均匀分布的样本数据,另外Coretto [6] 指出这种情形下正态分布的参数估计不是稳健的。文献 [7] 证明了在似然函数非退化和模型可识别的前提下混合正态分布和均匀分布极大似然估计的存在性和一致性,并应用EM算法求解了单个均匀分布和正态分布混合的参数,但是最后参数估计结果严重依赖迭代的初始值,其本质是遍历整个观测数据而得到的,这样的做法耗时,且运算量大,虽然其后给出了网格化方法选取初始值,但运算量仍然大。
本文通过观测混合数据的经验累积分布函数发现正态分布的经验累积分布函数和均匀分布的经验累积分布函数有本质的区别,基于此我们可以利用观测数据的经验累积分布函数直接确定均匀分布的参数估计值,再通过EM算法迭代出正态分布参数和混合比例,经验累积分布函数和EM算法相结合的方法能够准确估计出混合正态分布和均匀分布的参数,不需要遍历整个数据集,并且当均匀分布的参数确定后,可以辅助EM算法选择合适的迭代初始值,从而能够降低因选取不合适的初始值而造成的迭代效果差的风险,使参数估计值更加准确。
本文的主要安排如下:第二节介绍混合正态分布和均匀分布模型数学表达式及问题;第三节介绍用经验累积分布函数确定均匀分布参数估计值的方法,并给出均匀分布参数估计的具体实现算法;第四节应用EM算法求解正态分布的参数和混合比例;第五节通过模拟10种不同结构的混合正态分布和均匀分布的数据来验证提出算法的估计准确性,并给出结论。
2. 模型介绍
混合正态分布和均匀分布的一般模型为
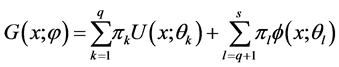 (2.1)
(2.1)
上式中的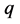 和
和 分别表示混合模型中的均匀分布和正态分布总体的个数,其中
分别表示混合模型中的均匀分布和正态分布总体的个数,其中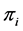 为第
为第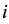 个分布所占的比重,
个分布所占的比重,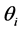 为第i个分布中所对应的参数。本文主要考虑
为第i个分布中所对应的参数。本文主要考虑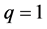 和
和 时的混合分布模型,则模型简化如下:
时的混合分布模型,则模型简化如下:
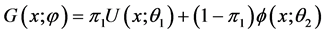 (2.2)
(2.2)
对于简化的模型(2.2)我们需要确定的参数为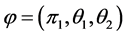 ,其中
,其中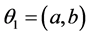 ,
,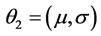 。传统的参数估计方法是直接应用极大似然估计,但是由于均匀分布的概率密度函数为区间长度的倒数,若直接应用极大似然估计,当均匀分布的两参数无限接近时,会使似然函数无界,导致极大似然估计不存在,对
。传统的参数估计方法是直接应用极大似然估计,但是由于均匀分布的概率密度函数为区间长度的倒数,若直接应用极大似然估计,当均匀分布的两参数无限接近时,会使似然函数无界,导致极大似然估计不存在,对
于正态分布当 时似然函数也无界。尽管Dennis [8] 提出在参数空间上添加限制
时似然函数也无界。尽管Dennis [8] 提出在参数空间上添加限制 的方法
的方法
(其中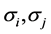 为分布所对应的标准差,
为分布所对应的标准差, ),但是这样使得在限制的参数空间上求极大似然估计过程更加困难。另外文献 [7] 在应用EM算法求极大似然估计的过程中,指定均匀分布的初始值后,每次迭代过程中均匀分布的参数估计值不变,因此这种方法需要遍历所有的观测数据为均匀分布的初始值,因此这种方法计算量大,且运算量随观测数据的规模指数增长,尽管其后来采用网格化的思想划分观测数据,但是这种方法的计算量仍然大,在大样本的情形下此方法不可行。本文提出的经验累积分布函数和EM算法相结合的方法能够极大地减小计算量,且不需要遍历整个数据集,提出的算法还能辅助EM算法选择合适的初始值。下面介绍本文如何应用经验累积分布函数估计均匀分布参数。
),但是这样使得在限制的参数空间上求极大似然估计过程更加困难。另外文献 [7] 在应用EM算法求极大似然估计的过程中,指定均匀分布的初始值后,每次迭代过程中均匀分布的参数估计值不变,因此这种方法需要遍历所有的观测数据为均匀分布的初始值,因此这种方法计算量大,且运算量随观测数据的规模指数增长,尽管其后来采用网格化的思想划分观测数据,但是这种方法的计算量仍然大,在大样本的情形下此方法不可行。本文提出的经验累积分布函数和EM算法相结合的方法能够极大地减小计算量,且不需要遍历整个数据集,提出的算法还能辅助EM算法选择合适的初始值。下面介绍本文如何应用经验累积分布函数估计均匀分布参数。
3. 经验累积分布函数估计均匀分布参数
3.1. 经验累积分布函数
经验累积分布函数(简称ecdf)在统计中有着非常重要的作用,其作为连接理论分布函数和实际数据分布的桥梁被广泛应用到实际数据分析中。设 为取自总体分布函数F(x)的观测数据,则其所对应的经验累积分布函数为:
为取自总体分布函数F(x)的观测数据,则其所对应的经验累积分布函数为:
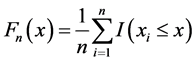 (3.1)
(3.1)
从经验累积分布函数的表达式可以看出其曲线呈现阶梯且逐渐上升。如果观测值 只有一个,
只有一个, 在
在 点的跃度为
点的跃度为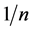 ;如果观测值
;如果观测值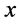 有
有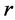 个,
个, 在
在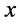 点的跃度为
点的跃度为 。理论分布函数与经验累积分布函数之间的对应关系为:
。理论分布函数与经验累积分布函数之间的对应关系为: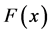 表示的是
表示的是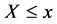 的概率,而经验累积分布函数表示的是在观测数据中小于或等于
的概率,而经验累积分布函数表示的是在观测数据中小于或等于 的数据所占的比例。文献 [9] 指出
的数据所占的比例。文献 [9] 指出 是
是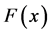 的无偏估计。文献 [10] [11] 讨论了经验累积分布函数的收敛性,并指出当样本量
的无偏估计。文献 [10] [11] 讨论了经验累积分布函数的收敛性,并指出当样本量 时,样本的经验累积分布函数
时,样本的经验累积分布函数 依概率收敛于总体
依概率收敛于总体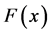 的分布函数,这就为我们利用样本数据推断总体的统计性质提供了理论依据。
的分布函数,这就为我们利用样本数据推断总体的统计性质提供了理论依据。
如图1为随机模拟的两种不同结构混合分布的经验累积分布函数,从图中可以明显的观察到混合分布中的均匀分布的经验累积分布函数的趋势近似一条直线,而正态分布的经验累积分布函数呈现抛物线形状,这与理论上的均匀分布和正态分布的经验累积分布函数一致,并且两者存在明显的分界点,通过确定分界点的位置,我们能够直接的确定均匀分布的参数。
3.2. 均匀分布参数估计
从图1中可以看出在均匀分布参数区间内其经验累积分布函数呈现近似直线,这与均匀分布理论上的累积分布函数的形状是一致的,因此我们可以用一条直接拟合经验累积分布函数如图2左图所示,但是用不同的区间段的经验累积分布函数值拟合出的直线是不一样的,对于如何选取合适的经验累积分布函数的数据段进行拟合,这里做出如下假设,假设总体的核密度估计的概率密度函数最高点落在均匀分布区间范围内。在上述假设的基础上我们可以通过核密度估计的方法确定选取拟合的区间段,下面给出估计均匀分布参数的具体算法流程:
1) 运用核密度估计的方法求观测数据的概率密度函数,假设最大概率密度所对应的观测数据点为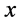 ;
;
2) 根据观测数据的密度选取合适的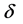 ,确定在区间
,确定在区间 内的观测数据集合
内的观测数据集合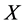 及其所对应的
及其所对应的
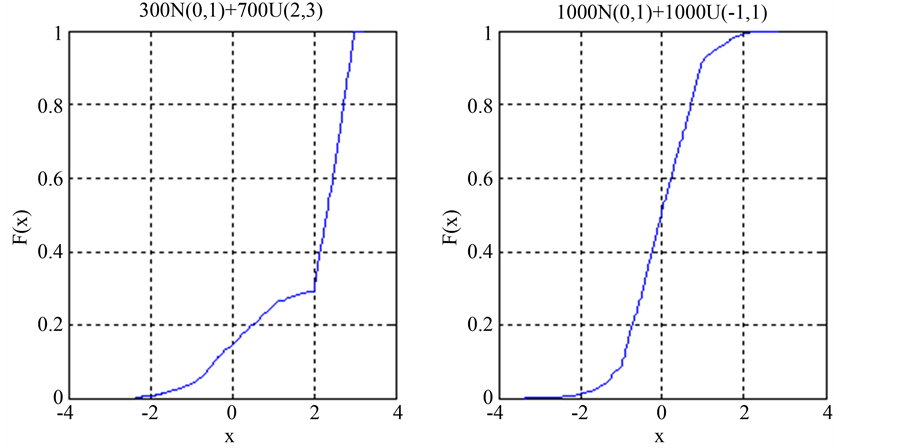
Figure 1. Empirical cumulative distribution function
图1. 经验累积分布函数
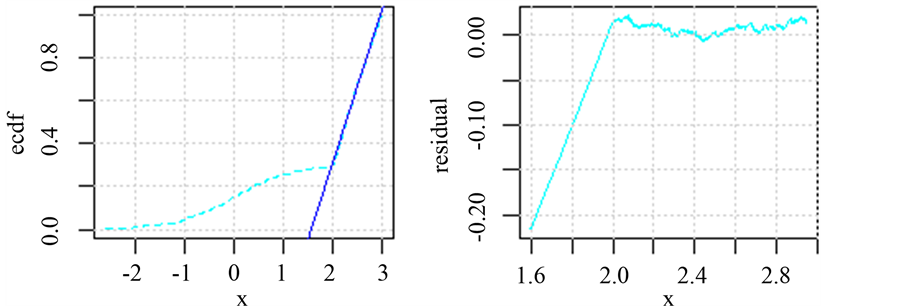
Figure 2. Fitting the empirical cumulative distribution function figure and the resident figure
图2. 拟合经验累积分布函数图及残差图
经验累积分布函数值集合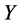 ;
;
3) 以集合 为自变量数据集,以集合
为自变量数据集,以集合 为因变量数据集进行线性回归;
为因变量数据集进行线性回归;
4) 截取回归直线,使其因变量的取值为 ,确定合适的容差
,确定合适的容差 ,选取经验累积分布函数和回归直线之间距离在容差
,选取经验累积分布函数和回归直线之间距离在容差 内的观测值,设其为集合
内的观测值,设其为集合 ;
;
5) 均匀分布的参数估计值分别为: 。
。
4. EM算法
自从Dempster [12] 提出EM算法之后,其因简单性和稳定性而被广泛应用到极大似然估计的计算中。在应用极大似然估计的文献中都能够看到EM算法的应用,文献 [13] 全面总结了EM算法及其各种扩展情形。本节主要介绍基于模型(2.2)的EM算法。
这里假设我们已经用第三节中的方法确定出均匀分布的参数值分别为 和
和 ,设
,设 ,
, 为指示函数,
为指示函数,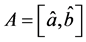 。则模型(2.2)可以写成
。则模型(2.2)可以写成
 (4.1)
(4.1)
此时需要用EM算法估计的参数为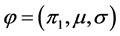 ,其所对应的对数似然函数为:
,其所对应的对数似然函数为:
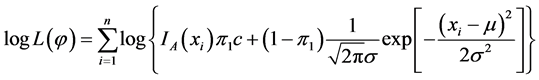 (4.2)
(4.2)
直接求解上式会很困难,采用经典的EM算法简化求解过程。EM算法的主要思想是在E步中利用完全数据的对数似然函数的条件期望近似不完全数据的对数似然函数,以达到简化不完全似然函数的目的,进而通过迭代的思想确定参数估计值(其中完全数据是指在观测数据中带有类标签的数据,表示为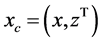 ,
,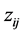 表示第
表示第 个观测值是否来自第
个观测值是否来自第 个分布,来自于第
个分布,来自于第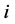 个总体记为1,否则记为0;而不完全数据指观测数据中没有类标签的数据,表示为x)。对于完全数据可以得到其对数似然函数为:
个总体记为1,否则记为0;而不完全数据指观测数据中没有类标签的数据,表示为x)。对于完全数据可以得到其对数似然函数为:
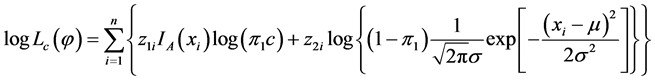 (4.3)
(4.3)
E步:求完全数据的对数似然函数的条件期望,对于给定的一个初始值 ,第
,第 次迭代中得到的对数似然函数近似值为:
次迭代中得到的对数似然函数近似值为:
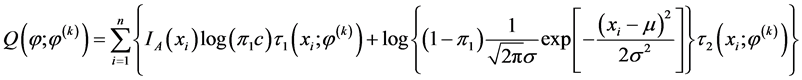 (4.4)
(4.4)
其中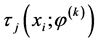 为后验概率可以通过
为后验概率可以通过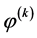 计算得到。
计算得到。
M步:最大化近似的对数似然函数,即最大化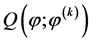 ,通过化简和计算可以得到第
,通过化简和计算可以得到第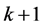 次迭代结果为
次迭代结果为
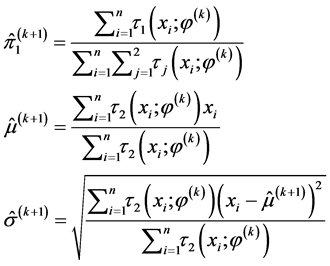 (4.5)
(4.5)
5. 数值模拟
5.1. 模拟数据产生
对混合分布模型的参数估计由于不同分布的比重、分布的交叠情形及样本量都直接影响最终的参数估计(这里的交叠指的是正态分布的均值是否在均匀分布的参数区间范围内),为了验证本文提出方法的试用情形,本文针对不同的混合比例、分布交叠情形和样本量共产生5大类10组模拟数据,每组组内由不同样本量的数据组成,因此总共有20种类型的模拟数据,对于每种模拟数据及其参数设置如表1所示。
5.2. 算法参数初始化
对于3.2节中的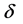 和
和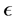 的选取,选取
的选取,选取 是为了保证有足够多的数据点做线性回归,可以根据数据的疏密程度进行适当的调整;
是为了保证有足够多的数据点做线性回归,可以根据数据的疏密程度进行适当的调整;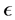 是衡量经验累积分布函数和选取特定点的线性回归直线之间的接近程度,
是衡量经验累积分布函数和选取特定点的线性回归直线之间的接近程度, 的选取直接决定了均匀分布的参数估计的准确性,另外
的选取直接决定了均匀分布的参数估计的准确性,另外 也受观测数据的稀疏程度及样本量的影响。本模拟中因为数据相对比较集中因此选取
也受观测数据的稀疏程度及样本量的影响。本模拟中因为数据相对比较集中因此选取 ,
,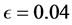 。
。
对于EM算法参数迭代的初始化问题,因为EM算法易受初始值的影响,选择一个好的初始值能使算法取得全局最优解,同样不好的初始值会使算法收敛到局部最优解。在考虑前面得到的均匀分布参数估计值较为准确的前提下,选取均匀分布的混合比例为观测值在均匀分布参数估计值区间内的比值,正态分布的均值和方差为不在均匀分布参数估计区间内的所有观测数据的均值和方差。
对于EM算法迭代的终止条件,主要从两个方面进行限制,一方面是迭代次数的限制,限定为300次,另一方面是对似然函数的限制,若两次迭代之间的似然函数的改变量小于最小预设精度,则停止迭代,模拟中选取的最小精度为0.001。
5.3. 参数估计模拟结果
对表1中的20种情形每种情形分别模拟100次,并计算估计值的均值和标准差见表2 (括号内为估
Table 1. The parameter setting of simulated data
表1. 模拟数据参数设置
计值的标准差)。
表2中的第三列和第四列分别对应着分布有交叠情形和无交叠情形下的参数估计,从中可以看出无交叠情形下的参数估计效果要优于有交叠情形下的参数估计效果,并且样本量的大小也直接影响估计效果,在模拟数据的参数设定相同的情况下,样本量为1000的估计效果要优于样本量为100的估计效果。
从表2第三列有交叠情形中可以看出其估计的混合比例较真值有很大的偏差,这是因为均匀分布和正态分布的数据完全的混合在一起,致使错误分类的比例增大;另外均匀分布的参数的估计受交叠程度的影响较大,在存在交叠的情形下,均匀分布参数估计会出现一定的误差,会低估均匀分布的参数;正态分布的参数受交叠情形影响较小,都能够准确的估计出参数值。
从表2第四列参数无交叠的情形中可以看出其估计效果易受样本量的影响,当样本量为1000时,其估计效果明显,因为两分布参数无交叠,所以在应用3.2节中的算法估计均匀分布参数时能够准确定位出均匀分布的位置,同时也为EM算法选定准确的初始值,因此混合比例和正态分布的参数估计值也较有交叠的情形下准确。
考虑表2的模拟结果,本文提出的参数估计方法对两个分布无交叠情形的效果要优于有交叠的情形,特别是无交叠的情形只要样本量足够大,此方法能较为准确的估计出参数值;对于3.2节中提出的估计
Table 2. The parameter estimation of simulation data
表2. 模拟数据的参数估计
均匀分布参数的方法,理论上均匀分布的累积分布函数为一条倾斜的直线,只要实际数据中的均匀分布的经验累积分布函数呈现一条倾斜的直线,其经验累积分布函数就能够用线性回归的方法确定,进而估计出均匀分布的参数;应用3.2节提出的算法不仅能够直接准确的估计出均匀分布的参数还能够为EM算法迭代提供选择初始值的依据;另外本文提出的算法在EM算法之前就直接确定均匀分布的参数,不需要遍历整个数据集。
6. 结论
本文提出的基于经验累积分布函数的方法估计均匀分布参数充分利用了均匀分布的累积分布函数的性质,只要均匀分布占一定的比重和数据样本量足够多,就能够用线性回归的方法确定均匀分布的参数值,且估计的精度高,与EM算法结合估计混合正态分布和均匀分布的参数值。并且该算法具有运算量小、效率高、实现简单等优点。
文章引用
王小英,陈常龙,李迎华. 基于经验累积分布的正态和均匀混合分布参数估计
The Parameter Estimation of the Mixture of Normal and Uniform Distribution Based on the Empirical Cumulative Distribution Function[J]. 统计学与应用, 2016, 05(03): 237-245. http://dx.doi.org/10.12677/SA.2016.53024
参考文献 (References)
- 1. McLachlan, G. and Peel, D. (2004) Finite Mixture Models. John Wiley & Sons, New York, 11-14.
- 2. 谭鲜明. 有限正态混合模型的参数估计及应用[D]: [博士学位论文]. 天津: 南开大学, 2002.
- 3. Coretto, P. and Hennig, C. (2010) A Simulation Study to Compare Robust Clustering Methods Based on Mixtures. Advances in Data Analysis and Classification, 4, 111-135. http://dx.doi.org/10.1007/s11634-010-0065-4
- 4. Fraley, C. and Raftery, A.E. (1998) How Many Clusters? Which Clustering Method? Answers via Model-Based Cluster Analysis. The Computer Journal, 41, 578-588. http://dx.doi.org/10.1093/comjnl/41.8.578
- 5. Dean, N. and Raftery, A.E. (2005) Normal Uniform Mixture Differential Gene Expression Detection for cDNA Microarrays. BMC Bioinformatics, 6, 1. http://dx.doi.org/10.1186/1471-2105-6-173
- 6. Coretto, P. (2008) The Noise Component in Model-Based Clustering. Ph.D. Thesis, University of London, London.
- 7. Coretto, P. and Hen-nig, C. (2011) Maximum Likelihood Estimation of Heterogeneous Mixtures of Gaussian and Uniform Distributions. Journal of Statis-tical Planning and Inference, 141, 462-473. http://dx.doi.org/10.1016/j.jspi.2010.06.024
- 8. Dennis Jr., J.E. (1981) Algorithms for Nonlinear Fitting. Cambridge University Press, England.
- 9. Rice, J. (2006) Mathematical Statistics and Data Analysis. Nelson Education, Australia, 378-380.
- 10. 王豹. 浅谈经验分布函数的收敛性[J]. 徐州教育学院学报, 2008, 23(3): 80-81.
- 11. 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 第二版. 北京: 高等教育出版社, 2006: 37-43.
- 12. Dempster, A.P., Laird, N.M. and Rubin, D.B. (1977) Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society, Series B (Methodological), 39, 1-38.
- 13. McLachlan, G. and Krishnan, T. (2007) The EM Algorithm and Extensions. 2nd Edition, John Wiley & Sons, New York.
